Continuous Autoregressive Language Models

Paper Translate

목록 보기

7/7

Author: Chenze Shao, Darren Li, Fandong Meng, Jie Zhou
Affilation: Tencent Inc, Tsinghua University
Venue: arXiv
Comments:
Date: October 2025
Paper Link: https://arxiv.org/abs/2510.27688

⭐️ Key Takeaways
1. CALM(Continuous Autoregressive Language Models)은 LLM의 비효율적인 토큰별 생성 패러다임을 극복하기 위해, K개 토큰 덩어리를 단일 연속 벡터로 압축하여 예측하는 방식으로 전환함으로써 각 생성 단계의 의미적 대역폭을 확장한다.
2. CALM 프레임워크는 각 자기회귀 단계의 의미적 대역폭을 확장하는 것이 언어 모델의 성능-계산 경계선을 미는 강력한 새로운 확장 축임을 강조하며, 우수한 성능-계산 상충 관계를 달성한다.
3. 명시적인 우도 계산이 불가능한 연속 도메인에서의 훈련, 평가, 제어 가능한 표집을 가능하게 하기 위해, CALM은 에너지 손실, BrierLM 평가 메트릭, 그리고 우도 비의존적 온도 표집 알고리즘을 포함하는 포괄적인 우도 비의존적 도구 키트를 개발했다.

Abstract

대규모 언어 모델(LLMs)의 효율성은 근본적으로 순차적인 토큰별 생성 프로세스에 의해 제한된다. 우리는 이 병목 현상을 극복하기 위해 LLM 스케일링을 위한 새로운 설계 축, 즉 각 생성 단계의 의미론적 대역폭을 증가시키는 것이 필요하다고 주장한다. 이를 위해, 우리는 이산적인 다음 토큰 예측에서 연속적인 다음 벡터 예측으로의 패러다임 전환인 CALM(Continuous Autoregressive Language Models)을 소개한다. CALM은 높은 충실도의 오토인코더를 사용하여 K개의 토큰 청크를 단일 연속 벡터로 압축하며, 이 벡터로부터 원래 토큰을 99.9% 이상의 정확도로 재구성할 수 있다. 이를 통해 우리는 언어를 이산 토큰 대신 연속 벡터의 시퀀스로 모델링할 수 있으며, 이는 생성 단계의 수를 K배 감소시킨다. 이러한 패러다임 전환은 새로운 모델링 툴킷을 필요로 하므로, 우리는 연속 도메인에서 강건한 학습, 평가 및 제어 가능한 샘플링을 가능하게 하는 포괄적인 우도(likelihood) 비의존적 프레임워크를 개발한다. 실험 결과, CALM은 성능-계산 트레이드오프를 크게 개선하여, 강력한 이산형 기준선(discrete baselines)과 유사한 성능을 훨씬 낮은 계산 비용으로 달성한다. 더 중요하게는, 이러한 발견들은 다음 벡터 예측을 초고효율 언어 모델로 나아가는 강력하고 확장 가능한 경로로 확립한다.

1. Introduction

대규모 언어 모델(LLMs)은 인간 언어를 이해하고, 생성하며, 추론하는 데 있어 전례 없는 능력을 입증하며 인공지능 분야에 혁명을 일으켰다. 그러나 이 놀라운 성공은 중대한 도전 과제, 즉 그들의 막대한 계산 요구 사항이라는 그림자에 가려져 있다. 최첨단 LLM의 훈련 및 추론은 막대한 계산 자원을 필요로 하며, 이는 엄청난 비용과 심각한 환경 문제로 이어진다. 이러한 비효율성의 핵심에는 이 모델들의 근본적인 패러다임, 즉 이산적인 토큰 시퀀스에서 작동하는 자기회귀 생성 프로세스가 자리 잡고 있다. 계산 비용이 시퀀스 길이에 비례하여 증가하기 때문에, 장문의 텍스트를 생성하거나 광범위한 컨텍스트를 처리하는 것은 여전히 근본적인 병목 현상으로 남아 있으며, 이러한 강력한 모델의 확장성과 접근성을 제한한다.

이제 LLM에서 보편적으로 사용되는 이산 토큰은 초기 모델링 패러다임으로부터의 중추적인 진화의 결과이다. 초기에, 문자 수준에서 작동하던 모델은 극도로 긴 시퀀스의 계산 부담으로 인해 어려움을 겪었다. 이후 현대적인 서브워드 토큰화(subword tokenization)로의 전환은 각 텍스트 단위의 정보 밀도를 높이는 것이 시퀀스 길이를 줄이고 모델 효율성을 극적으로 향상시킨다는 중요한 통찰력에 의해 추진되었다. 이러한 역사적 성공은 다음 단계의 효율성을 달성하기 위한 명확한 경로를 제시한다: 각 예측 단위의 의미론적 대역폭을 계속해서 증가시키는 것이다.

그러나 우리는 이러한 경로가 이산적 표현의 본질적인 제약으로 인해 근본적인 한계에 도달했다고 주장한다. 현대 LLM의 일반적인 어휘집은 약 32,000개에서 256,000개의 항목에 이르지만, 각 토큰은 놀라울 정도로 적은 양의 정보, 즉 단지 15비트에서 18비트만을 전달한다(예: $\log_2(32768) = 15$ ). 예를 들어, 전체 구문(phrase)을 표현하기 위해 이 용량을 증가시키려면 어휘집 크기가 기하급수적으로 증가해야 하며, 이는 이 어휘집에 대한 최종 소프트맥스(softmax) 계산을 감당할 수 없는 병목 현상으로 만들 수 있다. 이는 이산 토큰의 정보 밀도가 확장 가능하지 않다는 중대한 한계를 드러낸다. 결과적으로, 심각한 불일치가 발생했다. 모델 용량은 전례 없는 수준으로 확장되었지만, 한 번에 낮은 정보의 이산 단위를 예측하는 작업 자체는 진화하지 않았다. 우리는 이제 그 처리량(throughput)을 근본적으로 제한하는 작업에 막대한 표현력을 가진 모델을 배치하고 있으며, 이는 모델이 단순하고 정보량이 적은 토큰을 하나씩 힘들게 예측하도록 강제한다.
본 연구에서, 우리는 이산 토큰에서 연속 도메인 표현으로의 패러다임 전환을 도입함으로써 이러한 한계에 직접적으로 맞선다. 우리 접근 방식의 핵심은 K개의 토큰 덩어리를 단일의 밀집된 연속 벡터로 압축하고, 결정적으로 이 벡터로부터 원래 토큰을 높은 충실도로 재구성하도록 훈련된 오토인코더이다. 정보 밀도를 높이기 위해 어휘집 크기의 기하급수적인 증가를 요구하는 이산 패러다임과 달리, 우리의 연속 표현은 확장 가능한 경로를 제공한다. 즉, 더 큰 K를 수용하기 위해 벡터의 차원(dimensionality)을 늘리는 것만으로 벡터의 정보 용량을 자연스럽게 확장할 수 있다. 이 설계는 자기회귀 단계의 수를 K배 감소시킨다. 궁극적으로, 이는 언어 모델링을 이산 토큰 시퀀스에 대한 다음 토큰 예측 작업에서 연속 벡터 시퀀스에 대한 다음 벡터 예측 작업으로 재구성할 수 있게 하며, 이는 그림 1에 개념적으로 설명되어 있다.

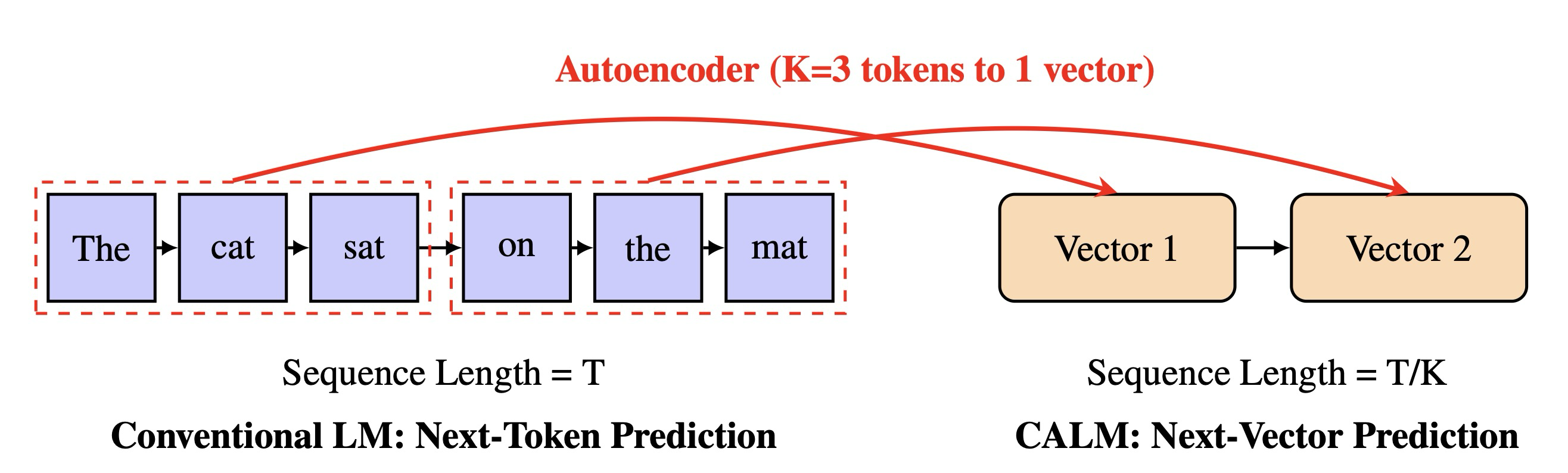
Figure 1: Comparison between conventional token-by-token generation and our proposed vector-by-vector framework (CALM)

그러나 연속 도메인으로의 전환은 중대한 도전 과제를 야기한다. 유한한 어휘집이 없기 때문에, 모델은 표준 소프트맥스 레이어를 사용하여 모든 가능한 결과에 대한 명시적인 확률 분포를 계산할 수 없다. 이를 해결하기 위해, 우리는 연속 자기회귀 언어 모델(CALM)을 위한 포괄적인 우도(likelihood) 비의존적 프레임워크를 개발한다. 본 논문의 나머지 부분을 구성하는 우리의 주요 기여는 다음과 같다:

강력하고 경량화된 오토인코더 (2절): 우리는 먼저 강건한 벡터 표현을 생성하도록 설계된 효율적인 오토인코더 아키텍처를 소개한다. 우리는 이 모델이 소형이면서도 강력할 수 있으며, 다운스트림 언어 모델링 작업을 위한 전제 조건인 원본 토큰의 높은 충실도 재구성을 보장함을 입증한다.
Likelihood 비의존적 언어 모델링 (3절): 연속 벡터 공간에서 생성 모델링을 수행하기 위해, 우리는 마지막 은닉 상태에 조건을 부여하여 출력 벡터를 생성하는 경량화된 생성 헤드(generative head)를 사용한다. 생성 헤드는 모든 연속 생성 모델이 될 수 있지만, Diffusion 또는 Flow Matching과 같은 옵션은 반복적인 샘플링 프로세스에 의존하여 심각한 추론 병목 현상을 재도입한다. 따라서 우리의 프레임워크는 효율적인 단일 단계 연속 벡터 생성을 위해 설계된 최신 아키텍처인 에너지 트랜스포머(Energy Transformer)를 특별히 채택하며, 경험적으로 우수한 생성 품질을 입증한다.
Likelihood 비의존적 LM 평가 (4절): 시적인 우도가 없기 때문에 퍼플렉서티(Perplexity)와 같은 전통적인 메트릭은 적용할 수 없다. 우리는 이를 해결하기 위해 브라이어 점수(Brier score)를 기반으로 한 새로운 언어 모델링 메트릭인 BrierLM을 제안한다. BrierLM이 엄격하게 적절(strictly proper)함을 보여주며, 이는 모델 능력의 공정한 비교를 이론적으로 보장한다. 결정적으로, BrierLM은 모델에서 샘플을 추출하는 것만으로 불편향적으로 추정될 수 있으므로, 우도를 다루기 어려운 CALM에 완벽하게 적합하다.
Likelihood 비의존적 Temperature 샘플링 (5절): 온도 샘플링을 통한 제어된 생성은 최신 LLM의 필수적인 기능이지만, 이는 확률 분포의 명시적인 조작에 의존한다. 우리는 이론적으로 정확한 온도 분포에서 샘플을 추출할 수 있는 원칙적인 우도 비의존적 샘플링 알고리즘을 소개하고, 매우 효율적인 배치 근사치(batch approximation)를 함께 제시한다.

우리는 표준 언어 모델링 벤치마크에서 CALM 프레임워크를 경험적으로 검증하며, 이는 우수한 성능-계산 트레이드오프를 입증한다. 예를 들어, K=4 토큰을 그룹화하는 CALM은 강력한 이산형 기준선(discrete baselines)과 유사한 성능을 훨씬 낮은 계산 비용으로 제공한다. 이러한 발견은 언어 모델을 위한 새로운 설계 축을 강조한다. 즉, 성능을 위해 단순히 매개변수와 데이터만 확장하는 대신, 이제 각 단계의 정보 용량을 계산 효율성을 위한 강력한 새로운 지렛대(lever)로 확장할 수 있다.

2. Autoencoder

2.1 High-Fidelity Reconstruction

CALM 프레임워크의 근본적인 구성 요소는 $K$ 개의 이산 토큰 덩어리와 하나의 연속 벡터 사이의 전단사(bijective) 매핑을 학습하는 임무를 맡은 오토인코더이다. 형식적으로, 우리는 인코더 $f_{enc}:V^K \rightarrow \mathbb{R}^l$ 와 디코더 $g_{dec}:\mathbb{R}^l \rightarrow V^K$ 를 탐색하며, 여기서 $V$ 는 vocab을 나타낸다. 주어진 토큰 시퀀스 $\bold{x}_{1:K}=(x_1, …, x_K)$ 에 대해, 재구성된 $g_{dec}(f_{enc}(\bold{x}_{1:K}))$ 가 $\bold{x}_{1:K}$ 에 가깝게 근사하는 것을 목표로 한다. 단순성과 계산 효율성을 위해, 우리는 오토인코더를 문맥 독립적(context-free)으로 설계하며, 이는 오토인코더가 주변 시퀀스와 독립적으로 각 토큰 덩어리를 처리함을 의미한다. 이전 벡터 표현에 조건화하는 문맥 인식(context-aware) 오토인코더는 자연스럽고 유망한 다음 단계이지만, 이는 향후 탐구를 위해 남겨둔다.

인코더는 입력 시퀀스 $\bold{x}_{1:K}$ 를 $K$ 개의 임베딩으로 매핑하는 것으로 시작한다. 각 임베딩은 위치별 피드 포워드 네트워크(FFN)에 의해 독립적으로 처리된다. 그 결과로 생성된 $K$ 개의 은닉 상태는 linear layer를 통해 flattened되고 압축된다: $\mathbb{R}^{Kd} \rightarrow \mathbb{R}^d$ . 이 통일된 표현은 두 번째 FFN과 linear projection을 거쳐 $l$ -차원의 잠재 벡터 $z$ 를 생성한다.

디코더 아키텍처는 인코더를 모방한다. 디코더는 먼저 선형 계층과 FFN을 사용하여 $z$ 를 변환하여 $d$ -차원의 은닉 상태를 얻으며, 이 상태는 또 다른 선형 계층에 의해 $Kd$ 차원으로 호가장되고 $K$ 개의 은닉 상태 시퀀스로 재구성된다. 이 상태들 각각은 두 번째 FFN을 거친 다음, 가중치가 묶인(tied) 입력 임베딩 행렬을 사용하여 어휘 로짓(vocabulary logits)으로 투영된다. 최종적으로, 토큰들은 이러한 로짓에 argmax 연산을 적용하여 재구성한다.

오토인코더는 $K$ 개의 모든 토큰 위치에 걸쳐 표준 교차 엔트로피 손실을 최적화함으로써 재구성 오류를 최소화하도록 훈련된다:

L_{ae}(\bold{x}_{1:K}=-\sum^K_{i=1}\log p_{dec}(x_i \mid \bold{z}=f_{enc}(\bold{x}_{1:K}))~~~~(1)

우리는 이 아키텍처를 경험적으로 검증하며, 이는 매우 효과적이고 효율적임을 발견한다. 예를 들어, $K=4$ 개의 토큰을 그룹화할 때, 단지 $l=10$ 차원의 latent 벡터만으로도 99.9% 이상의 토큰 수준 정확도로 높은 충실도의 재구성을 달성하기에 충분하다. 더욱이, 이 오토인코더는 예외적으로 경량화되어 있으며, 얕은 아키텍처와 $d=512$ 의 적당한 은닉 차원을 사용하여, 그 계산 오버헤드는 언어 모델의 오버헤드에 비해 거의 무시할 수 있는 수준이다.

2.2 Robust Vector Representation

위에 기술된 오토인코더는 거의 완벽한 재구성을 달성하지만, 우리는 이 오토인코더가 생성하는 벡터 공간을 기반으로 연속 언어 모델을 효과적으로 훈련하는 것은 실제적으로 불가능하다는 것을 발견했다. 이 문제의 근본적인 원인은 재구성을 위해서만 최적화된 오토인코더가 예외적으로 취약한 표현을 학습한다는 점이다. 매끄러운 잠재 다양체(smooth latent manifold)를 형성해야 할 동기가 없기 때문에, 인코더는 정보를 최대 효율로 압축하도록 학습하며, 이는 극도로 불규칙한 매핑을 생성한다. 이러한 공간에서 잠재 벡터 $z$ 에 작은 교란(perturbation) — (예를 들어, 생성 모델이 만드는 피할 수 없는 작은 오류) — 이 발생하면, 디코더가 완전히 관련 없는 토큰 시퀀스를 재구성하게 만들 수 있다. 따라서, 우리의 CALM 프레임워크가 실현 가능하려면, 오토인코더는 또 다른 중요한 목표를 충족해야 한다: 그 벡터 표현은 강건(robust)해야 한다.

Variational Regularization. 강건한 잠재 공간을 구축하기 위한 우리의 주된 전략은 결정론적 오토인코더에서 변이형 오토인코더(variational autoencoder, VAE)로 전환하여 잠재 다양체를 매끄럽게 만드는 것이다. 이는 매끄럽고 구조화된 잠재 공간 내에서 작동하는 저명한 생성 모델들과 접근 방식을 일치시킨다. 입력 청크를 벡터 $z$ 로 직접 매핑하는 대신, 인코더는 이제 대각 가우시안 분포의 매개변수 $\mu$ 와 $\sigma$ 를 출력하며, 잠재 벡터는 여기서 샘플링된다: $\bold{z} \sim N(\mu, \sigma^2 \bold{I})$ . 이러한 변화에는 인코딩된 분포가 표준 정규 사전(prior) $N(0, \bold{I})$ 에서 벗어나는 것을 페널티화하는 새로운 목적 함수 항인 KL divergence 손실이 수반된다. 따라서 전체 손실 함수는 재구성 손실 $L_{ae}$ 와 정규화 항 $L_{KL}$ 의 가중합이 된다:

L_{\text{total}}=L_{ae} + \beta \cdot L_{KL}, ~~~~(2)

여기서 $\beta$ 는 두 목적 사이의 균형을 맞추는 하이퍼파라미터이며 (우리는 $\beta=0.001$ 로 설정한다), $L_{KL}$ 은 KL 발산으로 다음과 같이 정의된다:

L_{KL}(p_E(\bold{z} \mid \bold{x}_{1:K}) \mid \mid N(0,\bold{I})) = -\frac{1}{2} \sum^l_{i=1}(1+\log{\sigma^2_i}-\sigma^2_i - \mu^2_i). ~~~~(3)

이 변이형 목적 함수는 인코더가 z 내의 임의로 정밀하거나 큰 규모의 값에 의존하는 것을 억제하여, 생성 모델링에 더 적합한 더 매끄럽고 정규화된 잠재 다양체를 촉진한다.

Preventing Posterior Collapse. VAE 훈련에서 중요한 도전 과제는 사후 붕괴(posterior collapse)이다. 이 문제는 우리 모델에서 일부 잠재 차원이 표준 정규 사전으로 완전히 붕괴되는 경향으로 나타났다. 차원을 붕괴시키면 KL 발산이 0으로 가지만, 그 차원은 재구성에 대해 정보를 제공하지 못하게 된다. 더 중요하게는, 이러한 순수한 노이즈 차원이 다운스트림 언어 모델의 훈련을 방해하는 혼란스러운 신호를 도입하여 학습 과정을 불안정하게 만든다. 이를 완화하기 위해, 우리는 Kingma et al. (2016)의 KL 클리핑 전략을 채택하며, 이는 각 차원의 KL 손실을 상수 하한(floor)에서 클리핑하여 목적 함수를 수정한다:

L^{clip}_{KL}=\sum^l_{i=1}\max(\lambda_{KL}, L_{KL, i}),~~~~(4)

여기서 $L_{KL, i}$ 는 $i$ 번째 차원에 대한 KL 발산이고 $\lambda_{KL}$ 은 임계값이다 (우리는 0.5를 사용한다). 이 기술은 모든 차원이 재구성에 적극적으로 참여하도록 장려하여 붕괴를 방지하고 밀집되고 구조화된 표현을 조성한다.

Dropout for Enhanced Robustness. 변이형 방법을 통해 잠재 공간을 구조화하는 것 외에도, 우리는 훈련 중에 두 가지 상호 보완적인 형태의 드롭아웃을 사용하여 노이즈를 주입함으로써 강건성을 더욱 향상시킨다. 첫째로, 잠재 벡터 $\bold{z}$ 가 디코더로 전달되기 전에 $p=0.15$ 의 비율로 드롭아웃을 적용한다. 이는 오토인코더가 잉여 표현(redundant representation)을 학습하도록 강제하여, 다운스트림 생성 모델의 사소한 예측 오류에 강건하게 만든다. 둘째로, 입력 토큰의 일부( $p=0.15$ )를 무작위로 마스킹하여 드롭아웃을 적용한다. 이는 CBOW(Continuous Bag-of-Words) 방법(Mikolov et al., 2013)과 유사하게, 오토인코더가 그 문맥으로부터 마스킹된 토큰을 추론하도록 강제하며, 단순한 토큰-인덱스 압축을 수행하는 대신 잠재 벡터를 덩어리의 의미적 문맥으로 풍부하게 만든다. 중요하게도, 이러한 드롭아웃 기술은 강건한 잠재 표현을 구축하기 위해 오토인코더의 훈련 단계에서만 독점적으로 사용되며, 이후의 연속 언어 모델 훈련 및 추론 중에는 비활성화된다.

이러한 기술들의 통합은 강력하고 강건한 오토인코더를 생성한다. $K=4$ 의 토큰 덩어리의 경우, 우리는 이제 정보를 잉여적으로 인코딩하는 데 필요한 용량을 제공하는 $l=128$ 차원의 잠재 벡터를 사용한다. 인코더는 표준 편차 $\sigma_i$ 가 0.3으로 수렴하는 사후 분포를 학습한다. 이는 잠재 벡터 $\bold{z}$ 를 샘플링하는 것이 예측된 평균 $\bold{\mu}$ 를 상당한 가우시안 노이즈 $\bold{\sigma} \approx 0.3 \bold{I}$ 로 효과적으로 교란(Perturbate)함을 의미한다. 이러한 상당한 잠재적 교란에도 불구하고, 디코더는 여전히 99.9%를 초과하는 토큰 수준 정확도를 유지한다. 높은 충실도와 높은 강건성을 결합한 이 벡터 표현은 이후의 연속 자기회귀 언어 모델(CALM) 학습을 위한 견고한 토대를 마련한다.

3. Likelihood-Free Language Modeling

3.1 Next-Vector Prediction

2절에서 개발된 오토인코더는 $K$ 개의 이산 토큰 덩어리와 하나의 연속 벡터 사이에 강건하고 높은 충실도의 매핑을 확립한다. 이 매핑을 통해 우리는 언어 모델링을 이산 토큰 시퀀스에 대한 다음 토큰 예측 작업에서 연속 벡터 시퀀스에 대한 다음 벡터 예측 작업으로 재구성할 수 있다. 구체적으로, $T$ 개의 토큰으로 구성된 시퀀스 $\bold{X}=(x_1, ..., x_T)$ 는 먼저 $L=T/K$ 개의 겹치지 않는 덩어리로 그룹화된다. 그런 다음, 인코더 $f_{enc}$ 는 원래 시퀀스를 더욱 압축된 새로운 연속 벡터 시퀀스로 변환한다:

\bold{Z}=(\bold{z}_1, \bold{z}_2, ..., \bold{z}_L), ~~~~\text{where}~~~~\bold{z}_i=f_{enc}(x_{(i-1)K+1}, ..., x_{iK}). ~~~~(5)

결과적으로, 자기회귀 목표는 시퀀스에서 다음 벡터를 예측하는 것으로 진화한다:

p(\bold{Z})= \prod^L_{i=1}p(\bold{z}_i \mid \bold{z}_{<i}). ~~~~(6)

이러한 자기회귀 구조는 보존되지만, 다음 요소를 예측하는 기본 메커니즘은 재설계되어야 한다. 유한한 어휘집에 대한 확률 분포를 계산하기 위해 소프트맥스 계층에 의존하는 표준 언어 모델과 달리, 우리의 모델은 무한한 공간 $\mathbb{R}^l$ 내의 벡터를 예측해야 한다. 소프트맥스 함수는 이러한 셀 수 없는 집합에 적용할 수 없으며, 따라서 명시적인 확률 밀도 $p(\bold{z}_i \mid \bold{z}_{<i})$ 는 다루기 어렵게 된다. 이는 다음과 같은 두 가지 중요한 도전을 야기한다:

Training: 우도 $p(\bold{z}_i \mid \bold{z}_{<i})$ 를 계산할 수 없게 되어, 훈련에 최대 우도 추정(즉, 교차 엔트로피 손실 최소화)을 사용할 수 없게 된다.
Evaluation: 모델의 우도에서 직접 파생되는 퍼플렉서티와 같은 표준 평가 메트릭은 더 이상 모델 성능을 측정하는 데 사용될 수 없다.

우리는 이 두 가지 도전에 대해 차례로 다룬다. 훈련 문제의 경우, 본 섹션의 나머지 부분에서 우도 비의존적 언어 모델링(likelihood-free language modeling)에 대한 우리의 접근 방식을 소개하며, 평가 문제의 경우, 4절에서 우도 비의존적 평가 방법론을 제안한다.

3.2 Generative Head

연속 데이터에 대한 생성 모델링은 이미지 및 오디오 합성(synthesis)과 같이 데이터가 본질적으로 연속적인 영역의 기초로서 확립된 분야이다. 최근의 유망한 패러다임은 이러한 접근 방식들을 자기회귀 모델과 결합한다: 트랜스포머 백본(Transformer backbone)은 조건화 은닉 상태를 예측하며, 이 상태는 후속 생성 모델에 의해 각 단계의 연속적인 출력을 생성하는 데 사용된다. 우리의 연속 자기회귀 언어 모델(CALM)은 이 패러다임을 채택하지만, 이 생성 구성 요소의 설계를 제약하는 계산 효율성에 대한 중요한 초점을 맞춘다. 따라서 우리는 이 구성 요소를 경량 생성 헤드로 개념화한다. 공식적으로, 생성 헤드는 트랜스포머의 은닉 상태 $\bold{h}_{i-1} \in \mathbb{R}^d$ 를 받아 조건부 분포에서 샘플 $\bold{z}_i \in \mathbb{R}^l$ 을 추출하는 확률적 함수이다:

\bold{h}_{i-1} = \text{Transformer}(\bold{z}_{1:i-1}), ~~~~ \bold{z}_i \sim p(\cdot \mid \bold{h}_{i-1}). ~~~~(7)

생성 헤드는 어떤 연속 생성 모델이든 될 수 있지만, Diffusion 또는 Flow Matching 과 같은 저명한 옵션들은 반복적인 샘플링 프로세스에 의존하는데, 이는 단일 벡터를 생성하기 위해 수십 또는 수백 번의 네트워크 평가를 필요로 한다. 이로 인해 자기회귀 단계 수를 줄여 얻은 속도 향상을 직접적으로 상쇄하는 심각한 추론 병목 현상이 재도입된다. 따라서 CALM 아키텍처는 고품질의 단일 단계 생성이 가능한 생성 헤드를 요구하며, 우리는 이 문제를 에너지 기반 목적 함수(energy-based objective)를 통해 다음 절에서 해결한다.

3.3 Energy Transformer

3.3.1 Strictly Proper Scoring Rules

고품질의 단일 단계 생성이 가능한 생성 헤드에 대한 요구를 충족하기 위해, 우리는 생성 작업을 엄격하게 적절한 점수 규칙(strictly proper scoring rules)의 최적화로 구성하는 Shao et al. (2024; 2025b)의 연구에서 영감을 얻는다. 형식적으로, 점수 규칙 $S(P, y)$ 는 결과 $y$ 를 관찰했을 때 예측 분포 $P$ 에 수치적 점수를 할당하며, 점수가 높을수록 더 좋은 것이다. 참 데이터 생성 분포 $Q$ 에 대한 예측 $P$ 의 품질은 기대 점수 $S(P, Q) = \mathbb{E}_{y\sim Q}[S(P, y)]$ 로 측정된다. 점수 규칙은 예측 분포 $P$ 가 데이터 분포 $Q$ 와 일치할 때 기대 점수가 최대화되는 경우 적절한(proper) 것으로 간주된다:

S(P, Q) \le S(Q, Q)~~~~\text{for all distributions}~P.~~~~(8)

이 속성은 점수 규칙이 모델이 편향되거나 왜곡된 분포를 예측하도록 유도하지 않음을 보장한다. 나아가, 점수 규칙은 $P=Q$ 일 때만 등호가 성립하는 경우 엄격하게 적절한(strictly proper) 것으로 간주되며, 이는 최적의 점수가 참 분포를 보고할 때만 달성될 수 있음을 의미한다.

따라서 엄격하게 적절한 점수 규칙을 훈련 목표로 사용하는 것은 우리의 생성 헤드를 훈련하기 위한 강력하고 원칙적인 접근 방식이 된다. 왜냐하면 기대 점수를 최대화하는 것은 모델의 예측 분포가 참 분포와 일치하도록 유도하는 것과 동등하기 때문이다. 이 원칙은 최대 우도 추정(maximum likelihood estimation)의 직접적인 일반화를 제공하며, 여기서 음의 로그 우도(negative log-likelihood)는 로그 점수(logarithmic score)에 해당하는 특수한 경우이다. 연속 도메인에서는 우도를 다루기 어렵지만, 점수 규칙의 이론은 풍부한 대안군을 제공한다.우리는 에너지 점수(Energy Score), 즉 광범위한 생성 애플리케이션에서 효과적임이 입증된 엄격하게 적절한 점수 규칙을 사용하여 훈련 목표를 구성한다. 에너지 점수는 완전히 우도 비의존적이다. 즉, 확률 밀도를 평가하는 대신 샘플 간의 거리를 통해 예측과 관찰 간의 정렬(alignment)을 측정한다. 예측 분포

3.3.2 Energy Loss

우리는 에너지 점수(Energy Score), 즉 광범위한 생성 애플리케이션에서 효과적임이 입증된 엄격하게 적절한 점수 규칙을 사용하여 훈련 목표를 구성한다. 에너지 점수는 완전히 우도 비의존적이다. 즉, 확률 밀도를 평가하는 대신 샘플 간의 거리를 통해 예측과 관찰 간의 정렬(alignment)을 측정한다. 예측 분포 $P$ 와 ground truth 관찰 $\bold{y}$ 에 대한 에너지 점수는 다음과 같이 정의된다:

S(P, \bold{y}) = \mathbb{E}_{\bold{x}', \bold{x}^{''} \sim P}[\parallel \bold{x}^{'} - \bold{x}^{''} \parallel^\alpha]-2 \mathbb{E}_{\bold{x} \sim P}[\parallel \bold{x}-\bold{y} \parallel^\alpha], ~~~~(9)

여기서 $\bold{x}, \bold{x}^{’}, \bold{x}^{’’}$ 는 $P$ 에서 추출된 독립적인 샘플들이다. 이 점수는 $\alpha \in (0, 2)$ 인 모든 $\alpha$ 값에 대해 엄격하게 적절하다. 일반적으로 $\alpha$ 는 1로 설정된다. 이 점수 정의에는 두 가지 핵심 항이 있다: 첫 번째 항은 다양성을 장려하며, 모든 샘플이 동일하여 붕괴되거나 지나치게 확신하는 예측을 생성하는 모델에 페널티를 부과한다. 두 번째 항은 충실도를 장려하며, 모델의 예측이 근거 진실 관찰에 가깝도록 유도한다.

방정식 의 기댓값 때문에 에너지 점수를 정확하게 계산하는 것은 다루기 어렵지만, 우리는 이를 실용적인 손실 함수로 사용하기 위해 불편향 몬테카를로 추정량을 구성할 수 있으며, 이를 에너지 손실이라고 명명한다. 이를 위해, 우리는 각 단계 $i$ 에서 생성 헤드로부터 $N$ 개의 후보 샘플 ${\tilde{\bold{z}}_{i, 1}, ..., \tilde{\bold{z}}_{i, N}}$ 을 추출한다. 또한, 우리의 오토인코더가 토큰 덩어리를 고정된 지점으로 매핑하는 대신 조건부 가우시안 사후 분포 $\bold{z}_i \sim q({\cdot \mid \bold{x}_{(i-1)K+1;iK}})$ 로 매핑하는 고유한 속성을 활용한다. 단일 샘플 $z_i$ 에 의존하는 것은 에너지 손실에 높은 분산을 도입할 수 있기 때문에, 훈련을 안정화하기 위해 이 사후 분포로부터 $M$ 개의 타겟 샘플 $\bold{z}_{i, 1}, …, \bold{z}_{i, M}$ 을 추출한다. 이 샘플 세트들을 결합하여, 최종 에너지 손실은 다음과 같이 공식화된다:

L_{energy} = \sum^L_{i=1}(\frac{2}{NM}\sum^N_{n=1}\sum^M_{m=1} \parallel \bold{z}_{i, m} - \tilde{\bold{z}}_{i, n} \parallel - \frac{1}{N(N-1)}\sum_{n \not = k} \parallel \tilde{\bold{z}}_{i, n}-\tilde{\bold{z}}_{i, k} \parallel). ~~~~(10)

실제로, 우리는 $N=8$ 과 $M=100$ 으로 설정한다. 모델 샘플의 수 $N$ 은 생성 헤드의 평가를 필요로 하기 때문에 훈련 비용을 직접적으로 확장시킨다. 따라서 높은 훈련 효율성을 유지하기 위해 작은 $N$ 을 사용한다. 알려진 가우시안 사후 분포에서 타겟 벡터를 추출하는 오버헤드는 거의 무시할 수 있으므로, 손실의 분산을 줄이기 위해 큰 $M$ 을 사용할 수 있다.

이 우도 비의존적 훈련 목표의 주요 이점은 그 유연성이다. 이는 오직 생성 헤드로부터 샘플을 추출하는 능력만을 요구하므로, 내부 아키텍처에 최소한의 제약만을 가하여 우리가 탐색할 간단하고 효율적인 설계를 가능하게 한다.

3.3.3 Model Architecture

이제 우리 모델의 아키텍처에 대해 자세히 설명한다. 우리는 표준 트랜스포머 백본을 사용하며, 출력 측 생성 헤드와 입력 측 적응(input-side adaptation)에 중점을 둔 수정을 가한다.

Energy-Based Generative Head. 생성 헤드의 입력은 두 가지이다: 조건부 문맥을 제공하는 트랜스포머 백본의 은닉 상태 $\bold{h}_{i-1}$ 와 샘플링에 필요한 확률적 특성을 제공하는 무작위 노이즈 벡터 $\bold{\epsilon} \in \mathbb{R}^{d_{\text{noise}}}$ . $\epsilon$ 의 각 차원은 균일 분포 $U[-0.5, 0.5]$ 에서 독립적으로 추출된다. 은닉 상태 $\bold{h}_{i-1}$ 와 노이즈 벡터 $\epsilon$ 은 모두 독립적인 선형 계층에 의해 헤드의 내부 차원(우리는 이를 트랜스포머의 은닉 차원 $d$ 와 일치하도록 설정)에 맞게 투영된다.

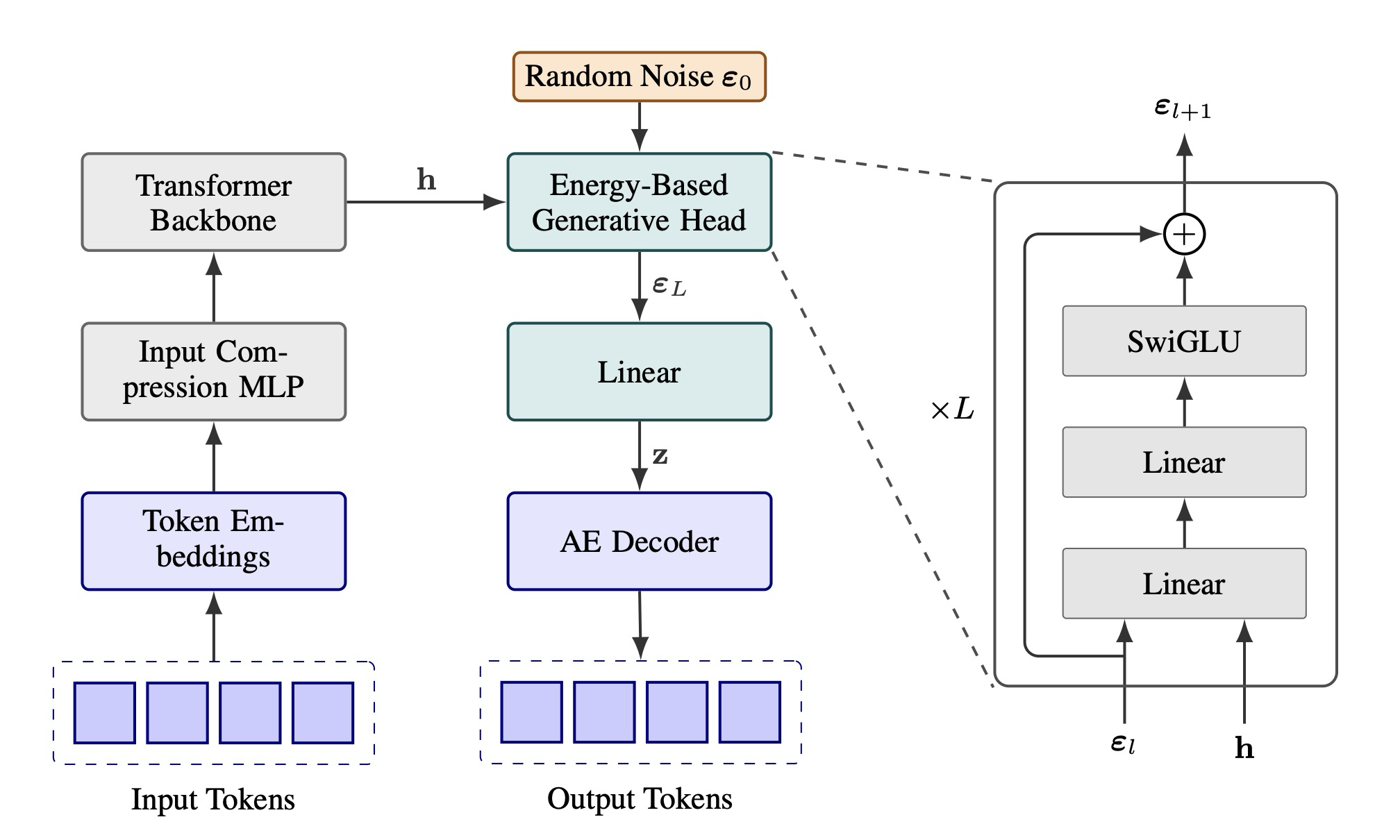
Figure 2: The Architecture of the Continuous Autoregressive Language Model (CALM)

생성 헤드의 핵심은 초기 노이즈 표현 $\epsilon_0 = \epsilon$ 을 최종 출력 벡터로 점진적으로 정제하는 $L$ 개의 잔차 MLP 블록 스택이다. 그림 2에 나타난 바와 같이, 각 MLP 블록은 먼저 두 개의 선형 계층을 통해 현재 표현 $\epsilon_l$ 을 은닉 상태와 융합시킨다. 이어서 중간 차원 $d$ 를 가진 SwiGLU 계층이 뒤따른다. 그런 다음 잔차 연결이 블록의 입력을 출력에 더한다. 이 과정은 표현을 대상 차원 $l$ 로 투영하는 최종 선형 계층으로 마무리되며, 출력 벡터 $\bold{z}_i$ 를 생성한다.

단일 MLP 블록은 약 $6d^2$ 개의 매개변수를 포함한다. 우리는 블록의 수를 트랜스포머 계층 수의 4분의 1로 설정하며, 따라서 전체 생성 헤드는 전체 모델 매개변수의 약 10%만을 차지하여 계산 오버헤드가 최소화된다.

Discrete Token Input. 모델의 입력에 대한 직관적인 접근 방식은 이전 단계에서 예측된 잠재 벡터 $\bold{z}_{i-1}$ 를 선형 투영을 사용하여 트랜스포머의 은닉 차원 $d$ 로 임베딩하는 것일 수 있다. 그러나, 우리는 경험적으로 이러한 잠재 벡터를 트랜스포머의 입력으로 사용하는 것이 성능의 눈에 띄는 저하로 이어진다는 것을 발견했다. 이는 모델이 그렇게 압축된 입력 표현에서 의미론적 정보를 풀어내는 데 어려움을 겪기 때문이다.

이러한 문제를 우회하기 위해, 우리는 모델의 자기회귀 프로세스를 이산 토큰 공간에 기반을 둔다. 훈련 중에 각 단계의 입력은 이전 단계의 $K$ 개 토큰으로 구성된다. 효율성을 유지하기 위해, 우리는 경량 입력 압축 모듈(2계층 MLP)을 사용하여 $K$ 개의 임베딩을 단일 입력 표현으로 매핑한다. 추론 과정은 다음과 같이 전개된다:

입력 처리: 단계 $i$ 에서, 이전에 생성된 $K$ 개 토큰 덩어리는 임베딩되고 단일 입력 표현으로 압축되어 트랜스포머에 공급된다.
연속 예측: 트랜스포머는 은닉 상태 $\bold{h}_{i-1}$ 를 출력하며, 우리의 에너지 기반 생성 헤드는 이를 사용하여 다음 연속 벡터 $\bold{z}_i$ 를 예측한다.
이산 피드백 루프: 예측된 벡터 $\bold{z}_i$ 는 사전 훈련된 오토인코더의 고정된 디코더 $g_{dec}$ 를 즉시 통과하여 다음 $K$ 개 이산 토큰을 재구성한다.

CALM의 전체 아키텍처는 그림 2에 설명되어 있다.

4. Likelihood-Free LM Evaluation

4.1 Principles of LM Evaluation

CALM 프레임워크는 내재적 생성 모델(implicit generative model)로 작동하며, 그 예측 확률 분포는 샘플링 프로세스를 통해 정의된다. 결과적으로, 명시적인 우도(likelihood)의 관점에서 정의되는 퍼플렉서티(Perplexity)와 같은 표준 언어 모델(LM) 평가 메트릭은 더 이상 모델 성능을 측정하는 데 사용될 수 없다. 더욱이, 훈련에 사용되는 에너지 손실(energy loss) 자체도 평가에는 부적합하다. 그 이유는 그 손실의 크기가 오토인코더에 의해 형성된 특정 잠재 공간에 주관적(subjective)이기 때문이다. 이로 인해 모델 불가지론적(model-agnostic) 평가 메트릭의 개발이 필요하며, 이는 원칙적이지만 완전히 우도 비의존적인 방식으로 언어 모델링 능력을 충실하게 평가할 수 있어야 한다.

평가 메트릭의 목표는 모델의 예측 분포 $P$ 와 참 데이터 분포 $Q$ 사이의 발산을 정량화하는 것이다. 이 원칙은 모델이 데이터 분포를 정확하게 복구할 때( $P=Q$ ) 메트릭이 유일하게 최적화된다는 속성으로 공식화된다. 이는 평가가 공정하며, 예측을 체계적으로 왜곡하는 모델에 의해 조작될 수 없음을 보장한다. 예를 들어, 전통적인 메트릭인 퍼플렉서티는 이 원칙의 대표적인 예이다. 이는 기대 음의 로그 우도에 기반을 두고 있으며, 이는 KL 발산과 데이터 엔트로피의 합으로 분해될 수 있다:

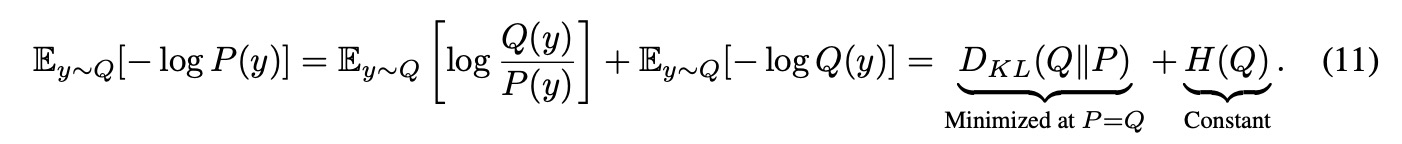
Formula 11

이 속성은 퍼플렉서티를 참 분포를 포착하는 모델 능력의 이론적으로 건전한 측정치로 확립하며, $P=Q$ 일 때 유일하게 최소화된다.

대조적으로, 관찰된 결과의 원시 우도( $P(y)$ )와 같은 순진한(naive) 메트릭은 이 원칙을 충족하지 못한다. 이 메트릭 하에서의 기대 점수 $\mathbb{E}_{y \sim Q}[P(y)]$ 는 가장 빈번한 단일 결과에 확률 1을 할당하는 결정론적 예측에 의해 최대화된다 (예: $P(\argmax_y Q(y))=1$ ). 이러한 메트릭은 기본 데이터 불확실성을 포착하지 못하는 지나치게 자신감 있는 모델에 잘못 유리하게 작용할 것이다. 이는 원칙적인 메트릭은 정확도에 대한 보상과 예측 불확실성의 올바른 표현 사이의 균형을 맞춰야 한다는 중요한 차이점을 강조한다. 순진한 우도 $P(y)$ 는 전자만을 다루기 때문에, 모델의 예측 품질을 측정하는 데 부적합하다.

4.2 BrierLM: Brier for Language Modeling

원칙적이고 우도 비의존적인 평가를 위해, 우리는 현대 신경망의 보정(calibration)을 평가하는 데 널리 사용되는 고전적인 엄격하게 적절한 점수 규칙인 브라이어 점수(Brier score) (Brier, 1950)로 눈을 돌린다. 예측 분포 $P$ 와 ground-truth 결과 $y$ 에 대한 브라이어 점수는 다음과 같이 정의된다:

\text{Brier}(P, y)=2P(y)-\sum_x P(x)^2. ~~~~ (12)

단순히 정확도만을 측정하는 원시 우도 $P(y)$ 와 달리, 브라이어 점수는 예측 불확실성을 정량화하기 위해 추가 항 $\sum_x P(x)^2$ 을 포함한다. 이 구조는 두 가지 상충되는 목표의 균형을 맞추며, 궁극적으로 잘 보정된 예측에 보상한다. 이 속성은 기대 브라이어 점수의 다음 분해를 통해 드러난다:

Formula 13

브라이어 점수는 이론적으로 건전하지만, 전체 예측 분포 $P$ 에 대한 지식을 요구하기 때문에 CALM에 대해 직접적으로 계산하는 것은 여전히 다루기 어렵다(intractable). 그러나 우리는 모델에서 추출한 샘플만을 사용하여 브라이어 점수에 대한 불편향 몬테카를로 추정량(unbiased Monte Carlo estimator)을 완전히 우도 비의존적인 방식으로 구성할 수 있음을 발견했다. 구체적으로, 불확실성 항 $\sum_x P(x)^2$ 은 두 독립적인 샘플의 충돌 확률로 해석될 수 있으며, 따라서 그 불편향 추정량은 $x_1, x_2 \sim P$ 일 때 단순히 지시 함수(indicator function) $I\{x_1 = x_2\}$ 이다. 유사하게, 정확도 항 $P(y)$ 은 $x \sim P$ 인 단일 샘플 $x$ 를 사용하여 $I\{x=y\}$ 로 추정될 수 있다.

이들을 결합하여, 우리는 모델에서 추출한 두 샘플을 사용하여 브라이어 점수에 대한 실용적이고 불편향적인 추정량을 구성한다:

\text{Brier}(P, y) \approx I\{x_1 = y\} + I\{x_2 = y\} - I\{x_1 = x_2\},\ x_1, x_2 \sim P. ~~~~ (14)

이 추정량은 CALM의 예측 능력을 우도 비의존적으로 평가할 수 있게 한다. 단순한 접근 방식은 교사 강제(teacher-forcing) 설정에서 다음 토큰 예측 성능을 평가하는 것일 수 있다. 이는 각 단계에서 두 개의 잠재 벡터를 생성하고, 고정된 오토인코더의 디코더를 사용하여 이를 디코딩한 다음, 각 결과 덩어리의 첫 번째 토큰만을 사용하여 브라이어 점수를 계산하는 것을 포함한다. 그러나 이러한 평가는 나머지 $K-1$ 개 토큰의 생성 품질을 무시하기 때문에 불충분하다. 이러한 한계를 해결하기 위해, 우리는 전체 n-그램에 걸쳐 브라이어 점수를 계산하는 메트릭인 Brier-n을 추가로 도입한다. 이 공식에서 추정량의 지시 함수는 n-그램을 단일의 원자적 결과(atomic outcome)로 취급한다. 마지막으로, BLEU(Papineni et al., 2002)와 같은 기존의 n-그램 기반 메트릭의 관례에 따라, 우리는 합성 메트릭인 BrierLM (Brier for Language Modeling)을 $n=1$ 부터 4까지의 Brier-n 점수의 기하 평균으로 정의하고, 이를 0-100 범위로 해석 가능하도록 100을 곱하여 조정한다:

\text{BrierLM} = 100 \cdot \left( \prod_{n=1}^4 Brier-n \right)^{0.25}. ~~~~ (15)

BrierLM의 유용성은 CALM을 넘어 확장되어, 기존의 자기회귀 모델에도 적용 가능한 보편적인 평가 프로토콜로 기능한다. 이러한 모델의 경우, BrierLM 추정량은 최종 소프트맥스 분포에서 샘플을 추출하는 것만으로 적용될 수 있으며, 이는 우리의 우도 비의존적 프레임워크와 직접적이고 공정한 비교를 가능하게 한다. 실제로, 우리의 기준선 자기회귀 모델에 대한 교차 엔트로피 손실과 BrierLM을 평가한 결과, BrierLM이 교차 엔트로피 손실과 매우 일치하며, 피어슨 상관계수 -0.966 및 스피어만 순위 상관계수 -0.991의 거의 선형적인 관계를 보여주었다. 이러한 강력한 단조 정렬은 BrierLM이 언어 모델링 능력의 신뢰할 수 있는 측정치임을 확인하며, 퍼플렉서티에 대한 신뢰할 수 있는 우도 비의존적 대안으로 확립한다.

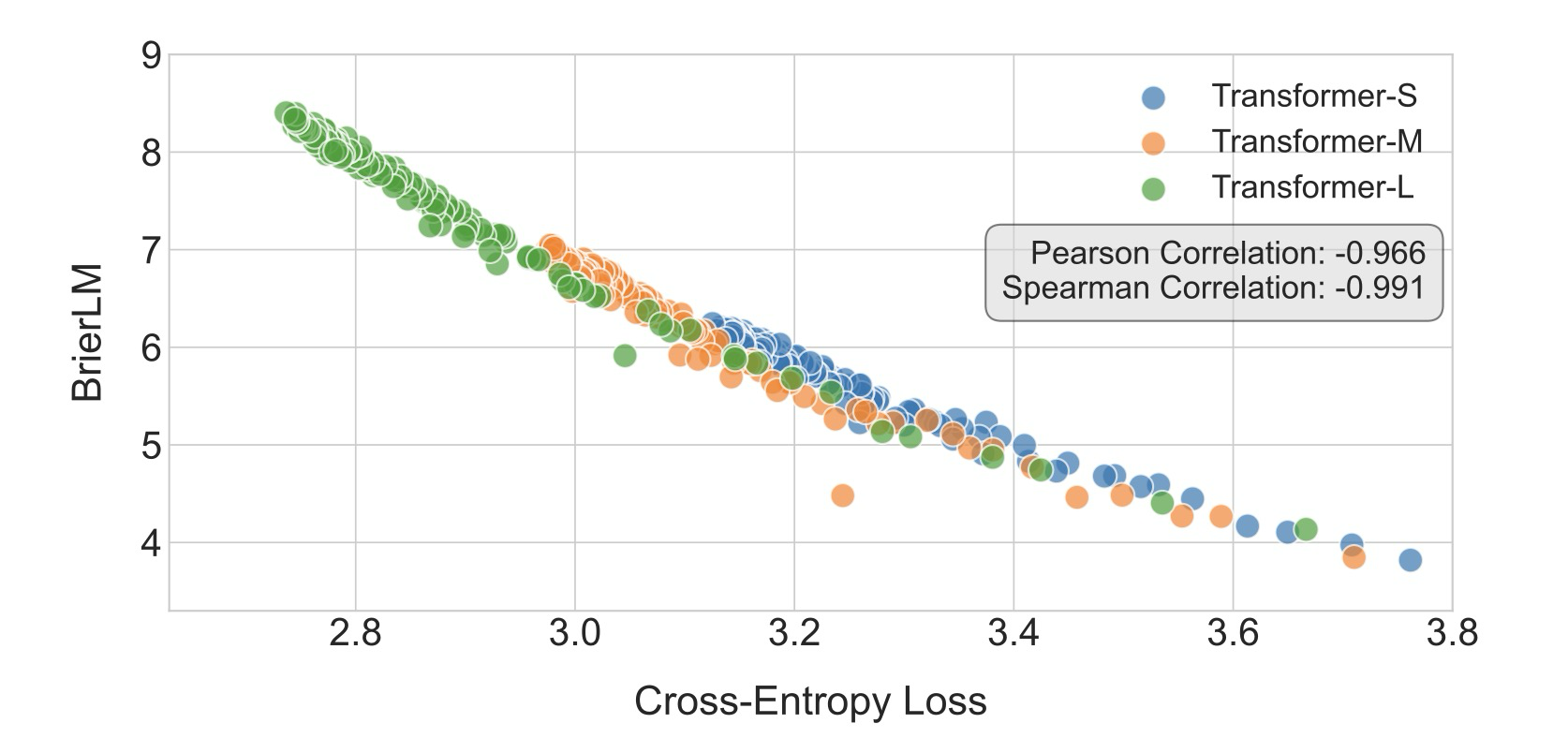
Figure 3: Joint distribution of the cross-entropy loss and the BrierLM score

더 나아가, BrierLM은 Diffusion 기반 언어 모델과 같은 암묵적 생성 모델(implicit generative models)의 증가하는 계층에 특히 중요한 이점을 제공한다. 이러한 모델은 역사적으로 퍼플렉서티를 근사하기 위해 변이형 하한(ELBOs)의 복잡하고 느슨한 추정에 의존했기 때문에 평가하기 어려웠다. BrierLM은 이러한 전체 문제를 우회하여, 그들의 언어 모델링 능력을 충실하게 평가하고, 다른 모델 계열 간의 공정한 비교를 가능하게 하는 직접적이고 불편향적인 방법을 제공한다.

5. Likelihood-Free Temperature Sampling

Algorithm 1: Likelihood-free Temperature Sampling

5.1 Exact Temperature Sampling via Rejection

Temperature 샘플링을 통한 제어된 생성은 최신 대규모 언어 모델(LLMs)의 필수적인 기능이다. 일반적으로 이 기술은 사전 소프트맥스(pre-softmax) 로짓을 재조정하여 구현되며, 이는 모델의 명시적인 확률 분포에 대한 접근을 요구한다. 그러나 이 접근 방식은 생성 헤드가 우도 비의존적(likelihood-free)이며 오직 표집기(sampler)만을 제공하는 우리의 CALM 프레임워크와 호환되지 않는다. 이는 블랙박스 샘플링만으로 temperature sampling을 수행해야 하는 중대한 과제를 제시한다. 이 섹션에서, 우리는 기각 샘플링(rejection sampling)의 원리에 기반을 두고 이 목표를 증명 가능하게 달성하는 정확한 알고리즘을 개발하여 이 과제를 해결한다.

우리 알고리즘에 대한 직관은 반복된 샘플링과 확률 지수화 사이의 관계에서 비롯된다. CALM의 맥락에서, 샘플 $x$ 는 각 단계에서 생성되는 완전한 $K$ 개 토큰 덩어리에 해당한다. temperature가 정수 $n$ 에 대해 $T=1/n$ 인 단순한 경우를 고려해 보자. 이 경우 목표 분포는 $P_t(x) \varpropto P(x)^n$ 이 된다. 샘플러에서 $n$ 번의 독립적인 시도에서 정확히 동일한 샘플 $x$ 를 추출할 확률 역시 $P(x)^n$ 이다. 이는 우아한 기각 샘플링 방식을 유도한다: 우리는 $n$ 개의 샘플을 추출하고, $n$ 개 샘플이 모두 동일한 경우에만 이를 수용한다. 그렇지 않으면 전체 세트를 기각하고 프로세스를 재시작한다. 수용된 샘플의 분포는 $P(x)^n$ 에 비례함이 증명되므로, 이는 우리의 일반 알고리즘의 토대를 제공한다.

이 접근 방식을 임의의 temperature $T \in (0, 1)$ 로 일반화하기 위해, 우리는 지수 $1/T$ 를 정수 부분 $n=\lfloor 1/T \rfloor$ 과 소수 부분 $\alpha = 1/T - n$ 으로 분해한다. 이 분해는 우리 알고리즘을 2단계 기각 표집 프로세스로 구조화한다. 첫 번째 단계는 위에서 설명한 반복 기반 방식을 사용하여 정수 구성 요소 $n$ 을 처리하며, $n$ 개의 독립적인 추출이 동일한 경우에만 후보 샘플 $x^*$ 를 생성한다. 소수 지수 $\alpha$ 를 처리하는 두 번째 단계는 베르누이 공장(Bernoulli Factory) 이론을 활용하여 성공 확률 $P(x)^{\alpha}$ 를 가진 편향된 동전 던지기를 시뮬레이션하는 반복 절차를 구성한다. 샘플은 두 단계를 모두 통과해야만 수용되며, 어느 시점에서든 실패하면 전체 프로세스가 재시작된다. 전체 절차는 알고리즘 1에 공식적으로 자세히 설명되어 있다. 다음 정리는 알고리즘의 정확성을 보장한다.

Theorem 1. 샘플러 $S$ 를 가진 암묵적인 이산 분포 $P(x)$ 와 temperature $T \in (0, 1)$ 에 대해, 알고리즘 1은 다음 분포에 따라 샘플을 생성한다:

P_T(x)=\frac{P(x)^{1/T}}{Z_T}, ~~~~ Z_T=\sum_x P(x)^{1/T}.

증거는 Appendix A.1에서 제공된다.

5.2 Expected Sampling Cost

알고리즘 1은 우도 비의존적 temperature 샘플링에 대한 정확한 해법을 제공하지만, 이의 실제적인 실현 가능성은 계산 효율성에 달려있다. 각 샘플러 호출은 생성 헤드와 오토인코더를 통한 순방향 통과(forward pass)를 포함하기 때문에, 핵심적인 우려는 이 알고리즘이 요구하는 예상 샘플링 횟수이다. 비록 이러한 순방향 통과가 추론 중에 병렬로 실행될 수 있다 하더라도, 엄청나게 많은 수의 표본이 요구된다면 심각한 계산 병목 현상을 초래할 수 있다. 다음 정리는 이 예상 샘플링 횟수에 대한 폐쇄형 표현식을 제공하며, 따름정리(Corollary) 2.1은 더욱 해석하기 쉬운 상한선을 제시한다. 증명은 부록 2(Appendix 2)에 제시되어 있다.

Theorem 2. 알고리즘 1을 사용하여 하나의 표본을 생성하는 데 필요한 기본 샘플러 $S$ 에 대한 예상 호출 횟수( $\mathbb{E} \lfloor N_{\text{total}} \rfloor$ )는 다음과 같다:

\mathbb{E} \lfloor N_{total} \rfloor = \frac{n+I(\alpha >0) \sum_x P(x)^{1/T-1}}{Z_T}

여기서 $Z_T = \sum_x P(x)^{1/T}$ 이고, $n= \lfloor 1/T \rfloor$ , $\alpha=1/T-n$ 이며, $I(\cdot)$ 는 지시 함수이다.

Corollary 2.1. temperature $T \in (0, 1)$ 에서 예상 샘플러 호출 횟수 $\mathbb{E} \lfloor N_{total} \rfloor$ 은 다음으로 제한된다:

\mathbb{E} \lfloor N_{\text{total}} \rfloor \le \begin{cases} \frac{1+n}{Z_T}, & \text{if}~ 0<T\le 0.5\\ \frac{1+\mid \chi \mid ^{2-1/T}}{Z_T}, & \text{if}~ 0.5<T<1 \end{cases}

여기서 $n= \lfloor 1/T \rfloor$ 이고 $Z_T=\sum_x P(x)^{1/T}$ 이다. $\mid \chi \mid$ 는 표본 공간의 크기를 나타낸다.

이러한 결과는 알고리즘의 실용성이 temperature $T$ 에 매우 민감함을 강조한다. 잠재적인 한계는 $T→ 1$ 일 때 처음 나타나는데, 이때 비용은 표본 공간의 크기 $\mid \chi \mid = \mid V \mid^K$ 까지 증가할 수 있다. 따라서 잠재적인 계산 병목 현상을 방지하기 위해 이 고온 영역(high-temperature regime)에서의 temperture 사용은 피하는 것이 좋다. 반대로, 저온 영역(low temperatures)에서는 정수 부분 $n= \lfloor 1/T \rfloor$ 이 커진다. 알고리즘의 성공은 $n$ 개의 동일한 표본을 추출하는 것을 요구하는데, 이는 $n$ 이 클 경우 발생할 확률이 극도로 낮아 매우 높은 기각률을 초래한다. 따라서 실용적인 유용성을 높이기 위해서는 표본 효율성이 더 높은 근사 알고리즘이 필요하다.

5.3 Batch Approximation

정확한 알고리즘의 실제적인 한계는 저온 영역(low-temperature regime)에서 가장 두드러지게 나타나며, 여기서 $n= \lfloor 1/T \rfloor$ 개의 동일한 샘플을 추출해야 하는 요구 사항은 극도로 높은 기각률을 초래하여 표본 활용률이 낮아진다. 이러한 문제를 해결하기 위해, 우리는 $T=1/n$ 형태의 저온에 맞춰진 효율적인 근사 알고리즘을 제안한다. 핵심 통찰력은 단일의 고위험 시도에서 $N$ 개의 큰 배치 내의 조합 검색으로 전환하는 것이다. 이러한 전환을 통해 단일 배치는 $\frac{N}{n}$ 개의 고유한 후보를 구성할 수 있으며, 이는 표본 활용률을 극적으로 향상시키고 단일 라운드에서 성공적인 일치를 찾을 확률을 높인다.

예를 들어, $T=0.5(n=2)$ 에서 표본을 추출하기 위해, 우리는 $N=10$ 개의 샘플 $A, C, A, D, B, E, A, F, B, G$ 배치를 추출할 수 있다. 여기서 샘플 $A$ 는 세 번 나타나고, 샘플 $B$ 는 두 번 나타난다. 알고리즘은 이 배치 내에서 성공적인 $n$ -튜플 후보의 수를 계산한다. 샘플 $A$ 의 경우, $\frac{3}{2}=3$ 개의 성공적인 후보가 있으며, 샘플 B의 경우, $\frac{2}{2}=1$ 개의 성공적인 후보만 있다. 마지막으로, 출력은 유효한 후보 $A, B$ 세트에서 가중된 확률 $(P(A)=3/4, P(B)=1/4)$ 에 비례하여 표본 추출된다.

어떤 샘플도 $n$ 번 이상 나타나지 않아 후보 세트가 비게 되는 드문 경우를 대비하여, 알고리즘이 항상 출력을 생성하도록 보장하기 위해 대체 메커니즘(fallback mechanism)이 도입된다. 이 메커니즘은 일치 요구 사항을 $n$ 에서 $n-1, n-2, …$ 로 반복적으로 줄여서 비어 있지 않은 후보 세트를 찾을 때까지 작동한다. 이 자세한 프로세스는 알고리즘 2에 설명되어 있다.

Algorithm 2: Approximate Temperature Sampling

어떤 유한 배치 크기 $N$ 에 대해서도 이 알고리즘은 편향될 수 있다. 이 편향은 출력 확률이 단일 확률적 배치 내에서 계산된 가중치의 비율에 의해 결정되기 때문에 발생하며, 비율의 기댓값이 일반적으로 기댓값의 비율과 같지 않기 때문이다. 그러나 이 알고리즘의 주요 강점은 점근적으로 편향되지 않는다는 것이다. 즉, 배치 크기 $N$ 이 무한대로 접근함에 따라 출력 분포는 참 목표 분포로 수렴한다. 이 무한대로 접근함에 따라 출력 분포는 참 목표 분포로 수렴한다.

Theorem 3.

\lim_{N \rightarrow \infin} P_{alg}(x;N)=P_T(x).

여기서 $P_{alg}(x;N)$ 은 배치 크기 $N$ 을 사용한 알고리즘 2의 표집 확률이며, $P_T(x)=P(x)^n/Z_T$ 는 temperature $T=1/n$ 에서의 참 목표 분포이다.

이러한 일관성(consistency) 속성은 알고리즘을 원칙적인 근사치로 확립하며, 여기서 배치 크기 $N$ 은 효율성과 정확도 간의 절충을 위한 실용적인 지렛대 역할을 한다. 알고리즘이 블랙박스 표집 인터페이스에만 의존하기 때문에, 그 유용성은 CALM 프레임워크를 넘어 전체 암묵적 언어 모델(implicit language models) 계층으로 자연스럽게 확장된다. 이는 이산 공간에서의 제어된 디코딩을 위한 보편적인 도구로서 그 위치를 확고히 한다.

6.1 Autoencoder

Latent Generative Modeling. 생성 모델링에서 두 단계 프로세스는 저명한 패러다임이다. 이 프로세스는 데이터의 압축된 잠재 표현을 먼저 학습하고, 그 잠재 공간 내에서 생성 모델을 훈련하는 방식으로 이루어진다. 이 접근 방식은 종종 고차원 데이터 공간에서 압축된 연속 잠재 공간으로의 매핑을 학습하는 변이형 오토인코더(Variational Autoencoder, VAE) (Kingma & Welling, 2014)로 시작한다. 이 원칙 덕분에 잠재 확산 모델(latent diffusion models)과 같은 현대 아키텍처는 연속 잠재 표현으로부터 고차원 데이터를 효율적으로 생성할 수 있다. 또 다른 경로는 벡터 양자화 VAE (Vector Quantized VAE, VQ-VAE) (van den Oord et al., 2017)로, 이는 입력을 유한하고 학습된 코드북으로 매핑하여 이산 잠재 공간을 학습한다. 이 접근 방식은 이미지나 오디오와 같은 연속 데이터의 자기회귀 생성에 기반이 되었다. 우리의 접근 방식은 이산-연속 매핑을 수행하는 독특한 방식을 도입한다. 효율성 추구에 의해 추진된 이 방법은 언어 생성을 위해 필요한 자기회귀 단계의 수를 상당히 감소시킨다.

Text Compression. 긴 텍스트를 압축된 벡터 표현으로 만드는 것은 시퀀스 모델링의 근본적인 개념이다. 예를 들어, RNN은 전체 시퀀스 히스토리를 단일 은닉 상태 벡터로 암묵적으로 압축하는 것으로 볼 수 있다. 대규모 언어 모델(LLMs) 시대에는 이 개념이 프롬프트 압축(prompt compression)에 초점을 맞추어 추론 효율성을 개선하는 방향으로 재활성화되었다. 예를 들어, Mu et al. (2023)은 수정된 어텐션 메커니즘을 설계하여 프롬프트 정보를 소수의 메모리 토큰으로 추출했다. Gao et al. (2024)은 높은 충실도의 압축을 촉진하기 위해 명시적인 재구성 목표를 추가로 도입했다. 근에는 Li et al. (2025), Kuratov et al. (2025), Mezentsev & Oseledets (2025)가 압축 한계를 최대 1568배까지 끌어올리며, 이산 텍스트 표현의 내재적인 희소성(sparsity)을 강조했다. 또한, DeepSeek-OCR (Wei et al., 2025)은 텍스트를 연속 이미지 토큰으로 압축하는 것을 시연하며 긴 컨텍스트 압축과 같은 응용 분야에서의 잠재력을 보여주었다. 이러한 방법들의 주된 초점은 프롬프트 압축에 있으며, 이는 결과 표현의 강건성(robustness)보다는 재구성 충실도(reconstruction fidelity)에 더 큰 중점을 둔다. 이와 대조적으로, 우리의 연구는 강건하고 매끄러운 잠재 다양체(smooth latent manifold)를 생성하는 것을 우선하며, 이는 안정적인 다운스트림 생성 모델링을 위한 중요한 전제 조건이다.

6.2 Likelihood-Free Language Modeling

Continuous Autoregressive Generation. 연속 벡터에 대한 자기회귀 생성은 이미지, 비디오, 오디오 합성(synthesis)과 같은 도메인에서 주목할 만한 성공을 거두며 떠오르는 연구 분야이다. GIVT는 가우시안 혼합 모델(Gaussian Mixture Model)로 타겟 벡터의 분포를 피팅함으로써 이 방향을 개척했다. 그러나 GIVT의 표현력은 사전 정의된 가우시안 혼합 분포군에 국한되며, 이는 복잡한 분포를 포착하는 능력을 제한하는 제약이다. Diffusion은 경량 확산 헤드(lightweight diffusion head)를 사용하여 벡터 분포를 모델링함으로써 GIVT의 한계를 극복했다. 이 방법은 더 표현력이 뛰어나지만, 반복적인 표집(sampling) 프로세스로 인해 추론 효율성 비용이 발생한다. 더 최근에는 엄격하게 적절한 점수 규칙(strictly proper scoring rules)에 기반한 일반적인 프레임워크를 소개했다. 에너지 트랜스포머(Energy Transformer)는 이 프레임워크의 구체적이고 강력한 사례로 제시되었으며, 고품질의 단일 단계 생성이 가능하다. 우리의 연구는 핵심 에너지 트랜스포머 프레임워크를 채택하지만, 언어 모델링의 특정 과제에 대한 성능과 안정성을 더욱 향상시키기 위해 생성 헤드 아키텍처, 에너지 손실, 그리고 모델의 입력 구조에 몇 가지 주요 개선 사항을 도입한다.

Parallel Token Prediction. 자기회귀 모델의 순차적 병목 현상을 극복하기 위해 여러 토큰을 병렬로 예측하려는 목표는 시퀀스 모델링에서 오랜 기간 추구되어 온 과제이다. 이 분야의 초기 노력은 단일 단계에서 전체 목표 문장을 생성하는 것을 목표로 하는 비자기회귀 기계 번역에서 개척되었다. 번역과 같이 고도로 제약된 조건부 작업에는 효과적이지만, 이러한 방법은 종종 개방형 언어 생성의 내재적인 다중 양식성(multi-modality)과 씨름한다. 다른 연구 분야에서는 다중 토큰 예측을 사용하여 훈련 신호를 풍부하게 하거나 추측 디코딩을 위한 후보를 제공하지만, 기본 생성은 여전히 단일 토큰 자기회귀 방식으로 남아 있다. 보다 직접적인 접근 방식은 계층적 모델링을 포함하며, 여기서 전역 모델(global model)이 큰 의미적 덩어리를 예측하고, 이는 지역 모델(local model)에 의해 디코딩된다. MegaByte는 전역 트랜스포머를 사용하여 토큰 블록을 예측하지만, 여전히 각 블록 내에서 토큰을 순차적으로 생성하기 위해 지역 자기회귀 모델에 의존한다. 개념적으로 우리의 연구와 더 가까운 Large Concept Models 또한 계층적 구조를 채택하며, 이들의 전역 모델은 연속적인 문장 임베딩을 자기회귀적으로 예측한다. 그러나 이 접근 방식은 우리의 CALM 프레임워크가 해결하도록 설계된 몇 가지 과제에 직면한다. 즉, 이들의 SONAR 오토인코더는 계산적으로 무겁고 취약하며, 확산 기반 생성 프로세스에 의존하여 반복적인 추론 병목 현상을 초래한다. 마지막으로, 병렬 생성을 위한 또 다른 패러다임은 텍스트용 확산 모델로, 전체 문장 또는 블록 수준에서 노이즈로부터 토큰 시퀀스를 반복적으로 정제한다. 현재 어려운 이산 토큰 공간에서 작동하는 이러한 모델은 우리 오토인코더가 제공하는 강건한 연속 공간으로부터 잠재적으로 이점을 얻을 수 있다.

6.3 Likelihood-Free LM Evaluation

LM metrics. 언어 모델 평가는 학습된 분포의 충실도 평가와 생성된 출력의 품질 평가를 분리하는 두 가지 별개의 패러다임으로 나뉜다. 우도 기반 메트릭은 퍼플렉서티(Perplexity)와 같이 학습된 분포를 평가하는 원칙적인 방법을 제공한다. 그러나 이러한 메트릭은 우도(likelihood)를 다룰 수 있는 모델로 제한된다. 다른 한편으로는, 표본 기반 메트릭이 있으며, 이는 생성된 출력에 초점을 맞춘 다양한 군을 형성한다. BLEU와 ROUGE 같은 고전적인 방법들은 생성된 텍스트를 참조 출력과 비교하여 그 품질을 평가한다. MAUVE나 LLM-as-a-judge와 같은 더 최근의 접근 방식들은 참조 없는 평가를 허용하지만, 이는 휴리스틱 또는 블랙박스 모델에 의존하며, 점수 규칙이 제공하는 형식적인 보장이 부족하다. 우리가 제안하는 메트릭인 BrierLM은 이 격차를 해소하도록 설계되었다. BrierLM은 오직 모델 표본에 의존하면서도, 엄격하게 적절한 점수 규칙으로서 퍼플렉서티와 유사하게 모델의 예측 품질에 대한 충실한 평가를 제공한다.

Brier Score. 브라이어 점수는 원래 확률론적 일기 예보를 평가하기 위해 브라이어(Brier)가 제안했다. 브라이어 점수는 엄격하게 적절한 점수 규칙의 고전적인 예이며, 모델이 최적의 점수를 달성하기 위해 참된 믿음(true belief)을 보고하도록 장려한다는 것을 이론적으로 보장한다. 결과적으로, 이는 분류 작업에서 확률론적 예측의 품질을 평가하고, 모델 보정(calibration)을 평가하는 데 널리 채택되었다. 우리 연구의 혁신은 두 가지이다: (1) 우리는 브라이어 점수를 우도 비의존적인 방식으로 불편향적으로 추정하는 방법을 도입한다. (2) 우리는 그 응용을 단순한 분류 작업에 대한 메트릭에서 언어 모델링 능력을 평가할 수 있는 메트릭으로 일반화한다.

6.4 Likelihood-Free Temperature Sampling

Bernoulli Factory. temperature 샘플링 문제는 베르누이 팩토리(Bernoulli Factory)의 고전적인 문제와 개념적으로 관련된다. 이 문제는 알려지지 않은 성공 확률 $p$ 를 가진 동전만을 사용하여 성공 확률 $f(p)$ 를 가진 새로운 동전을 시뮬레이션하는 과제를 다룬다. 이는 암묵적 분포 $P(x)$ 에 대한 기본 샘플러만을 사용하여 $P(x)^{1/T}$ 에 비례하는 목표 확률을 달성해야 하는 우리의 도전과제를 반영한다. 주요 차이점은 베르누이 팩토리 문제가 이진 결과(binary outcome)를 가정하는 반면, 우리는 대규모 이산 표본 공간에서 작동한다는 점이다. 우리의 2단계 알고리즘은 이 간극을 우아하게 연결한다. 첫 번째 단계는 단일 후보 $x^*$ 를 분리하여 문제를 이진 문제로 축소하며, 두 번째 단계는 기존 베르누이 팩토리 알고리즘을 직접 적용하여 $P(x^*)^{\alpha}$ 의 확률을 가진 이벤트를 구성한다.

Controlled Generation. 많은 생성 모델들이 온도 표집을 위한 명시적인 확률적 제어 기능이 부족하지만, 그들은 표본 품질과 다양성 간의 상충 관계를 조절하기 위한 대체 전략을 개발해 왔다. 예를 들어, VAE와 정규화 흐름(normalizing flows)은 종종 사전 잠재 분포의 분산(variance)을 조정하여 이를 달성한다. 적대적 생성 네트워크(Generative Adversarial Networks)에서는 절단 트릭(truncation trick)이 표집을 잠재 공간의 고밀도 영역으로 제한한다. 유사하게, 확산 모델(diffusion models)은 역 표집(reverse sampling) 과정에서 노이즈 분산을 변경하여 확률성을 제어할 수 있다. 그러나 이러한 기술들은 근본적으로 휴리스틱(heuristics, 발견적 방법)이며, 수정된 출력 분포의 형태를 특성화하는 것이 일반적으로 다루기 어렵고, 모두 잠재 공간과 같은 모델 내부 요소에 대한 화이트박스 접근(white-box access)을 필요로 한다. 이와 대조적으로, 우리의 연구는 이산 공간의 암묵적 모델로부터 온도 표집을 수행하기 위한 보편적인 블랙박스 알고리즘을 제안하며, 이러한 광범위한 모델 계층에 대해 증명 가능하게 정확한 방법을 제공한다.

7. Experiments

7.1 Settings

Model. 우리 모델은 표준 트랜스포머 백본을 기반으로 구축된다. 우리는 RMSNorm, SwiGLU 활성화, 로터리 위치 임베딩을 포함하여 LLaMA 계열의 아키텍처 설계를 대부분 채택한다.

Training Details. CALM 프레임워크의 훈련 프로세스는 2단계로 진행된다. 우리는 먼저 Pile의 150억 개 토큰 하위 데이터셋에서 일련의 오토인코더를 훈련시켜, 크기 $K \in \{1,2,4,8\}$ 인 토큰 덩어리를 연속 벡터로 매핑한다. 이 오토인코더들은 은닉 크기 512, 잠재 차원 $32K$ 를 사용한다. 이들은 약 75M(7천 5백만) 개의 매개변수를 가지며, 512k 토큰의 배치 크기로 30k 스텝 동안 훈련된다. 이어서, CALM 모델은 나머지 데이터에서 2백만 토큰의 배치 크기로 250k 스텝 동안 훈련된다. 컨텍스트 길이는 2048 스텝으로 설정되며, CALM의 경우 이는 $2048K$ 토큰에 해당한다. 모든 모델은 AdamW 옵티마이저를 사용하여 최적화되며, $\beta_1=0.9$ , $\beta_2=0.95$ , $\epsilon=1\epsilon-8$ 의 설정을 따른다. 우리는 $3 \times 10^{-4}$ 의 학습률을 사용하며, 이는 2000 스텝의 웜업과 함께 상수 스케줄을 가지고, 가중치 감소(weight decay)는 0.1, 그래디언트 클리핑(gradient clipping)은 1.0으로 설정된다.

7.2 Main Results

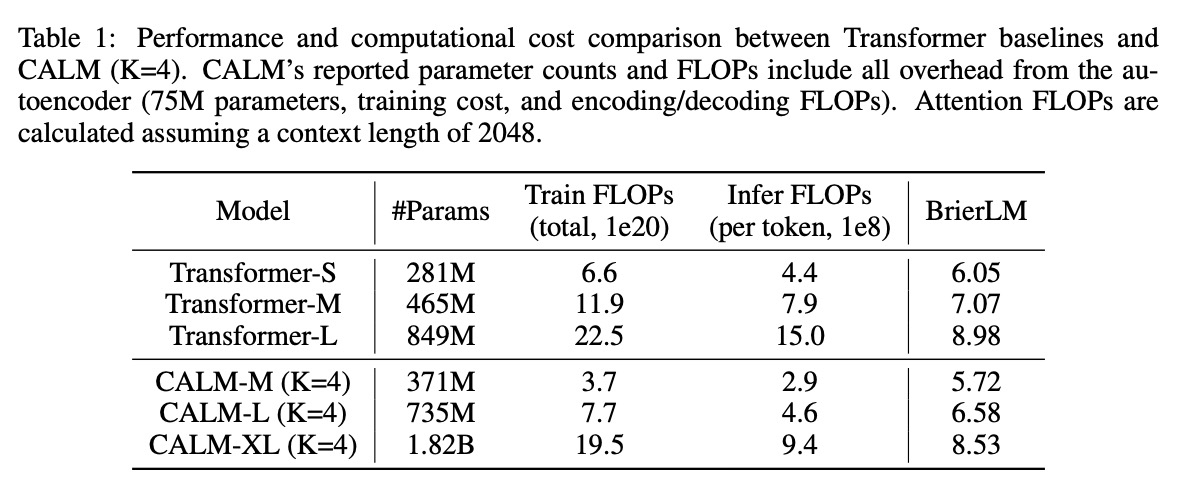
우리는 표준 트랜스포머 기준선과 CALM 프레임워크(고정된 덩어리 크기 $K=4$ )를 비교한 주요 결과를 표 1에 제시한다. 이 결과들은 CALM이 언어 모델링을 위한 새롭고 더 효율적인 성능-계산 경계선을 확립함을 보여준다. 각 자기회귀 단계의 의미적 대역폭을 증가시킴으로써, CALM은 매개변수 개수 면에서는 상당히 더 커질 수 있지만, 훈련 및 추론 모두에서 더 적은 FLOPs를 요구한다. 예를 들어, 371M 매개변수의 CALM-M 모델은 281M 매개변수의 Transformer-S 기준선과 비슷한 BrierLM 점수를 달성한다. 그러나 CALM-M은 Transformer-S보다 44% 더 적은 훈련 FLOPs와 34% 더 적은 추론 FLOPs를 요구한다. 또한, CALM은 모델 크기를 증가시켜 성능을 지속적으로 개선할 수 있으며, 이는 전통적인 트랜스포머와 마찬가지로 크기 확장의 이점을 얻는다는 것을 확인시켜 준다.

모델 크기를 확장하는 것 외에도, 우리 프레임워크는 의미적 대역폭 $K$ 를 성능-계산 상충 관계를 탐색하는 새로운 지렛대로 도입한다. 그림 4는 $K$ 값의 변화에 따른 CALM-L의 성능을 표준 트랜스포머 확장 곡선과 비교하여 보여준다.

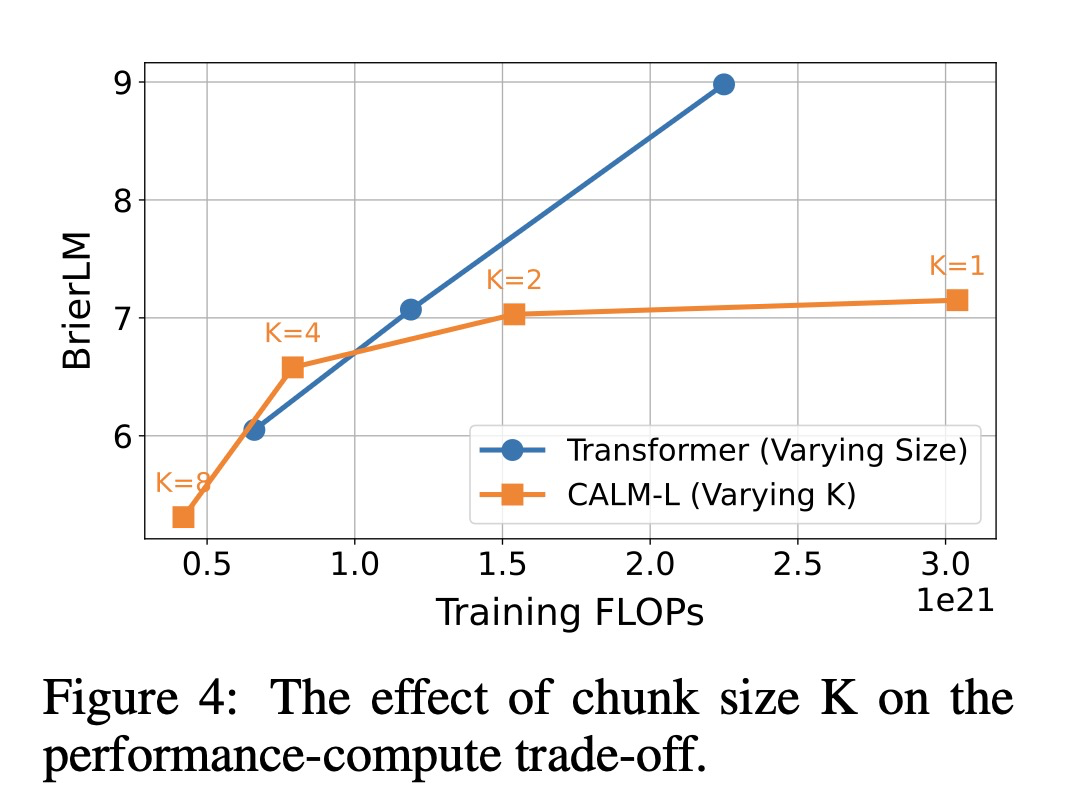
주목할 점은, $K=1$ 인 CALM-L은 이산형 대응 모델에 비해 더 낮은 성능에 더 많은 FLOPs를 요구하는 상당한 불리함을 안고 작동한다는 것이다. 이 격차는 모델이 더 도전적인 연속 예측 작업을 수행해야 하기 때문에 발생하며, 이는 향후 아키텍처 및 알고리즘 최적화를 위한 상당한 여지가 있음을 시사한다. $K$ 를 증가시킬 때 CALM의 이점이 명확해진다. $K=1$ 에서 $K=2$ 로 이동하면 성능 저하가 미미한 수준에 그치면서 비용이 거의 절반으로 줄어들며, $K=4$ 에서는 CALM 모델이 기준선의 성능-계산 경계선을 능가한다. 이 발견은 우리의 핵심 가설을 검증한다. 즉, 각 생성 단계의 의미적 대역폭을 확장하는 것이 언어 모델에서 성능-계산 상충 관계를 최적화하기 위한 새롭고 매우 효과적인 축을 제공한다는 것이다.

7.3 Effect of Autoencoder

본 절에서는 CALM 프레임워크의 최종 성능에 미치는 오토인코더 설계 선택의 영향을 연구한다. 오토인코더는 연속 언어 모델이 작동하는 잠재 공간을 정의하므로 핵심적인 구성 요소이다. 오토인코더의 영향을 분리하기 위해, 본 절의 모든 실험에서는 다운스트림 언어 모델을 고정한다. 이 모델은 은닉 크기 768, 12개 은닉 레이어, 16개 어텐션 헤드, FFN 중간 크기 2048, 3개의 MLP 블록으로 구성된 생성 헤드를 가진 에너지 트랜스포머이다. 각 모델 구성은 50,000 스텝 동안 훈련되었다. 별도로 명시하지 않는 한, 오토인코더는 7.1절에서 설명한 기본 매개변수를 사용한다. 우리는 제안된 각 기술의 기여를 검증하기 위한 포괄적인 제거 연구(ablation study)와 몇 가지 핵심 하이퍼파라미터의 영향에 대한 상세한 분석으로 논의를 시작한다.

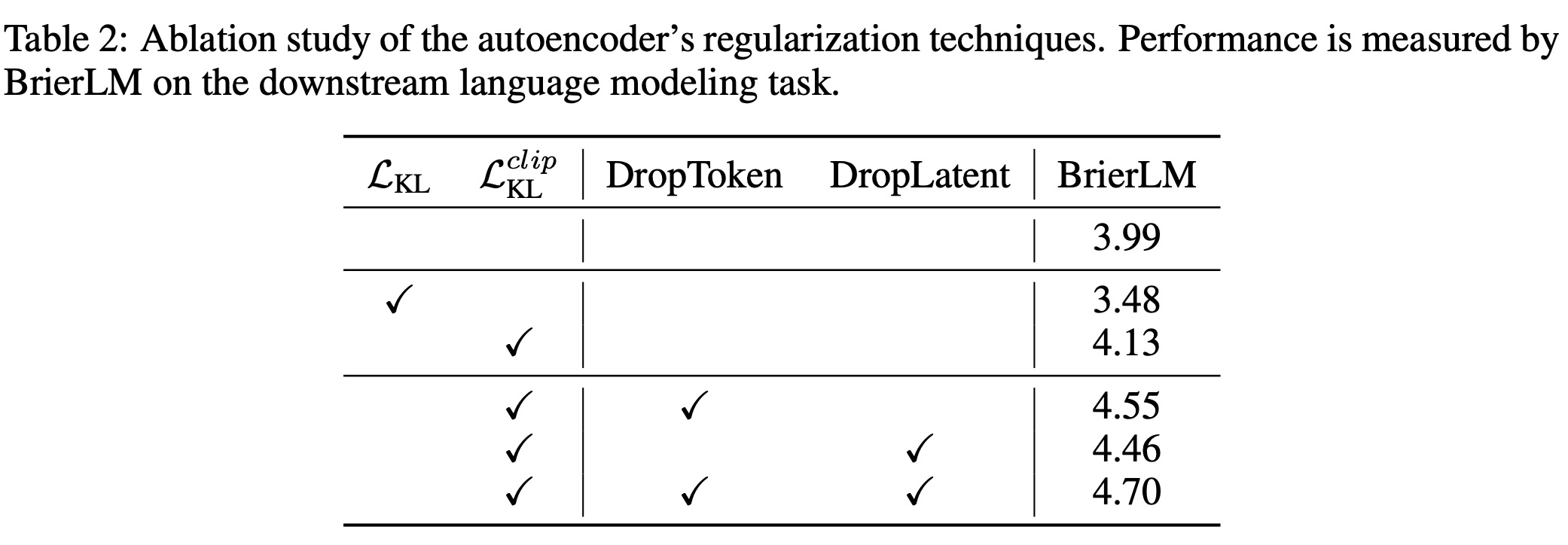
우리는 먼저 오토인코더의 설계 선택을 검증하며, 그 결과는 표 2에 상세히 나와 있다. 표준의 재구성 전용 오토인코더는 합리적인 기준선을 제공하지만, 변이형 목적 함수를 순진하게 통합하면 성능이 크게 저하되는 것으로 나타났다. 이러한 성능 저하는 심각한 사후 붕괴(posterior collapse) 사례로 거슬러 올라가는데, 128개 잠재 차원 중 71개가 표준 정규 사전으로 붕괴된 것이 발견되었다. KL 클리핑 전략의 도입은 이 문제에 대한 결정적인 해결책임이 입증되었는데, 이는 차원 붕괴를 효과적으로 방지하고 성능을 현저하게 향상시켰다. 나아가, 입력 토큰과 잠재 벡터 모두에 드롭아웃 정규화를 적용하는 것은 상당하고 직교하는(orthogonal) 성능 이점을 가져왔으며, 이는 각 기술이 높은 충실도와 강건성을 가진 잠재 공간을 형성하는 데 고유하게 기여함을 확인시켜 준다.

KL weight. 우리는 다음으로 재구성 충실도와 잠재 공간 정규화 사이의 균형을 조절하는 KL 발산 가중치 $\beta$ 에 대한 모델의 민감도를 조사한다. 우리는 $\beta$ 를 여러 자릿수에 걸쳐 변화시켰으며, 그 결과를 그림 6에 제시한다. KL 정규화가 없는 $(\beta=0)$ 기준선에서 시작하여, 소량의 변이형 정규화를 도입하면 최종 BrierLM 점수가 상당히 향상되는 것을 관찰한다. 이는 온건한 정규화가 잠재 다양체를 효과적으로 매끄럽게 하여 에너지 트랜스포머가 학습하기 더 쉽게 만들면서도, 재구성 정확도에는 거의 영향을 미치지 않는다는 우리의 가설을 확인한다. 그러나 정규화가 지나치게 공격적으로 되면 $(\beta=0.1)$ , 이러한 추세는 역전된다. $\beta=0.1$ 에서 BrierLM 점수가 급격히 하락하는데, 이는 오토인코더의 손상된 재구성 충실도(약 99%로 하락)와 직접적으로 연결되는 감소이다. 이러한 발견을 바탕으로, 우리는 $\beta=0.001$ 을 오토인코더 훈련을 위한 값으로 선택했다.

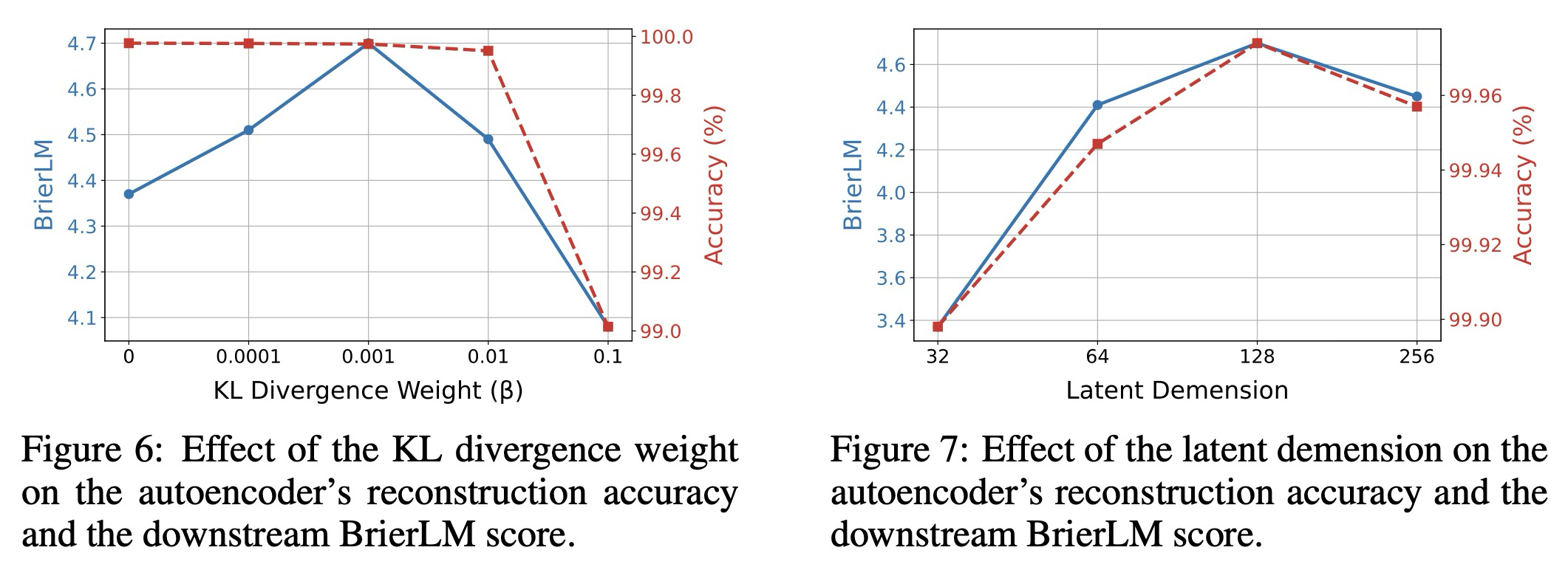
Latent Demension. 다음으로, 오토인코더의 정보 병목(bottleneck) 역할을 하는 잠재 차원 $l$ 의 영향을 조사한다. 우리는 잠재 차원 32, 64, 128, 256을 평가하고, 이에 따라 드롭아웃 비율을 0.05, 0.1, 0.15, 0.2로 조정했다. 결과(그림 7 참조)에서 볼 수 있듯이, 재구성 정확도는 모든 구성에서 일관되게 높게 유지되지만, 다운스트림 성능은 $l=128$ 에서 정점을 찍으며 달라진다. 이는 최적의 차원을 선택하는 데 상충 관계가 있음을 시사한다. $l=32$ 와 같이 잠재 공간이 너무 작으면 오토인코더가 지나치게 압축되고 취약한 표현을 학습하게 만든다. 반대로, 큰 잠재 차원은 오토인코더가 입력 토큰에서 잡음이 많거나 관련 없는 특징을 인코딩하도록 유도할 수 있으며, 이는 에너지 트랜스포머가 이 잡음을 모델링하는 데 유한한 용량을 소모하게 하여 기본 데이터 다양체를 식별하는 것을 더 어렵게 만든다. 따라서 $l=128$ 의 차원은 다운스트림 생성 모델을 위한 구조화되고 학습 가능한 잠재 공간을 유지하면서 강건한 표현을 위한 충분한 용량을 제공하는 최적의 균형을 이루는 것으로 보인다.

Scale. 마지막으로, 오토인코더의 규모 확장 영향을 조사한다. 우리는 인코더와 디코더 모두의 레이어 수를 두 배(4개)로 늘리고, 은닉 차원을 1024로 두 배 늘리며, 훈련 데이터셋을 100B 토큰으로 확장하는 등 여러 확장 축을 탐색했다. 흥미롭게도, 이러한 확장 노력 중 어느 것도 최종 BrierLM 점수에서 중요한 개선을 가져오지 못했다. 이러한 발견은 오토인코더의 작업이 본질적으로 단순하며 공격적인 규모 확장의 이점을 얻지 못함을 시사한다. 상대적으로 적당한 양의 데이터로 훈련된 경량 아키텍처만으로도 우리 프레임워크에 필요한 높은 충실도와 강건성을 가진 표현을 학습하기에 충분하다. 이는 오토인코더가 전체 시스템에서 계산적으로 무시할 수 있는 구성 요소가 되도록 허용하는 바람직한 속성이다.

7.4 Effect of Model Architecture

본 절에서는 CALM 모델 아키텍처에 대한 제거 연구(ablation studies)를 수행하여, 다양한 설계 선택이 모델 성능에 미치는 영향을 조사한다. 별도로 명시하지 않는 한, 모든 실험은 은닉 크기 768, 12개 은닉 레이어, 16개 어텐션 헤드, FFN 중간 크기 2048의 기본 구성을 사용하여 수행된다. 생성 헤드는 3개의 MLP 블록으로 구성되며, 모든 모델은 50,000 스텝 동안 훈련된다.

Diffusion and Flow Matching. 생성 헤드는 어떤 연속 생성 모델이라도 될 수 있기 때문에, 우리는 두 가지 저명한 선택인 diffusion과 flow matching을 대안으로 평가한다. 이 실험들을 위해, 우리는 확산 헤드와 일관된 아키텍처를 채택하며, 안정적인 학습을 촉진하기 위해 에너지 손실에 사용된 다중 샘플 접근 방식을 반영하여 입력 은닉 상태를 $N=8$ 회 복제한다. 론 중에는 기본적으로 100개의 반복 스텝을 사용한다. 플로우 매칭 모델의 경우, 우리는 중점 표집기(midpoint sampler)를 사용한다. 그림 8은 확산, 플로우 매칭, 그리고 에너지 기반 생성 헤드의 성능을 비교한다. 결과는 플로우 매칭과 우리의 에너지 기반 헤드가 확산 모델보다 성능이 우수하며, 눈에 띄는 성능 격차를 보임을 보여준다. 이 두 모델 중, 플로우 매칭이 더 빠른 초기 수렴을 보이는 반면, 우리의 에너지 기반 헤드는 더 높은 성능 상한에 도달한다.

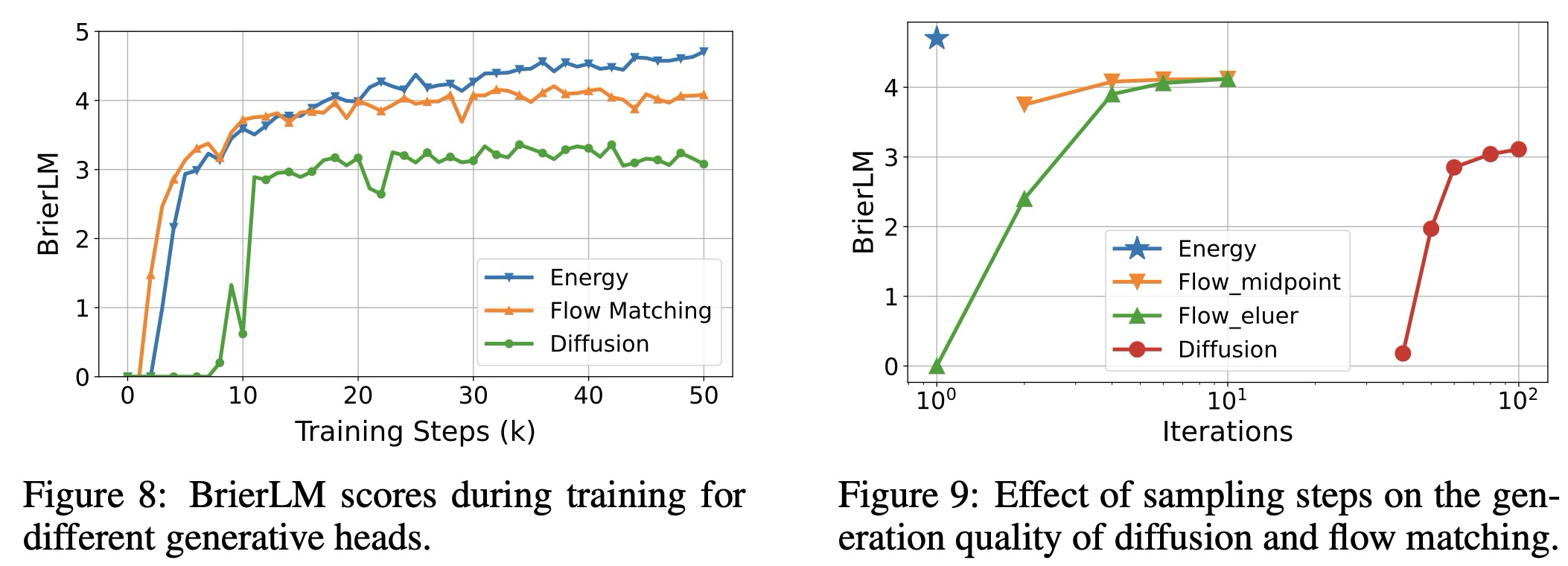
그림 9는 다양한 추론 반복 횟수에 따른 모델 성능을 추가로 비교한다. 플로우 매칭 모델의 경우 오일러(Euler) 및 중점 표집기를 모두 테스트했다. 보여지는 바와 같이, 확산 모델은 유효한 결과를 생성하기 위해 많은 반복 횟수를 요구한다. 이와 대조적으로, 플로우 매칭 모델은 상당히 더 효율적이며, 특히 중점 표집기는 단 2단계 만에 괜찮은 품질을 달성하고 4단계 내에서 거의 최적의 성능에 도달한다. 우리의 에너지 기반 생성 헤드는 두 가지 장점을 모두 제공한다. 우수한 성능을 제공하는 동시에 반복적인 디코딩의 필요성을 완전히 제거하여 CALM 프레임워크에 매력적인 선택이 된다.

Energy Loss. 다음으로, 우리는 모델 성능에 대한 에너지 손실 공식의 영향을 분석한다. 우리의 에너지 손실(수식 10)은 두 가지 표집 하이퍼파라미터를 포함한다: 모델 생성 샘플 수 $N$ 과 타겟 샘플 수 $M$ . $N$ 과 $M$ 의 값이 클수록 참 에너지 점수에 대한 더 나은 추정치를 제공하지만, 계산 비용도 증가시킨다. 우리의 기본 구성은 $N=8$ 과 $M=100$ 이다. 표 3은 $N$ 과 $M$ 을 변화시킨 결과를 보여주는데, 이는 성능과 계산 비용 간의 명확한 상충 관계를 드러낸다. 예상대로, 샘플 수를 증가시키면 BrierLM 점수가 지속적으로 향상되지만, 이는 훈련 비용이 거의 선형적으로 증가하는 결과를 낳는다. 따라서 우리의 기본 설정인 $N=8$ 과 $M=100$ 은 강건한 기울기 신호를 위한 적당한 크기의 $N$ 과 훈련을 안정화하기 위한 큰 $M$ 을 활용하는 균형 잡힌 구성으로 정당화된다.

우리는 또한 에너지 점수(수식 9)의 지수 $\alpha$ 의 영향을 조사한다. 이는 $\alpha \in (0,2)$ 에 대해 엄격하게 적절함이 보장된다. 표 4에 제시된 우리의 실험 결과는 이 이론적 속성과 일치한다. 우리는 $\alpha < 1$ 인 경우 훈련이 실패하는 것을 관찰했다. 이는 이전 연구에서 기울기 폭발 문제로 분석되었던 현상이다. $\alpha$ 값이 [1, 2) 범위 내에 있는 경우, 모델은 괜찮은 성능을 달성하며, 기본 설정인 $\alpha =1$ 에서 최상의 경험적 결과를 얻는다. $\alpha=2$ 에서는 모델의 BrierLM 점수가 0으로 하락한다. 이는 에너지 점수가 $\alpha=2$ 일 때 엄격하게 적절하지 않고 단지 적절하기 때문에 예상된 결과이다. 결과적으로, 에너지 손실은 더 이상 모델을 참 데이터 분포와 고유하게 일치시키도록 안내할 수 없으며, 이는 모델링 능력의 붕괴로 이어진다.

Model Input. CALM 프레임워크에서 중요한 설계 선택은 각 자기회귀 단계에서 트랜스포머 백본에 공급되는 입력 표현이다. 우리는 세 가지 구별되는 입력 방식을 평가한다: (1) 이산 입력 (Discrete input): 이전에 생성된 벡터 $\bold{z}_{i-1}$ 를 $K$ 개의 이산 토큰으로 디코딩한 다음, 임베딩 레이어와 입력 압축 MLP를 통해 다음 단계 입력으로 형성한다. (2) 연속 입력 (Continuous input): 벡터 $\bold{z}_{i-1}$ 를 단일 선형 레이어를 통해 트랜스포머의 은닉 차원으로 직접 투영하는 더 직접적인 대안이다. (3) 결합 입력 (Combined input): 이산 및 연속 방법의 표현을 요소별 합산을 통해 융합한다.

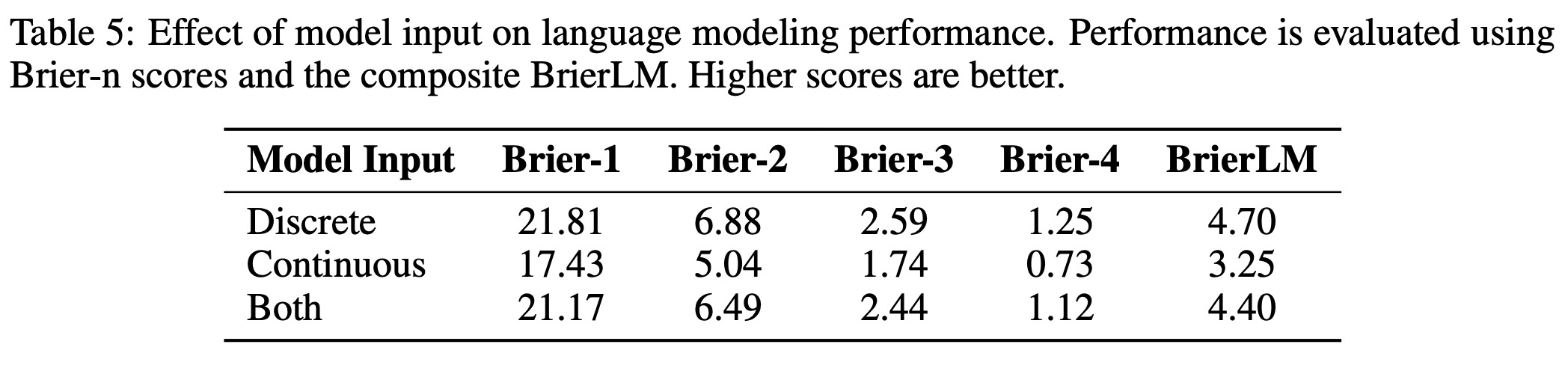
표 5에 요약된 바와 같이, 결과는 이산 입력 전략을 분명하게 선호한다. 결합 입력은 이점을 제공하지 못하고 성능을 약간 저하시키는 반면, 순수하게 연속적인 입력은 상당한 성능 저하를 초래한다. 이 결과는 우리의 가설을 확인시켜 준다. 즉, 연속 벡터가 이론적으로 해당 이산 토큰의 모든 정보를 포함하고 있음에도 불구하고, 매우 압축되고 취약한 특성으로 인해 모델이 기본 의미론적 정보를 풀어내는 것을 어렵게 만든다. 따라서 자기회귀 프로세스를 이산 토큰 공간에 기반을 두는 것은 더 구조화되고 안정적인 입력 신호를 제공하며, 이는 최적의 성능을 달성하는 데 중요하다.

7.5 Temperature Sampling

본 절에서는 우리의 배치 근사 temperature 샘플링 알고리즘(algorithm 2)의 실제적인 거동, 즉 예측 정확도와 생성 다양성 사이의 상충 관계를 알고리즘이 어떻게 탐색하는지 특성화하기 위해 상세한 분석을 수행한다. 이를 정량화하기 위해, 브라이어 점수 추정량 $\text{Brier}(P, y)$ 를 다음 두 가지 메트릭으로 분해한다:

정확도 $\mathbb{E}[I\{x=y\}]$ : 모델에서 추출된 단일 샘플이 근거 진실과 일치할 확률을 측정하며, 모델의 정확도를 직접적으로 반영한다.
충돌률 $\mathbb{E}[I\{x_1 = x_2\}]$ : 모델에서 추출된 두 개의 독립적인 샘플이 동일할 확률인 충돌 확률을 측정한다. 이는 다양성에 대한 역 프록시(inverse proxy) 역할을 하며, 충돌률이 높을수록 출력 분포가 덜 다양함을 나타낸다.

우리는 주요 BrierLM 메트릭과 일관되게, 정확도와 충돌률 모두에 대해 $n=1$ 부터 4까지의 $n$ -그램 점수의 기하 평균을 보고한다. 우리는 먼저 우리 알고리즘의 두 가지 핵심 하이퍼파라미터인 temperature $T$ 와 배치 크기 $N$ 이 이러한 메트릭에 미치는 영향을 조사한다. 구체적으로, 우리는 두 가지 실험 세트를 수행한다: 고정된 temperature $T=1/3$ 에서 배치 크기 $N \in \{1, 10, 20, 50, 100, 200, 500, 1000\}$ 을 변화시킨다. 고정된 배치 크기 $N=500$ 에서 temperature $T \in \{1/2, 1/3, 1/4, 1/5, 1/6 \}$ 을 변화시킨다.

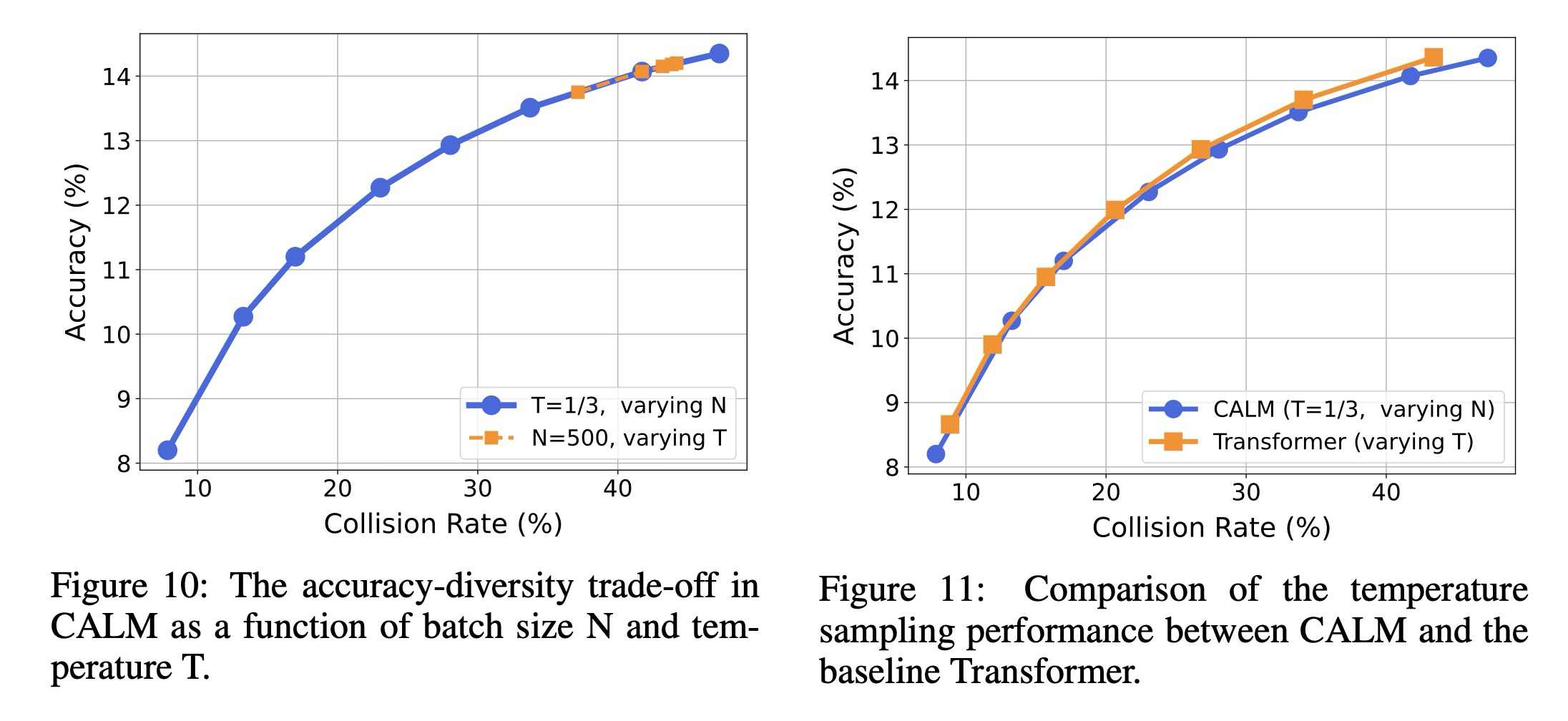
그림 10에 나타난 바와 같이, 배치 크기 $N$ 을 증가시키고 temperature $T$ 를 감소시키는 두 가지 방법 모두 출력 분포를 예리하게 만들어, 감소된 다양성(즉, 더 높은 충돌률)을 대가로 더 높은 정확도를 달성한다. 그러나 핵심 관찰은 배치 크기 $N$ 의 지배적인 역할인데, 이는 temperature $T$ 보다 훨씬 더 넓은 범위의 상충 관계를 포괄한다. 직관적으로, 더 큰 배치는 참 분포에 대한 더 명확한 통계적 그림을 제공하여, 고확률 후보를 더 쉽게 식별하고 자신 있게 출력할 수 있게 한다. 대조적으로, temperature $T$ 의 효과는 유한한 배치 내에서 사용 가능한 정보에 의해 제한된다. 따라서 온도는 기존의 목적을 수행하지만, 이러한 경험적 결과는 배치 크기 $N$ 이 우리의 우도 비의존적 프레임워크에서 정확도-다양성 경계를 탐색하기 위한 더 효과적인 도구임을 시사한다.

마지막으로, 우리는 우리의 표집 알고리즘의 거동을 전통적인 트랜스포머의 거동과 비교한다. 우리는 거의 동일한 BrierLM 점수를 가진 모델 체크포인트를 선택하여 공정한 비교를 보장한다. CALM의 경우, 온도를 $T=1/3$ 로 고정하고 배치 크기 $N$ 을 1부터 1000까지 변화시킨다. 트랜스포머 기준선의 경우, 소프트맥스 온도를 $T \in \{1, 0.9, …, 0.4\}$ 에 걸쳐 조정한다.

그림 11에 표시된 결과는 놀랍다. CALM에서 $N$ 을 조정하여 추적되는 정확도-다양성 궤적은 전통적인 트랜스포머에서 $T$ 를 조정하여 생성되는 궤적과 거의 동일하다. 이러한 일치성은 우리가 광범위한 온도 스펙트럼에 걸쳐 전통적인 모델의 생성 거동을 정확하게 복제할 수 있음을 보여준다. 예를 들어, $T=0.6$ 에 일치하는 것은 약 $N=100$ 의 배치 크기를 요구하는 반면, $T=0.5$ 의 더 낮은 온도를 시뮬레이션하는 것은 $N=200$ 의 더 큰 배치를 필요로 한다. 이는 더 낮은 온도, 더 높은 충실도의 생성을 시뮬레이션할 수 있는 능력이 샘플 수 증가라는 비용을 수반한다는 명확하고 예측 가능한 상충 관계를 시사한다.

8. Conclusion and Future Work

본 연구에서 우리는 LLM의 비효율적인 토큰별 패러다임에 도전하며, 생성 방식을 이산 토큰에서 단일 벡터가 $K$ 개 토큰을 나타내는 연속 벡터 공간으로 전환하는 CALM(Continuous Autoregressive Language Models) 프레임워크를 도입한다. 이러한 접근 방식을 지원하기 위해 우리는 포괄적인 우도 비의존적 도구 키트를 개발했다: 강건하고 높은 충실도의 오토인코더: 원본 토큰의 99.9% 이상의 정확도로 재구성이 가능하며, $K$ 개의 토큰 덩어리를 단일 연속 벡터로 압축한다. 생성 모델링을 위한 에너지 손실: 연속 도메인에서의 훈련을 위해 우도 기반 방식 대신 에너지 손실을 채택한다. LM 평가를 위한 BrierLM 메트릭: 우도에 접근할 수 없는 CALM에 적합하며, 엄격하게 적절한 점수 규칙인 Brier 점수를 기반으로 한다. 온도 표집을 위한 새로운 알고리즘: 이론적으로 정확한 표집을 위한 알고리즘과 효율적인 배치 근사(batch approximation)를 포함한다. 경험적 결과는 CALM이 우수한 성능-계산 상충 관계를 달성함을 보여주며, 이는 각 생성 단계의 의미적 대역폭을 확장하는 것이 LLM의 성능-계산 경계선을 미는 강력한 새로운 확장 축임을 강조한다. 예를 들어, $K=4$ 개의 토큰을 그룹화하는 CALM은 강력한 이산 기준선과 비슷한 성능을 달성하지만 훨씬 낮은 계산 비용으로 달성한다.

이러한 유망한 결과에도 불구하고, $K=1$ 인 CALM과 표준 트랜스포머 기준선 사이의 성능 격차에서 알 수 있듯이, CALM은 여전히 아키텍처 및 알고리즘 최적화를 위한 상당한 여지를 가지고 있다. 우리는 향후 연구를 위한 몇 가지 주요 영역을 식별한다:

Autoencoder. 현재 오토인코더는 재구성에 중점을 두지만, 향후 연구는 잠재 공간 내의 근접성이 의미적 유사성에 해당하도록 의미론적으로 기반을 둔 잠재 공간을 학습하는 오토인코더를 설계할 수 있다. 이는 다운스트림 생성 모델에 강력한 귀납적 편향(inductive bias)을 제공할 수 있다. 문맥 인식(context-aware) 또는 자기회귀적인 설계는 더 우수한 강건성과 더 신뢰할 수 있는 재구성을 제공할 수 있다.
Model. 현재 설계는 트랜스포머 백본 뒤에 경량 생성 헤드를 사용하지만, 더 통합된 종단 간(end-to-end) 생성 트랜스포머를 탐색하여 더 강력한 생성 모델링 능력을 얻을 수 있다. 에너지 손실은 강력한 기반을 제공하지만, 다른 엄격하게 적절한 점수 규칙이나 생성 모델을 조사하여 다른 최적화 역학 및 향상된 표본 품질을 제공할 수 있는지 탐색할 가치가 있다.
Sampling. 우리의 정확한 알고리즘은 거부 표집(rejection sampling)에 의존하여 상당한 추론 오버헤드를 초래할 수 있다. 향후 연구는 추론 시 다양성-충실도 상충 관계를 탐색하기 위한 더 경량의 휴리스틱 방법을 탐색할 수 있다. 이는 생성 헤드에 대한 입력 노이즈의 규모를 조작하거나, 수정된 손실 함수로 모델을 미세 조정하여 생성 거동을 유도하는 기술을 포함할 수 있다.
Scaling. 다음 핵심 단계는 CALM의 확장 속성을 조사하는 것이다. 더 큰 모델이 더 높은 의미적 대역폭을 지원하는 데 필요한 용량을 가질 것이라는 가설을 검증해야 한다. 기존의 확장 법칙(scaling laws)은 모델 및 데이터 크기의 함수로 성능을 모델링하지만, 우리의 프레임워크는 의미적 대역폭 K를 세 번째 변수로 도입한다. 통합 확장 법칙을 공식화하면 모든 계산 예산에 대해 최적의 K를 원칙적으로 선택할 수 있다.
Algorithmic Toolkit. 이산 토큰에서 연속 도메인으로의 패러다임 전환은 표준 LLM 알고리즘 도구 키트의 재평가를 필요로 한다. 예를 들어, 강화 학습의 정책 최적화는 CALM이 직접 계산할 수 없는 로그 확률을 증가시켜 모델을 업데이트하는 반면, 지식 증류(knowledge distillation)는 전체 확률 질량 함수에 대한 접근 없이 불가능한 KL 발산 최소화를 요구한다. 이러한 기술을 샘플 기반 체제에서 작동하도록 재공식화하는 방법은 향후 연구를 위한 중요한 질문이다.

Minki Hong

Developing AI systems that align with human social norms and values.

이전 포스트