Nested Learning: The Illusion of Deep Learning Architectures

Minki Hong·2025년 11월 24일

Paper Translate

목록 보기

3/7

Author: Ali Behrouz, Meisam Razaviyayn, Peiling Zhong, Vahab Mirrokni
Affilation: Google Research
Venue: NeurIPS 2025
Comments: arXiV 본이 나오면 업데이트 예정
Date: November 2025
Paper Link: https://abehrouz.github.io/files/NL.pdf

⭐️ Key Takeaways
1. 중첩 학습(Nested Learning, NL)은 기계 학습 모델을 각각 고유한 “컨텍스트 흐름”을 가진 일련의 중첩되고, 다단계이며, 병렬적인 최적화 문제들로 일관되게 표현하는 새로운 학습 패러다임이다.
2. NL 패러다임은 기존의 기울기 기반 옵티마이저(예: Adam, Momentum을 사용한 SGD 등)와 신경망 구성 요소가 실제로 자신의 컨텍스트 흐름을 압축하려는 연합 메모리 모듈임을 밝히며, 더 많은 “레벨”을 가진 표현력 있는 학습 알고리즘의 설계의 경로를 제시한다.
3. 본 논문은 장기/단기 메모리의 전통적인 관점을 일반화하는 연속체 메모리 시스템(Continuum Memory System)과 자기 참조 시퀀스 모델을 결합한 학습 모듈인 HOPE를 제시하며, 이는 언어 모델링 및 상식 추론 작업에서 베이스라인 모델들 대비 우수한 성능을 보여준다.

Abstract

지난 수십 년 동안, 더 강력한 신경 구조를 개발하고 이를 효과적으로 훈련하기 위한 최적화 알고리즘을 동시에 설계하는 것이 기계 학습 모델의 역량을 향상시키기 위한 연구 노력의 핵심이었다. 최근의 발전, 특히 언어 모델(LMs) 개발에서의 발전에도 불구하고, 이러한 모델이 어떻게 지속적으로 학습/기억하고, 스스로 개선하며, "효과적인 솔루션"을 찾을 수 있는지에 대한 근본적인 난제와 미해결 질문들이 존재한다. 본 논문에서, 우리는 중첩 학습(Nested Learning, NL)이라고 불리는 새로운 학습 패러다임을 제시하며, 이 패러다임은 모델을 각각 고유한 “컨텍스트 흐름”을 가진 일련의 중첩되고, 다단계이며, 병렬적인 최적화 문제들로 일관되게 표현한다. NL은 기존의 딥 러닝 방법들이 자체 컨텍스트 흐름을 압축함으로써 데이터로부터 학습한다는 것을 밝히며, 대규모 모델에서 인컨텍스트 학습(in-context learning)이 어떻게 출현하는지 설명한다. NL은 더 많은 "레벨"을 가진, 더 표현력이 풍부한 학습 알고리즘을 설계할 수 있는 경로(딥 러닝의 새로운 차원)를 제시하며, 이는 고차 인컨텍스트 학습 능력을 가져온다. NL은 신경 과학적으로 그럴듯하며 수학적으로 화이트박스적인 특성을 가질 뿐만 아니라, 우리는 다음의 세 가지 핵심 기여를 제시함으로써 그 중요성을 옹호한다: (1) 딥 옵티마이저(Deep Optimizers): NL을 기반으로, 우리는 잘 알려진 기울기 기반 옵티마이저(예: Adam, Momentum을 사용한 SGD 등)가 사실상 기울기 하강법(gradient descent)을 사용하여 기울기를 압축하려는 연관 메모리 모듈임을 보여준다. 이 통찰력을 바탕으로, 우리는 딥 메모리 및/또는 더 강력한 학습 규칙을 가진 보다 표현력이 풍부한 일련의 옵티마이저를 제시한다. (2) 자기 수정 타이탄(Self-Modifying Titans): 학습 알고리즘에 대한 NL의 통찰력을 활용하여, 우리는 자신의 업데이트 알고리즘을 학습함으로써 스스로 수정하는 방법을 배우는 새로운 시퀀스 모델을 제시한다. (3) 연속체 메모리 시스템(Continuum Memory System): 우리는 "장기/단기 기억"의 전통적인 관점을 일반화하는 메모리 시스템에 대한 새로운 공식을 제시한다. 이 자기 수정 시퀀스 모델을 연속체 메모리 시스템과 결합하여, 우리는 언어 모델링, 지속 학습, 그리고 장문 컨텍스트 추론 작업에서 유망한 결과를 보여주는 HOPE라는 학습 모듈을 제시한다.

1. Introduction

Figure 1: 뇌의 균일하고 재사용 가능한 구조와 다중 시간 규모 업데이트는 인간의 지속 학습을 구현하는 핵심 구성 요소이다. 중첩 학습은 뇌의 각 구성 요소에 대해 다중 시간 규모 업데이트를 허용하는 동시에, Transformer와 같은 잘 알려진 아키텍처가 사실상 다른 주파수 업데이트를 가진 선형 계층임을 보여준다.

수십 년 동안, AI 연구는 데이터로부터 학습하거나 경험으로부터 학습하는 기계 학습 알고리즘을 설계하는 데 초점을 맞춰왔다. 이는 종종 경사 기반 방법(gradient-based methods)을 사용하여 매개변수 $\theta \in \Theta$ 에 대한 목적 함수 $L(\theta)$ 를 최적화함으로써 이루어진다. 전통적인 기계 학습 기술은 특징 추출기(feature extractor)를 설계하기 위해 신중한 엔지니어링과 도메인 전문 지식을 요구했으며, 이는 자연 데이터로부터 직접 처리하고 학습하는 능력을 제한한다. 이후, 딥 표현 학습(deep representation learning)은 해당 작업을 위해 필요한 표현을 발견할 수 있는 완전 자동화된 대안을 제공한다. 그 결과, 딥 러닝은 화학 및 생물학, 게임, 컴퓨터 비전, 그리고 다중 모드 및 자연어 이해 분야에서 획기적인 성공을 거두면서 대규모 계산 모델의 필수적인 부분이 된다.

딥 러닝 모델에서 여러 계층을 쌓는 것은, 모델에 더 큰 용량(capacity), 복잡한 특징을 표현하는 데 더 나은 표현력, 그리고 더 많은 내부 계산(예: #FLOPS)을 제공하며, 이 모든 특징은 이전에 고정된 집합에 대한 분포 내(in-distribution) 예측을 요구하는 정적 작업에 필수적이며 바람직한 특징이다. 그러나 이러한 딥 디자인은 모든 문제에 대한 보편적인 해결책이 아니며, 여러 측면에서 모델의 표현력을 향상시키는 데 도움을 줄 수 없다. 예를 들면 다음과 같다: (i) 딥 모델의 계산 깊이는 더 많은 계층을 쌓아도 변하지 않을 수 있으며, 이는 전통적인 얕은 접근 방식과 비교하여 복잡한 알고리즘을 구현하는 능력을 그대로 남겨둔다. (ii) 일부 매개변수 클래스의 용량은 모델의 깊이/너비를 증가시켜도 미미한 개선만을 보일 수 있다. (iii) 훈련 과정은 주로 최적화 도구(optimizer)나 그 하이퍼파라미터의 차선책 선택으로 인해 차선책 해(suboptimal solution)로 수렴할 수 있다. (iv) 새로운 작업에 빠르게 적응하고, 지속적으로 학습하며, 분포 외(out-of-distribution) 데이터로 일반화하는 모델의 능력은 더 많은 계층을 쌓는다고 해서 변하지 않을 수 있으며, 더 신중한 설계를 필요로 한다.

위의 문제들을 극복하고 딥 러닝 모델의 역량을 강화하기 위한 노력의 핵심은 다음 사항들에 집중한다: (1) 더 표현력이 풍부한 매개변수 클래스(즉, 신경 아키텍처)를 개발하는 것; (2) 작업을 더 잘 모델링할 수 있는 목적 함수를 도입하는 것; (3) 더 나은 솔루션을 찾거나 망각에 더 탄력적인 더 효율적/효과적인 최적화 알고리즘을 설계하는 것; 그리고 (4) 아키텍처, 목적 함수 및 최적화 알고리즘이 "올바르게" 선택되었을 때, 표현력을 향상시키기 위해 모델 크기를 확장하는 것이다. 총체적으로, 이러한 발전과 딥 모델의 스케일링 패턴에 대한 새로운 발견들이 대규모 언어 모델(LLMs)이 구축된 토대를 마련한다.

LLMs의 개발은 딥 러닝 연구에서 중요한 이정표를 기록하며, "올바른" 아키텍처를 확장한 결과로 다양한 출현 능력(emergent capabilities)을 가진 보다 범용적인 시스템으로 패러다임이 전환된다. LLMs는 다양한 작업에서 모든 성공과 놀라운 능력을 보여줌에도 불구하고, 초기 배포 단계 이후에는 대체로 정적이다. 이는 사전 훈련 또는 사후 훈련 중에 학습한 작업은 성공적으로 수행하지만, 즉각적인 컨텍스트를 넘어서는 새로운 능력을 지속적으로 습득할 수는 없음을 의미한다. LLMs의 유일하게 적응 가능한 구성 요소는 인컨텍스트 학습(in-context learning) 능력이다. 이는 LLMs의 (출현하는 것으로 알려진) 특성으로, 컨텍스트에 빠르게 적응하여 제로샷 또는 소수샷 작업을 수행할 수 있게 한다. 인컨텍스트 학습을 넘어서 LLMs의 정적인 특성을 극복하기 위한 최근의 노력들은 계산 비용이 많이 들거나, 외부 구성 요소를 필요로 하거나, 일반화가 부족하거나, 또는 치명적인 망각(catastrophic forgetting)에 시달릴 수 있으며, 이는 연구자들이 기계 학습 모델을 설계하는 방법을 재검토해야 하는지, 그리고 지속적인 설정에서 LLMs의 역량을 발휘하기 위해 계층을 쌓는 것 이상의 새로운 학습 패러다임이 필요한지 질문하게 한다.

현재 모델은 단지 즉각적인 현재만을 경험한다. 비유로서, LLMs의 정적인 특성을 더 잘 설명하기 위해, 선행성 기억상실증(anterograde amnesia)의 예를 사용한다. 이 신경학적 상태는 환자가 장애 발병 후 새로운 장기 기억을 형성할 수 없지만, 기존 기억은 손상되지 않은 상태로 남아있는 경우이다. 이러한 상태는 그 사람의 지식과 경험을 짧은 현재의 창과 장애 발병 이전의 오랜 과거로 제한하며, 그 결과 즉각적인 현재를 마치 항상 새로운 것처럼 지속적으로 경험하게 한다. 현재 LLMs의 메모리 처리 시스템은 유사한 패턴을 겪는다. LLMs의 지식은 컨텍스트 창에 맞는 즉각적인 컨텍스트, 또는 "사전 훈련 종료" 시점 이전의 오랜 과거를 저장하는 MLP 계층 내의 지식으로 제한된다. 이러한 비유는 단기 기억을 통합하는 뇌의 방식과 신경생리학 문헌에서 영감을 얻도록 동기를 부여한다.

1.1 Human Brain Perspective and Neurophysiological Motivation

인간의 뇌는 지속 학습(효과적인 컨텍스트 관리라고도 함)에 관해서는 매우 효율적이고 효과적이며, 이는 종종 신경가소성(neuroplasticity) 덕분으로 여겨진다. 신경가소성은 새로운 경험, 기억, 학습, 심지어 손상에 반응하여 스스로 변화하는 뇌의 놀라운 능력이다. 최근 연구들은 장기 기억 형성이 최소한 두 가지 구별되지만 상호 보완적인 통합 과정(consolidation processes)을 포함한다는 것을 지지한다: (1) 빠른 "온라인" 통합 (시냅스 통합(synaptic consolidation)이라고도 함) 단계는 학습 직후 또는 곧 발생하며, 심지어 깨어있는 동안에도 발생한다. 이 단계는 새롭고 처음에는 취약한 기억 흔적(memory traces)이 안정화되고 단기 저장소에서 장기 저장소로 전송되기 시작하는 때이다. (2) "오프라인" 통합 (시스템 통합(systems consolidation)이라고도 함) 과정은 최근 부호화된 패턴의 재생(replay)을 반복한다. 이는 해마의 예파(SWRs) 동안 발생하며, 피질의 수면 방추(sleep spindles) 및 느린 진동과 조율되어, 기억을 강화하고 재구성하며 피질 부위로의 전송을 지원한다.

선행성 기억상실증의 비유로 돌아가면, 증거에 따르면 이 상태는 두 단계 모두, 특히 온라인 통합 단계에 영향을 미칠 수 있다. 이는 주로 해마가 새로운 서술 기억(declarative memories)을 부호화하는 관문이며, 해마의 손상은 새로운 정보가 장기 기억에 절대 저장되지 않음을 의미하기 때문이다. 위에서 언급했듯이, LLMs의 설계, 특히 Transformer 기반 백본은 사전 훈련 단계 이후에 유사한 상태를 겪는다. 즉, 컨텍스트에 제공된 정보는 장기 기억 매개변수(예: 피드포워드 계층)에 절대 영향을 미치지 않으므로, 정보가 여전히 단기 기억(예: 어텐션)에 저장되어 있지 않는 한, 모델은 새로운 지식이나 기술을 습득할 수 없다. 이 지점에서, 비록 두 번째 단계가 기억 통합에 동등하게 또는 훨씬 더 중요하고, 그것의 부재는 과정을 손상시키고 기억 상실을 초래할 수 있지만, 본 연구에서는 첫 번째 단계인 온라인 과정으로서의 기억 통합에 초점을 맞춘다. 우리는 부록 A에서 인간의 뇌 관점과 NL의 연결에 대한 추가 논의를 제공한다.

Notations 우리는 입력을 $x \in R^{N × d_m}$ 이라고 표기한다. $M_t$ 는 시간 $t$ 에서의 메모리/모델 $M$ 의 상태를 나타낸다. $K$ 는 키(keys), $V$ 는 값(values), $Q$ 는 쿼리(query) 행렬을 나타낸다. 아래 첨자 $t$ 가 붙은 굵은 소문자(예: $\bold{k}_t, \bold{v}_t, \bold{q}_t$ )는 입력 $t$ 에 해당하는 벡터를 나타내는 데 사용된다. 우리는 모든 개체 $f$ 의 분포를 $p(f)$ 로 나타낸다. 본 논문 전체에서 우리는 $L_M \ge 1$ 계층과 잔차 연결(residual connection)을 가진 단순 MLP를 메모리 모듈 $M(\cdot)$ 의 아키텍처로 사용한다. 필요할 때, 우리는 메모리 모듈은 $\theta_M \supe \{W_1, W_2, …, W_{L_M}\}$ 로 매개변수화하며, 이는 적어도 MLP의 선형 계층 매개변수를 포함한다. 우리는 중첩 학습의 다른 수준(다른 업데이트 주파수)에서의 매개변수를 참조하기 위해 괄호가 있는 위 첨자(예: $W^{(t)}$ )를 사용한다.

2. Nested Learning

이 섹션에서는 중첩 학습(Nested Learning, NL)의 동기, 공식적인 정의, 그리고 일반적인 높은 수준의 함의에 대해 논의한다. 우리는 연합 메모리(associative memory)의 공식화로 시작하며, 단계별 예시를 사용하여 아키텍처 분해의 이면과 신경망을 최적화 문제들의 통합된 시스템으로 모델링하는 것 사이의 연결에 대한 직관을 구축한다. 우리는 먼저 딥 러닝의 기존 방법과 개념들이 어떻게 NL 패러다임에 속하는지 보여주는 것을 목표로 하며, 그 후 전통적인 방법을 넘어서는 새로운 공식화들을 제시하고/또는 기존 알고리즘 및 설계를 개선하는 방법에 대한 통찰력을 제공한다.

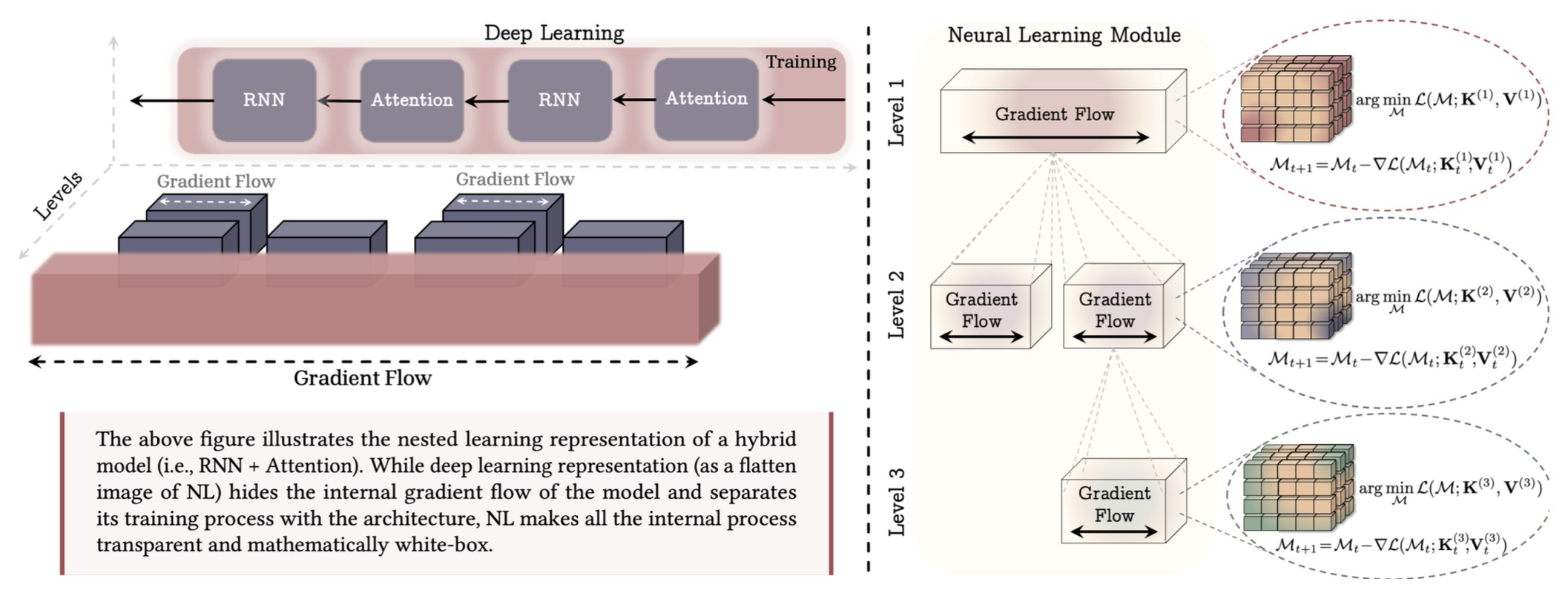
Figure 2: **기계 학습 모델과 그 훈련 절차를 일련의 중첩된 최적화 문제들로 표현하는 중첩 학습 패러다임**을 보여준다. (왼쪽) 하이브리드 아키텍처의 예시이며, NL의 평면화된 이미지로서의 딥 러닝 관점은 블록 내부 계산의 깊이에 대한 통찰력을 제공하지 않지만, NL은 모든 내부 기울기 흐름을 투명하게 표현한다. (오른쪽) 신경 학습 모듈(Neural Learning Module)인데, 이는 **자신의 컨텍스트 흐름을 압축하는 방법을 학습하는 계산 모델**이다. 예를 들어, 첫 번째 레벨은 모델의 가장 바깥쪽 루프 훈련(종종 "사전 훈련" 단계라고 불림)에 해당한다.

Figure 2: 기계 학습 모델과 그 훈련 절차를 일련의 중첩된 최적화 문제들로 표현하는 중첩 학습 패러다임을 보여준다. (왼쪽) 하이브리드 아키텍처의 예시이며, NL의 평면화된 이미지로서의 딥 러닝 관점은 블록 내부 계산의 깊이에 대한 통찰력을 제공하지 않지만, NL은 모든 내부 기울기 흐름을 투명하게 표현한다. (오른쪽) 신경 학습 모듈(Neural Learning Module)인데, 이는 자신의 컨텍스트 흐름을 압축하는 방법을 학습하는 계산 모델이다. 예를 들어, 첫 번째 레벨은 모델의 가장 바깥쪽 루프 훈련(종종 "사전 훈련" 단계라고 불림)에 해당한다.

2.1 Associative Memory

연합 메모리—사건들 사이의 연결을 형성하고 검색하는 능력—는 기본적인 정신 과정이며 인간 학습의 필수 불가결한 구성 요소이다. 종종 문헌에서 암기(memorization)와 학습(learning)의 개념이 혼용되어 사용되지만, 신경심리학 문헌에서는 이 둘이 명확하게 구별된다. 더 구체적으로, 신경심리학 문헌을 따라서, 우리는 메모리와 학습에 대한 다음 정의에 기반하여 용어를 구축한다.

Learning vs. Memorization:
메모리는 입력에 의해 야기되는 신경 업데이트이며, 학습은 효과적이고 유용한 메모리를 습득하는 과정이다.

본 연구에서, 우리의 목표는 먼저 옵티마이저와 신경망을 포함하여 계산 시퀀스 모델의 모든 요소가 자신의 컨텍스트 흐름을 압축하는 연합 메모리 시스템임을 보여주는 것이다. 광범위하게 말해서, 연합 메모리는 키(keys) 세트를 값(values) 세트로 매핑하는 연산자이다. 우리는 Behrouz 등의 연합 메모리에 대한 일반적인 정의를 따른다.

Definition 1 (Associative Memory). 키 $K \sube R^{d_k}$ 와 값 $V \sube R^{d_v}$ 의 세트가 주어지면, 연합 메모리는 두 세트의 키 $K$ 와 값 $V$ 를 매핑하는 연산자 $M:K \rightarrow V$ 이다. 데이터로부터 이러한 매핑을 학습하기 위해, 목적 함수 $\tilde{L}(\cdot ; \cdot)$ 는 매핑의 품질을 측정하며, $M$ 은 다음과 같이 정의될 수 있다:

M^*=\argmin_M~~~~\tilde{L}(M(K);V).~~~(1)

연산자 자체는 메모리이고 매핑은 암기 과정(즉, 컨텍스트 내 사건들의 연결을 암기하는 것)의 역할을 하는 반면, 데이터에 기반하여 그러한 효과적인 연산자를 획득하는 것은 학습 과정이다. 여기서 키와 값은 메모리가 매핑하고자 하는 임의의 사건일 수 있으며 토큰에 국한되지 않는다는 점에 주목해야 한다. 이 섹션의 후반부에서, 컨텍스트 흐름이 주어질 때 키와 값이 토큰, 기울기(gradients), 서브 시퀀스 등일 수 있음을 논의한다. 게다가, 연합 메모리라는 용어가 신경 과학 및 신경심리학 문헌에서 더 흔하지만, 위의 공식화는 데이터 압축 및 저차원 표현과도 밀접하게 관련된다. 즉, 식 1의 최적화 과정을 네트워크 $M(\cdot)$ 의 훈련 과정으로 해석할 수 있으며, 이 네트워크는 매핑을 자신의 매개변수로 압축하여 이를 더 낮은 차원의 공간에 표현하는 것을 목표로 한다.

키와 값이 입력 토큰(예: 토큰화된 텍스트)인 시퀀스 모델링에서, 식 1을 해결하기 위한 목적 함수 및 최적화 과정의 선택은 글로벌/로컬 소프트맥스 어텐션 또는 다른 현대적인 순환 모델과 같이 뚜렷한 시퀀스 모델링 아키텍처를 초래할 수 있다. 시퀀스 모델에 대한 이 단순한 공식화는 그 내부 과정에 대한 더 나은 이해를 제공하고, 또한 목적 함수와 최적화 과정을 기반으로 모델링 능력을 간단히 비교할 수 있는 도구를 제공한다. 다음에서, 단계별 예시를 사용하여 이 공식화가 신경 아키텍처의 모든 구성 요소(사전 훈련에서의 최적화 과정을 포함하여)에 어떻게 적용될 수 있는지, 그리고 실제로 모델이 각각 고유한 컨텍스트 흐름을 가진 다단계, 중첩 또는 병렬 메모리의 통합 시스템인지에 대해 논의한다.

A Simple Example of MLP Training. 우리는 간단한 예시로 시작하며, 이 예시에서는 경사 하강법(gradient descent)을 사용하여 목적 함수 $L(\cdot ; \cdot)$ 를 최적화함으로써 작업 $T$ 에 대해 데이터셋 $D_{\text{train}}=\{x_1, ..., x_{\mid D_{\text{train}}\mid}\}$ 상에서 1-계층 MLP(매개변수 $W$ 로 매개변수화됨)를 훈련하는 것을 목표로 한다. 이 경우, 훈련 과정은 다음 최적화 문제와 동일하다:

W^*=\argmin_W~L(W;D_{\text{train}}), ~~~(2)

경사 하강법에 의한 최적화는 다음의 가중치 업데이트 규칙을 초래한다:

W_{t+1}=W_t-\eta_{t+1}\nabla_{W_t}L(W_t;x_{t+1})~~~~(3)\\=W_t-\eta_{t+1}\nabla_{y_{t+1}}L(W_t;x_{t+1})\otimes x_{t+1},~~~~\text{where}~ x_{t+1} \sim D_{\text{train}},~~~~(4)

여기서 $y_{t+1}=W_{x_{t+1}}$ 은 입력 $x_{t+1}$ 에 대한 모델의 출력이다. 이러한 공식화가 주어지면, $u_{t+1}=\nabla_{y_{t+1}}L(W_t;x_{t+1})$ 로 설정하고 역전파 과정을 입력 데이터 포인트 $D_{\text{train}}$ 를 해당 $u_{t+1}$ 로 매핑하는 최적의 연합 메모리를 찾는 최적화 문제의 해로 재구성할 수 있다. 즉 우리는 $M(\cdot)=W_t \cdot$ 가 메모리를 매개변수화하도록 하고, dot-product similarity를 사용하여 $x_{t+1}$ 와 $\nabla_{y_{t+1}}L(W_t;x_{t+1})$ 사이의 $W_t$ 의 매핑 품질을 측정한다:

W_{t+1}=\argmin_W \langle W_{x_{t+1}},u_{t+1} \rangle + \frac{1}{2\eta_{t+1}}\| W-W_t \|^2_2 ~~~~(5)\\ =\argmin_W \langle W_{x_t}, \nabla_{y_{t+1}}L(W_t;x_{t+1}) \rangle + \frac{1}{2\eta_{t+1}} \| W-W_t \|^2_2.~~~~(6)

위의 공식화에서, $u_{t+1}=\nabla_{y_{t+1}}L(W_t;x_{t+1})$ 는 현재 출력과 목적 함수 $L(\cdot ; \cdot)$ 가 강제하는 구조 사이의 불일치를 정량화하는 표현 공간에서의 지역 놀람 신호(Local Surprise Signal, LSS)로 해석될 수 있다. 그러모르 이 공식화는 모델의 훈련 단계를, 데이터 샘플을 표현 공간에서의 LSS로 매핑하는 효과적인 메모리를 획득하는 과정으로 변환한다. 따라서, 이 예시에서 우리 모델은 데이터 샘플에 대한 단일 기울기 흐름을 가지며, 이는 데이터셋 $D_{\text{train}}$ 상에서만 활성화되고 그 이후의 다른 데이터 샘플(추론 또는 테스트 시간이라고도 함)에 대해서는 고정된다.

다음으로, 위의 예시에서 경사 하강법 알고리즘을 향상된 모멘텀 기반 변형으로 대체하면, 다음과 같은 업데이트 규칙이 초래된다:

W_{t+1}=W_t~-~\bold{m}_{t+1},~~~~(7) \\ \bold{m}_{t+1}=\bold{m}_t~-~\eta_{t+1}\nabla_{W_t} L(W_t;x_{t+1}) = \bold{m}_t~-~\eta_{t+1}\nabla_{y_{t+1}}L(W_t;x_{t+1}) \otimes x_{t+1}. ~~~~(8)

식 8에서, 식 7의 이전 상태(시간 $t$ 에서)가 주어질 때, $\nabla_{W_t}L(W_t;x_{t+1})$ 또는 유사하게 $\nabla_{y_{t+1}}L(W_t;x_{t+1})$ 의 값은 식 8의 순환과 독립적이므로 사전에 계산될 수 있다. 이를 위해, $u_{t+1}=\nabla_{W_t}L(W_t;x_{t+1})$ 로 두고, 식 8은 다음과 같이 재구성될 수 있다:

W_{t+1}=W_t-\bold{m}_{t+1},~~~~(9)\\ \bold{m}_{t+1}=\argmin_{\bold{m}}~- \langle \bold{m},\nabla_{W_t}L(W_t;x_{t+1}) \rangle + \eta_{t+1} \| \bold{m} -\bold{m}_{t} \|^2_2~~~~(10)\\ =\argmin_{\bold{m}}~-\langle \bold{m} x_{t+1},\nabla_{y_{t+1}}L(W_t;x_{t+1}) \rangle+\eta_{t+1} \| \bold{m}-\bold{m}_t \|^2_2,~~~~(11)

여기서 식 10의 최적화 문제는 적응형 학습률 $\eta_{t+1}$ 을 가진 경사 하강법의 한 단계와 동일하다. 이러한 공식화가 주어지면, 모멘텀 항은 (1) 기울기를 자신의 매개변수로 압축하는 키 없는(key-less) 연합 메모리, 또는 (2) 데이터 포인트를 해당 LSS 값으로 매핑하는 방법을 학습하는 연합 메모리로 해석될 수 있다. 흥미롭게도, 이 공식화는 모멘텀을 사용한 경사 하강법이 실제로 메모리가 단순한 경사 하강법 알고리즘에 의해 최적화되는 2단계 최적화 과정임을 보여준다. 이 과정은 가중치 업데이트 과정(식 9)이 느린 네트워크이고 그 모멘텀 가중치가 빠른 네트워크 (식 10)에 의해 생성되는 빠른 가중치 프로그램(FWPs)과 밀접하게 관련된다.

위의 예시들을 결론짓자면, 우리는 (1) 경사 하강법을 사용한 1-계층 MLP의 훈련 과정은 데이터 포인트를 해당 LSS 값으로 매핑하는 방법을 학습하는 1단계 연합 메모리이며, (2) 모멘텀을 사용한 경사 하강법은 내부 레벨이 기울기 값을 자신의 매개변수에 저장하는 방법을 학습하고, 외부 레벨이 내부 레벨 메모리의 값으로 느린 가중치( $W_t$ )를 업데이트하는 2단계 연합 메모리(또는 최적화 과정)임을 관찰한다. 이것들이 아키텍처와 옵티마이저 알고리즘 모두에 관하여 가장 간단한 예시들이지만, 더 복잡한 설정에서도 유사한 결론을 내릴 수 있는지 질문할 수 있다.

An Example of Architectural Decomposition. 다음 예시에서는 MLP 모듈을 선형 어텐션(linear attention)으로 대체한다. 즉, 경사 하강법으로 목적 함수 $L$ 을 최적화하여 작업 $T$ 에 대해 시퀀스 $D_{\text{train}}$ 상에서 1-계층 선형 어텐션을 훈련하는 것을 목표로 한다. 정규화되지 않은 선형 어텐션 공식화를 상기하면 다음과 같다:

\bold{k}_t=x_tW_{\bold{k}}, ~~~~\bold{v}_t=x_tW_{\bold{v}},~~~~\bold{q}_t=x_tW_{\bold{q}}, ~~~~(12)\\ M_t=M_{t-1}+\bold{v}_t\bold{k}_t^T,~~~~(13)\\ y_t=M_t\bold{q}_t.~~~~(14)

이전 연구들에서 논의되었듯이, 식 13의 순환은 행렬 값 연합 메모리 $M_t(\cdot)$ 의 최적화 과정으로 재구성될 수 있으며, 이는 키와 값의 매핑을 자신의 매개변수로 압축하는 것을 목표로 한다. 더 자세히는, 정의 1에서, 우리가 $\tilde{L}(M_{t-1};\bold{k}_t,\bold{v}_t) \colonequals - \langle M_{t-1}\bold{k}_t, \bold{v}_t \rangle$ 로 두고 경사 하강법으로 메모리를 최적화하는 것을 목표로 한다면, 메모리 업데이트 규칙은 다음과 같다: (여기서 $\nabla \tilde{L}(M_{t-1};\bold{k}_t,\bold{v}_t)=\bold{v}_t\bold{k}_t^T$ 이고 학습률 $\eta_t=1$ 로 둔다).

M_{t+1}=\argmin_M \langle M\bold{k}_{t+1},\bold{v}_{t+1} \rangle + \| M-M_{t} \|^2_2~~~~\text{with gradient descent},~~~~(15)\\ \rArr~M_{t+1}=M_t - \nabla \tilde{L}(M_t;\bold{k}_{t+1},\bold{v}_{t+1})=M_t+\bold{v}_{t+1}\bold{k}_{t+1}^T,~~~~(16)

이는 식 13의 정규화되지 않은 선형 어테션의 업데이트 규칙과 동일하다. 또한, 첫 번째 예시에서 관찰했듯이, 경사 하강법으로 선형 계층을 훈련하는 것은 연합 메모리의 1-계층 최적화 문제이며(식 3 참조), 따라서 투영 계층( $W_{\bold{k}}, W_{\bold{v}}, W_{\bold{q}}$ )의 일반적인 훈련/업데이트 과정 자체가 연합 메모리의 최적화 과정이다. 따라서, 이 설정, 즉 경사 하강법으로 선형 어텐션을 훈련하는 것은 2단계 최적화 과정으로 볼 수 있으며, 여기서 외부 루프(훈련 과정이라고도 함)는 경사 하강법으로 투영 계층을 최적화하는 반면, 내부 루프는 경사 하강법으로 $M_t$ 의 내부 메모리를 최적화한다.

위에서 논의했듯이, 여기서는 두 개의 연합 메모리가 있으므로, 각각 자체적인 최적화 과정과 기울기 흐름을 갖는다는 점에 유의해야 한다. 즉, 외부 레벨 매개변수 $W_{\bold{k}}, W_{\bold{v}}, W_{\bold{q}}$ 의 최적화에서는 매개변수 $M(\cdot)$ 에 대한 기울기가 없으므로, 이를 통한 역전파는 없다. 유사하게, 내부 레벨에서는 투영 계층을 통한 역전파가 없으며, 이들은 고정된 것으로 간주된다. 더욱이, 이 예시에서 위의 공식화는 선형 어텐션의 FWPs 관점과도 밀접하게 연결된다는 점에 주목해야 하며, 여기서 투영은 느린 가중치로 간주되고 식 13의 메모리 업데이트는 빠른 가중치 업데이트 규칙이다.

Architectural Decomposition with More Levels. 위의 두 예시 모두에서, 우리는 2단계 최적화 과정으로 변환될 수 있는 간단한 사례들을 논의했으며, 이는 또한 FWPs 해석과도 일치한다. 그러나 실제로는 모델을 훈련하기 위해 더 강력한 최적화 알고리즘을 사용해야 하거나, 메모리를 위해 더 강력한 순환 업데이트 규칙을 사용해야 한다. 간단한 예로, 모멘텀을 사용한 경사 하강법을 사용하여 선형 어텐션 모델을 훈련한다고 가정한다. 위의 예시들에서, 우리는 선형 어텐션 구성 요소가 두 개의 중첩된 최적화 문제로 어떻게 분해될 수 있는지 보여준다. 유사하게, 여기서 모델은 2단계 최적화 문제로 표현될 수 있으며, (1) 내부 레벨은 경사 하강법을 사용하여 컨텍스트를 압축하도록 메모리를 최적화하고(식 15 참조), (2) 외부 레벨은 모멘텀을 사용한 경사 하강법으로 투영 계층을 최적화한다. 흥미롭게도, 첫 번째 예시로부터, "모멘텀을 사용한 경사 하강법" 알고리즘 자체가 실제로 모멘텀 항이 과거의 기울기를 자신의 매개변수로 압축하는 연합 메모리인 2단계 최적화 문제임을 알고 있다.

2.2 Nested Optimization Problems

이전 섹션에서, 우리는 기계 학습 모델을 일련의 중첩되거나 다단계의 최적화 문제들로 분해하는 방법에 대한 예시들을 제공한다. 다음으로, 우리는 먼저 중첩 학습 문제에 대한 공식적인 정식화를 제시하고, 그 후 데이터로부터 학습하는 통합 계산 시스템인 신경 학습 모듈(Neural Learning Module)을 정의하는 것을 목표로 한다.

이전 섹션에서 관찰했듯이, 우리는 모델을 일련의 최적화 과정으로 분해했지만, 이러한 문제들에 대한 계층(또는 순서)을 정의하고 이 형식으로 모델을 고유하게 표현할 수 있는지 여부는 여전히 불분명하다. 섹션 1에서 논의된, 각 부분의 정보 처리 주파수 속도를 나타내는 뇌파의 계층 구조에서 영감을 받아, 우리는 각 최적화 문제의 업데이트 속도를 사용하여 구성 요소를 여러 수준으로 정렬한다. 이를 위해, 우리는 하나의 데이터 포인트에 대한 하나의 업데이트 단계를 시간의 단위로 두고, 각 구성 요소의 업데이트 주파수 속도를 다음과 같이 정의한다.

Definition 2 (Update Frequency). $A$ 의 임의의 구성 요소(예: 운동량 기반 경사 하강법에서의 학습 가능한 가중치 또는 모멘텀 항과 같은 매개변수 구성 요소, 또는 어텐션 블록과 같은 비매개변수 구성 요소일 수 있음)에 대해, 우리는 그 주파수( $f_A$ 로 표기됨)를 시간 단위당 업데이트 횟수로 정의한다.

위 업데이트 주파수가 주어지면, 우리는 연산자 $(\cdot \succ \cdot)$ 에 기반하여 기계 학습 알고리즘의 구성 요소들을 정렬할 수 있다. 우리는 다음의 경우 $A$ 가 $B$ 보다 빠르다고 하고 $A \succ B$ 로 표기한다: (1) $f_A > f_B$ 인 경우, 또는 $f_A = f_B$ 이지만 시간 $t$ 에서의 $B$ 의 상태 계산이 시간 $t$ 에서의 $A$ 의 상태 계산을 요구하는 경우이다. 이 정의에서, $A \nsucc B$ 이고 $B \nsucc A$ 일 때, 우리는 $A \stackrel{f}{=} B$ 로 두는데, 이는 $A$ 와 $B$ 가 동일한 주파수 업데이트를 가지지만, 그 계산이 서로 독립적임을 나타낸다 (나중에, 우리는 AdamW 옵티마이저에서 이 경우의 예시를 제공한다). 위 연산자를 기반으로, 우리는 구성 요소들을 정렬된 "레벨" 세트로 분류하며, 여기서 (1) 같은 레벨의 구성 요소들은 동일한 주파수 업데이트를 가지고, (2) 레벨이 높을수록 주파수는 낮아진다. 특히, 위의 정의에 기반하여, 각 구성 요소는 고유한 최적화 문제와 컨텍스트를 갖는다. 우리가 경사 기반 옵티마이저로 구성 요소의 내부 목적 함수를 최적화하는 동안에도, 위의 진술은 모델의 각 구성 요소에 대해 배타적인 기울기 흐름을 갖는 것과 동일하다. 그러나 일반적인 경우, 비매개변수 해법을 사용할 수 있다 (이에 대해서는 나중에 어텐션에 대해 논의한다).

Neural Learning Module. 중첩 학습 문제에 대한 위의 정의가 주어지면, 우리는 신경 학습 모듈을 기계 학습 모델을 상호 연결된 구성 요소 시스템으로 보여주는 새로운 표현 방식으로 정의하며, 각 구성 요소는 고유한 기울기 흐름을 갖는다. 딥 러닝과는 직교적으로, 중첩 학습은 더 많은 레벨을 가진 신경 학습 모델을 정의할 수 있게 하여, 더욱 표현력이 풍부한 아키텍처를 초래한다는 점에 주목한다.

중첩 학습은 여러 (다층) 레벨로 구성된 계산 모델이 서로 다른 수준의 추상화 및 시간 규모로 데이터로부터 학습하고 데이터를 처리할 수 있도록 허용한다.

다음으로, 우리는 중첩 학습 관점에서 옵티마이저와 잘 알려진 딥 러닝 아키텍처를 연구하고, 중첩 학습이 이러한 구성 요소들을 향상시키는 데 어떻게 도움을 줄 수 있는지에 대한 예시들을 제공한다.

2.3 Optimizers as Learning Modules

이 섹션에서, 우리는 잘 알려진 옵티마이저와 그 변형들이 어떻게 중첩 학습의 특별한 인스턴스인지 이해하는 것으로 시작한다. 모멘텀을 사용한 경사 하강법을 상기하면 다음과 같다:

W_{i+1}=W_i + \bold{m}_{i+1}\\ \bold{m}_{i+1}=\alpha_{i+1}\bold{m}_i - \eta_t \nabla L(W_i;x_i),~~~~(17)

여기서 행렬(또는 벡터) $\bold{m}_i$ 는 상태 $i$ 에서의 모멘텀이며, $\alpha_i$ 와 $\eta_i$ 는 각각 적응형 학습률과 모멘텀 비율이다. $\alpha_{i+1}=1$ 이라고 가정하면, 모멘텀 항은 경사 하강법을 사용하여 다음 목적 함수를 최적화한 결과로 간주될 수 있다:

\min_\bold{m} \langle\bold{m}\nabla L(W_i;x_i)^T, \bold{I} \rangle. ~~~~(18)

이 해석은 모멘텀이 실제로 목적 함수의 기울기를 자신의 매개변수에 암기하는 방법을 학습하는 메타 메모리 모듈로 간주될 수 있음을 보여준다. 이러한 직관을 바탕으로, 부록 C.4에서는 Adam이 약간의 수정만으로 모델 기울기에 대한 최적의 연합 메모리임을 보여준다. 다음으로, 이 관점이 어떻게 더 표현력이 풍부한 옵티마이저를 설계하는 결과를 가져올 수 있는지 보여준다.

Extension: More Expressive Association. 앞서 논의했듯이, 모멘텀은 값(value)이 없는 연합 메모리이므로 표현력이 제한된다. 이 문제를 해결하기 위해, 연합 메모리의 원래 정의(즉, 키를 값으로 매핑하는 것)를 따라, 우리는 값 매개변수를 $v_i=P_i$ 로 두고, 모멘텀은 다음을 최소화하는 것을 목표로 한다:

\min_\bold{m} \langle\bold{m}\nabla L(W_i;x_i)^T, \bold{P}_i \rangle,~~~~(19)

경사 하강법을 사용하여 이를 최소화하면, 다음과 같은 업데이트 규칙이 발생한다:

W_{i+1}=W_i+\bold{m}_{i+1}\\ \bold{m}_{i+1}=\alpha_{i+1}\bold{m}_i-\eta_t\bold{P}_i\nabla L(W_i;x_i).~~~~(20)

이 공식화는 모멘텀 GD에 선행 조건화(preconditioning)을 사용하는 것과 동일하다. 사실상, 선행 조건화는 모멘텀 항이 $P_i$ 와 기울기 항 $\nabla L(W_i;x_i)$ 사이의 매핑을 압축하는 방법을 학습하는 연합 메모리임을 의미한다. 선행 조건화의 합리적인 선택(예: 랜덤 특징)은 모멘텀을 가진 GD의 초기 버전(그 자체로 값 없는 메모리, 즉 모든 기울기를 단일 값으로 매핑함)의 표현력을 향상시킬 수 있지만, 위의 관점은 어떤 선행 조건화가 더 유용한지에 대한 더 많은 직관을 제공한다. 즉, 모멘텀은 기울기를 해당 값으로 매핑하는 것을 목표로 하는 메모리 역할을 하며, 따라서 기울기의 함수(예: 헤시안(Hessian)에 대한 정보)는 메모리에 더 의미 있는 매핑을 제공할 수 있다.

Extension: More Expressive Objectives. Behrouz 등의 논의에 따르면, 내적 유사성(dot-product similarity)의 내부 목적 함수를 최적화하는 것은 헤비안(Hebbian)과 유사한 업데이트 규칙을 초래하며, 이는 메모리의 효율성을 떨어뜨릴 수 있다. 이 내부 목적 함수의 자연스러운 확장으로, $l_2(\cdot)$ 회귀 손실을 사용하여 (해당 키-값 매핑 적합도를 측정하기 위해) 손실 함수 $\|\bold{m}\nabla L(W_i;x_i)^T-\bold{P}_i \|^2_2$ 를 최소화할 수 있으며, 그 결과 다음과 같은 업데이트 규칙이 발생한다:

W_{i+1}=W_i+\bold{m}_{i+1},~~~~(21)\\ \bold{m}_{i+1}=(\alpha_{i+1}\bold{I}-\nabla L(W_i;x_i)^T\nabla L(W_i;x_i))\bold{m}_i - \eta_t\bold{P}_i\nabla L(W_i;x_i), ~~~~(22)

이 업데이트는 델타 규칙에 기반하며, 따라서 메모리(모멘텀)가 제한된 용량을 더 잘 관리하고 과거 기울기의 계열을 더 잘 암기하도록 허용한다.

Extension: More Expressive Memory. 앞서 논의했듯이, 모멘텀은 선형 계층(즉, 행렬 값)을 사용하여 과거 기울기 값을 압축하는 메타 메모리 모델로 간주될 수 있다. 모멘텀의 선형적 특성 때문에, 내부 목적 함수에 의해 학습될 수 있는 것은 과거 기울기의 선형 함수뿐이다. 이 모듈의 학습 용량을 증가시키기 위한 한 가지 대안은 대체 강력한 지속성 학습 모듈을 사용하는 것, 즉 모멘텀을 위한 선형 행렬 값 메모리를 MLP로 대체하는 것이다. 따라서 과거 기울기에 대한 메모리로서의 모멘텀은 기울기의 근본적인 역학을 포착할 수 있는 더 많은 용량을 가진다. 이를 위해, 우리는 식 17의 공식화를 다음과 같이 확장한다:

W_{i+1}=W_i+\bold{m}_{i+1}(\bold{u}_i),~~~~\text{and}~~~~\bold{m}_{i+1}=\alpha_{i+1}\bold{m}_i-\eta_t\nabla L^{(2)}(\bold{m}_i;\bold{u}_i, \bold{I}),~~~~(23)

여기서 $u_i=\nabla L(W_i;x_i)$ 이고 $\nabla L^{(2)}(\cdot)$ 은 모멘텀의 내부 목적 함수이다 (예: dot product similarity $\langle \bold{m}(\bold{u}_i^T),1 \rangle)$ . 우리는 이 변형을 심층 모멘텀 경사 하강법(Deep Momentum Gradient Descent, DMGD)이라고 부른다.

Extension: None Linear Outputs. 모멘텀을 신경 아키텍처로 보는 위의 관점을 바탕으로, 모멘텀 메모리 모듈의 표현력을 향상시키기 위한 일반적인 기술 중 하나는 그 출력 위에 비선형성을 사용하는 것이다. 즉, 우리는 식 23을 다음과 같이 재구성한다:

W_{i+1}=W_i+\sigma(\bold{m}_{i+1}(\bold{u}_i)),~~~~\text{and}~~~~\bold{m}_{i+1}=\alpha_{i+1}\bold{m}_i-\eta_t \nabla L^{(2)}(\bold{m}_i;\bold{u}_i, \bold{I}), ~~~~(24)

여기서 $\sigma(\cdot)$ 는 임의의 비선형성이다. 예를 들어, $\sigma(\cdot)=\text{Newton-Schulz}(\cdot)$ 이고, 여기서 $\text{Newton-Schulz}(\cdot)$ 는 반복적인 Newton-Schulz 방법이며, $m(\cdot)$ 이 선형 계층이라고 가정한다면, 결과 옵티마이저는 Muon 옵티마이저와 동일하다.

Going Beyond Simple Backpropagation. 앞서 2.1절에서 논의했듯이, 사전 훈련 과정과 역전파는 입력 데이터가 예측된 출력 $\nabla_{y_t}L(W_t;x_t)$ 에 의해 야기된 놀람 신호로 매핑되는 연합 메모리의 한 형태이다:

W_{t+1}=W_t-\eta_{t+1}\nabla L(W_t;x_t)=W_t-\eta_{t+1}\nabla_{y_t}L(W_t;x_t) \otimes x_t, ~~~~\text{where}~x_t \sim D_{\text{train}}, ~~~~(25)

이는 연합 메모리 관점에서 다음 최적화 과정의 경사 하강법 한 단계와 동일하다:

\min_W~ \langle Wx_t, \nabla_{y_t}L(W_t;x_t) \rangle.~~~~(26)

부록 C에서 논의했듯이, 위의 공식화는 $x_t$ 와 같은 데이터 샘플 간의 의존성을 무시하게 만든다. 이를 데이터 포인트의 의존성(토큰 공간에서 옵티마이저를 사용할 때 매우 중요함)도 고려하는 더 강력한 공식화로 확장하기 위해, $l_2$ 회귀 목적 함수를 경사 하강법의 한 단계와 함께 다음과 같이 사용한다:

\min_W \| Wx_t-\nabla_{y_t}L(W_t;x_t) \|^2_2.~~~~(27)

이 공식화는 경사 하강법의 새로운 변형을 초래하며, 이는 다음과 같이 단순화될 수 있다:

W_{t+1}=W_t(\bold{I}-x_tx_t^T)-\eta_{t+1}\nabla_{W_t}L(W_t;x_t)~~~~(28)\\ =W_t(\bold{I}-x_tx_t^T)-\eta_{t+1} \nabla_{y_t}L(W_t;x_t) \otimes x_t, ~~~~\text{where} x_t \sim D_{\text{train}},~~~~(29)

후에, 우리는 이 옵티마이저를 우리의 HOPE 아키텍처의 내부 옵티마이저로 사용한다.

3. HOPE: A Self-Referential Learning Module with Continuum Memory

기존의 아키텍처 백본은 (1) 시퀀스 길이에 걸쳐 정보를 활발하게 융합하는 역할을 하는 작업 기억 모듈(예: 어텐션), 그리고 (2) 특징에 걸쳐 정보를 융합하고 사전 훈련 단계의 영속적인 기억 또는 지식 저장소 역할을 하는 피드포워드 계층(예: MLP)으로 구성된다. NL 관점에서, 사전 훈련은 학습 모듈의 가장 바깥쪽 레벨이 제한된 컨텍스트 흐름에 걸쳐 업데이트되는 단계이다. 따라서 지속 학습 설정에서, 이러한 사전 훈련 단계 또한 시간이 지남에 따라 거의 업데이트되지 않으며, 그에 해당하는 지식 저장소도 시간이 지남에 따라 거의 업데이트될 필요가 있다. 이러한 직관을 바탕으로, 우리는 장기/단기 기억 시스템의 전통적인 관점을 확장하고 각 레벨(주파수 도메인)에 대한 지식 저장 피드포워드를 제안한다.

주파수의 정의가 주어지면, 연속체 메모리 시스템(Continuum Memory System, CMS)은 일련의 MLP 블록 $\text{MLP}^{(f_1)}(\cdot), …, \text{MLP}^{(f_k)}(\cdot)$ 으로 공식화되며, 각 블록은 청크 크기 $C^{(l)} \colonequals \frac{\max_lC^{(l)}}{f_l}$ 와 연관되며, 입력 $x=\{x_, …, x_T\}$ 가 주어지면 사슬의 출력은 다음과 같이 계산된다 (명확성을 위해 정규화는 생략한다):

y_t=\text{MLP}^{(f_k)}(\text{MLP}^{(f_{k-1})}(\cdot\cdot\cdot\text{MLP}^{(f_1)}(x_t))),~~~~(30)

여기서 $l$ -번째 MLP 블록의 매개변수, 즉 $\theta^{(f_l)}$ 는 $C^{(l)}$ 단계마다 업데이트 된다:

\theta^{(f_l)}_{i+1}=\theta^{f_l}_{i}-\begin{cases} \sum^i_{t=i-C^{(l)}}\eta_t^{(l)}f(\theta_t^{(f_l)};x_t) & \text{if}~i \equiv0 ~(\text{mod}~ C^{(l)}),\\ 0&\text{otherwise.} \end{cases}~~~~(31)

부록 B.1에서, 우리는 완전히 중첩된 MLP 계층을 포함하여 이 공식화의 다양한 변형에 대해 논의한다. 여기서 $\eta_t^{(l)}$ 는 $\theta_t^{(f_l)}$ 에 해당하는 학습률이며, $f(\cdot)$ 는 임의의 옵티마이저의 오차 구성 요소이다 (예: 경사 하강법에서의 $\nabla L(\theta^{(f_l)}_t;x_t))$ . 기존의 트랜스포머 블록은 $k=1$ 인 이 공식화의 특별한 인스턴스이다. 식 31은 중요한 해석을 제공하는데, 매개변수 $\theta^{(f_l)}_t$ 는 자신의 컨텍스트를 자신의 매개변수로 압축하는 역할을 하며, 따라서 그 컨텍스트의 추상적 지식의 대표자가 된다는 점이다.

HOPE. 우리는 Titans와 부록 B.1에 있는 리의 경사 하강법 변형을 기반으로 하는 자기 참조 학습 모듈을 추가로 제시한다. 이 자기 참조 시퀀스 모델을 연속체 메모리 시스템과 결합하면 HOPE 아키텍처가 탄생한다.

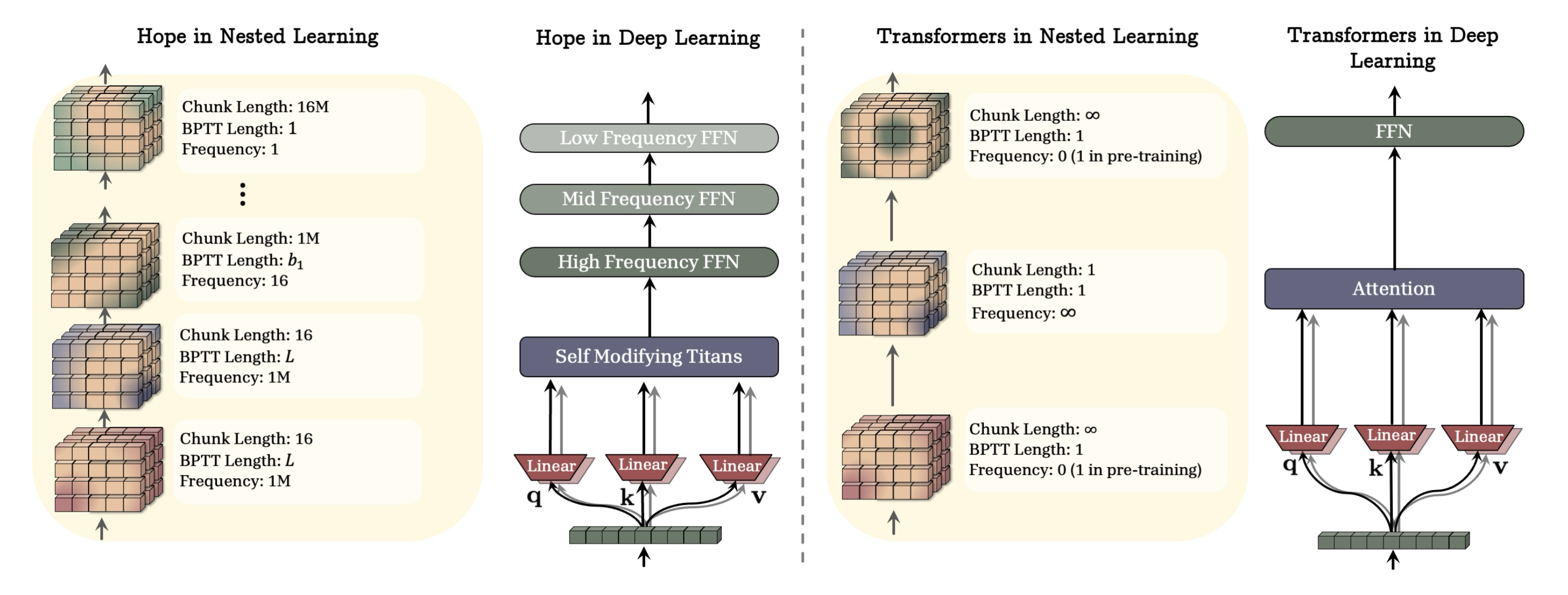
그림 3은 HOPE 아키텍처 백본과 Transformer의 비교를 보여준다 (명확성을 위해 정규화 및 잠재적인 데이터 종속 구성 요소는 제거한다).

Figure 3: 그림 3은 HOPE 아키텍처 백본과 Transformer의 비교를 보여준다 (명확성을 위해 정규화 및 잠재적인 데이터 종속 구성 요소는 제거한다).

Table 1

4. Experiments

지면 제약으로 인해, 본 논문에서는 HOPE의 언어 모델링 및 상식 추론 작업에 대한 평가 결과를 본문에 보고한다. 그러나 옵티마이저에 대한 실험, 인컨텍스트 학습의 출현, HOPE의 지속 학습 능력, 절제 연구(ablation studies), 장문 컨텍스트 작업 등을 포함한 광범위한 결과 세트는 부록에서 보고한다. 실험 설정 및 사용된 다른 데이터 세트에 대한 세부 정보는 부록 G에 있다.

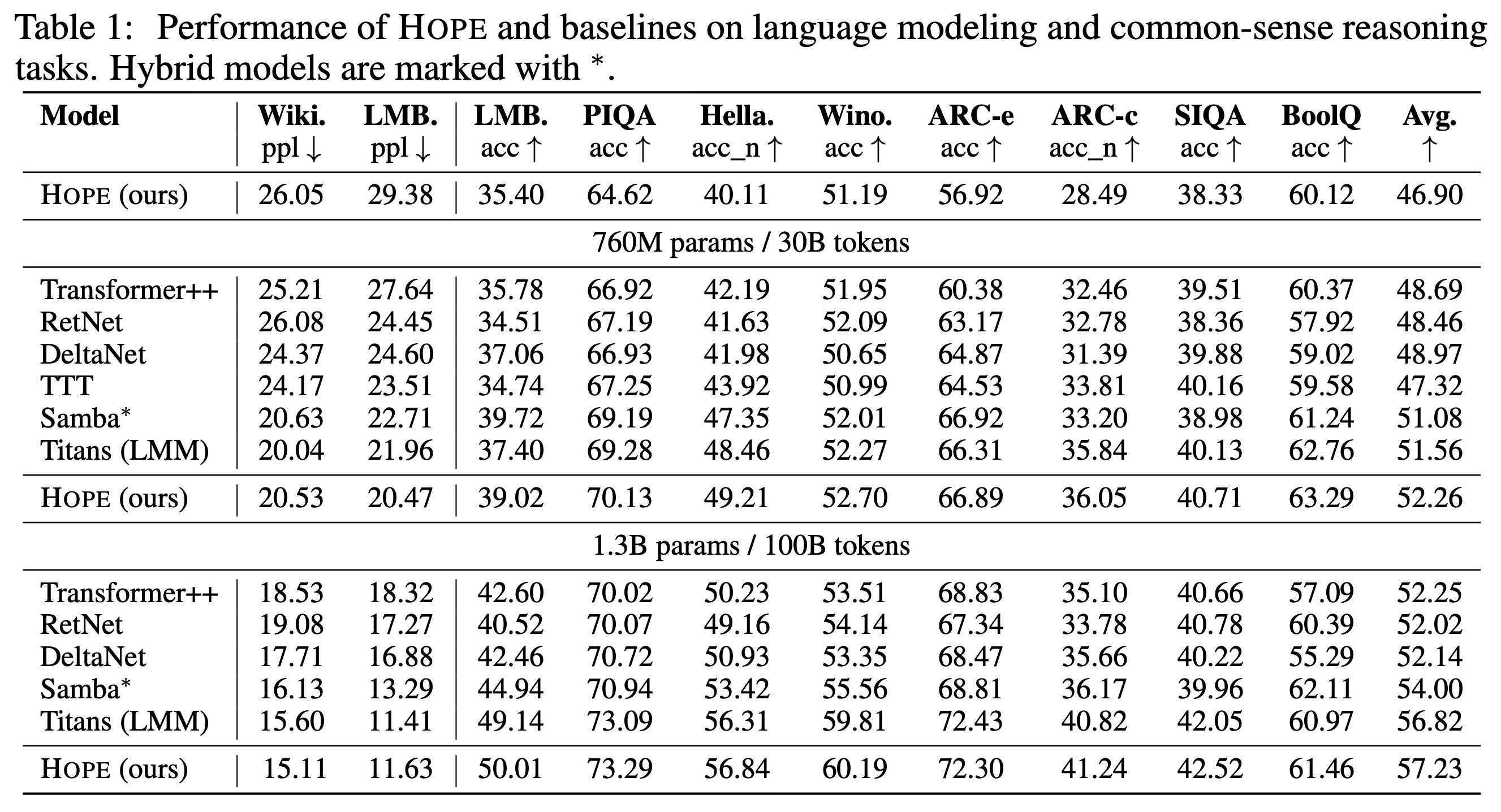
Language Modeling and Common-sense Reasoning. 우리는 최근의 시퀀스 모델링 연구를 따라 HOPE와 3억 4천만 개(340M), 7억 6천만 개(760M), 13억 개(1.3B) 크기의 기준선(baselines) 모델에 대한 언어 모델링 및 상식 추론 다운스트림 작업 결과를 보고한다. 이 결과들은 표 1에 보고된다. HOPE는 모든 규모와 벤치마크 작업에서 매우 우수한 성능을 보여주며, Transformer와 Gated DeltaNet, Titans를 포함한 최근의 현대적인 순환 신경망 모두를 능가한다. HOPE를 Titans 및 Gated DeltaNet과 비교할 때, 컨텍스트에 기반하여 키, 값, 쿼리 투영을 동적으로 변경하는 것과 심층 메모리 모듈이 벤치마크 결과에서 더 낮은 퍼플렉시티(perplexity)와 더 높은 정확도를 가진 모델을 초래할 수 있음을 확인한다.

5. Conclusion

중첩 학습 패러다임은 딥러닝에 대한 우리의 이해가 한 단계 진보했음을 의미한다. 아키텍처와 최적화를 중첩된 최적화 문제들로 구성된 하나의 일관된 시스템으로 다룸으로써, 우리는 여러 단계를 쌓아 올리는 새로운 설계의 차원을 열었다. Hope 아키텍처와 같이 그 결과로 탄생한 모델들은, 이러한 요소들을 통합하는 원칙적인 접근법이 더욱 표현력이 풍부하고 유능하며 효율적인 학습 알고리즘으로 이어질 수 있음을 보여준다. 우리는 중첩 학습 패러다임이 한계가 있고 망각하기 쉬운 현재 LLM의 특성과 인간 뇌의 놀라운 지속적 학습 능력 사이의 격차를 해소하는 데 견고한 기반을 제공한다고 믿는다. 연구 커뮤니티가 이 새로운 영역을 탐구하고, 차세대 자기 개선(self-improving) AI를 구축하는 여정에 함께하기를 기대한다.