그래프: 위상 정렬

위상 정렬

위상정렬은 정렬 알고리즘의 일종이다. 이는 순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘이다. 조금더 구체적으로 위상 정렬은 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것이다. 예시로는 선수과목이 있다. 자료구조 과목을 수강한뒤에 알고리즘 과목을 수강하는 것이 권장된다면, 위상 정렬을 수행하여 모든 선후 관계를 지키는 전체 순서를 게산할 수 있다. 구체적인 동작 과정을 아래와 같다.

1. 진입 차수가 0인 노드를 큐에 넣는다.
2. 큐가 빌 때까지 다음의 과정을 반복한다.

• 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
• 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.

위상 정렬 알고리즘은 큐가 빌때까지 큐에서 원소를 꺼내고 처리하는 과정을 반복한다. 이때 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다.

동작 과정 예시

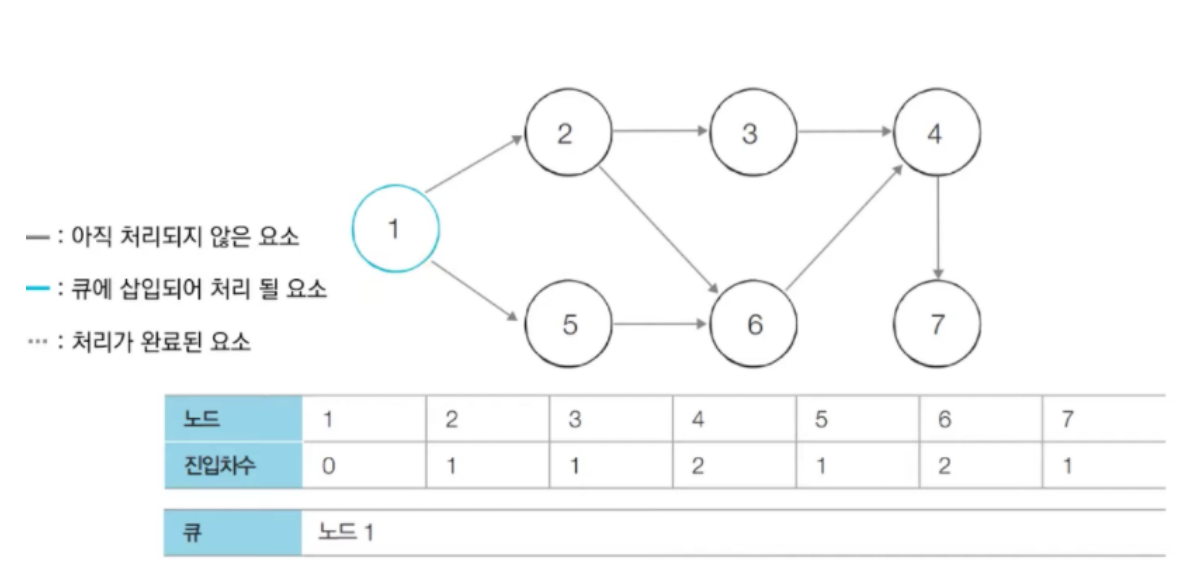
• 초기에는 진입 차수가 0인 노드를 큐에 넣는다. 따라서 노드1을 큐에 삽입한다.
  
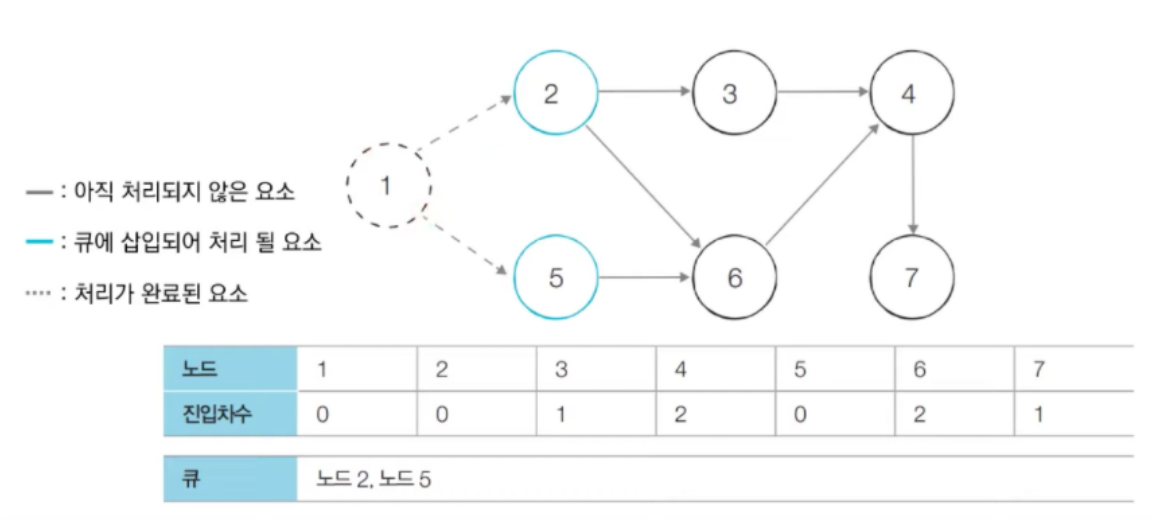
• 먼저 큐에 삽입되어 있는 노드1을 꺼내고, 노드1의 간선을 제거한다.(노드2, 노드5의 진입차수 각각 -1) 그리고 진입차수가 0인 노드2, 노드5를 큐에 삽입한다.
  
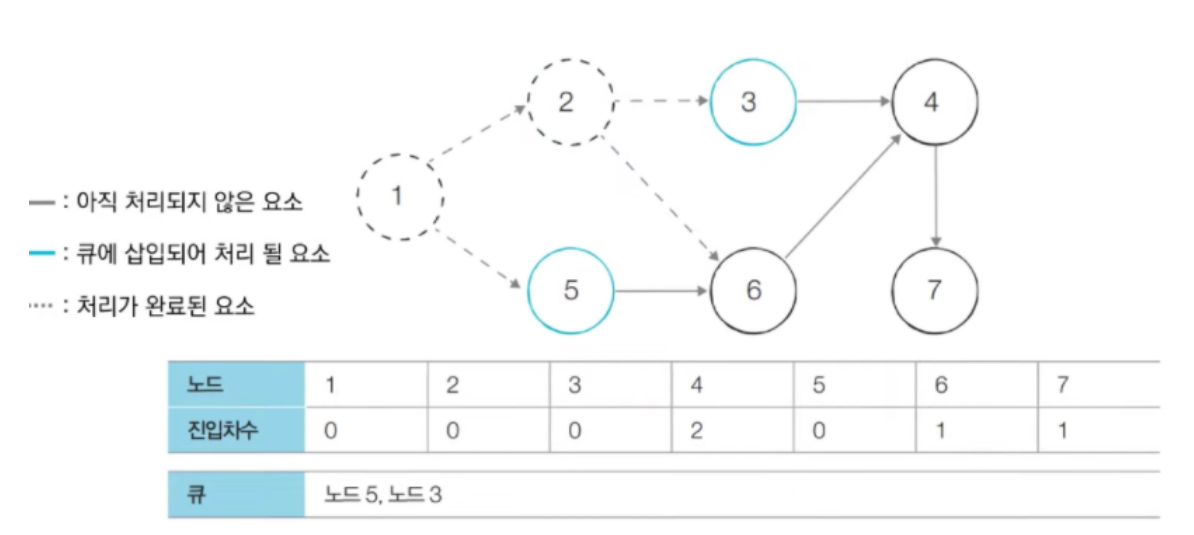
• 다음으로 큐에서 노드 2를 꺼내고, 노드2의 간선을 제거한다. 그러면 노드 3의 진입차수가 0이 되므로 노드3을 큐에 삽입힌다.
  
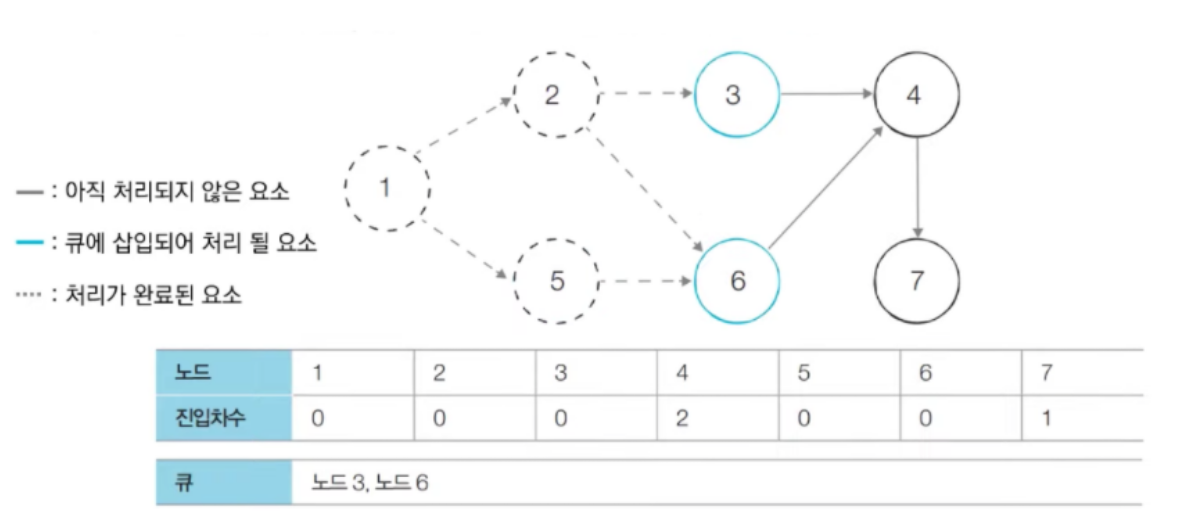
• 다음으로 큐에서 노드5를 꺼내고, 노드5의 간선을 제거한다. 그러면 노드 6의 진입차수가 0이므로 큐에 삽입한다.
  
• 다음으로 큐에서 노드3을 꺼내고, 간선을 제거한다. 이때 노드 4의 진입차수는 아직 0이 아니므로 다음과정을 진행한다.
  
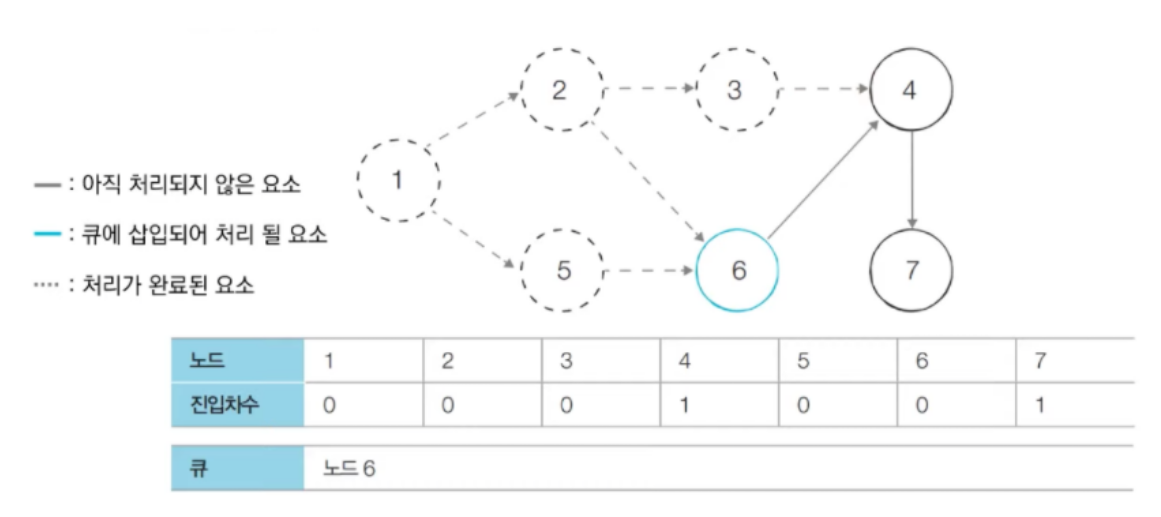
• 다음으로 큐에서 노드 6을 꺼내고 간선을 제거한다. 이때 노드 4의 진입차수가 0이므로 큐에 삽입한다.
  
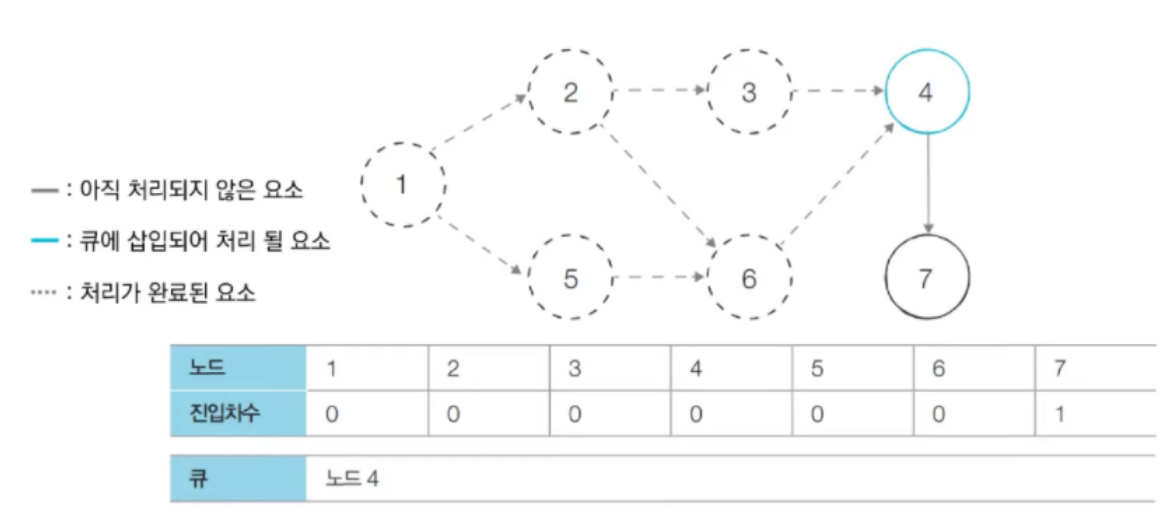
• 큐에서 노드 4를 꺼내고 간선을 제거한다. 그리고 노드 7을 큐에 삽입한다.
  
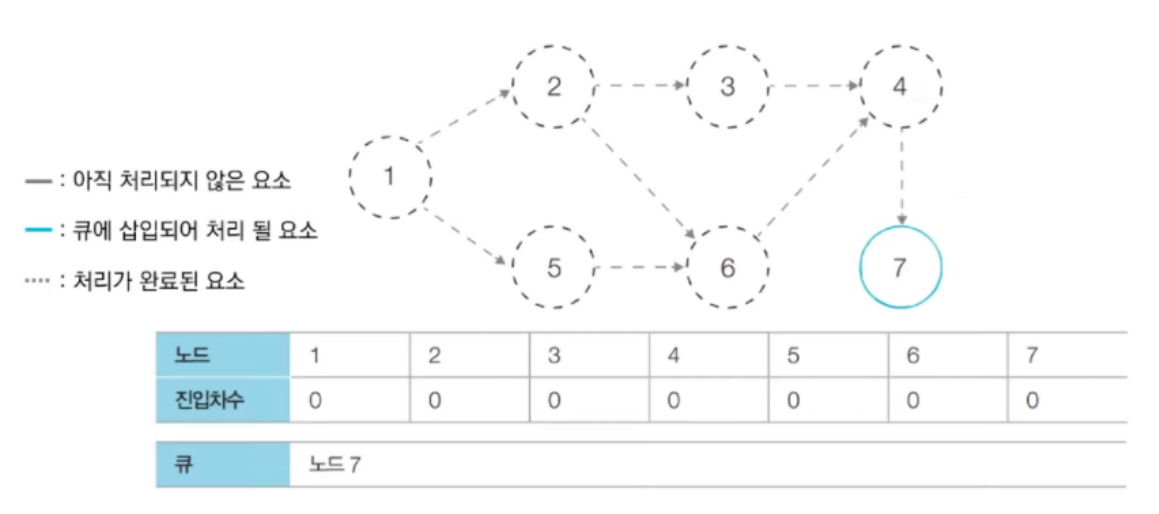
• 마지막으로 큐에서 노드7을 꺼낸다. 이때 다음으로 진입차수가 0이되는 노드가 없기 때문에 넘어간다.
  
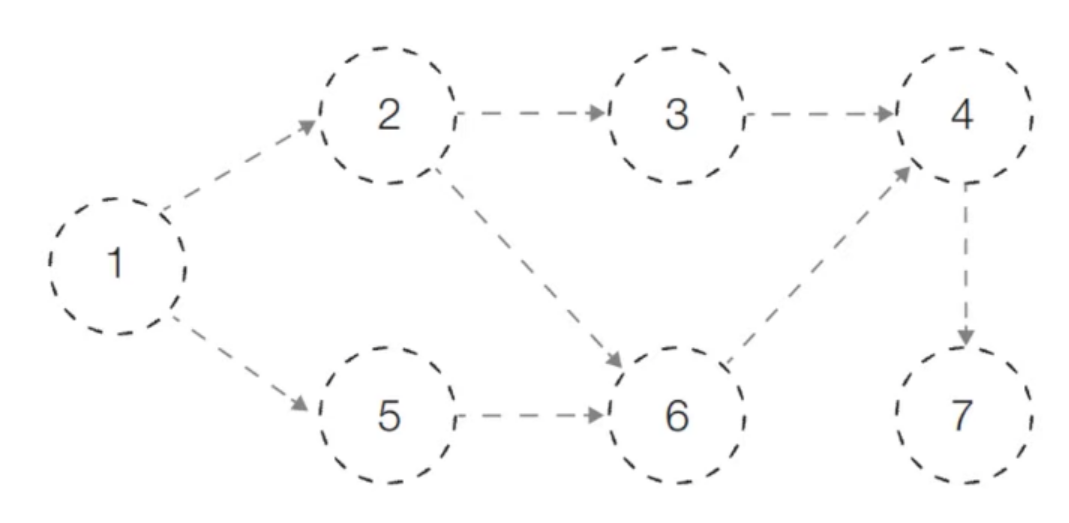
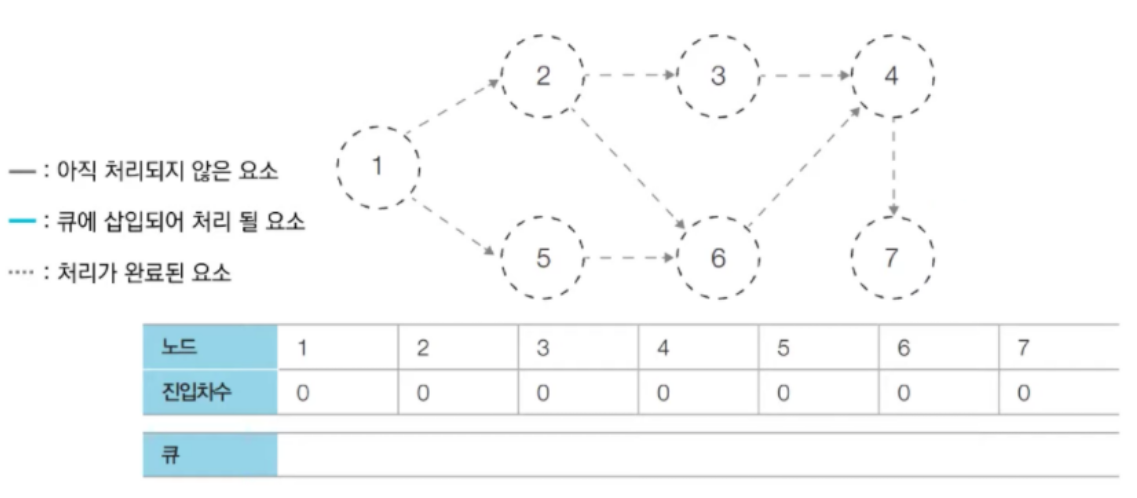
• 결과는 1 - 2 - 5 - 3 - 6 - 4 - 7이 답이 될 수도 있으며, 1 - 5 - 2- 3 - 6 - 4 - 7 이 정답이 될 수도 있다.

위상정렬 소스코드

from collections import deque

#노드의 개수와 간선(union 연산)의 개수 입력 받기
v, e = map(int, input().split())
#모든 노드에 대한 진입차수는 0으로 초기화
indegree = [0] * (v + 1)
#그래프 초기화
graph = [[] for _ in range(v + 1)]

#모든 간선 정보 입력받기
for i in range(e):
    a, b = map(int, input().split())
    graph[a].append(b) #정점 a 에서 b로 이동 가능
    indegree[b] += 1


def topology_sort():
    result = [] #알고리즘 수행 결과를 담을 리스트
    q = deque()

    #처음 시작할 때 진입차수가 0인 노드를 삽입
    for i in range(1, v + 1):
        if indegree[i] == 0:
            q.append(i)

    while q:
        now = q.popleft()
        result.append(now)
        for i in graph[now]:
            indegree[i] -= 1
            #새롭게 진입차수가 0이 되는 노드를 큐에 삽입
            if indegree[i] == 0:
                q.append(i)

    #위상 정렬을 수행한 결과 출력
    for i in result:
        print(i, end=' ')

topology_sort()

• 위상 정렬의 시간복잡도는 O(V + E) 이다. 차례대로 모든 노드를 확인하면서, 해당 노드에서 출발하는 간선을 차례대로 제거해야 한다. 따라서 노드와 간선을 모드 확인한다는 측면에서 O(V + E)의 시간이 소요된다.