서로소 집합 & 사이클 판별 알고리즘

서로소 집합

수학에서 서로소 집합이란 공통 원소가 없는 두 집합을 의미한다. 예를 들어 집합 {1, 2} 와 집합 {2, 3}은 2라는 공통적인 원소가 있기 때문에 서로소 관계가 아니다. 서로소 집합 자료구조란 서로소 부분 집합들로 나누어진 원소드의 데이터를 처리하기 위한 자료구조 라고 할 수 있다. 이 자료구조는 union, find 연산이 가능하다. union 연산은 2개의 원소가 포함된 집합을 하나의 집합으로 합치는 연산이다. find 연산은 특정한 원소가 속한 집합이 어떤 집합인지 알려주는 연산이다.

서로소 집합 알고리즘
1. union 연산을 확인하며, 서로 연결된 두 노드 a, b를 확인한다.

• a와 b의 루트 노드인 a' b' 를 각각 찾는다.
• a'를 b'의 부모 노드로 설정한다. (b'가 a'를 가리키도록 한다. b' > a')

2. 모든 union 연산을 처리할 때까지 1번 연산을 반복한다.

전체 집합이 {1, 2, 3, 4, 5, 6} 이 있고 4개의 union 연산인 union 1, 4 union 2, 3 union 2, 4 union 5, 6 이 있다고 해보자. 그러면 이때 6개의 노드가 있고 4개의 간선이 존재하는 그래프로 바꾸어서 생각할 수 있다.

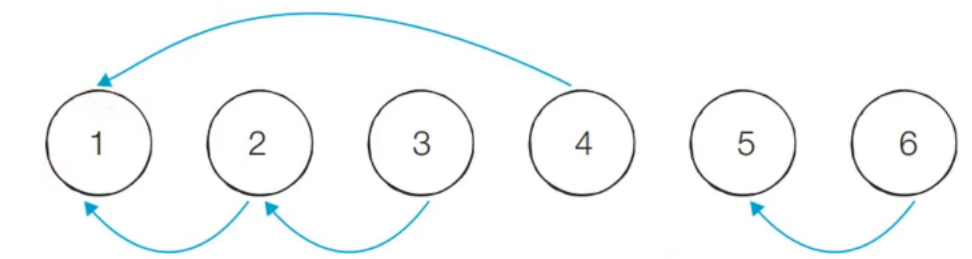
• 위의 그래프에서 루트 노드가 무엇인지에 따라서 각 노드가 어떤 집합에 소속해있는지 알 수 있다. (따라서 서로소 집합 알고리즘에서는 트리 자료구조를 활용)
• 따라서 {1, 2, 3, 4} {5, 6} 2개의 서로소 집합이 있음을 알 수 있다.

동작 과정

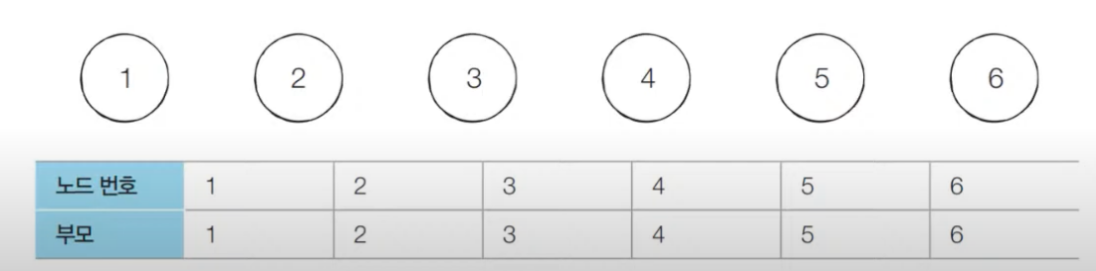
• 초기에는 자기 자신을 부모 노드로 설정한다. 원소의 개수가 6개이므로 6개의 트리가 존재하는 것과 같다.
  
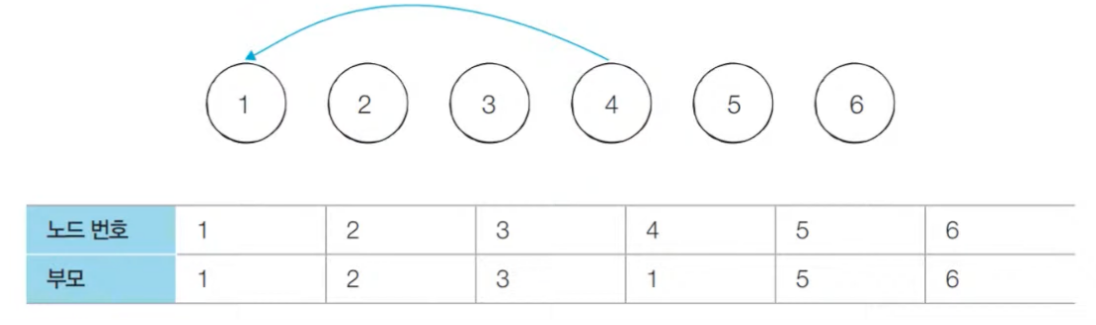
• union 1, 4 연산을 수행함으로써 부모 노드의 숫자가 큰 4의 루트 노드를 1로 설정한다.
  
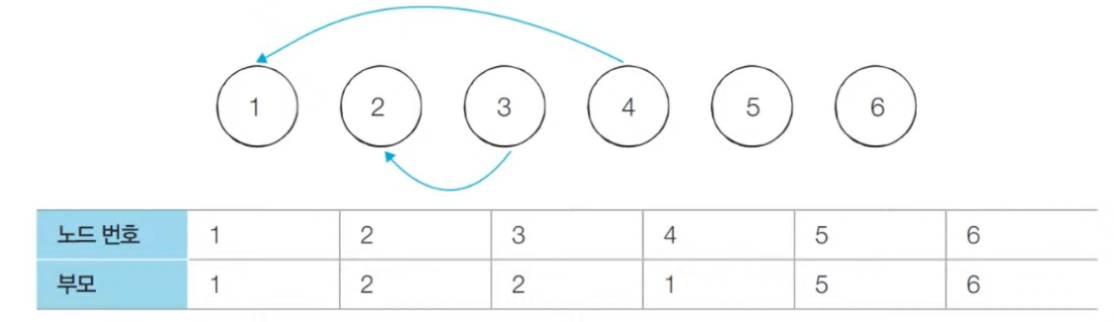
• union 2, 3 연산을 수행함으로써 3의 부모 노드를 2로 설정한다.
  
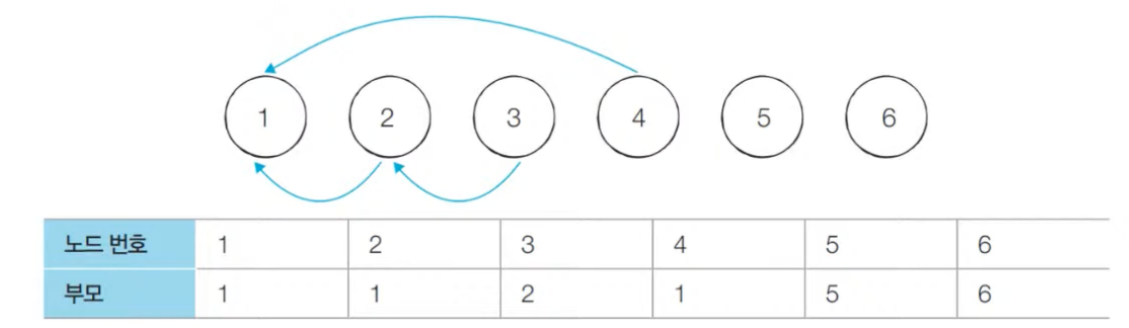
• union 2, 4 연산을 수행함으로써 2의 부모노드가 4의 부모노드보다 크기 때문에 2의 부모노드를 1로 설정한다.
  
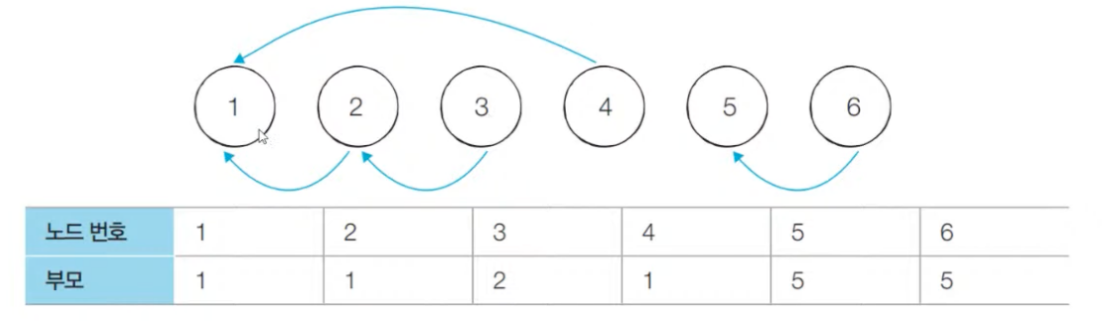
• union 5, 6 마지막 연산을 통해 6의 부모노드를 5로 설정한다.

서로소 집합 알고리즘 소스코드

#특정 원소가 속한 집합을 찾기
def find_parent(parent, x):
    #루트 노드가 아니라면
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]

#두 원소가 속한 집합을 찾기
def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a < b:
        parent[b] = a
    else:
        parent[a] = b

#노드의 개수와 간선(union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) #부모 테이블 초기화

#부모 테이블 상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
    parent[i] = i

#union 연산을 각각 수행
for i in range(e):
    a, b = map(int, input().split())
    union_parent(parent, a, b)

#각 원소가 속한 집합 출력
print('각 원소가 속한 집합: ', end=' ')
for i in range(1, v + 1):
    print(find_parent(parent, i), end=' ')
print()

#부모 테이블 내용 출력
for i in range(1, v + 1):
    print(parent[i], end=' ')

• 노드의 개수가 V개 이고 union 연산이 M번 주어졌을 때 ,시간 복잡도는 O(V + M(1 + log_2-m/v_V)) 이다. 대략 V + Mlog_2_V로 계산하자.

사이클 판별 알고리즘

서로소 집합은 무방향 그래프 내에서의 사이클을 판별할 때 사용할 수 있다.

사이클 판별 알고리즘 과정
1. 각 간선(union 연산) 을 확인하며 두 노드의 루트 노드를 확인한다.

• 루트 노드가 서로 다르다면 두 노드에 대하여 union 연산을 수행한다.
• 루트 노드가 서로 같다면 사이클이 발생한 것이다.

2. 그래프에 포함되어 있는 모든 간선에 대하여 1번 과정을 반복한다.

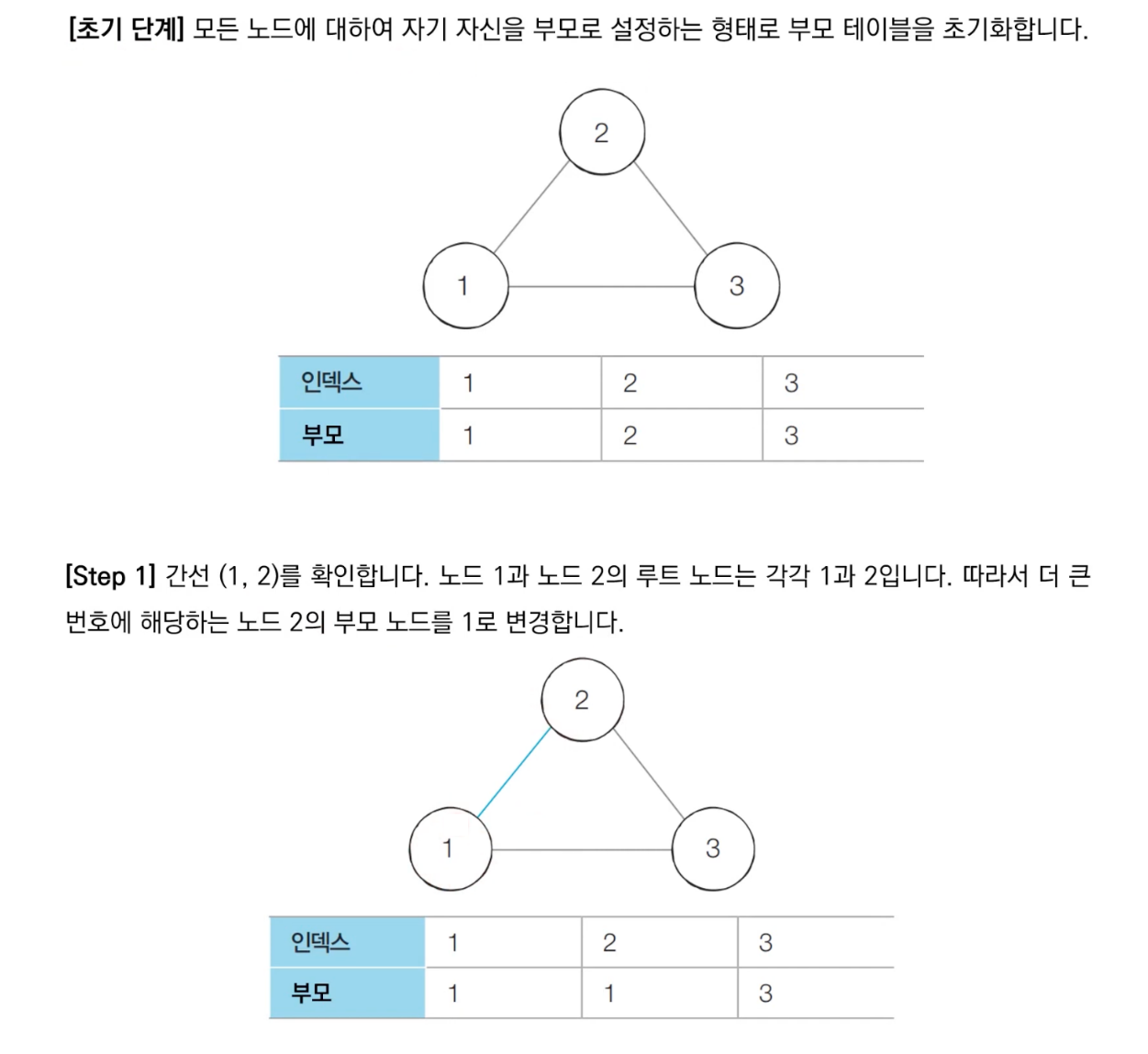
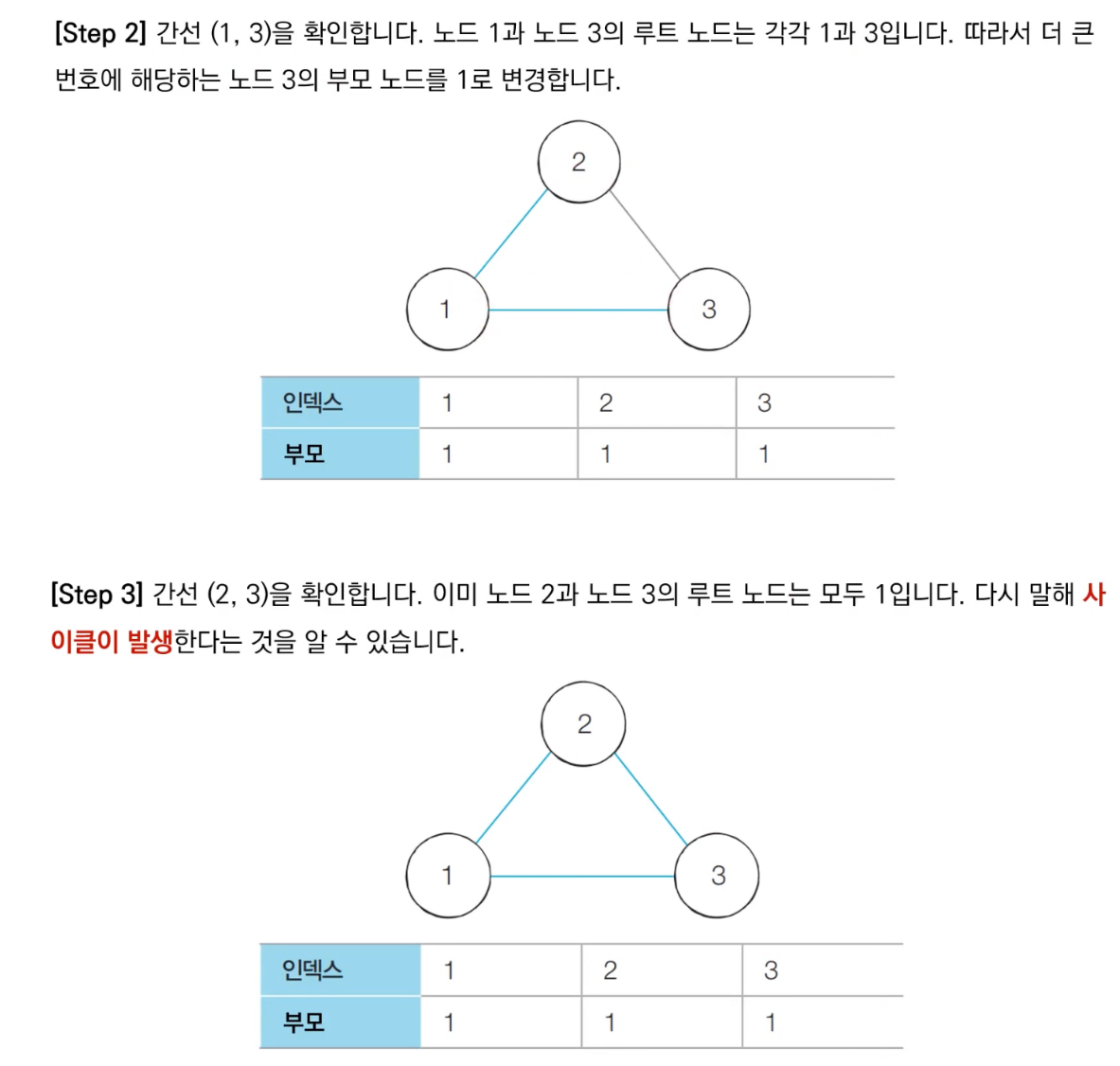
• 사이클 판별 알고리즘은 간선의 개수가 E개일때 모든 간선을 하나씩 확인하며, 매 간선에 대하여 union 및 find 함수를 호출하는 방식으로 동작한다. 그리고 무방향 그래프에서만 적용 가능하다.

사이클 판별 알고리즘 소스코드

def find_parent(parent, x):
    if parent[x] != x:
        parent[x] = find_parent(parent, parent[x])
    return parent[x]

def union_parent(parent, a, b):
    a = find_parent(parent, a)
    b = find_parent(parent, b)
    if a > b:
        parent[a] = b
    else:
        parent[b] = a

#노드의 개수와 간선(union 연산)의 개수 입력 받기
v, e = map(int, input().split())
parent = [0] * (v + 1) #부모 테이블 초기화

#부모 테이블 상에서, 부모를 자기 자신으로 초기화
for i in range(1, v + 1):
    parent[i] = i

cycle = False
#union 연산을 각각 수행
for i in range(e):
    a, b = map(int, input().split())
    #사이클이 발생한 경우
    if find_parent(parent, a) == find_parent(parent, b):
        cycle = True
        break
    else:
        union_parent(parent, a ,b)

if cycle:
    print("사이클이 발생하였습니다")
else:
    print("사이클이 발생하지 않았습니다")