Node Embeddings
Input Graph → Sturucture Features → Learning Algorithm → Prediction
by "Representiation Learning" (feature eng.를 대체하도록)
Graph Representation Learning
- Goal : Efficient task-independent feature learning for machine learning with graphs!
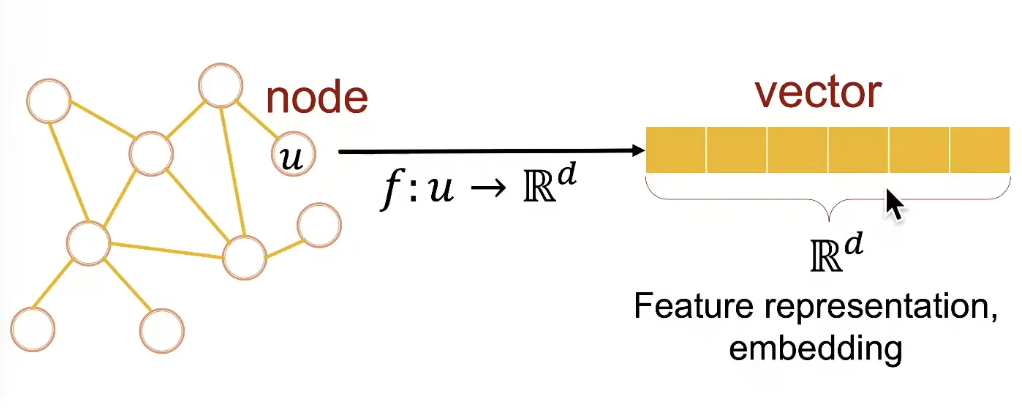
- Mapping을 자동적으로 일어나게 하는것, 안에 들어있는 정보들을 모두 표현할 수 있도록 하는 것
Why Embedding?
- Task: map nodes into an embedding space
❍ Similarity of embeddings between nodes indicates their similarity in the network.
❍ Encode network information
❍ Potentially used for many downstream predictions
Encoder and Decoder
Graph → Adjacency matrix
- Goal is to encode nodes so that similarity in the embedding space (e.g., dot product) approximates similarity in the graph
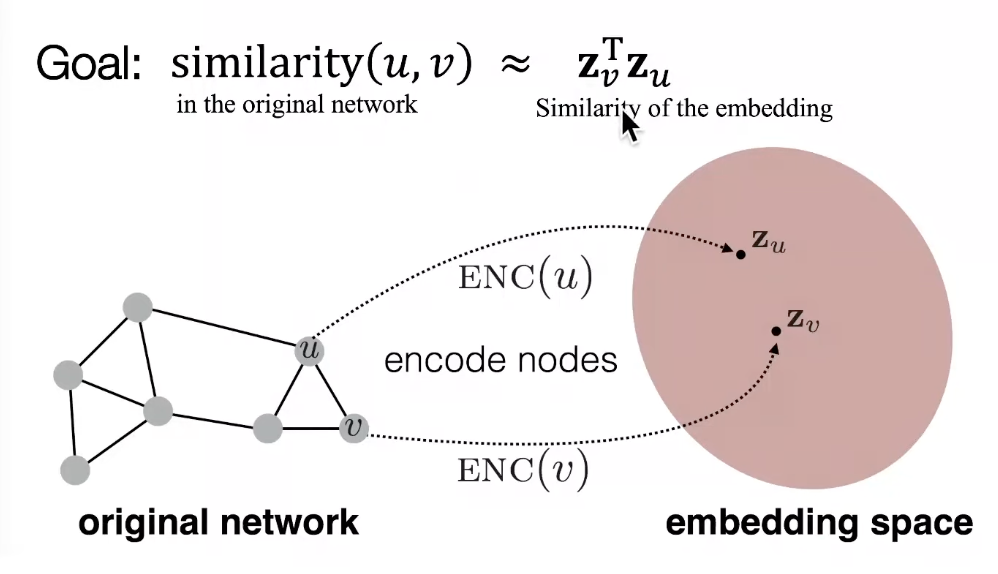
- Need to define : similairty functiona and objective function
Learning Node Embeddings
- Encoder maps from nodes to embeddings
- Define a node similarity function (a measure of similarity in the original network)
- Decoder DEC maps from embeddings to the similarity score
- Optimize the parameters of the encoder so that
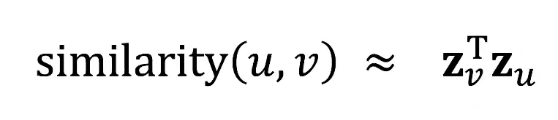
- Encoder: maps each node to a low-dimensional vector
- Similairty function: specifies how the relationsips in vector space map to the relationships in the original network
"Shallow Encoding" : Encoder is just an embedding-lookup (one column per node x dimension/size of embeddings)
Each node is assigned a unique embedding vector
Framework Summary
- Encoder + Decoder Framework
❍ Shallow encoder: embedding loopup
❍ Parameters to optimize: Z which contains node embeddings z_u for all nodes u in V
❍ We will cover deep encoders (GNNs) in Lecture 6
❍ Decoder: based on node similarity
❍ Objective: maximize the dot product of node pairs
How to Define Node Similarity?
- Key choice of methods is how they define node similarity
- Should two nodes have a similar embedding if they...
❍ are linked?
❍ share neighbors?
❍ have similary "structural roles"? - We will now learn node similairty definition that uses random walks, and how to optimize embeddings for such a similarity measure.
Note on Node Embeddings
- This is unsupervised/self-supervised way of learning node embeddings
❍ We are not utilizing node labels
❍ We are not utilizing node features
❍ The goal is to directly estimate a set of coordinates of a node so that some aspect of the network structure is preserved - These embeddings are task independent
❍ They are not trained for a specific task but can be used for any task.
Random Walk Approaches for Node Embeddings
Notation

Random Walk
- Given a graph and a starting point, we select a negihbor of it at random, and move to this neighbor; then we select a neighbor of this point at random, and move to it, etc. The (random) sequence of points visited this way is a random walk on the graph.
Random-Walk Embeddings

1. Estimate probabilty of visiting node v on a random walk starting from node u using some random walk strategy R
2. Optimze embeddings to encode these random walk statistics
Why Random Walks?
- Expressivity: Flexible stochastic definition of node similarity that incorporates both local and higher-order neighborhood information
- Idea : if random walk starting from node u visits v with high probability, u and v are similar (high-order multi-hop information)
- Efficiency: Do not need to consider all node pairs when traning; only need to consider pairs that co-occur on random walks
Unsupervised Feature Learning
- Intuition: Find embedding of nodes in d-dimensional space that preserves similarity
- Idea: Learn node embedding such that nearby nodes are close together in the network
- Given a node u, how do we define nearby nodes?
Feature Learning as Optimization

- Given node u, we want to learn feature representations that are predictive of the nodes in its random walk neighborhood N_R(u)
Random Walk Optimization
- Run short fixed-length random walks starting from each node u in the graph using some random walk strategy R
- For each node u collect N_R(u), the multiset of nodes visited on random walks starting from u
- Optimize embeddings according to: Given node u, predict its neighbors N_R(u)

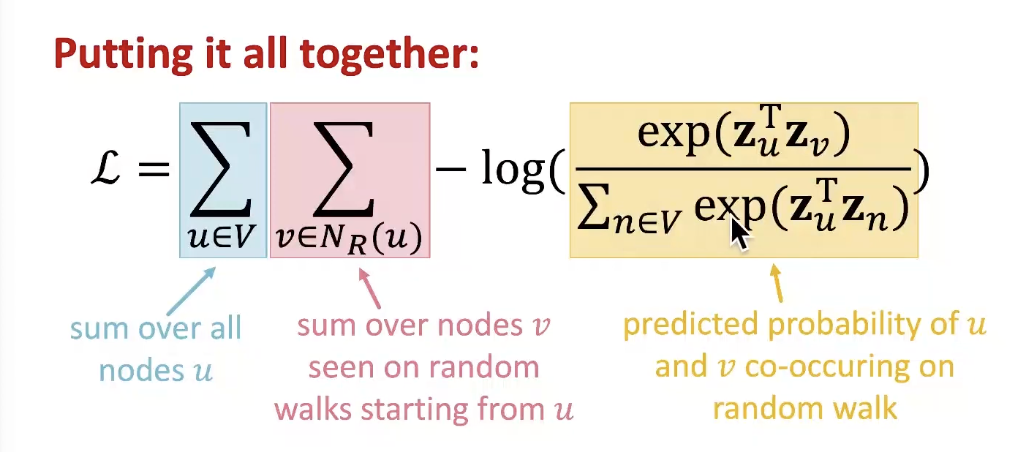
Optimizing random walk embeddings = Finding embeddings z_u that minimize L
- But doing this naively is too expensive!
Negative Sampling

Instead of normalizing w.r.t all nodes, just normalize against k random "negative samples" n_i
- Smaple k negative nodes each with prob. proportional to its degree
- Two considerations for k (#negative samples):
- Higher k gives more robust estimates
- Higher k corresponds to higher bias on negative events
Stochastic Gradient Descent
- After we obtained the objective function, how do we optimize (minimize) it?


Random Walks: Summary
- Run short fixed-length random walks starting from each node on the graph
- For each node u collect N_R(u), the multiset of nodes visited on random walks starting from u
- Optimize embeddings using Stochastic Gradient Descent (We can efficiently approximate this using negative sampling!)
How should we randomly walk?
- So far we have described how to optimize embeddings given a random walk strategy R
- What startegies should we use to run these random walks?
Overview of node2vec
- Goal: Embed nodes withs similar network neighborhoods close in the feature space
- We frame this goal as a maximum likelihood optimization problem, independent to the downstream prediction task
- Idea: use flexible, biased random walks that can trade off between local and global views of the network
BFS는 local한 값들은 알고 싶을 때 (Micro-view of neighourhood), DFS는 더 깊고 긴 관계를 알고 싶을 때 (Macro-view of neighbourhood)
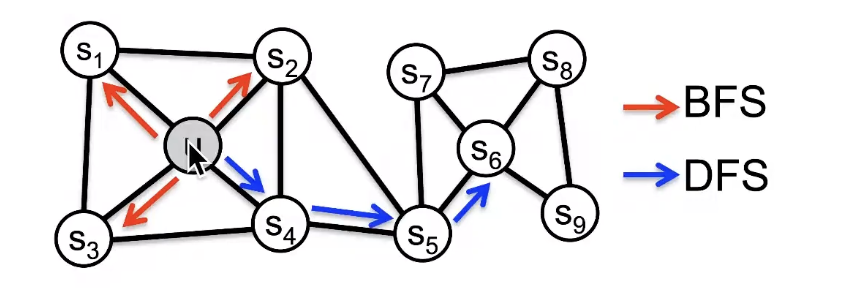
Interpolating BFS and DFS
Biased fixed-length random walk R that given a node u generates neighborhood N_R(u)
Two parameters
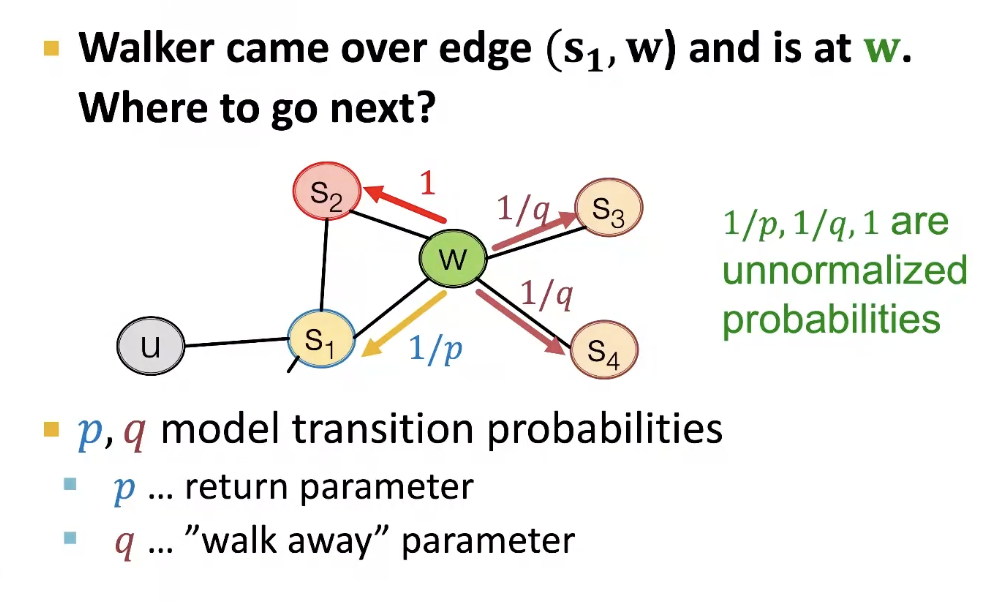
- Return parameter p : return back to the previous node
- In-out parameter q : moving outwards(DFS) vs. inwards(BFS), q is the "ratio" of BFS vs. DFS
Biased Random Walks
Biased 2nd order random walks explore network neighborhoods
- Rnd. walk just traversed edge (S-1, w) and is now at w
- Insight: Neighobrs of w can only be 여기에 머무르거나, 하나 더 level이 높아지거나, 낮아지거나
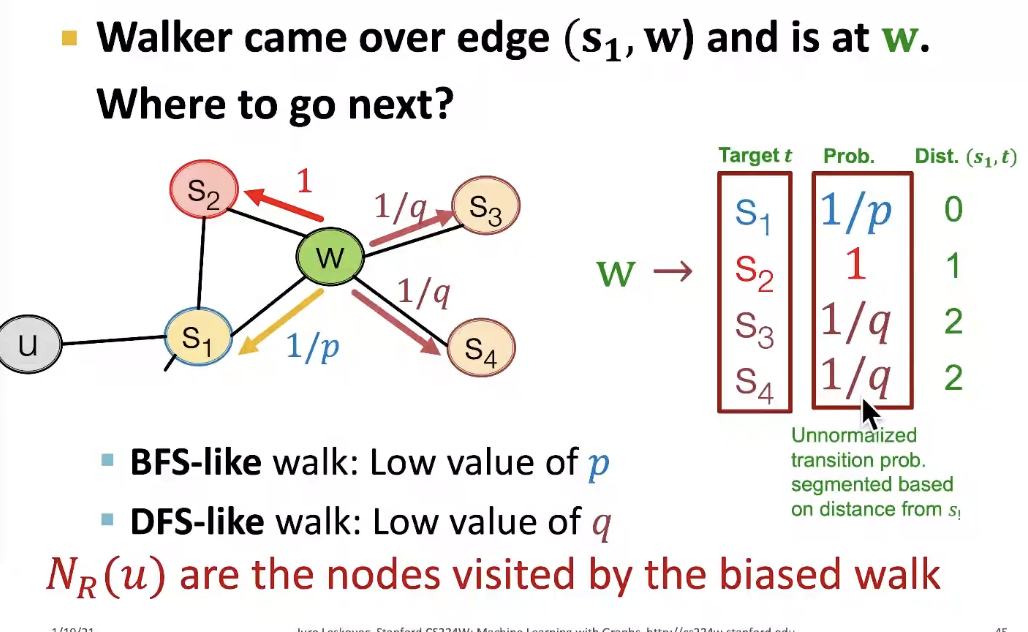
node2vec algorithm
- compute random walk probabilites
- simulate r random walks of length l starting from each node u
- optimize the node2vec objective using Stochastic Gradient Descent
- Linar-time complexity
- All 3 steps are individually parallelizable
Other random walk ideas
- different kinds of biased random walks : based on node attributes, based on learned weights
- Alternative optimization schemes : directly optimize based on 1-hop and 2-hop random walk probabilities
- Network preprocessing techniques : run random walks on modified versions of the original network
Embedding Entire Graphs
- Goal: Want to embed a subgraph or an entire graph G. Graph embedding: z_G
Approach 1
Simple Idea 1
- Run a standard graph embedding technique on the (sub)graph G
- Then just sum (or average) the node embeddings in the (sub)graph G
Approach 2
- Introduce a "virual node" to represent the (sub)graph and run a standard graph embedding technique
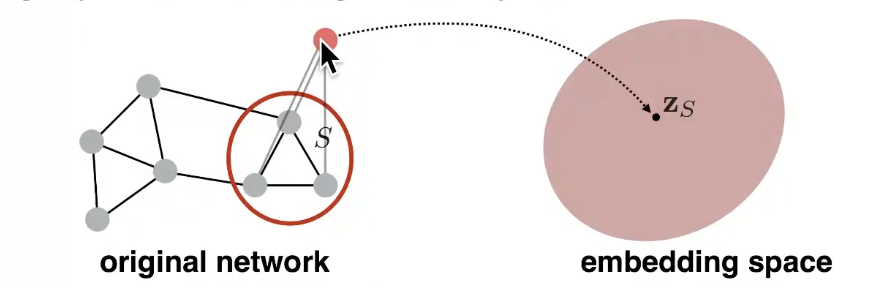
Approach 3
Anonymous Walk Embeddings
- States in anonymous walks correspond to the index of the first time we visited the node in a random walk (언제 sequence가 node를 제일 처음 방문했는지를 바탕으로 walk의 index 결정)
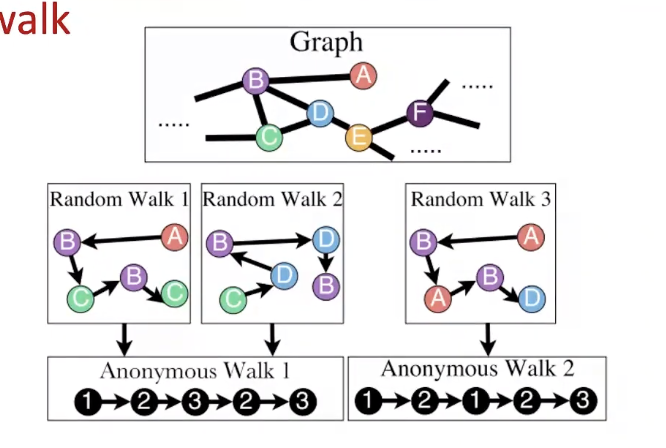
- Agnostic to the identity of the nodes visited (hence anonymous)
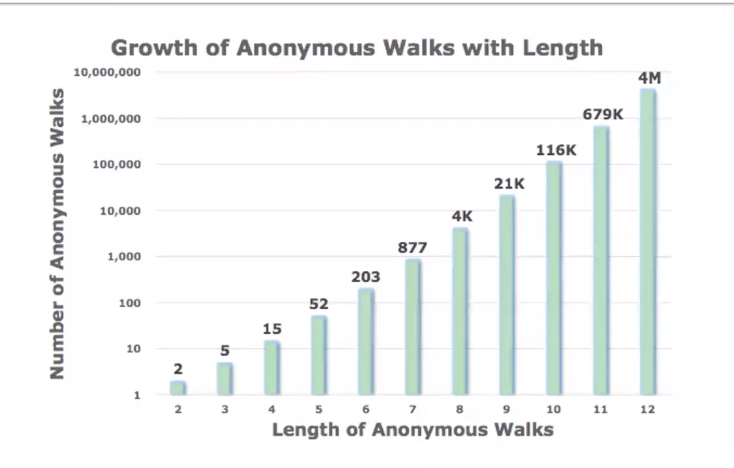
Number of Walks Grows
- Number of anonymous walks grow exponentially
Simple Use of Anonymous Walks
- Simulate anonymous walks w_i of l steps and record their counts
- Represent the graph as a probability distribution over these walks
Sampling Anonymous Walks
- Sampling anonymous walks: Generate independently a set of m random walks
- Represent the graph as a probability distribution over these walks
- How many random walks m do we need?

New idea: Learn Walk Embeddings
Rather than simply represent each walk by the fraction of times it occurs, we learn embedding z_i of anonymous walk w_i
- Learn a graph embedding Z_G together with all the anonymous walk embeddings z_i
- How to embed walk?


- We obtain the graph embedding Z_G(learnable parameter) after optimization
- Use Z_G to make predictions (e.g. graph classification)
Option 1. Inner product kernel
Option 2. Use a neural network that takes Z_G as input to classify
How to use embeddings

