Bias in Cross-Entropy-Based Training of Deep Survival Networks

Deep survival networks 에서는 크게 두 분류의 loss function 을 사용하여 타겟 네트워크를 optimize 한다. 첫번째로는 proportional hazard model 로부터 유도된 DeepSurv 에서 최초로 사용한 negative log likelihood 계열 loss 가 있고, 두번째는 event time 을 discretize 하여 fixed boundary 를 이용한 classification 계열 loss 가 있다. 본 논문에서는 survival analysis 에서 기존 사용되던 cross-entropy loss 에 특정 bias 가 끼여있음을 이론, 실험적으로 증명하고 이를 완화한 새로운 loss 를 제안하고 성능을 비교 분석한다.

Introduction

Discrete hazard function 과 discrete survival function 에 대해 먼저 설명하고 있다. 다음과 같이 정의된다.

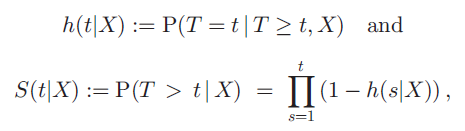
여기서 설명을 놓치면 앞으로도 계속 이해가 안갈테니 꼼꼼하게 짚고 넘어가는 것이 좋다. T 는 환자들의 event time 을 categorical value 로 만들어 놓은 discrete time variable 이다. 예를 들어 t_1 을 0 부터 100일 이런식으로 잡을 수 있는 것이다. X 는 환자의 time, event 정보 이외의 age, stage 등 환자의 survival 을 추정하기 위해 사용되는 variables 이다. h(t|X) 는 해당 환자가 (조건부) X 라는 variable 을 가지고 있고 t 라는 시간대까지 살아남았을 때, t 라는 시간대에 죽을 (event 가 일어날) 확률 이다. 이 때, 1-h(t|X) 는 그 여집합으로, 동일 조건에서 t 라는 시간대에 죽지 않을 확률로 해석할 수 있다. S(t|X) 는 t 라는 시간대에 죽지 않았을 확률 이다. 즉 이를 다시 표현하면, 첫번째 시간대부터 t-1 시간대, t 시간대에 죽지 않을 확률의 joint probability 로 볼 수 있다. 결국 deep survival network 를 통해 위 환자마다 계산된 output layer 의 real-valued output 로부터 hazard function h(t|X) 오른쪽 삼지창 (0,1] 를 추정하는 것이 목적이다.

그렇다면 기존 사용되던 cross-entropy loss 는 어떤 형태를 띄고 있을지가 궁금해진다. survival analysis 는 right-censored data 이기 때문에, censored data 와 uncensored data 가 다르게 계산되어 loss function 에 들어가야 할 것이다.

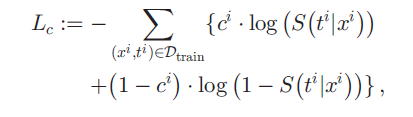
(xi, ti) 는 환자 한 명의 정보이다. ci 는 censored 되었는지 즉 event 가 일어났는지를 의미한다. censored data, event 가 일어나지 않은 patient 는 ci = 1 로 표기되기 때문에, ci 가 앞에 붙은 항은 event 가 일어나지 않은 patient 에 대해서만 계산되는 항이다. 반대로 (1-ci) 가 앞에 붙은 항은 event 가 일어난 patient 에 대해서만 계산되는 항이다. 위 식의 ci 가 붙은 항 S(ti|xi) 는, "event 가 일어나지 않은 patient 가, ti 에 안 죽어 있을 확률" 이다. 그리고 (1-ci) 가 앞에 붙은 항 (1-S(ti|xi)) 은 "event 가 일어난 patient 가, (언제 죽었는지는 모르지만) ti 에 죽어있을 확률" 이다. 논문의 저자는 이 (언제 죽었는지는 모르지만) 때문에 bias 가 낀다 설명한다. 그 환자는 t_i 시간대에 딱 죽은 환자인데, loss 에는 언제 죽었든 t_i 에 살아있기만 하면 계산이 되지 않도록 설계되어 있기 때문이다.

Theoretical Analysis of the Cross-Entropy loss

Comparison of the Cross-Entrop loss and the Negative Log-Likelihood loss

저자는 다른 논문의 discrete survival model 에서 사용된 log-likelihood function 을 벤치마킹하여 loss 를 설계한다.

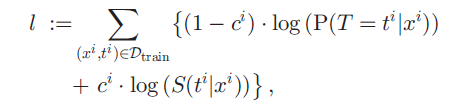
(1-ci) event 가 일어난 환자가 ti 라는 시간대에 딱 사망할 확률 + ci event 가 일어나지 않은 환자가 ti 라는 시간대에 생존해 있을 확률 이다. 이를 이리저리 잘 바꾸고 negative log likelihood 꼴로 만들어 다음과 같은 loss 로 변형한다.

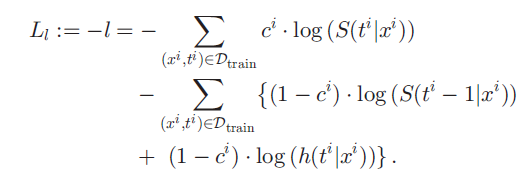
ci event 가 일어나지 않은 환자가 ti 시간대에 생존해 있을 확률 + (1-ci) event 가 일어난 환자가 ti-1 시간대까지 계속 생존해 있을 확률 + (1-ci) event 가 일어난 환자가 ti 시간대에 딱 사망할 확률 로 해석할 수 있다.

기존 사용되던 cross-entropy loss 와 새롭게 고안한 negative log-likelihood loss 의 차를 계산하면 다음과 같다.

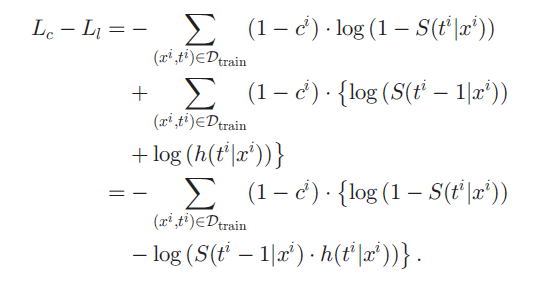
크게 봤을 때 두 loss 의 차이는 (1-ci), event 가 일어난 환자들에 의해 일어난다. 만약 모두 censored 되어 모든 환자의 ci=0 이라면 두 loss 는 같을 것이다. 좀 더 구체적으로 보면, (1-S(ti|xi) 가 S(ti-1|xi) * h(ti|xi) 에 가까워 질수록 두 loss 의 차이는 줄어든다. 이 두 식을 해석하기 편하게 정리하면 다음과 같다.

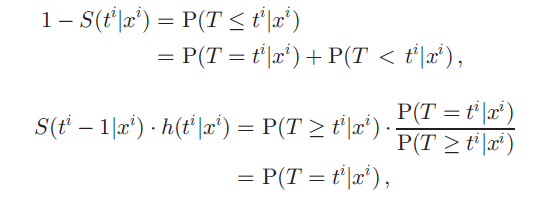
첫번째는 ti 에 이미 환자가 죽어있을 확률을, ti 에 죽을 확률과 ti 이전에 죽을 확률로 나눈 것이다. 그 아래의 hazard function 은 조건부를 분모로 보낸 것이다. 두 차이는 P(T < ti|xi) 로 정리되고, 이 식이 0으로 가면 두 loss 의 차이가 0 으로 간다. 결국 event 가 일어난 환자에 대해, 모든 ti 에 대해, P(T >= ti | xi) = 1 일수록 차이가 줄어든다는 뜻이고, 이를 다시 해석하면, "large event times for all instances" 를 뜻한다. 하지만 large event times 를 가진 환자는 (보통 오래 추적하기 어려우므로) 대게 censoring rate 가 높아 censoring rate 가 낮으면 어쩔 수 없이 발생하는 오차라고 설명한다.

Bias in Cross-Entropy-Based Hazard Estimates

cross-entropy loss 로부터 발생하는 bias를 설명하기 위해, constant hazard function h(t|X)=h for all t 를 잡고 simulation 한다. 또한 censoring rate 를 0 부터 1까지 다르게 하여, 어떻게 추정치가 달라지는지를 plot 한다.

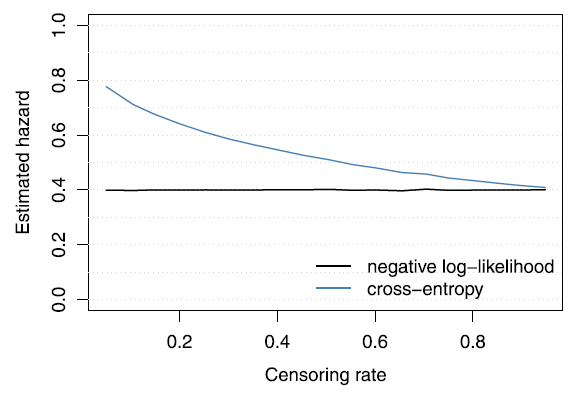
결과, 계산대로 censoring rate 가 낮을수록 (event 가 일어난 환자가 많을수록) cross-entropy 와 negative log-likelihood 사이 큰 차이가 존재했고, censoring rate 가 1 에 가까워 질수록 그 차이는 줄어들어 갔다. 또, cross-entropy loss 를 사용했을 때 hazard rate의 overestimation 과 survival function 의 underestimation 을 관찰하였다.

Empirical Evidence

이론적으로 difference 및 bias 가 존재함을 보이고, 실제 사용되는 deep survival network (DRSA network, DeepHit network) 에서 사용되는 cross entropy loss 를 고안한 negative log-likelihood loss 로 대체하여 실험을 진행하였다. c-index와 calibration 정도를 나타내는 GND test, survival function과 KM curve 의 비교를 통해 performance 를 비교하였다. 또한 다음과 같은 regularization term 앞에 alpha 를 곱해 두 loss 에 추가하여 성능을 비교하였다.

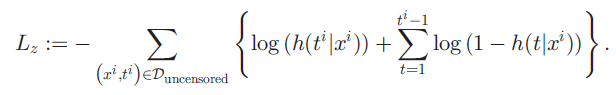
이 alpha 가 커질 수록, uncensored data 에 더 weight를 크게 한 loss 가 계산되어 network에 update 된다.

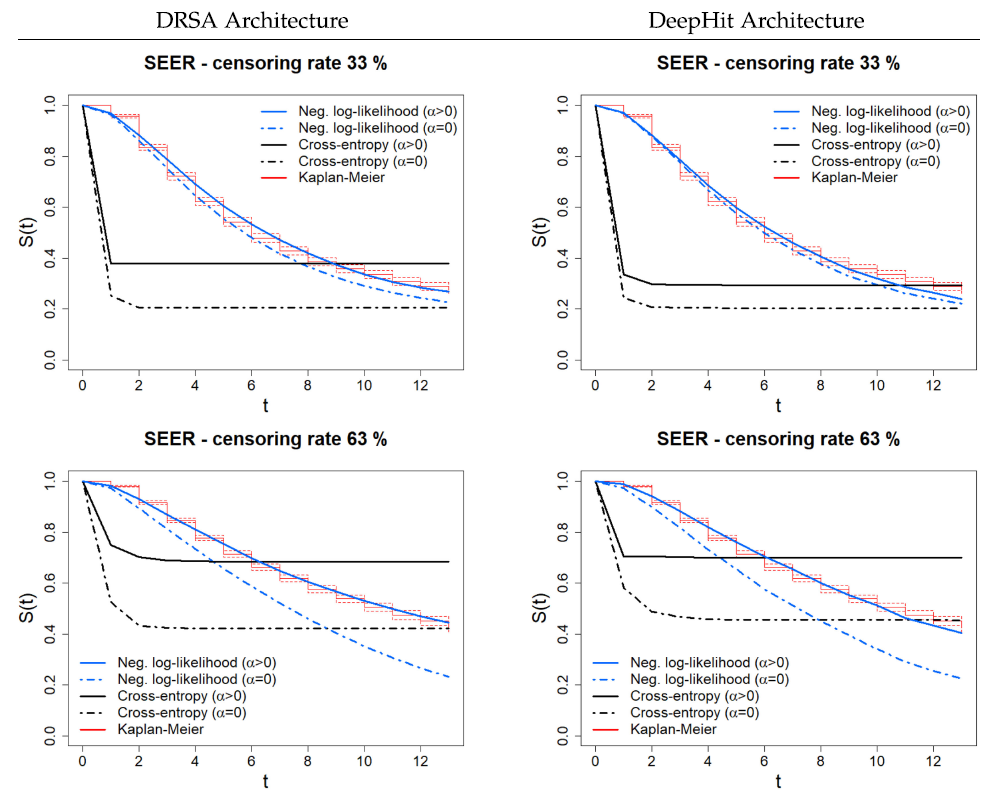
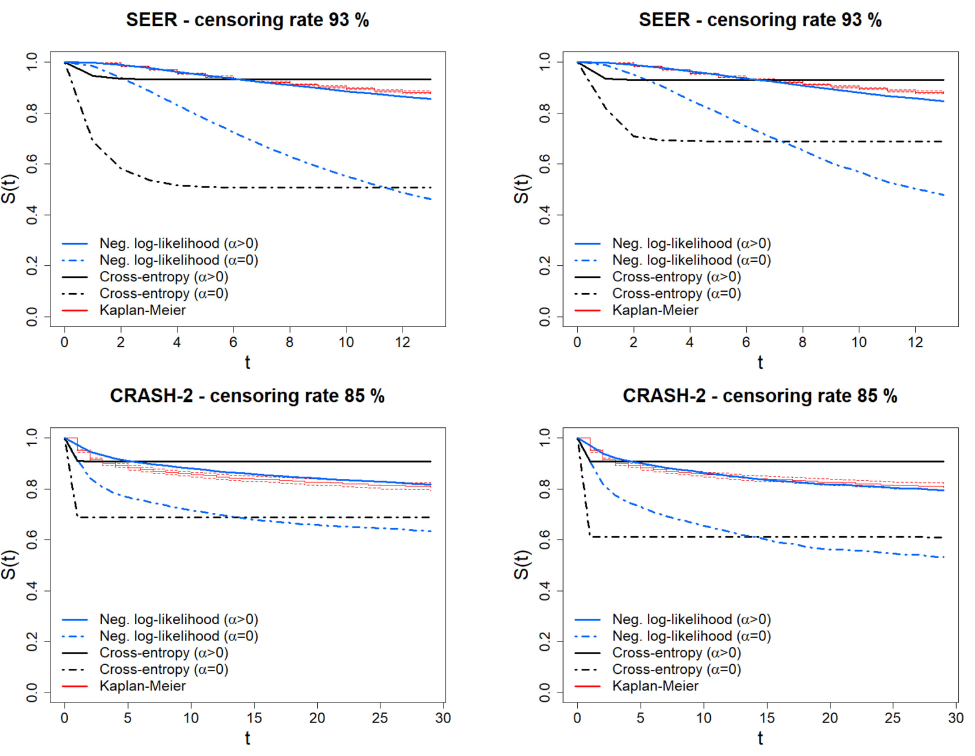
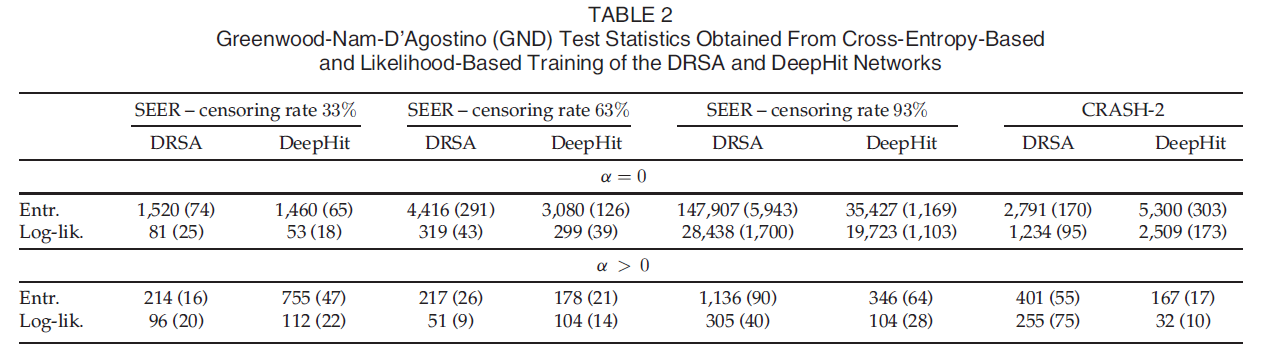
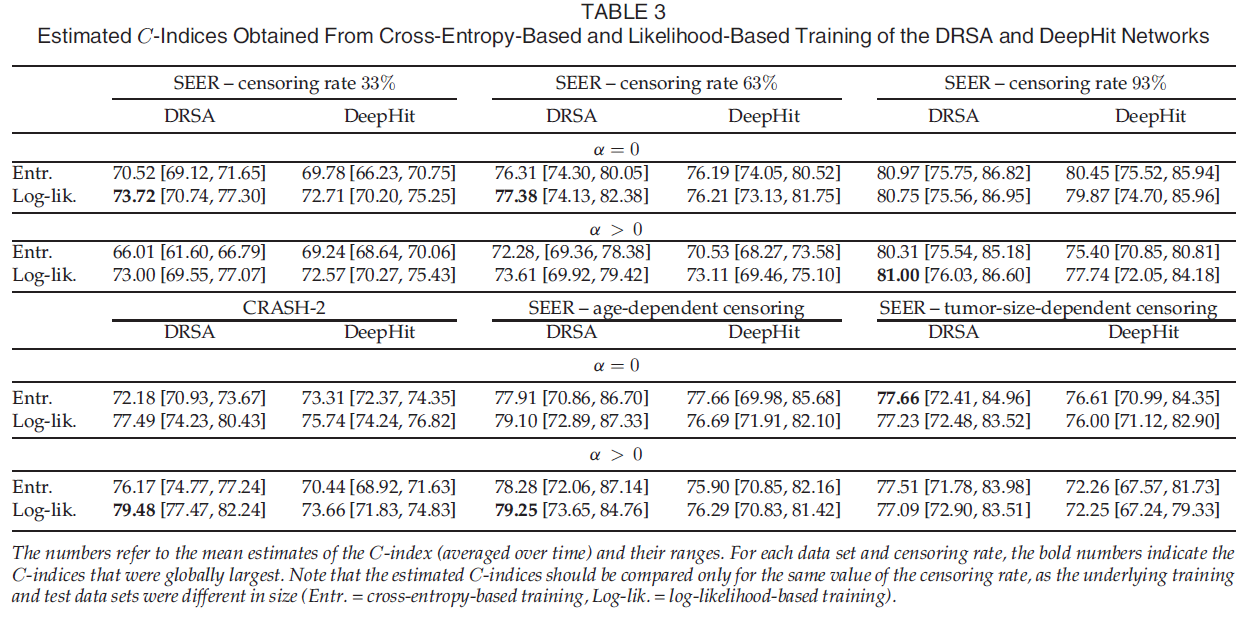
다음과 같은 결과를 얻었고, alpha 는 전반적으로 좋은 결과를 내었지만 특히 unbalance 된 데이터 일 때 좋은 결과를 얻었다. GND test 결과는 크면 클수록 덜 calibration 된, 즉 bias 가 껴있음을 나타내는데, 새롭게 고안된 loss 와 alpha 를 적용했을 때 calibration 이 훨씬 잘 됨을 보여준다. 또한 ranking performance 또한 전반적으로 개선되었다.

Conclusion

본 논문에서 진행한 theortical / empirical analysis 결과를 통해, cross-entropy-based training of deep survival network 는 large prediction error 과 함께 bias 를 초래함을 증명하였다. 이와 반대로 새롭게 고안한 loss 를 적용했을 때 better calibrated prediction rule 을 보였고, predicted survival probabilities 에서 smaller bias 와 함께 reduce prediction error 함을 보였다.

cf) 구현도 매우 간단했다..! --> ce_l ㄱㄱ