Emergence of Hidden Capabilities: Exploring Learning Dynamics in Concept Space

using generative model, this paper proposes concept space to evaluate a model's learning dynamics in this space. each abstract coordinate sytem indicates specific concepts including size, color, background color.

• introducing concept space
• concept signal dictates speed of learning
• sudden transition in concept learning

Concept Space: A Framework for Analyzing Concept Learning Dynamics

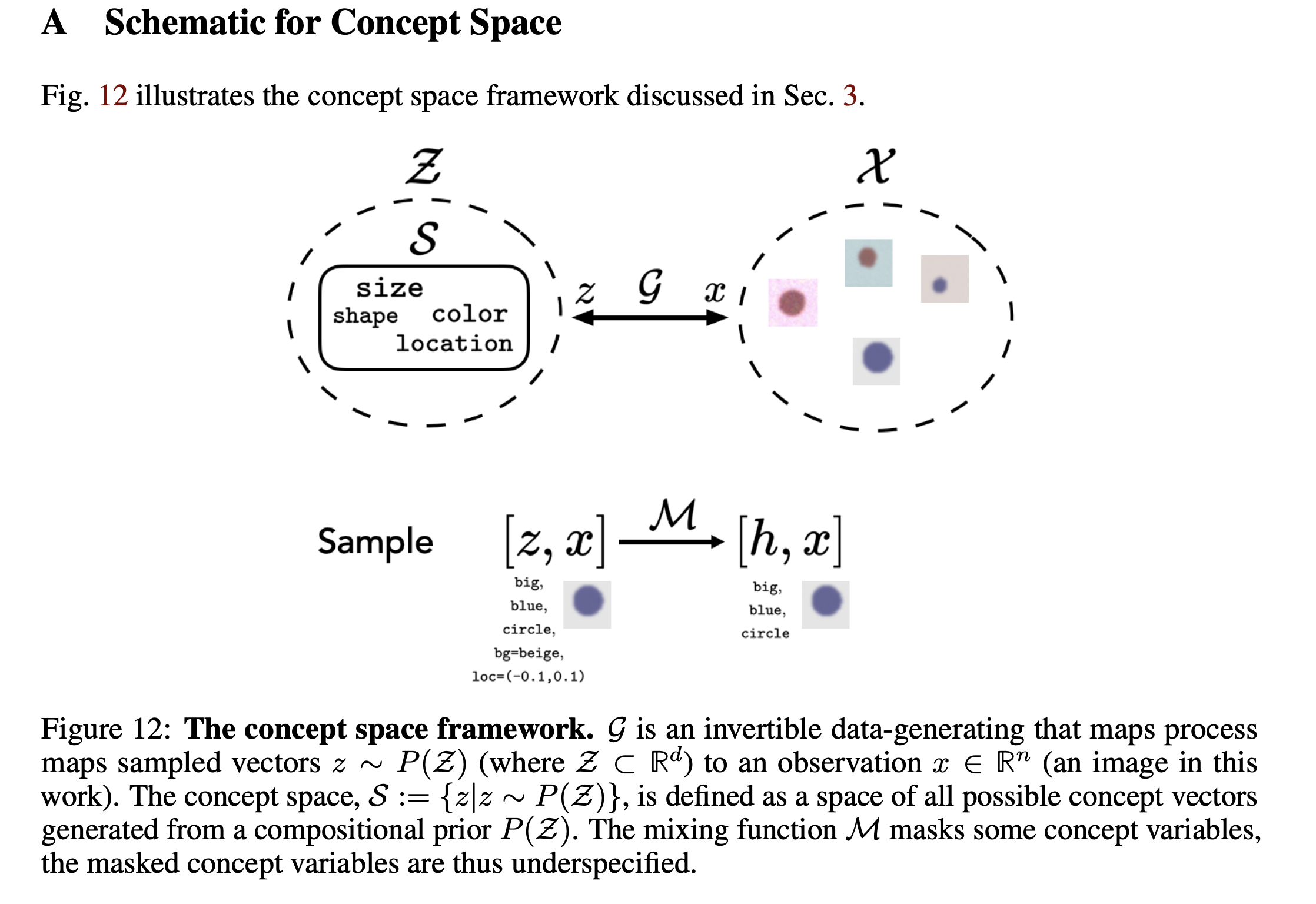
z is the full high-dimensional latent representation in the concept space, while h is the observed input derived from z with some components masked or reduced.

z represents the complete underlying structure for data generation, and h is a partial view provided as input for the model to learn. The model uses h to infer or align with the full representation z.

ex) z contains actual size, shape, background "representations"
ex) h contains low dimensional and (sometimes) masked representations like 01, 10, 11

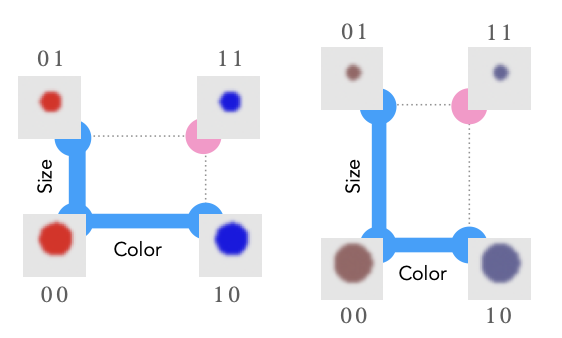
In this paper, they often mention the strength of "signal".
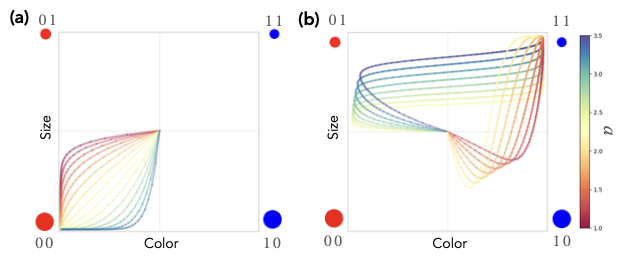
(left) color separation is stronger than size separation.
(right) size separation is stronger than color separation.

Experimental and Evaluation Setup

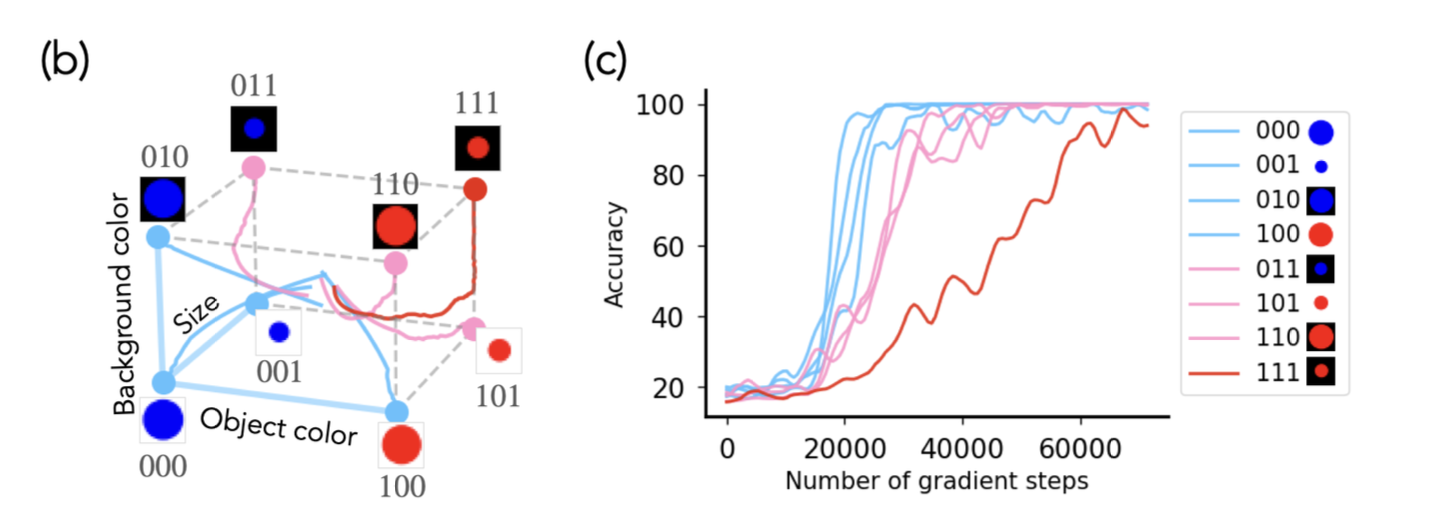
• experiments were conducted on 2D space using size and color variables and intentionally excluded one combination one case which could be trainied by combining concept.
• 00 (large red circles), 01 (large blue circles), and 10 (small red circles) (train) -> 11 (small and blud) OOD
• followed disentangled representation learning. (diffusion, U-Net)

Concept Signal Determines Learning Speed

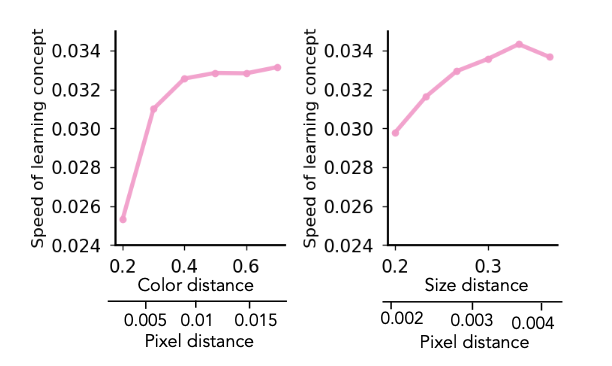
• RGB contrast on color, size difference --> controlled concept signal strength
• speed of learning definition: inverse of the number of gradient steps required to reach 80% accuracy for class 11 (OOD)
• concept signal determines the speed at which individual concept are learned

Concept Signal Governs Generalization Dynamics

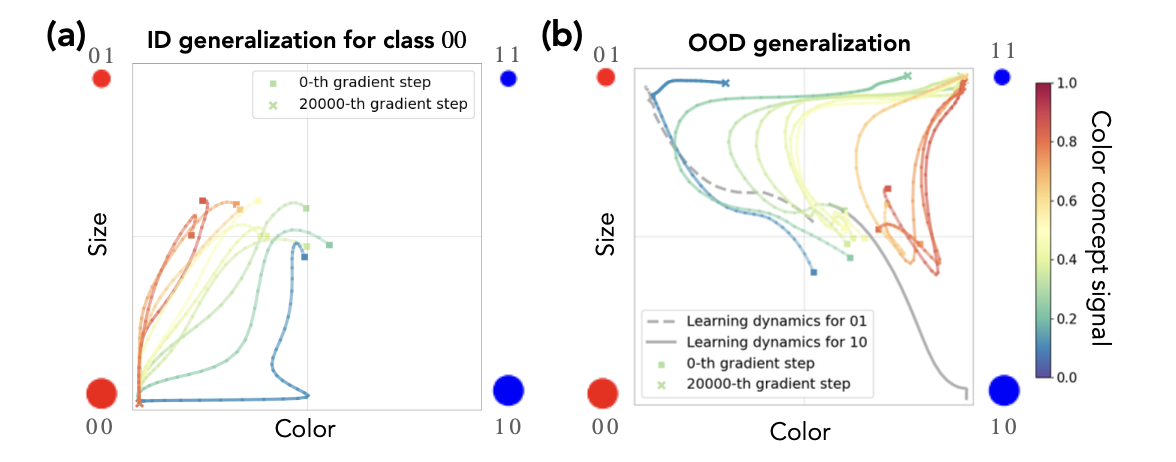
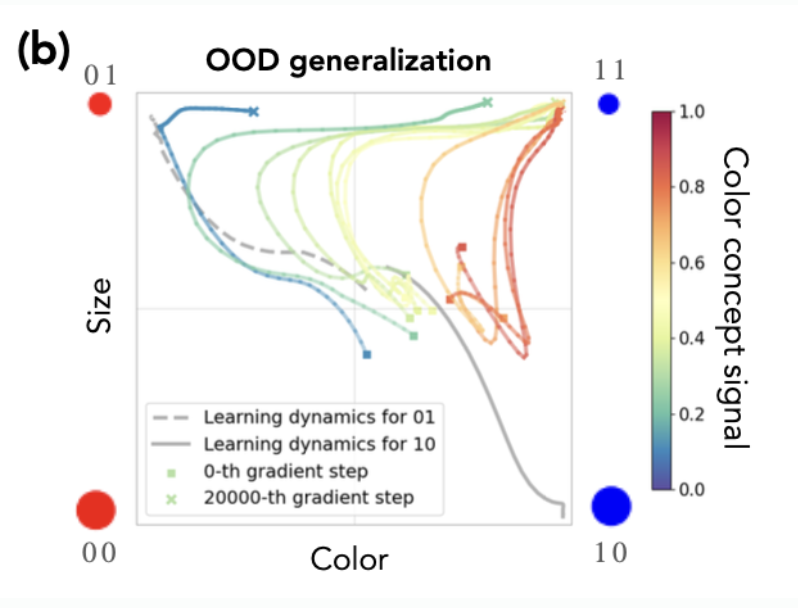
• color concept signal is relative strength of color compared with strength of size signal
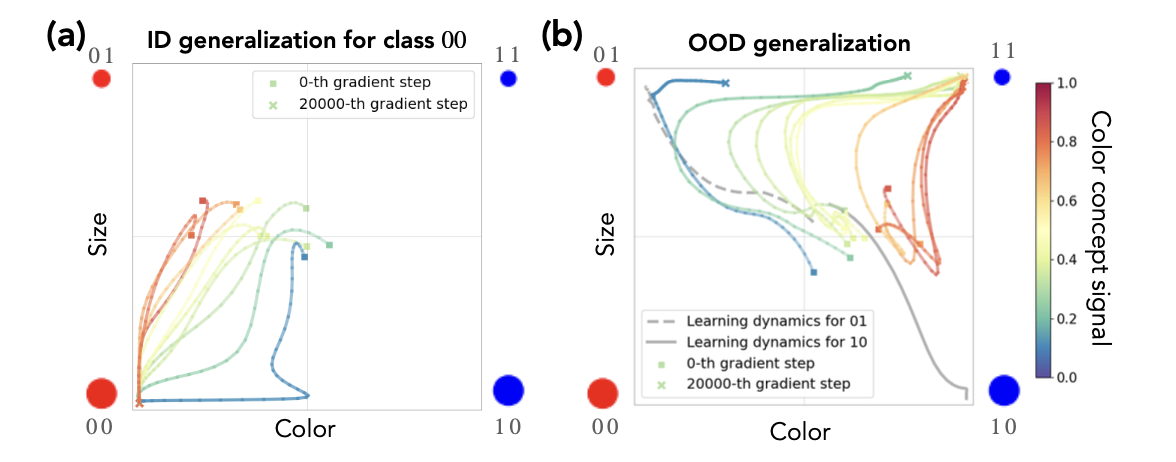
• when in distribution generalization for class 00, the trajectory converges to 00 regardless of their color concept signal.
• however, in OOD generalization, they first go toward in distribution concept like 01 or 10 depending on color concept signal and suddenly changes their trajectory towards 11.
• concept memoraization
• imbalance of concept signal strong --> strongly biased (look at blue trajectory on (b))
• states potential problem of early stopping.

Towards a Landscape Theory of Learning Dynamics

they tried to explain the phenomology of learning dynamics in concept space using analytical curves (dynamics equation below)

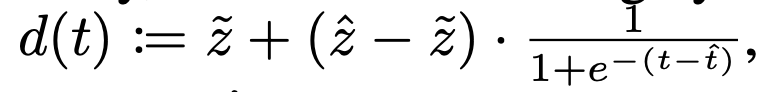
• where $\hat{z}$ is target point, $\tilde{z}$ is initial biased target. $\sigma$ is strength of signal. $\sigma_1$: color concept signal, $\sigma_2$: size concept signal
• ($\hat{z}_1$, $\hat{z}_2$) = (0, 1) indicates the representation of small size and red color. when $\sigma_2$ is larger than $\sigma_1$, in other words trajectory color is blue, they showed bias towards (0,1)
• this equation uses 1+exp(-t-t^) which is very similar to memory decay.

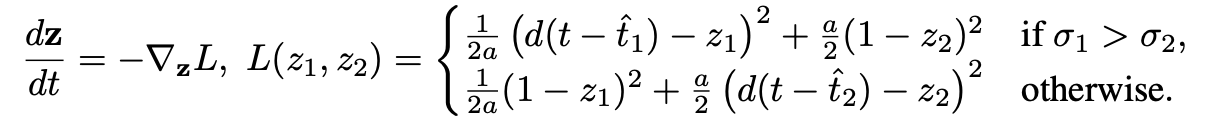
based on this framework, they derived above energy function. a is difference between $\sigma_1$ and $\sigma_2$ and $\hat{t}_1$ and $\hat{t}_2$ is the time when they learned concepts $z_1$ and $z_2$.

• this figure illustrates the simulated trajectories for classes 00 (a), and 11 (b) which is very similar to previous ID / OOD generalization figure.

• the network's learning dynamics can be decomposed into two stages :first biased toward ID sample and suddenly goes to OOD sample. --> existence of phase change underlying the decomposition and model acquires the capability to alter concepts

Sudden Transitions in Concept Learning Spaces

• at the point of departure (phase change), the model has already learned to manipulate concepts, causing a shift in its learning trajectory.
• however, in naive prompting, model fails to elicit these learned capabilities, making the model seem incomplete.
• to handle this insufficiency, they use new two prompting methods.

about linear latent intervention :
1. the model first identifies a vector representing a specific concept, such as "blue," by transforming the corresponding latent concept vector into the model's latent space.
2. Similarly, a vector for "large size" is created. The model then modifies the original concept vector by adjusting specific components to enhance or suppress certain attributes.
3. Increasing the weight of the blue concept strengthens its influence, while increasing the weight of the large-size concept reduces its effect.

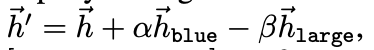
alpha, beta: hyperparameter.

analyzes the second-from-left curve (green), using checkpoints and two prompting methods to generate class 11 (blue, small).

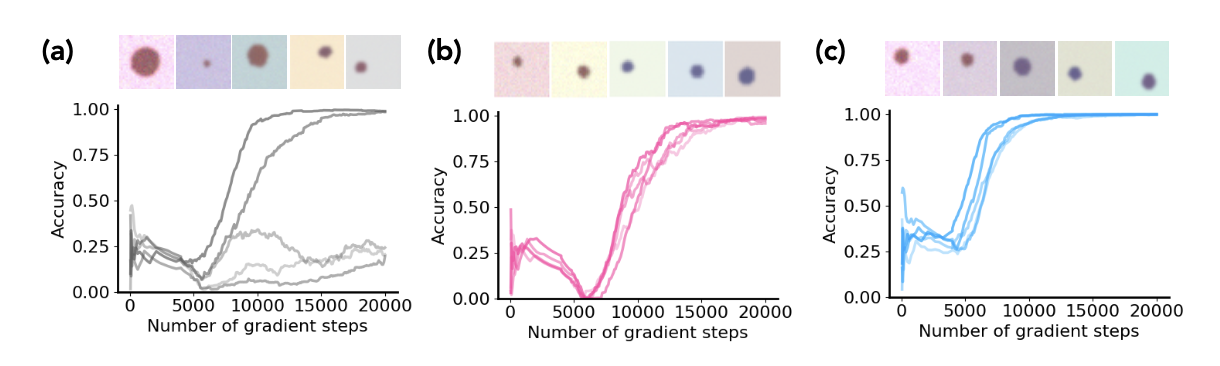
(a) naive input prompting: sometimes failed
(b, c) much faster. 6000 gradient step.

• this shows that the model can actually manipulate the concept and has capacity for OOD generalization.
• Also, in every prompting method, there were sudden turns where training trajectories suddenly changes. In this period, they "Activates" the ability of manipulating on this concept space. (??)

Effect of Underspecification on Learning Dynamics in Concept Space

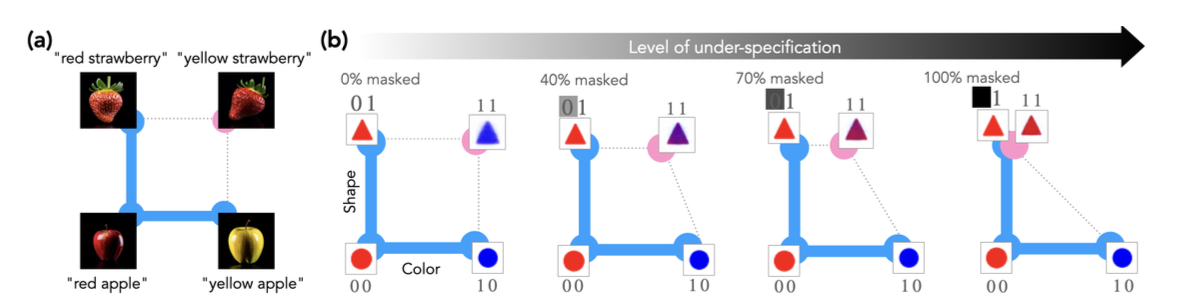
• in sota generative model, when yellow strawberry is given, the model actually generates red strawberry.
• similar to this, they randomly select training samples that have a specific combination of shape and color (like red triangle) and mask the token representing the color (red) and train the model on three concep classes (00, 01, 10).

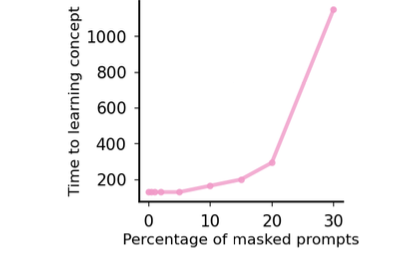
• the number of gradient steps required to reach accuracy 0.8 increases with percentage of masked prompts.

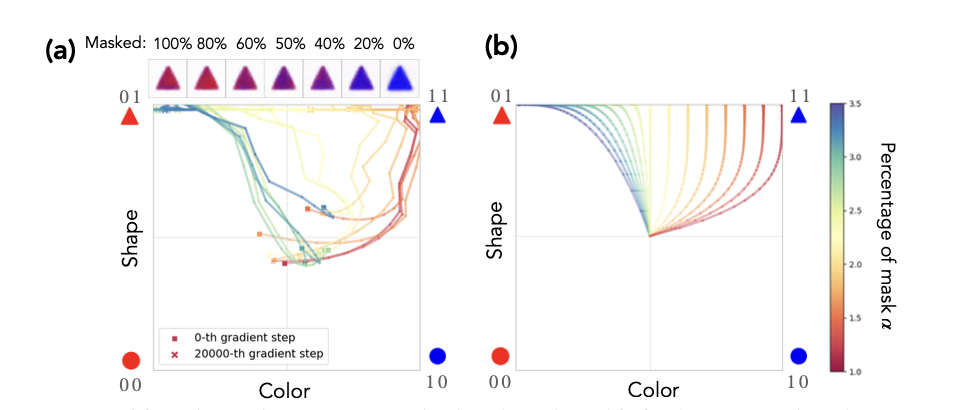
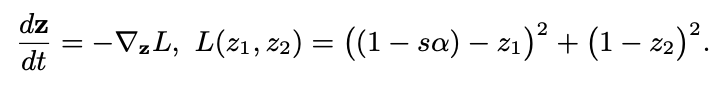
• underspecification delays and hinders OOD generalization
• toy model also exhibits similar plots

very interesting paper