Approximation and Optimization Theory for Linear Continuous-Time Recurrent Neural Networks

Intro

This is a summary of selected parts from the paper, focused on understanding the "curse of memory," rather than a review of the entire content.

this paper addresses whether continuous-time RNNs can approximate time-dependent functionals $H_t(x)$, which map input signals $x(t)$ to outputs $y(t)$. Unlike prior studies, this work emphasizes:

• The "absence" of underlying dynamical systems for $H_t$.
• The necessity of memory decay for approximation.

Problem Formulation

• Initially described in a discrete setting with equations (1) and (2), the discussion transitions into the continuous setting.
  
• The continuous RNN dynamics are expressed in equation (17), leading to the representation in equation (18).

Universal Approximation Theorem (Theorem 7)

• Using the Riesz-Markov-Kakutani theorem, the existence of $H_t$ is shown through its unique association with a measure $\mu_t$.

• The kernel representation $H_t(x) = \int_0^\infty x^\top_{t-s} \rho(s) \, ds$ (equation (23)) is central, where $\rho$ dictates smoothness and decay properties of input-output relationships --> convolution.

• equation (23) underscores kernel $\rho(t)$'s role in input-output convolution

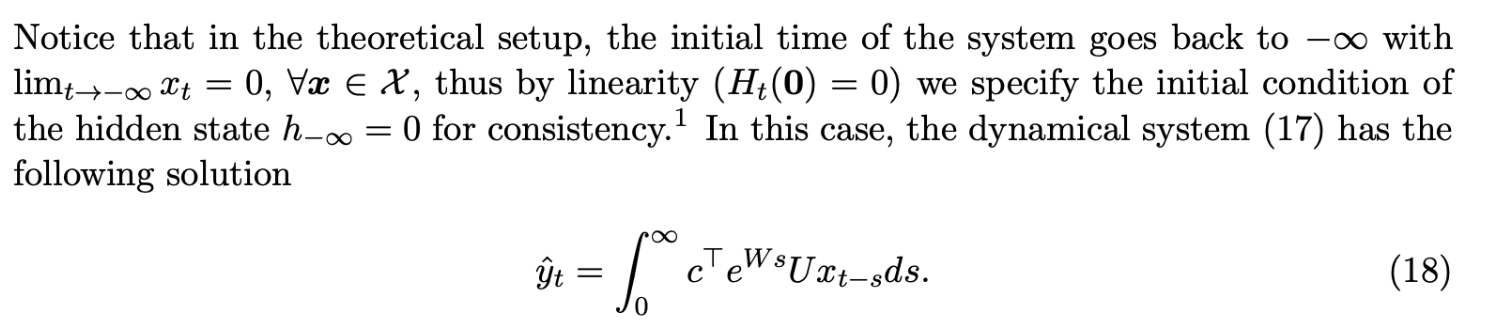
• The quality of approximation depends on how well $\rho(t)$ can be represented by exponential sums.

• The eigenvalues of $W$ with $\text{Re}(\lambda) < 0$ ensure system stability.

Approximation Rates (Theorem 10) and Inverse Approximation Theorem (Theorem 11)

• I couldn't understand the full proof process...
• (yet,) this provides bounds for approximating functionals under smoothness ($\alpha$) and decay ($\beta$) conditions, leading to approximations via width-$m$ RNNs with bounded error rates (equation (27)).
• In other words, although it may seem complex, the function is $\alpha$-smooth (continuous and differentiable), and its derivatives are controlled by a decaying rate of $\beta$ as in (25). When the decaying rate and the smoothness are related as shown in (26), width-$m$ RNN functionals $H_t$ can approximate the target under these bounds.

• demonstrates that without memory decay, approximation is infeasible. (amazing)
• again, i gave up understanding the proof haha..

Curse of Memory

• When $\rho(t)$ decays slowly (e.g., $\sim t^{-(1/\omega)}$), RNNs face exponential model size growth to maintain accuracy