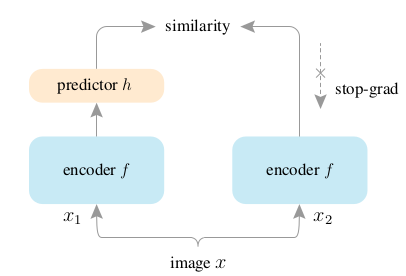
How Does SimSiam Avoid Collapse Without Negative Samples? A Unified Understanding with Self-supervised Contrastive Learning

Self-supervised learning 중 contrastive learning과 clustering 을 넘어, BYOL (bootstrap your own latent) 방식은 positive pair 과 momentum encoder 구조를 띄며 collapse 없이 학습이 이루어진다. 또한 SimSiam (simple Siamese networks) 은 negative sample pairs, large batches, 그리고 momentum encoders 없이 meaningful representations을 학습한다. 기존 SimSiam paper 에서 이 네트워크가 negative sample pairs 없이 collapse를 일으키지 않고 학습이 잘 이루어지는지에 대한 메커니즘을 설명했지만, 이번 논문에선 그 메커니즘을 여러 실험 디자인을 통해 반박하고, 새로운 메커니즘을 제시하여 이론적 / 실험적으로 증명한다.

Introduction

How does SimSiam avoid collapse without negative samples?
기존 연구에 따르면 SimSiam network 의 "stop gradient"와 "predictor h"가 중요한 역할을 했다 설명한다. 구체적으로 stop gradient 를 통해 alternative optimization 이 이루어지고, predictor 를 통해 expectation over augmentation 의 근사로 발생했던 gap 의 완화가 이루어지기 때문이라 설명한다.

저자는 위 두 메커니즘을 반박하고, representation vector 를 두 성분 (centor component 와 residual component) 으로 decompose 하고, 각각 dimensional collapse 에 어떤 역할을 수행하는지 관찰한다. 이 실험 디자인 속에서, "extra gradient component" 없는 basic Siamese architecture 에서는 collapse 가 일어남을 보이고, extra gradient component 의 center component 는 "de-cetering", residual component 는 "dimensional de-correlation" 을 통해 collapse 를 완화됨을 보인다.

또한 위 gradient decomposition 을 통해, 기존 contrastive learning 에서 자주 사용되는 InfoNCE loss 또한 de-centering 과 de-correlation effect 의 역할을 수행함을 보여 self-supervised learning 에서 통용되는 (unified) understanding 에 대한 insight 를 제공한다. 마지막으로 SimSiam 구조의 중요 역할을 수행하는 성분만을 이용해 collapse 를 막을 수 있음까지 보인다.

Revisiting SimSiam and its Explanatory Claims

l2-normalized vector and optimization goal
f(x) = z 라는 representation 이 있을 때, augmentation-invariant 한 representation 을 위해 두 positive sample 의 representation 간의 distance, mean squared error (MSE), 를 loss 삼아 minimize 한다. Scale ambiguity 를 방지하기 위해 vector들은 MSE 에 들어가기 전에 l2-normalized (Z = z/|z|) 된다. 그리고 사실 이는 cosine loss 와 동치다. 아래: Eq 1

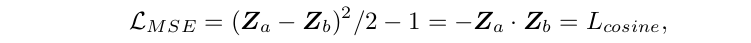
Collapse in SSL and solution of SimSiam
Eq 1 만으로 학습을 진행하면, 모든 output을 constant로 내놓아도 loss가 minimize 되므로 collapse 문제를 일으킨다. (저 Eq 1 만을 사용하는 구조를 "Naive Siamese" 라고 부를 것임.) SimSiam 구조에서는 "stop gradient" 와 "predictor h" 가 들어간 다음과 같은 loss 를 사용한다. 아래: Eq 2

Revisiting explanatory claims in SimSiam

AO: Alternating between the Optimization of two sub-problems
EOA: Expectation Over Augmentation

아래 식들은 기존 SimSiam 논문에서의 해석 (stop gradient as AO, predictor as EOA) 이다.

쉽게 설명해, stop gradient 를 통해 alternative optimization 이 가능해졌고, augmentation 을 epoch 마다 sampling 하는 것 만으로도 predictor 를 통해 augmentation distribution 을 학습하여 expectation over augmentation 과 sampling 사이의 gap 을 완화해주어 collapse 를 방지해 준다는 내용이다. 이 때, stop gradient 를 통한 효과에 대한 반박은 이전 연구에서 이루어졌다고 한다.

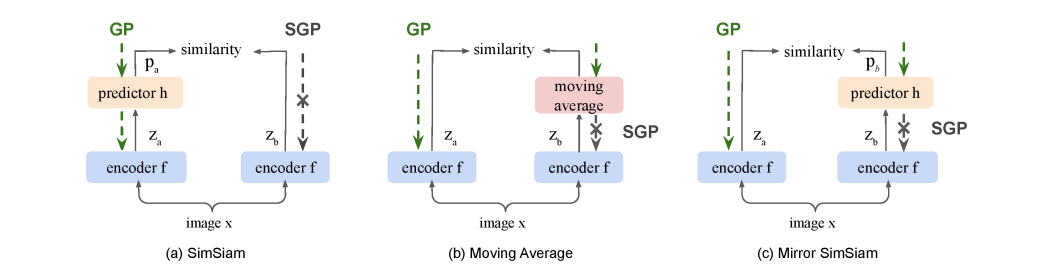
또한, 위 논리의 간극 (추측) 을 support 하기 위해 "predictor"로 EOA를 하지 않고, "$\eta_x$ 를 moving average 방식으로 update" 방식으로 EOA를 메꾼다 치고 실험을 진행한다. Predictor 가 없을 때 complete collapse 가 일어났고, moving average 가 없을 때 complete collapse 가 일어났기에 (naive siamese) 둘이 비슷한 방식 (EOA) 으로 collapse 를 완화한다 설명한다.

Does the predictor fill the gap to approximate EOA?

뭔가 이상한데? by reverse of GP and SGP
(c) 의 상황은 개념적으로 봤을 때 (a), (b) 와 유사하지만 SGP 가 적용되는 구간이 달라졌다. 이를 "Mirror SimSiam" 이라 부름. gradient path (GP) 와 stop gradient path (SGP) 를 바꿔서 배치했을 때 problematic 하다 생각한다. (이해 안감) 원문을 그대로 가져오면, It is worth mentioning that the Mirror SimSiam in Fig. 1 (c) is what stop gradient in the original SimSiam avoids. Therefore, it is problematic to perceive h as EOA. 라고 한다...

Explicit EOA does not prevent collapse
심샴 논문에선 다음과 같이 표현한다. In practice, it would be unrealistic to actually compute the expectation over augmentation. But it may be possible for a neural network (e.g., the preditor h) to learn to predict the expectation, while the sampling of T is implicitly distributed across multiple epochs. 저자는 multiple epoch에 거쳐 augmentation을 sampling하는게 beneficial 하면, 아예 배치 하나에서 augmentation 을 explicit하게 여러 번 sampling 해버리면 더 이득일 것이라 하고 predictor 없이 실험을 수행한다.

하지만 이는 collapse 를 막지 못했고, 오히려 augmentation은 적게 사용했지만 moving average 를 사용한 실험에선 collapse 가 일어나지 않았다. EOA 가 collapse 키퍼로써의 기능을 수행하지 못함을 증명한다.

Asymmetric interpretation of predictor with stop gradient in SimSiam

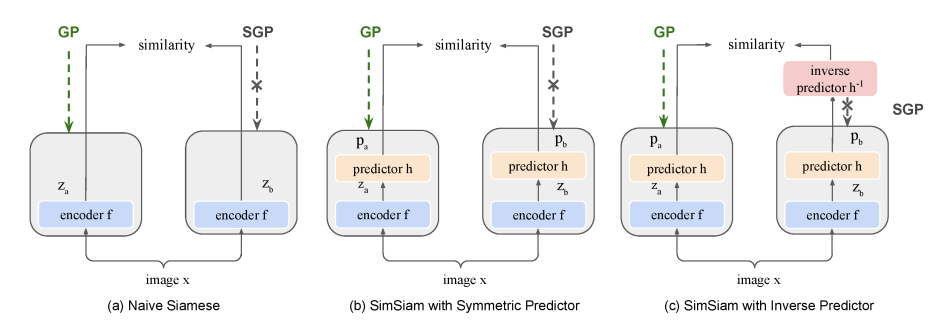
각 figure 아래의 주석으로 잘.. 따라가 봅시다.

Symmetric Predictor does not prevent collapse

위 table 결과를 보면, Naive Siamese, Symmetric Predictor 에서 predictor 가 있던 없던 symmetric architecture 를 가지면 collapse가 일어남을 확인할 수 있다.

Predictor with stop gradient is asymmetric
SimSiam의 avoid collapse 는 비대칭 구조에 있다라고 할 수 있어졌다. 구체적으로, Mirror SimSiam에서도 collapse 가 일어나는 것을 보면, predictor 가 없는 쪽이 SGP 여야 collapse 를 막을 수 있다. 이를 다시 표현하면, SimSiam avoids collapse by excluding Mirror SimSiam which has a loss as $L = -(P_a Z_b + P_bZ_a)$, where stop gradient is put on input of h, $p_a = h(sg[z_a])$.

Predictor vs. inverse predictor
흥미로운 실험을 다시 하나 한다. h 를 z에서 p 로 mapping 하는 함수로 인지하고, SimSiam with Symmetric Predictor 실험 디자인의 SGP에 inverse predictor h-1를 넣어주는 것이다. 이 때 h-1을 optimization target으로 잡아줌으로써 collapse 가 발생하지 않았다. (나중에 이게 왜 그러냐면,, $h(Z_a)$랑 $Z_b$ 를 비슷하게 만들어 줌으로써 Z 자체의 correlation을 줄여줘서 collapse 막는건데, 저 $Z_b$에도 h 씌워지면 그 효과가 안 나타나서 그렇습니다.)

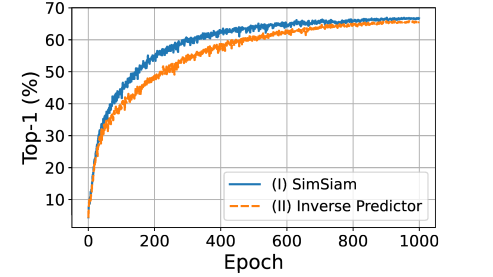
여기서, trainable h를 통해 collapse 가 막아지고, 성능이 어느정도 보장된다는 것을 확인함으로써, h 자체가 EOA 로써의 기능이 아님을 설명한다.

Vector Decomposition For Understanding Collapse

Vector Decomposition
Z 라는 representation vector를 $Z = o+r$로 분해하고, 각각을 center vector, residual vector 라고 부른다. 특히 o 는 whole representation space Z 의 average 로 설명된다. (o_z는 시그마 Z_m, M은 batch 사이즈) 그 vector를 제외한 부분을 r 이라 한다.

Collapse From the vector perspective

모든 solution이 collapse해서 $o_z$로 떨어지는 것은 아니지만, 일단 cause of collapse 를 분석하는 것이기에, o 를 consequence of the collapse 라 생각하고 분석을 진행한다.

Competition between o and r
$Z = o+r$ 에서 o와 r의 비율을 각각 $m_o$, $m_r$ 이라 정의한다. 이 때 저자는 cause of collapse 는 o와 r의 competition 중 o가 dominant 해버려서 발생한다고 해석한다. 아까 Naive Siamese 에서 사용된 Eq 1 에서 $Z_a$에 대한 negative gradient 는 다음과 같다. (아래껀 Eq 3)

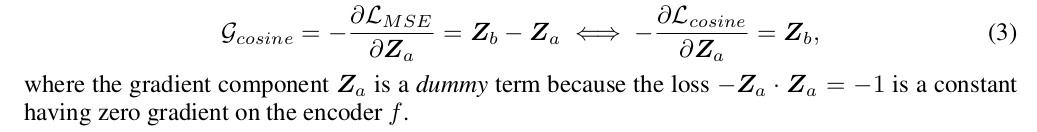
($Z_a$ 가 dummy 라 하는 부분이 잘 이해가 가지 않았음.) 저 gradient 에서 $Z_a$ 부분을 봤을 때, $Z_a = o_z + r_a$ 에서 $o_z$ 부분이 (gradient component) collapse 쪽으로 boost 할 것이다. 라는 Conjecture 1 을 잡는다. 이를 증명하기 위해서, dummy gradient term $Z_a$ (?) 로부터, $-Z_a * sg(o_z)$와 $-Z_a * sg(Z_a-o_z)$ 라는 loss 를 디자인 한다.

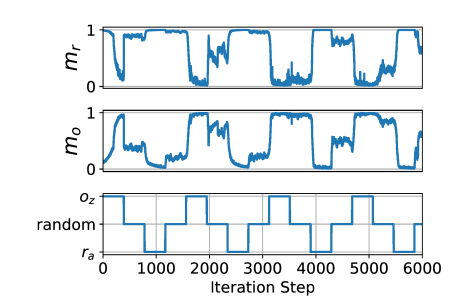
맨 아래 그래프처럼 loss 를 줘봤더니, gradient component $o_z$ 는 $m_o$를 increase 하는 effect 가 있는 것을 확인했다.

Extra Gradient Component for Alleviating Collapse

Revisit collapse in a "symmetric" architecture
이전 결과를 리마인드 해보면, predictor h 가 있던 없던, symmetric 구조는 모두 collapse 가 일어났다. 그 중 Naive Siamese 구조의 gradient를 뜯어보면 $Z_b - Z_a = (o_z + r_b) - (o_z + r_a) = r_b - r_a$ 이고, 이 때 $r_b$가 $r_a$ 처럼 positive sample 로부터 나왔기에 $m_r$을 increase 하는 방향으로 update 하겠지만, $r_a$ 자신의 영향 보단 약할 것이기 때문에 오히려 $m_r$을 decrease 하는 방향으로 update가 이루어져 collapse 한다고 설명한다.

Basic gradient and Extra gradient components

쉽게 말해, symmetric한 구조에서의 gradient 를 basic gradient 라 부르고, asymmetric 한 구조에서의 gradient 에서 basic gradient 를 제외한 것을 Extra Gradient $G_e$ 라고 부르자는 것이다. 예를 들어, SimSiam 의 negative gradient on $P_a$ (즉 $Z_b$) 를 $G_e$ $(Z_b-P_b)$ 와 $P_b$ 로 나눌 수 있는 것이다. ($P_a$ 의 basic gradient 는 $P_b$ 이기 때문!)

A Toy Example Experiment with Negative Sample

나이브 샴이 실패하는 원인으로, repulsive part 가 없음을 꼽는다. 그래서! contrastive loss 에서 어떤 repulsive component 가 collapse 를 방지하는지 알아보기 위해, triplet loss 로 실험을 진행한다.

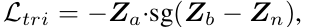
이 때, 저걸 $Z_a$에 대해 미분하면 $Z_b - Z_n$ 이고 Z_b 는 basic gradient component 니까 $-Z_n$ (negative sample 의 representation) 이 앞서 언급했던 $G_e$ 가 된다. 이를 o 와 r 로 나누어서 실험을 진행한다. 처음 가정은 위 실험 토대로 r component 가 avoid collapse 에 중요할 것 같다고 생각했는데, 현실은 아니었다.

오히려 removing r 을 했을 때 collapse 가 일어나지 않았고, removing o 를 했을 때 collapse 가 일어났다. Conjecture 1 과 견주어 봤을 때, 이 실험 결과를 $o_e = -o_z$ 라 해석하여, $o_e$ 가 오히려 센터로부터 벗어나게 해주는 de-centering role 을 수행할 것이라 설명한다. (이후 분석 나옴.) r은 그냥 noise 로 bahve 한다 생각.

Decomposed Gradient Analysis in SimSiam

이제 naive simsiam 이 아니라 SimSiam으로 돌아와서, eq 2 를 미분하면 다음과 같은 식이 나온다. Eq 4

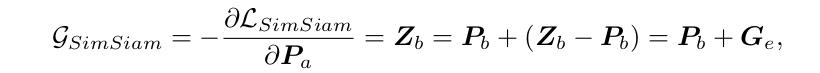
위와 같이, basic gradient 인 $P_b$를 우겨넣어서 $G_e$ 와 분리시킨다. 다시 이 extra gradient 를 center component 와 residual component 로 나누어서 실험을 진행한다.

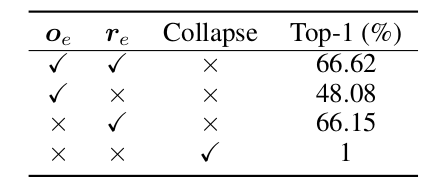
위 triplet loss 때와는 또 달리, 두 component 중 하나만 존재해도 collapse 를 막아내었다. 우선 $o_e$ 가 어떻게 막아냈는지를 분석한다.

How $o_e$ alleviates collapse in SimSiam
저 셋업에서 $G_e = Z_b - P_b$ 였다. 저 식을 잘 정리해보면, center gradient component 는 $o_e = o_z - o_p$ 이다. 이 때, conjecture 1 과 함께, 분석 대상은 $P_a$이기 때문에 만약 저 $o_e$ 가 contains negative $o_p$ 를 가지고 있다면, 설명이 된다.

cosine similarity 를 통해, $o_e$가 negative op 성분을 가지고 있음을 확인했다. 그렇기에 With Conjecture 1, this negative component explains why SimSiams avoids collapse from the perspective of de-centering.

마찬가지로, Mirror SimSiam 에 대해 동일한 framework 로 실험을 수행했을 때, 오히려 $o_e$가 positive $o_p$ 성분을 가지고 있었다. 이를 토대로 Mirror SimSiam 에서는 predictor h 가 둘 다 들어가는 것이 strengthen the collapse 함을 보였다.

Beyond de-centering for avoiding collapse
그렇다면,, 아까 triplet loss 에서의 $r_e$ 성분은 collapse 방지에 도움이 안됐는데, 왜 이번엔 $r_e$ 가 도움이 되었을까? 이를 이제 dimensional de-correlation 으로 설명한다.

Dimensional De-Correlation Helps Prevent Collapse

Conjecture 2 : Dimensional de-correlation increases $m_r$ for preventing collapse.
실험 디자인은 다음과 같다.
1) loss Eq 2 로 SimSiam 을 평범하게 train
2) 몇몇 epoch 에서 의도적으로 $m_r$ 성분을 close to zero 해서 train
3) correlation regularization term 을 이용한 loss 로 train

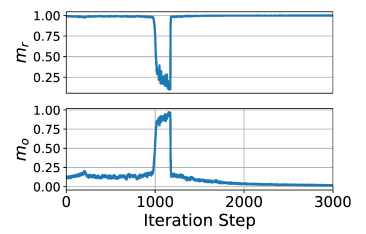
요기 보면, 처음에 2) 때문에 떨어졌다가, de-correlation regularization term 넣었을 때 $m_r$ 이 빠르게 상승하는 것을 확인함. (캬)

Dimensional de-correlation in SimSiam
predictor h 가 only has a single FC layer (??? to exclude the influence of $o_e$) 라고 가정해보자.
이 때, 기존 연구 결과에 따르면, h weight 의 eigenspace 와 encoder output 의 correlation matrix 가 align 한다고 했었으니, FC layer 의 weight 가 encoder output의 different dimension 간의 correlation 을 잘 학습할 것이라 예측하였다. 본질적으로, h는 본래 h(z_a) 와 I(z_b) 간의 cosine similarity 를 줄이는 방향으로 학습이 이루어지기 때문에, Z 자체의 de-correlation을 야기한다고 설명한다.

표에서 보았듯 $r_e$ 가 collapse 를 혼자서도 막았다는 결과와 추후 진행된 실험에서 r_e removal 파트에서만 covariance 가 높고, accuracy 가 낮게 나온 결과가 위 설명을 뒷받침한다.

Towards a Unified Understanding of Recent Progress in Self-Supervised Learning

SimSiam 이외에도 contrastive learning 과 같은 self-supervised learning 방식도, 동일한 framework 를 적용해 설명하려 한다.

Decentering and de-correlation in InfoNCE

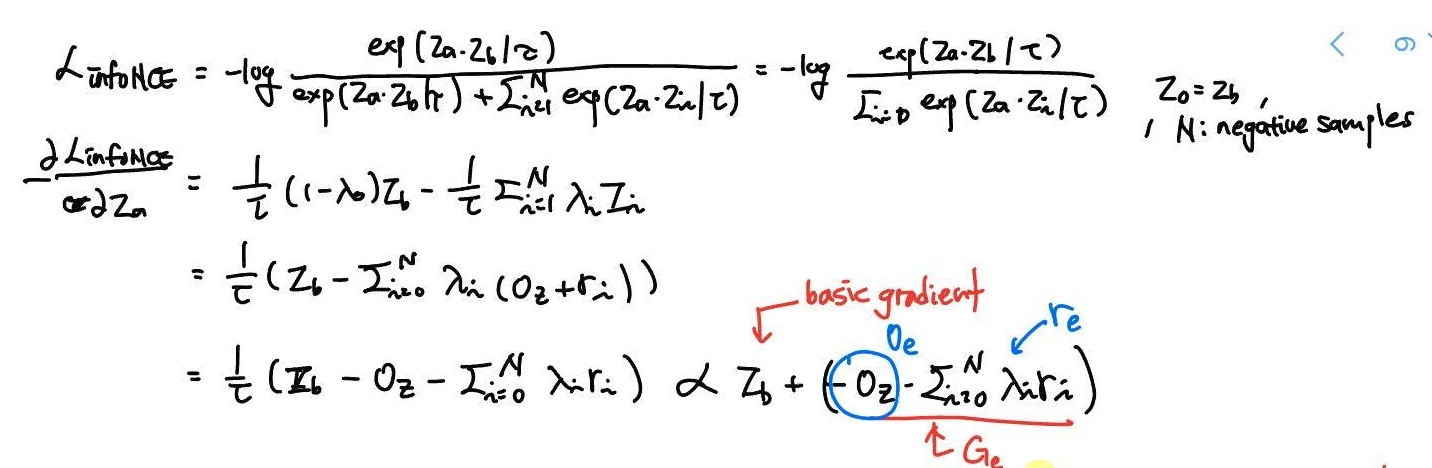
InfoNCE loss 를 $Z_a$에 대해 미분한 negative gradient 를 계산하면, 결국 basic gradient 와 extra gradient 성분으로 나눌 수 있다. (여기부터 집중해야 됨.) extra gradient의 residual component 에 붙어있는 weight 는 $Z_a$와 $Z_i$가 가까울 때 (correlation이 높을 때) 커진다. 그러므로, weight ($\lambda$) 가 작아지는, decorrelation 이 되는 방향으로 학습된다 라고 설명할 수 있는 것이다.

또한, de-correlation effect in InfoNCE 는 biased weights ($\lambda$) 로부터 나온다 를 보기 위해, temperature 에 따른 lambda 변화에 따른 각 성분과 "correlation regularization loss" 와의 cosine similarity 봤고, 특정 temperature 에서 similarity 높아진 것을 통해 가설을 보조 하였다.

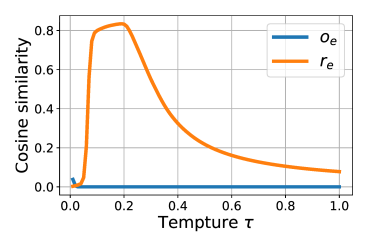
temperature 에 따라서 entropy 가 증가하는 것, temperature 에 따라서 accuracy 변화가 생기는 것, temperature 에 따라서 covariance 변화가 생기는 것을 통해 위 가설을 다시 corroborate 했다.

Towards Simplifying the Predictor in SimSiam

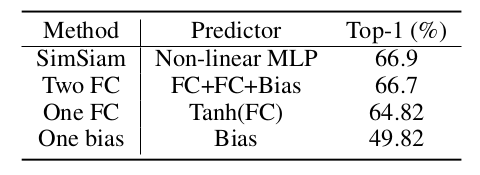
SimSiam network 에서 핵심 component 만으로 simplify 하여 성능을 측정한다.

• to achieve dimensional de-correlation
  : a single FC layer might be sufficient because a single FC layer can realize the interaction among various dimensions.
• to achieve de-centering
  : a single bias layer might be sufficient because a bias vector can represent the center vector

Conclusion

• 기존 SimSiam 논문에서 설명한 stop gradient와 predictor h의 역할 관련 동작 원리의 flaw 를 찾아 반박함.
• representation vector 를 central / residual component 로 decompose 하여 분석함.
• gradient 를 collapse 에 영향을 주지 않는 basic gradient 와 collapse 를 막는 extra gradient 를 나누어 분석함.
• InfoNCE 에서도 de-correlation 과 de-centering 를 찾아, 기존 SSL 방식과 SimSiam 방식 간의 gap 을 bridge 함.
• predictor 구조를 simplify 함으로써 위 결과를 뒷받침함.

첫.. 익일 퇴근
그렇지만 재밋다