[Paper Review] Inductive Representation Learning on Large Graphs

이재헌·2023년 2월 24일

Paper Review

목록 보기

30/37

Inductive Representation Learning on Large Graphs

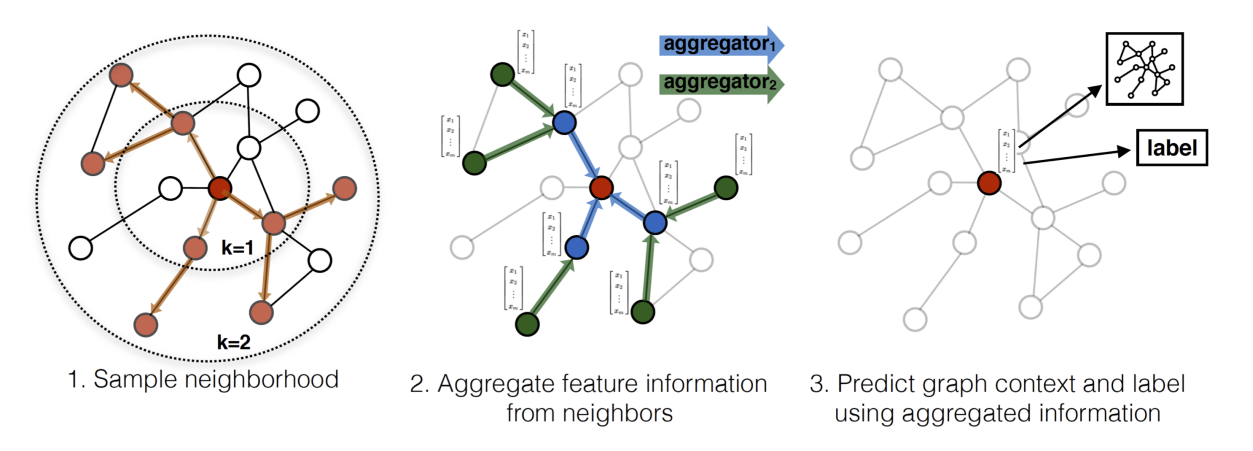
바로 이전 포스팅에서 다뤘던 대표적인 spectral method 인 GCN 는 edge 정보를 표현하지 못하고, scalable 하지 않다는 단점이 있었다. Message Passing Neural Networks (MPNN) 과 Graph Attention Networks (GAT) 는 edge feature 도 고려한 GNN architecture 를 사용한다. 그럼에도 node feature vector 는 entire neighbourhood 에 dependent 하기 때문에 아예 처음 본 graph 에 대해서는 적용이 불가능하다는 한계점이 존재한다. 이를 극복하기 위해 general inductive framework 인 GraphSAGE 가 등장한다. 이 방식은 지금까지도 쓰이는 graph 쪽 대표적인 논문이다.

Introduction

기존 방식 문제점

only applied on fixed graph
do not naturally generalize to unseen data

Present work

GraphSAGE (SAmple and aggreGatE)
inductive node embedding
learn the topological structure of each node's neighborhood
distribution of node features in neighborhood
instead of distinct embedding vector for each node, train aggregator functions
design an unsupervised loss which could be simply replaced by supervised loss

Proposed method: GraphSAgE

핵심 아이디어는 how to aggregate feature information from a node's local neighborhood 에 있다.
특히 K개의 aggregator function $AGGREGATE_k$ 와 그에 따른 weight matrices $W^k$ 는 각각 k번째 search depths 또는 k번째 다른 layer of model 에 propagate information 한다.

Embedding generation (i.e., forward propagation) algorithm

다음은 가장 핵심인 알고리즘이다.

처음에 알고리즘만 보고 $AGGREGATE_k$ 에 대한 감이 안와서 코드를 찾아보았다. 요약한 내용은 다음과 같다.
1) input 에 대해, hop (depth) 개수 만큼 loop 돌기
2) 각 loop 에서 target node vector는 weight 에 통과 후 저장
3) 각 loop 에서 target node 의 neighbor node vector 도 weight 에 통과 후, aggregation 후 weight 에 통과 후 저장
4) 저장된 두 vector 를 concatenation 후 저장
을 iteration 해서 마지막 1x32 vector 를 node 마다 계산하는 과정이다.

setting: two layer setting, K=2

위 그림은 아래 블로그를 참고했다.
출처: https://antonsruberts.github.io/graph/graphsage/

이 때, full neighborhood set을 사용하는 것 대신, computational footprint 를 각 batch 마다 일정하게 고정하기 위해서, 각 iteration 마다 different uniform sample 을 사용하였다.

Learning the parameters of GraphSAgE

fully unsupervised learning setting 에서 predictive representation 을 얻고자 다음과 같은 loss 를 사용했다.

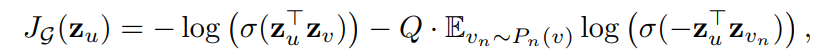
이 때, 오른쪽 항 $P_n(v)$ 는 negative sampling distribution, Q 는 number of negative sample 이다. nearby node 간은 similar representation, disparatenode 간에는 highly distinct 할 것이라는 가정을 담고 있다. (흠..)

model output 이 각 node 에 대한 feature vector 이기 때문에, unsupervised leanring 이 아니라 downstream task 등에서 fully supervised learning setting 방식을 이용해야 할 때, 단순히 loss 만 cross-entropy loss 등의 task-specific objective function 으로 바꿔주면 된다.

Aggregator Architectures

algorithm 에는 $AGGREGATE_k$ 라 표현되어 있던 function 을 4가지 사용해서 비교 실험한다. graph data 에서는 node 간의 sequence 및 structure 가 중요하기 때문에, 이상적으로는 aggregating 하는 과정이 permutation invariance (논문에서는 symmetric) 해야 한다.

Mean aggregator (mean and GCN)

가장 기본적으로, 계산된 vector ${h_u^{k-1}, \forall u \in N(v)}$ 의 elementwise mean 을 취하면 mean aggregator 이다.

GCN aggregator

이를 변형하여, target node 와 $h_v^{k-1}$ 이웃 node ${h_u^{k-1}, \forall u \in N(v)}$ 를 concatenation 후 weight 를 씌우는 방식은, 기존 graph convolution 과 닮아있다.

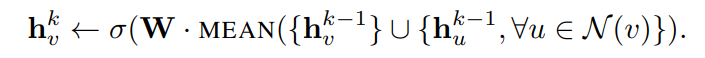
하지만, 기존 graph convolution 은 이전 hop 을 포함한 각 hop 을 concat 하는 방식이기에, 이전 버전과 명확히 다르고, 오히려 이는 "skip connection" between the different search depths or layers 라고 표현한다. (끄덕끄덕)

LSTM aggregator

aggregation 과정에서 RNN (LSTM) module 을 사용한 방식이다. 이는 larger expressive capability 를 가졌다는 장점이 있지만, not inherently symmetric 하다는 문제가 있다. (not permutation invariant) - 이는 어떤 방식에서든 bias 가 발생할 구실을 제공한다.

Pooling Aggregator

4번째 마지막 aggregator 는 trainble 하면서도 symmetric 하다. 다른 방식과는 다르게, aggregation 전에 각 이웃노드에 대해서 weight 를 통과 (MLP 통과) 시키고, elementwise 하게 max operation 을 취한다.

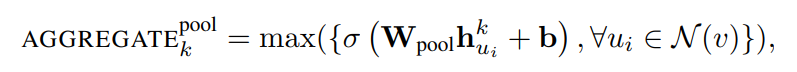
이는 모델로 하여금 효율적으로 neighborhood set 의 different aspect 를 잡아내게 끔 한다. 또, max operator 대신 mean operator 도 사용해보았지만 no significant difference 를 보였다고 한다.

Experiments & Results

다음 세가지 데이터셋에서 실험하였다.
1) classifying academic papers into different subjects using the web of sicence citation dataset
2) classifying reddit posts as belonging to different communities
3) classisfying protein functions across various biological protein-protein iteration (PPI) graphs

속도 면에서도 GraphSAGE 를 사용했을 때 월등히 효율적이었다. DeepWalk 보다 100-500x 빨랐다.
GraphSAGE variants 에서 K=2 setting 은 10-15%의 성능개선을 보였지만, 그 위로 넘어가면 갈수록 marginal return 과 함께 prohibitvely large factor of runtime 을 기록하였다.

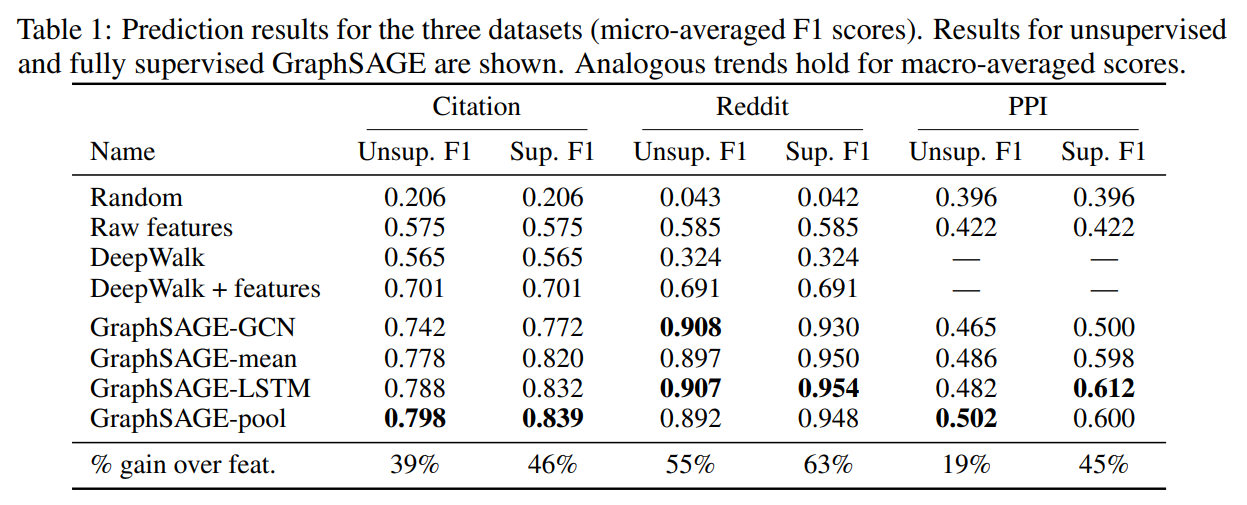
전반적으로, LSTM- and pool-based aggregator 방식을 차용한 모델에서 높은 성능을 보였다. 이 두 모델에 대해서 더 정량적인 평가를 위해 다른 aggregator 방식과 Wilcoxon Singed-Rank Test 를 진행했고, T-statistic 과 p-value 를 기록하였다. LSTM-, pool- aggregator 모두 GCN-based approach 와 비교했을 때, T=1, p=0.02 통계적으로 유의한 결과를 얻었다.

Theoretical analysis

이번 섹션에서는 GraphSAGE 가 얼마나 graph structure 를 잘 배우는지 확인하기 위해 expressive capability 를 탐색하였다. 그 방식으로, clustering coefficient of a node 그 중에서도 the proportion of triangles that are closed within the node's 1-hop neighborhood 로 확인하였다. 그리고 다음 Theorem을 증명하였다.

위 Theorem 은 어떤 graph 에 대해서, Algorithm 1 의 parameter setting이 존재하는데, st 이는 모든 node 의 feature 가 다르다는 가정하에, approximate clustering coefficient to an arbitrary precision 이 가능한 setting 이다.