[Paper Review] Interpretable Deep Neural Network to Predict Estrogen Receptor Status from Haematoxylin-Eosin Images

JaeHeon Lee, 이재헌·2022년 4월 7일

Digital Pathology XAI paper-review survival analysis

Paper Review

목록 보기

5/49

Interpretable Deep Neural Network to Predict Estrogen Receptor Status from Haematoxylin-Eosin Images

Deep Neural Network에서의 explainability와 관련된 논문이다. Explainability는 특히 survival analysis에서 중요할 것으로 생각되어 논문에 소개된 방법 이외에도 적극적으로 찾아 공부할 예정이다.

Introduction

Breast cancer에서 estrogen receptor (ER) status는 치료법과 직결되기 때문에 이를 파악하는 것은 큰 clinical importance를 지닌다. Immunohistochemistry (IHC) staining으로 파악이 가능하지만 비싸다. 최근 연구 결과 morphological feature가 H&E slide에서도 발견됨이 확인되어 DNN을 통한 연구가 이루어졌지만, 어느 feature가 의사결정에 결정적인 역할을 했는지 파악하기 어렵다.

이 논문에서는 end-to-end deep neural network ensemble을 pooled random patch로 train 시켰고, validation data에 근거하여 low confidence score를 가지는 sample은 reject함으로써 좋은 성능을 거두었다. 또한 end-to-end learning일수록 모델의 interpretability가 떨어진다는 점을 완화하기 위해 relevance heatmaps of model prediction 을 분석하였다.

Method

Data and Preprocessing

데이터는 TCGA-BRCA을 사용했다. color normalization, sparse stain separation을 통해 staining 과정의 variability를 설명하고자 하였다. ER status에 대해 702개가 라벨이 달렸고, 그 중 176개가 ER-, 526개가 ER+이다. Grading(tumor grade)에 대해 총 469개 중 272개가 low grade(G1, G2), 197개가 high grade(G3)로 달렸다.

Traning and Evaluation

다른 논문에 비해 모델의 설명이 자세하지 않았다. 설명은 다음과 같이 요약해 볼 수 있다.

ensemble, 끝 1/4이 잘린 ResNet18 구조의 transfer learning
64 x 64 px의 patch가 256-d feature vector로 encoding됨.
각 feature vector은 fused by averaging over the patches
dense layer with two output dimension and softmax activation

Visual Explanation of ER Status Predictions

Layer-Wise Relevance Propagation

LRP는 classification result에 대한 각 input dimension의 기여도(contribution)를 설명하는 score를 계산한다. 다시 말해, relevance score를 output에서 input 방향으로 input dimension에 재분배한다. 핵심 가정은 다음과 같다.

\sum_{i} r_i^l \approx \sum_{j} r_j^{l+1}

Total signal $r^{l+1}$ in layer $l+1$ should be approximately equal to total signal $r^{l}$ . 그렇기에 input layer 까지 propagation 되면, 사실상 relevances는 output signal에 대한 decomposition으로 볼 수 있다는 것이다.

\sum_{i} r_i^0 \approx f(x^0)

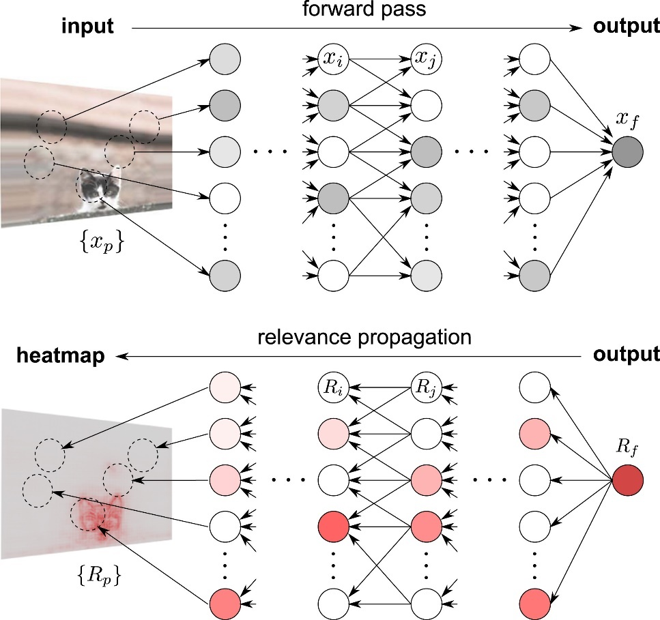
그렇다면 이제 relevance score를 계산하기 위한 방법으로는 무엇이 있을지 궁금하다. Relevance score를 계산하는 "rule"에는 여러가지가 있다. 이 rule을 관통하는 main concept은 relevance score를 입력의 변화에 따른 출력의 변화 정도 로 생각하고, output $f(x)$ 에 대한 각각의 입력 차원들의 기여도를 ${\partial f \over \partial x_i}$ 와의 관계를 통해 정의하는 것이다. 1차 Taylor series를 통해 함수를 근사하고, $f(a)=0$ 을 만족하는 $a$ 를 찾고, 그 지점으로부터 함수를 근사함으로써 $f(x)$ 를 relevance score만으로 분해가능하다.

f(x) = f(a) + \sum_{i=1}^{d} {\partial f \over \partial x_i} (x_i - a_i) + \epsilon

=\sum_{i=1}^{d} {\partial f \over \partial x_i} (x_i - a_i)

= \sum_{i=1}^{d}R_i

이 때 a를 찾는 과정에서 다양한 방법이 사용되고, 다음은 그에 따른 LRP rule의 list이다.

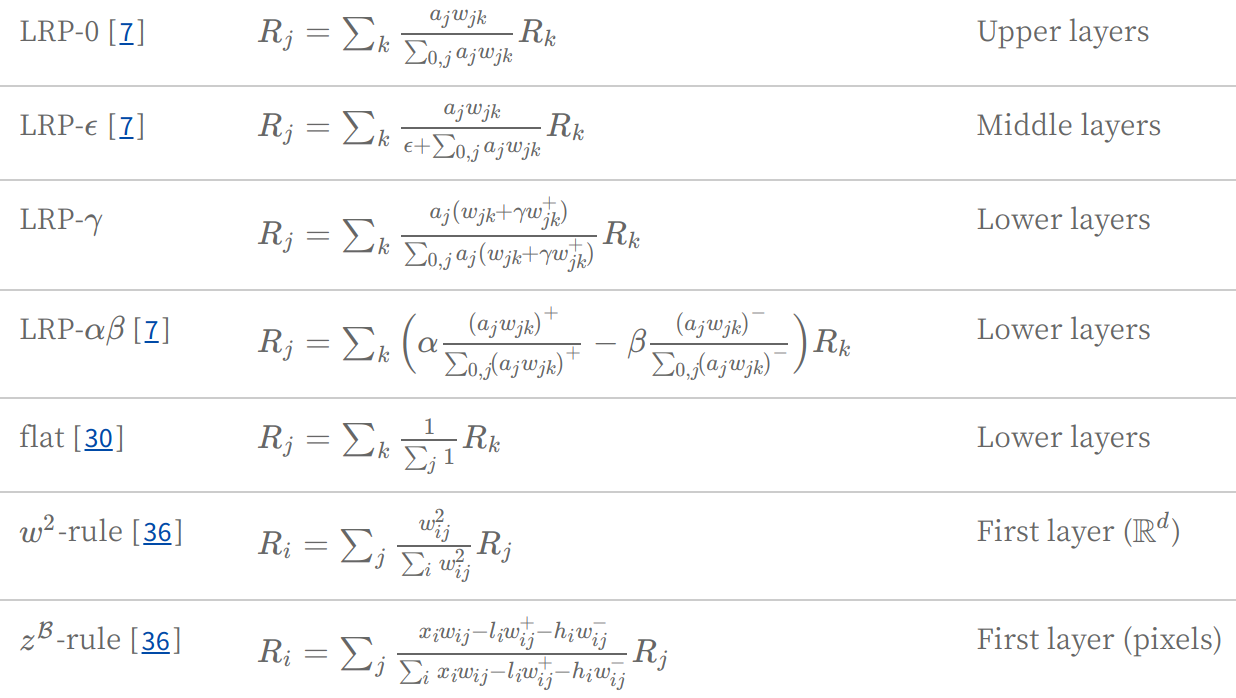
모델 내에서도 쓰임새에 맞게 LRP rule이 적용되었다. Dense layer에서는 $\epsilon$ -rule, Batch Normalization이 적용된 layer에는 $|z|$ -rule, convolutional layer에는 $\alpha$ =1, $\beta$ =0의 $\alpha \beta$ -rule이 사용되었다. 각 rule의 사용 근거는 이 논문의 참고문헌에 언급되어있다.

Experiments & Discussion

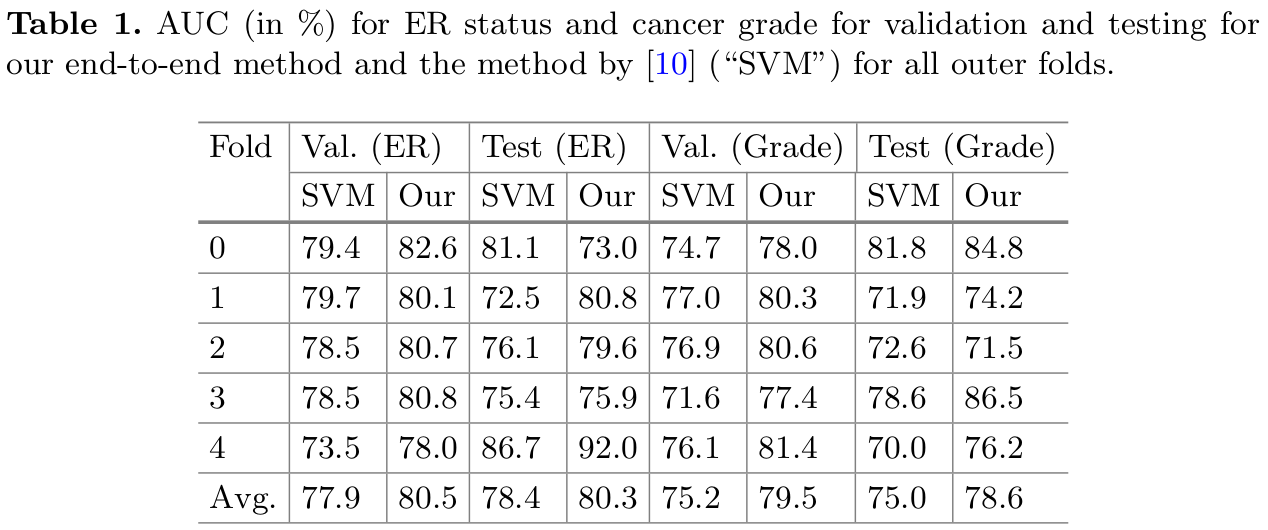
저자는 이 시기에 state-of-the-art로 알려져 있던 Couture의 SVM (with isotonic calibration) 방식과 성능을 비교 분석하였다. Validation set에서 모든 fold에서 더 좋은 성능을 거두었고, test set에서도 괜찮은 성능을 거두었다 해석하였다. 또한 ER status prediction의 test AUC가 CV split마다 0.73 - 0.92로 차이가 있음을 인지하였다.

Rejection options

HE image를 기반으로 한 ER status determination 과정은 추후 IHC stain 등의 검증이 따로 존재하지 않기에 "confidence"를 고려하는 것이 중요하다. 따라서 다른 검증 과정을 거칠 수 있도록 low confidence인 채로 classify된 sample들은 reject 시키는 과정이 필요하다. 저자는 classifier output ("confidence")의 threshold를 validation data를 통해 선정하였다. (보통 DNN은 too optimistic 해서 probability를 confidence로 쓰지 않는데, 이 논문에서는 calibrate 되지 않았음에도 사용하였다.)

조건은 다음과 같다. The precision was maximized while classifying more than 10% of the cases. 다음 기준에 따라 threshold를 선정하였고, 나머지를 reject함으로써 high precision (97%, 94% for val, test)를 얻었다고 설명하였다. (fold 별로 threshold를 선택하는 것이 맞나.. fold 별로 다르게 threshold 매긴 것을 average 내는 것이 맞나...싶긴 하다. 그리고 97%, 94%라는 수치는 어디에서 가져온 것인지 잘 모르겠다..)

Visual Explanation

LRP를 통해 계산한 LRP heatmap의 결과는 다음과 같다. 왼쪽 사진은 LRP에 의한 heatmap, 오른쪽 사진은 비교를 위해 SmoothGrad에 의한 heatmap을 보여주었다. 붉은색은 ER+, 파란색은 ER-, 초록색은 neutral status를 가리킨다.

저자는 다음과 같이 결과를 요약하였다.

Stroma는 ER+의 중요한 indicator이다. 하지만 논란 o -> 더 큰 데이터셋에서 검증 필요...
- 이 가정이 틀린다하더라도, 오히려 explainability가 중요하다는 것을 반증.
Lymphocyte infiltration은 ER-의 indicator이다.
high grade nuclear grade, poor differentiation, mitoses는 ER-의 indicator이다.
모델은 인디언이 서있는 모습의 길쭉길쭉한 pattern에 반응했다. 이는 infiltrating lobular carcinoma에서 나타나는 특징으로, ER+ subtype과 연관되어 있다.
SmoothGrad와 같은 high computational effort가 필요한 method의 결과와 일관된 결과를 보였다.

Conclusion

explainability: 모델의 각 영역마다 다른 rule을 적용한 layer-wise relevance propagation을 통해 LRP heatmap을 계산하였고, cost가 큰 SmoothGrad와 비슷한 결과를 몇몇 tile에서 보여줌.

이 논문에서는 breast cancer의 ER status prediction을 위해 end-to-end 모델을 적용하여 기존 SVM을 사용했던 논문의 결과보다 좋은 성능을 거두었다. Probability를 confidence로 대체해 rejection threshold를 설정함으로써 high precision을 었었다. 마지막으로 explanation heatmap을 계산하여 model intrinsic을 이해하려는 노력을 하였다.

궁금했던 점

probability를 confidence로 써서 rejection을 해도 되는가?
rejection을 해서 나온 precision 결과는 어디서 어떻게 봐야 하는가?
aggregation을 averaging만 했는데도 성능이 왜 잘 나오는 것인가..
explainability의 성능..은 어떻게 정량적으로 측정할 수 있을 것인가?

참고:
https://link.springer.com/chapter/10.1007/978-3-030-28954-6_10 (LRP rule list)
https://angeloyeo.github.io/2019/08/17/Layerwise_Relevance_Propagation.html (LRP)
https://arxiv.org/abs/1512.02479 (LRP)
https://www.nature.com/articles/s41523-018-0079-1 (Couture2018)

JaeHeon Lee, 이재헌

https://jaeheon-lee486.github.io/

이전 포스트

[Paper Review] Self-supervised learning improves dMMR/MSI detection from histology slides across multiple cancers

다음 포스트