The Simplicity Bias in Multi-Task RNNs: Shared Attractors, Reuse of Dynamics, and Geometric Representation

• How can a single neural population combine these disparate objects (dynamical motifs) into a joint representation? And under what conditions do these representations become shared or separate?
• simplicity bias: the author wasn’t trying to quantify; they were just pointing out such tendency.
  • persists regardless of the number of tasks or the nature of the dynamical objects
    ( observed in various objects including fixed points, limit cycles, line- plane- attractors)
  • link this bias to “sequential emergence” of attractors
  • how external factors can resist this bias and create more complex dynamic objects
    → this external factors means, ‘architectural constraints’ ~ gated, orthogonal, parallel
• They use “separate” input and output
  

• In this settings, they have

  • gated setting: only one task in a time, no output in other task
    • in code, they ignore loss from other tasks
  • orthogonal setting: only one task in a time, zero output in other task
  • parallel setting: multiple tasks in a time, no constraint in other task

• Compared to gated settings, orthogonal and parallel setting allow ‘interaction btw tasks’

• task examples
  - from the top, fixed point, limited cycles, line-, plane- attractor (left) and attractors (right)
  

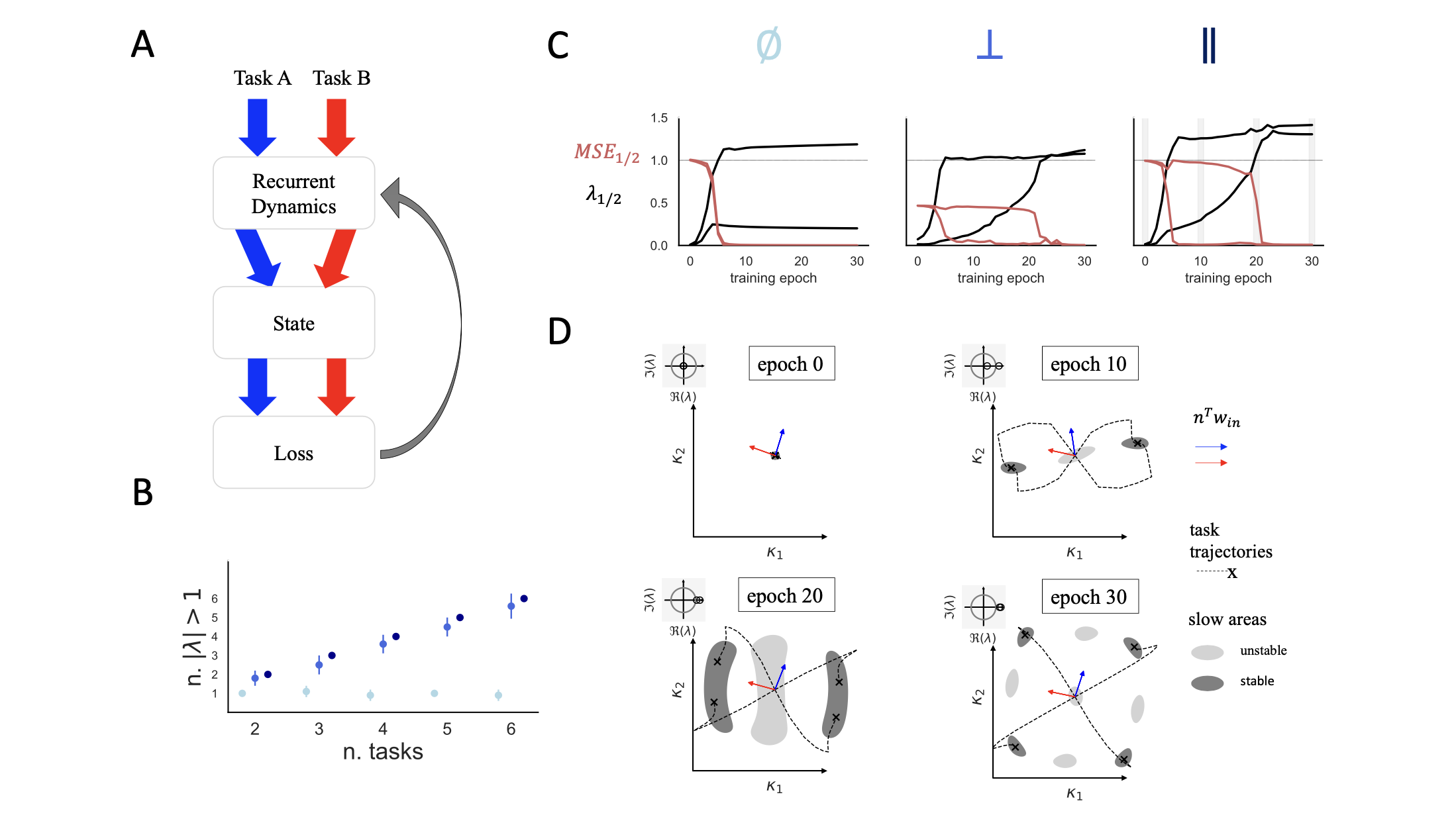
• They trained two tasks in gated mode (sky blue) and orthogonal mode (blue)
  

• Especially in gated mode, they tend to share the attractors — simplicity bias (why? below)

  • A : gated mode resulted in a complete overlap between the tasks (even diff tasks), the opposite with orthogonal settings
  • B: linear classifier to separate the neural trajectories (2) — failed in gated, success in ortho
  • C: ratio variances between and within tasks (F-factor) — shared in gated, separated in ortho
  • D: when we look at the spectrum of connectivity matrix (W_recurrent) - lambda
    • the number of unstable eigenvalues was larger in the orthogonal settings
    • oh, in orthogonal settings, there are multiple fixed points! hey then how it emerges???

• Next question is, what is the origin of this simplicity bias??

• consider the two task needs two fixed points each (4 points)

  • In Gated mode: 2 shared 2 shared
    • the recurrent dynamics cause the states to mostly depend on the “task agnostic attractors”, and less on the task-specific inputs
  • In orthogonal mode: 4 all different
    • two attractors have to be orthogonal to each other, forcing the network to separate them
    • because the network architecture make the other zero when one is training

• ok let’s track this hypothesis by following the attractor landscape of networks (low-rank) [13]
  

• with this projection (approximation), they followed the evolution of the dynamics in parallel settings trained on two fixed-point tasks
  

• in C and D,

  • at epoch0 only origin is stable. (two eigenvalues are in unit circle)
  • origin destabilizes, single unstable eigenvalue emerges
  • more training, second eigenvalue leaves the unit circle → pair of stable fixed points emerges

• in B, they repeated this analysis. (skyblue, blue, darkblue - gated, ortho, parallel)

  • in orthogonal, parallel mode, we can see the clear sequential emergence of two outliers
  • the gated setting is solved with a single outlier, as all tasks share a common attractor

In dicussion,

• reusing existing representation leads to faster learning of task ~ i think they wanted to mention the "efficiency" as shown in gated setting
• if there're modular representation, it could be some constraint on architecture. good point! since in typical multitask learning setting, the 'rule' signals are separately processing at the head of the RNN..
• an attractor shared btw tasks is not identical to an attractor that was formed in response to a single task so if one task has oscillatory component, it might suggest that the same circuit is also capable of generating such oscillation in another context. (?!?)