A complexity-based theory of compositionality

Compositionality is fundamental to intelligence. espeically in human, the structure of thought, language, higher-level reasoning. however, there's no measurable and mathematical definition of this, so they tried to quantify this with algorithmic information theory, Kolmogorov complexity.

Definition 1 (compositinality)

• existence of a symbolic complex expression -> where do these expressions saved? in human, they're saved in "language" or other kinds of expression but in neural network it could be only exist by some combination of representations.
• similarly, the structure of expression (somehow language) is also unclear
• in language, there's no limit on mapping the sentence and the semantics.
• also the semantics varies in what context that the sentence is located.

compressing a representation, Kolmogorov complexity

• through the lens of optimal compresseion and Kolmogorov complexity
• kolmogorov complexity defines a notion of information quantity
  :length of the shortest program in some programming language that outputs that object
  ex) KC of 101010: length(repeat 10, 3 times)
  : the more it has structure or pattern the small value of kolmogorov complexity that object get
  

• in the context of ML, given dataset X = (x1, ,,, xn) sufficiently large drawn iid from dist p(x)
• the optimal method for compressing :let's say K(X) = K(X|p) + K(p)
• then K(X|p) can be optimally encoded using only $-log_2p(x_i)$ bits Shannon information
• second term K(p) refers to complexity of the data distribution

Compressing $Z$ as a function of parts

• denote a representation by a matrix $Z \in {\R}^{N \times D}$ where each row $z_n$ is D-dimesional vector from $p(z|x)p(x)$.
• describe a representation using short parts-based constituents sentences $W \in \mathcal{V}^{N \times M}$ where nu is finite set of discrete symbols to vocabulary where M is maximum sentence length.
• let's say $p_w(w)$ is their most compressed forms
• then we can say like below

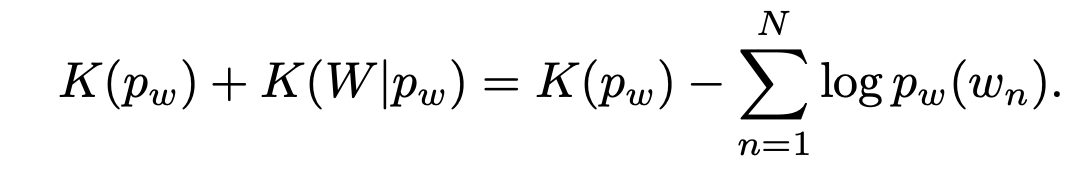
• then for the representation decoding from their sentences, we need new mapper $f:\mathcal{V}^{M} - \R^D$ : semantics
• one thing important about K(f), set p with Normal distribution, and introduced additional error term induced by Gaussian assumption -> thats K(Z|W,f)

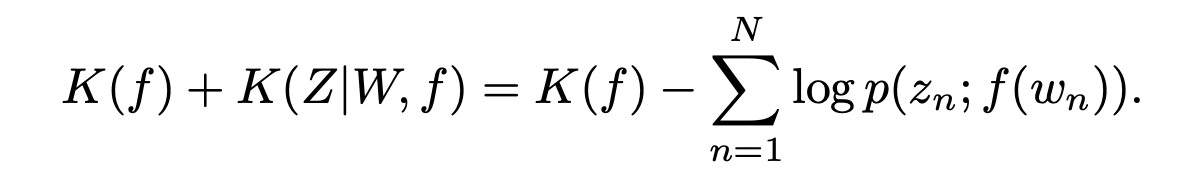
Summary and further intuition

• total Kolmogorov complexity of the representation:

• Representational compositionality: a formal definition of compositionality

wip