[딥러닝] Convolutional Neural Networks Week 1

출처 : https://www.coursera.org/specializations/deep-learning

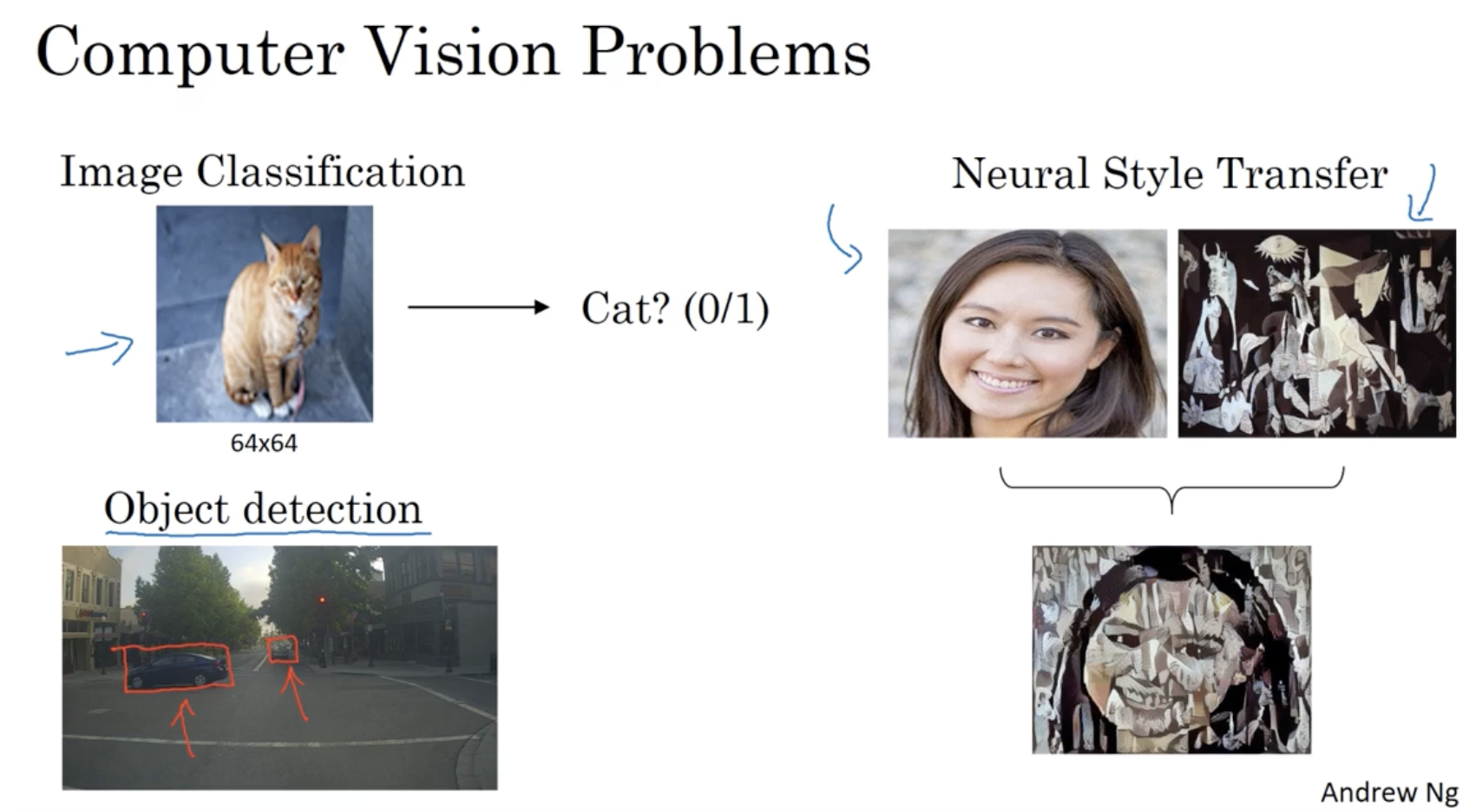
컴퓨터 비전 연구의 예시는 아래와 같다.

• 이미지 분류
• 객체 탐지
• 스타일 변환
• ...
  

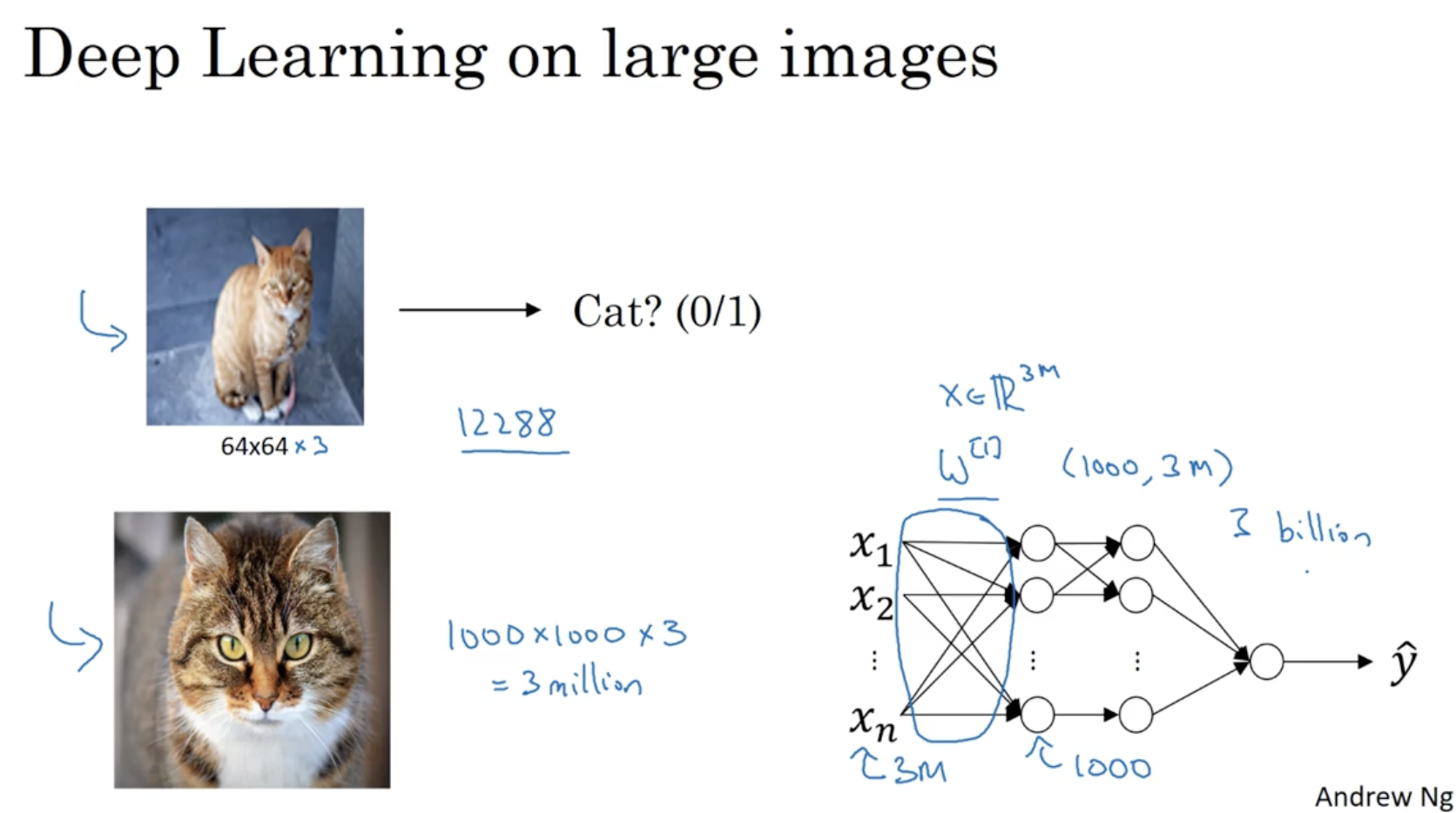
하지만 일반적인 딥러닝 모델을 가지고 이미지 데이터를 처리할 때 아래와 같은 제약이 존재한다.

• 작은 사이즈의 이미지 데이터에 대해서는 괜찮다. 예를 들어, 64 x 64 이미지에 대해서는 64x64x3 개의 feature가 존재하고, $x\in\mathbb{R}^{12288}$이 된다. feature의 차원이 크긴 하지만 나름대로 계산할 수는 있다.
• 하지만 이미지 사이즈가 1000 x 1000이라면 얘기가 다르다. 이 경우, feature의 차원은 3M이 되며, 이를 학습하는 파라미터 $W^{[1]}$의 차원은 ${(\text{$ \# of$ hidden units }, 3M)}$이 되어, 총 3B개의 파라미터가 나올 것이다. (메모리 상 한계가 있을 것이다.)
• 따라서 이를 위해 Convolutional Neural Networks (CNN) 모델이 나오게 된다.
  

---

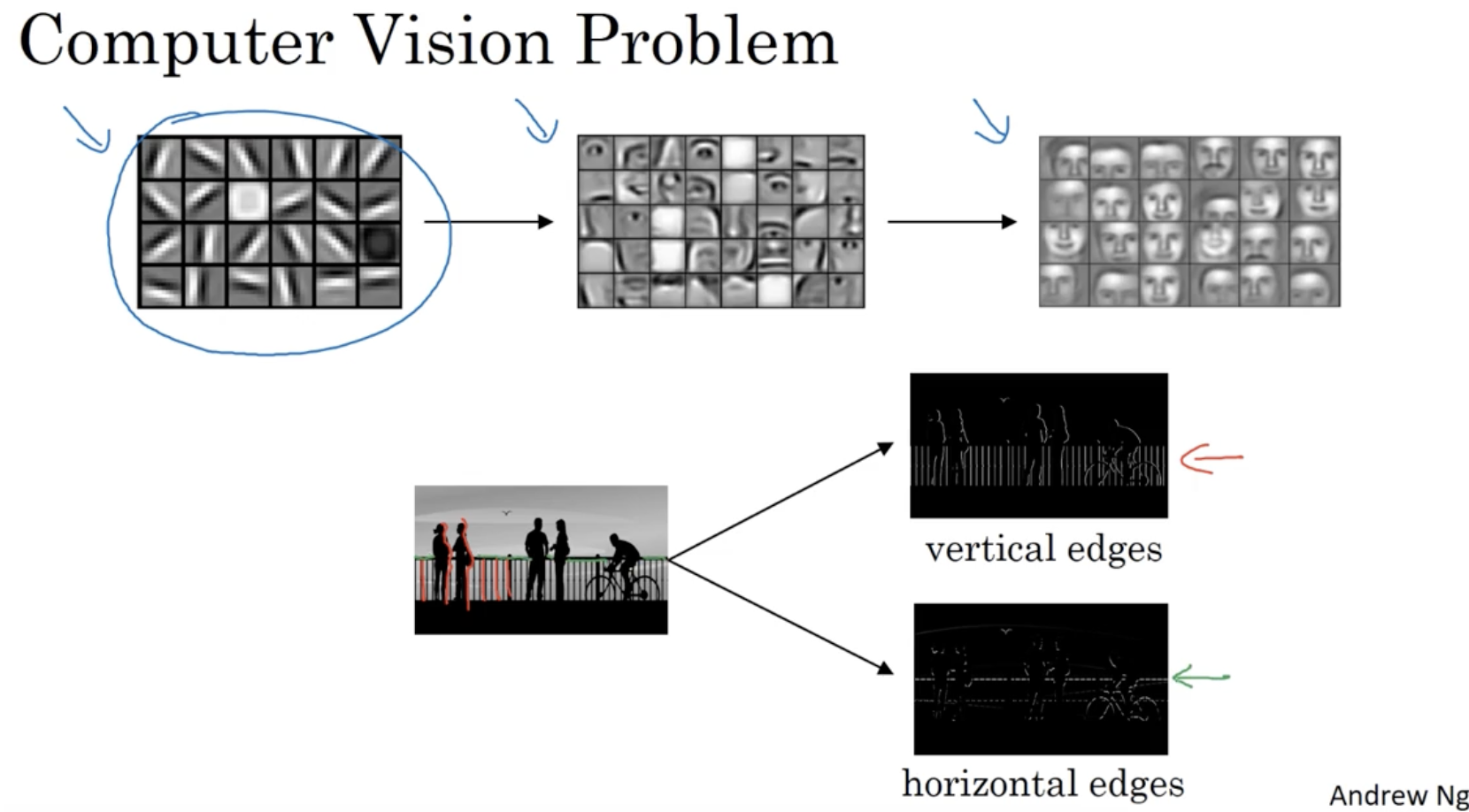
따라서 고차원 데이터에 대해서 처리할 때, 먼저 edge detection 을 적용해줘야 한다.

• 예를 들어 이미지에서 vertical(수직) edge와 horizontal(수평) edge를 추출한다.
  

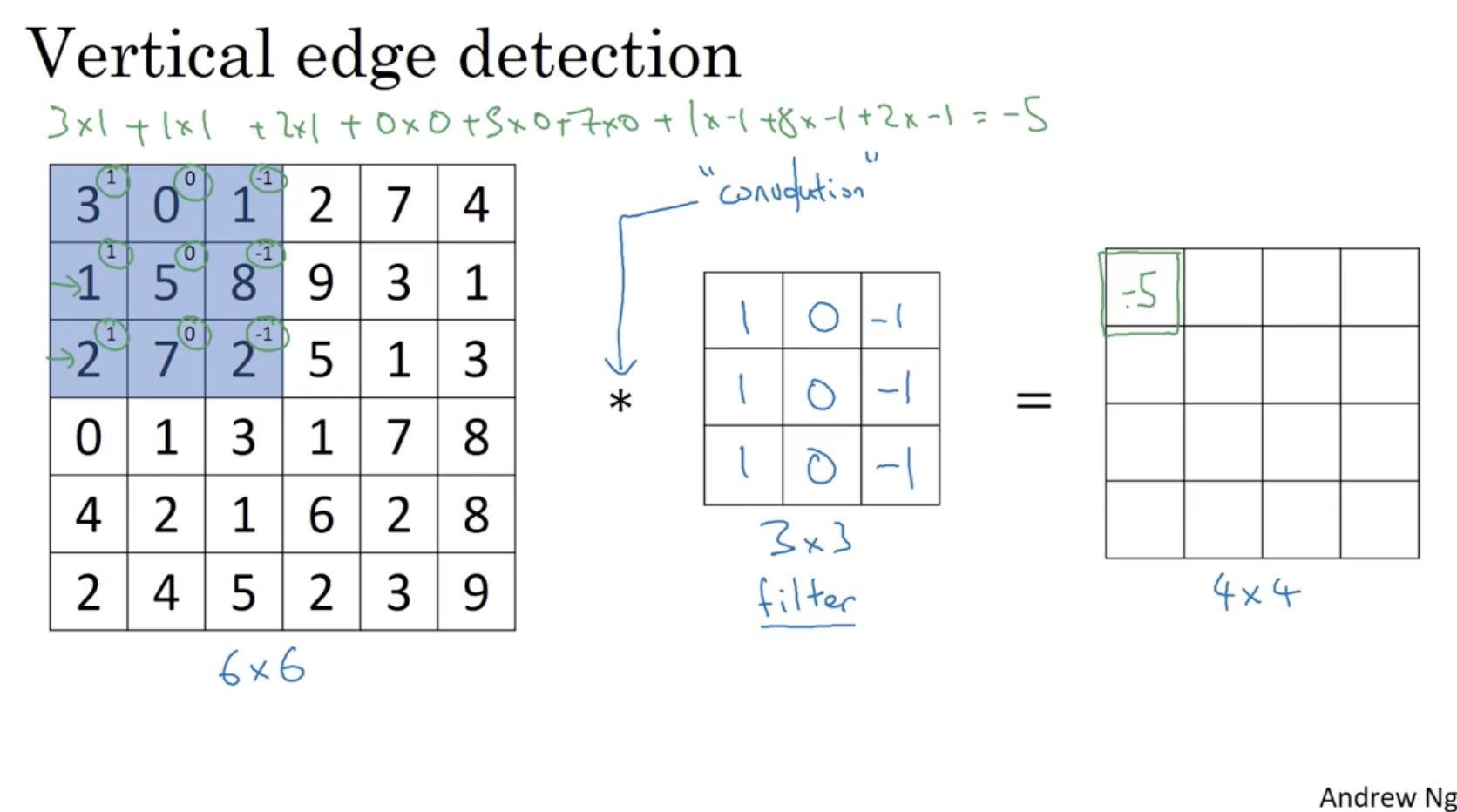
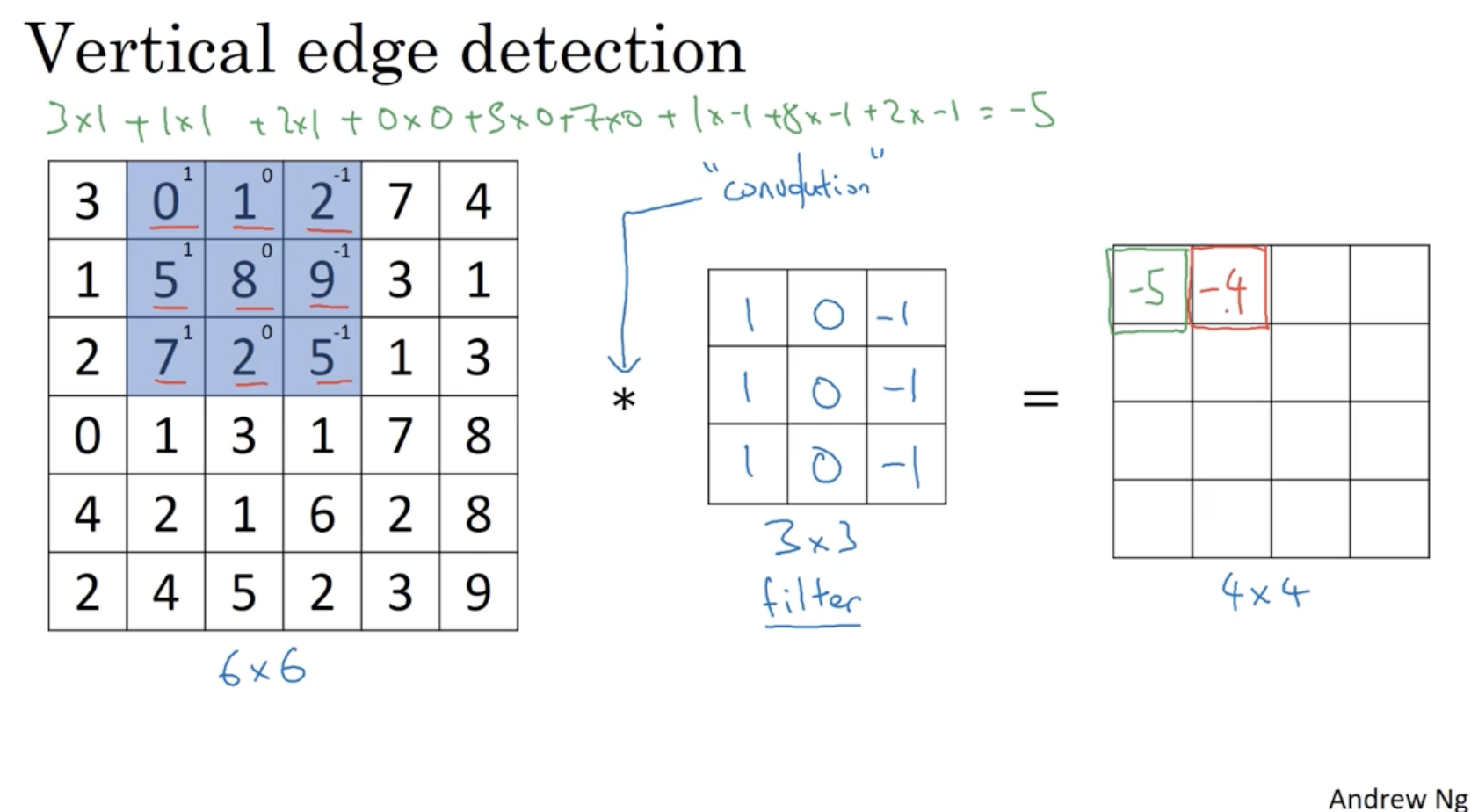
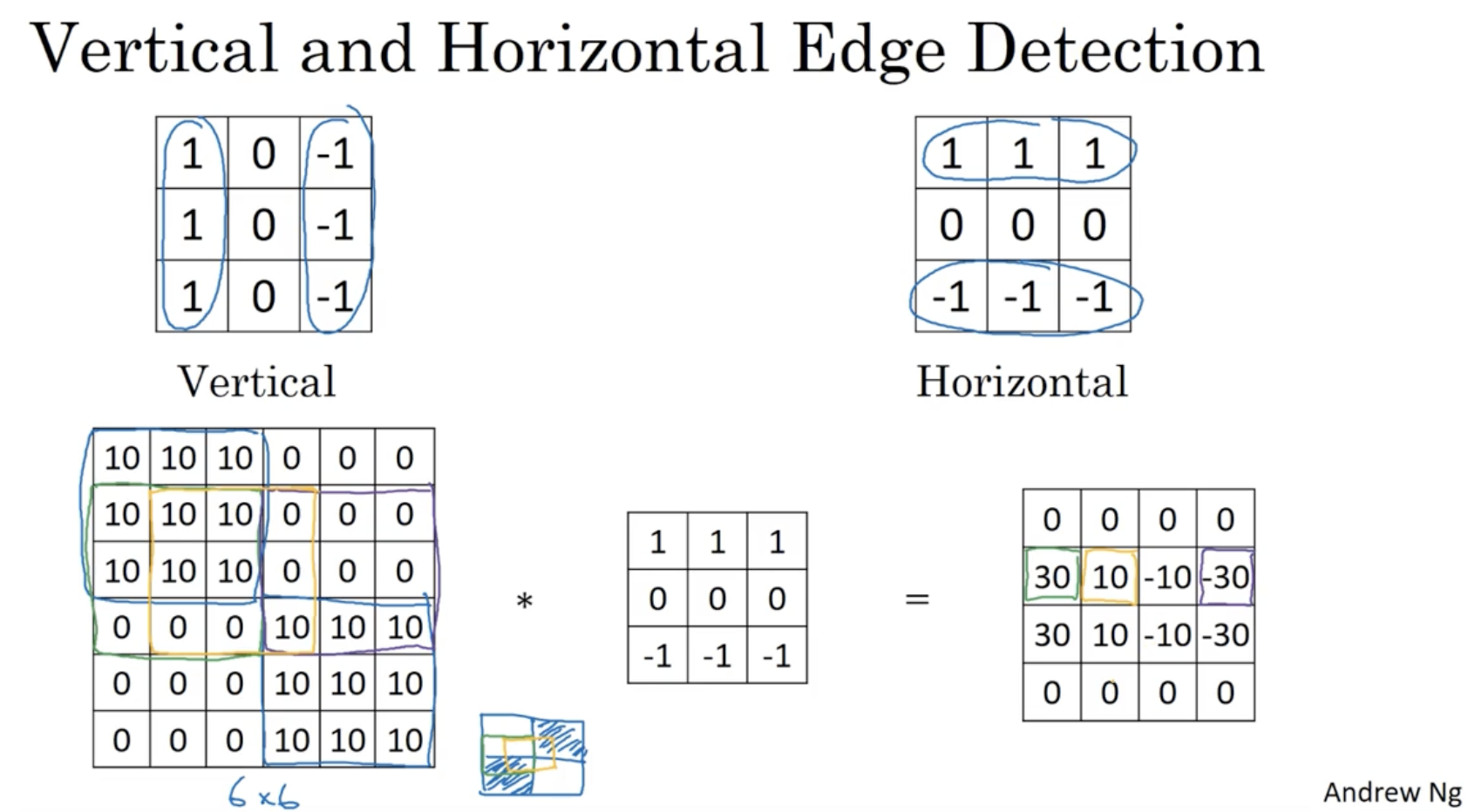
vertical edge detection의 방법은 아래와 같다.

• 좌측처럼 gray scale(no RGB($\mathbb{R}^{1\times 3}$), only Bright or Dark($\mathbb{R}^{1\times 1}$) $6\times 6$ 이미지 데이터가 주어졌다고 해보자.
• 여기에 중간과 같이 좌측 열은 1, 중간 열은 0, 우측 열은 -1인 $3\times 3$ filter(kernel)를 적용하여 이미지 데이터와 convolution 연산을 수행한다. (like element-wise product)
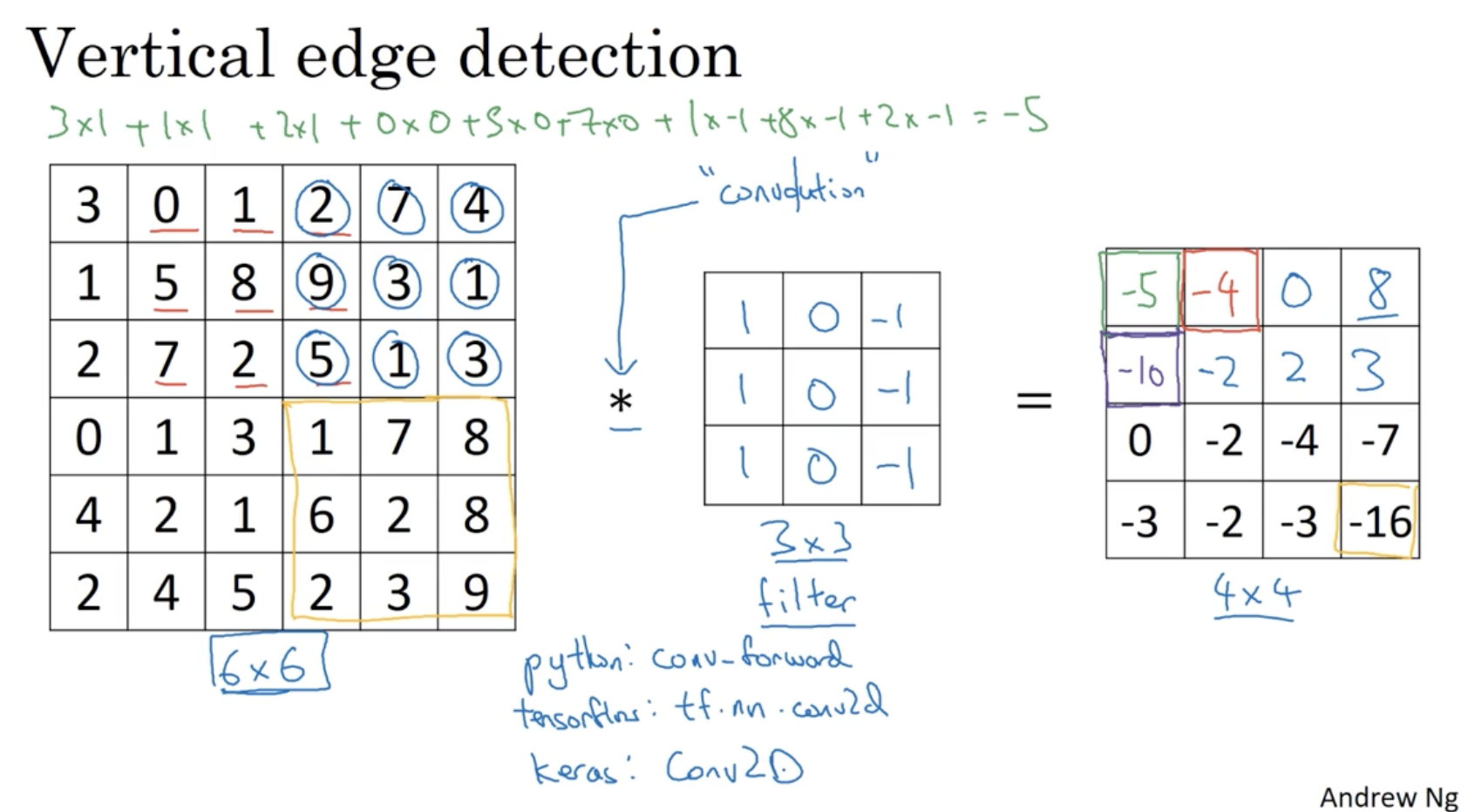
• 그러면 우측과 같이 $4\times 4$ 행렬이 만들어질 것이고, 이 행렬이 기존의 $6\times 6$ 이미지의 vertical edge 정보를 포함하고 있을 것이다.
  
  
  
• 라이브러리 및 프레임워크마다 이를 구현하는 코드명이 약간씩 다르다.
  • python : conv_forward
  • tensorflow : tf.nn.conv2d
  • keras : Conv2D

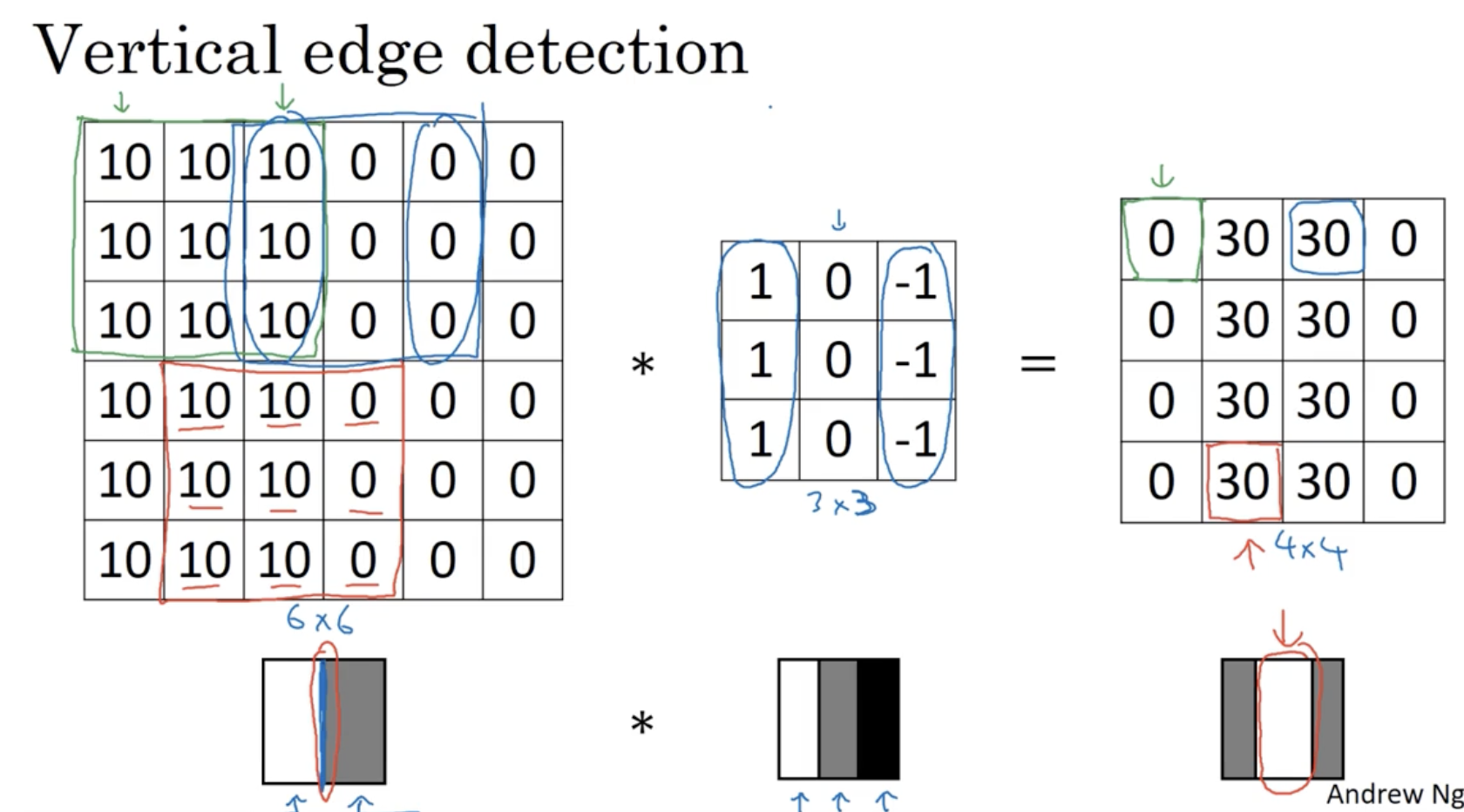
아래 예시를 보자.

• 좌측은 흰/회 의 gray scale 데이터이다. 이 데이터의 vertical edge detection를 해보자.
• 중간과 같이 filter가 존재한다. 이 필터는 백/회/검 을 의미한다.
• 그리고 filter convolution를 적용하면 우측과 같이 edge에 해당하는 원소들의 값을 구할 수가 있을 것이다.
  

---

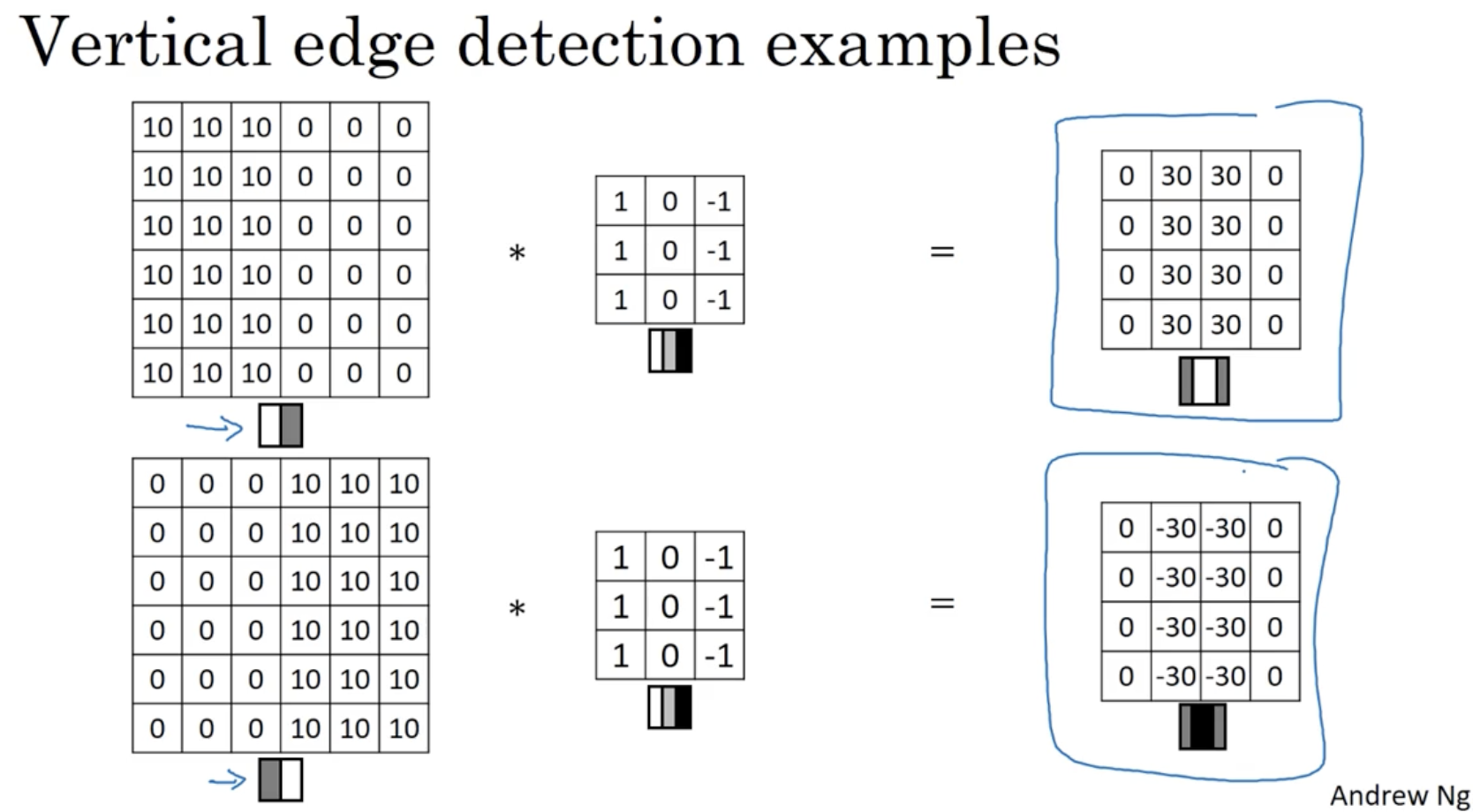
그러면 데이터를 반전시킨 후 필터를 적용하면 결과는 어떻게 나올까?

• 아래와 같이 edge에 해당하는 원소값들의 절댓값에는 변화가 없다.
• 따라서 만약 밝거나 어둡거나에 신경을 쓰지 않는다면 그저 절댓값을 취해도 괜찮을 것이다.
  

그리고 vertical(수직) edge detection이 아닌 horizontal(수평) edge detection도 방법은 같다.

• 아래와 같이 필터를 수평적으로 분리해서 적용하면 (행을 구분하여 적용하면) horizontal edge detection이 된다.
  

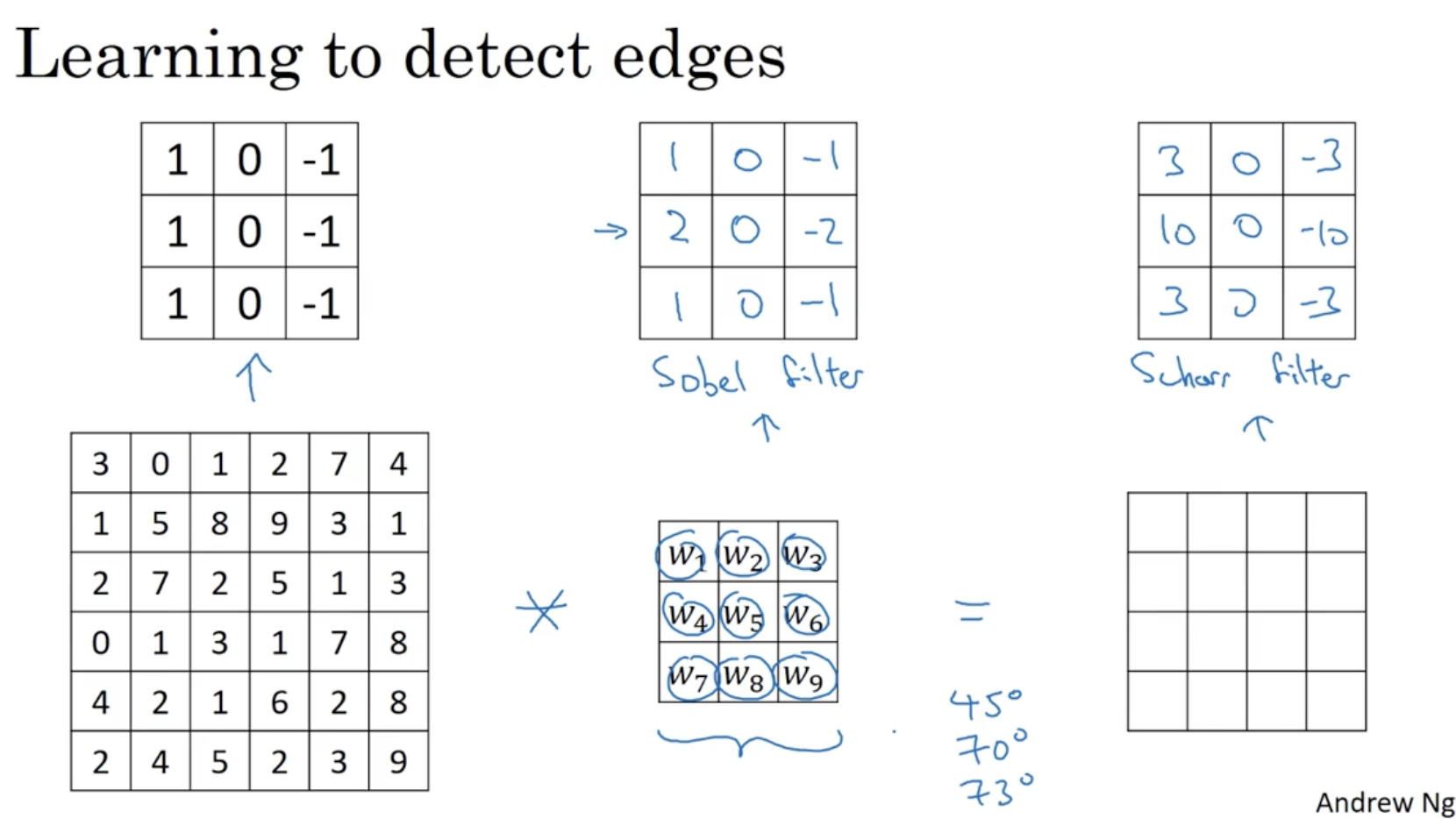
그리고 edge detection의 filter를 학습시킬 수도 있다.

• 아래와 같이 고정적인 필터값 sobel filter or scharr filter를 적용시켜도 되지만,
• filter의 값을 w 파라미터로 두어 이를 원하는 대로 학습시킬 수도 있다. (예를 들어 45도 기준의 대각선 위주의 edge detection, 70도 기준의 ... 등)
  

---

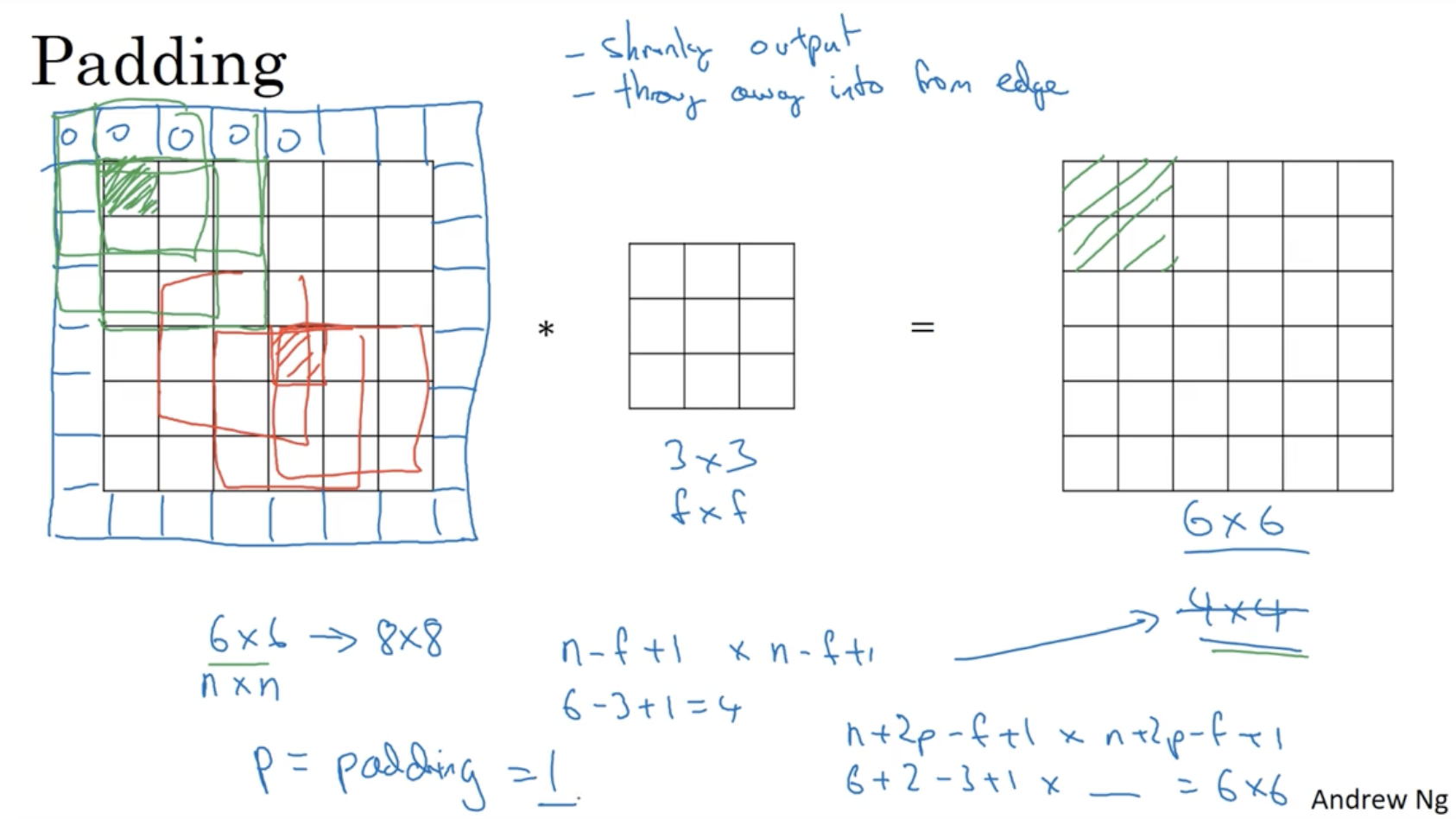
다음으로 padding 이라는 개념을 알아보자.

• 이전처럼 original $6\times6$ 이미지에 $3\times 3$ 필터를 convolution하면 그 결과가 $4\times 4$로 나온다.
• 이 경우 아래 좌측 행렬의 초록색 원소의 값은 빨간색 원소의 값보다 반영률이 적을 것이다.
• 또한 입력 이미지의 크기가 달라진다는 점도 존재한다.
• 따라서 이를 방지하기 위해 padding 이라는 개념을 도입하였다.
• padding은 다음과 같다.
  • 아래 좌측 행렬과 같이 $p=1$ 사이즈의 padding을 추가한다. (이 예시에서는 원소의 값을 0으로 채운다.)
  • 그러고 나서 padding이 적용된 $8\times 8$ 이미지에 $3\times 3$ 필터의 convolution 연산을 하면 우측과 같이 $6\times 6$ 행렬이 나올 것이다.
  • 즉, 기존 이미지의 크기를 $n \times n$, filter의 크기를 $f \times f$, padding의 사이즈를 $p$라고 했을 때,
  • padding이 적용되지 않을 경우 출력 행렬은 $(n - f + 1) \times (n - f + 1)$ 크기를 갖지만,
  • padding을 적용할 경우, 출력 행렬은 $(n + 2p - f + 1) \times (n + 2p - f + 1)$ 크기를 가질 것이다.
    

따라서 padding의 유무에 따른 convolution을 정리하면 다음과 같다.

• "Valid" convolution : no padding. output matrix : $(n - f + 1)\times(n - f + 1)$
• "Same" convolution : with padding. (input matrix의 사이즈 = output matrix의 사이즈)
  • input matrix : $n \times n$
  • output matrix : $(n + 2p - f + 1) \times (n + 2p - f + 1)$
  • 따라서 $(n=n+2p-f+1)$ 수식을 만족하기 위해서
  • $2p-f+1=0$
  • $p=\frac{f-1}{2}$ 이 된다.
  • 그리고 보통 $p$는 홀수값을 갖는다.
    

---

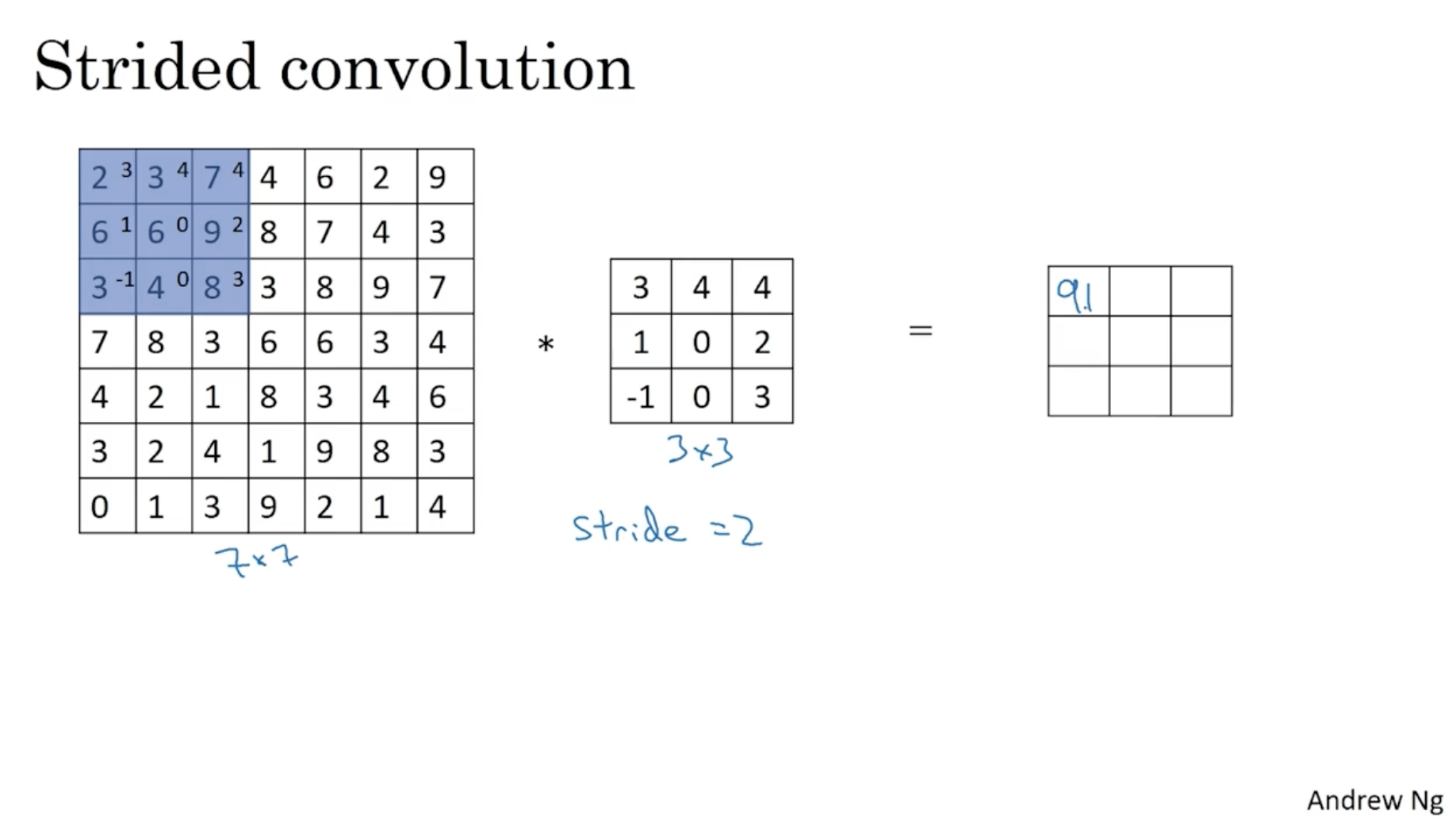
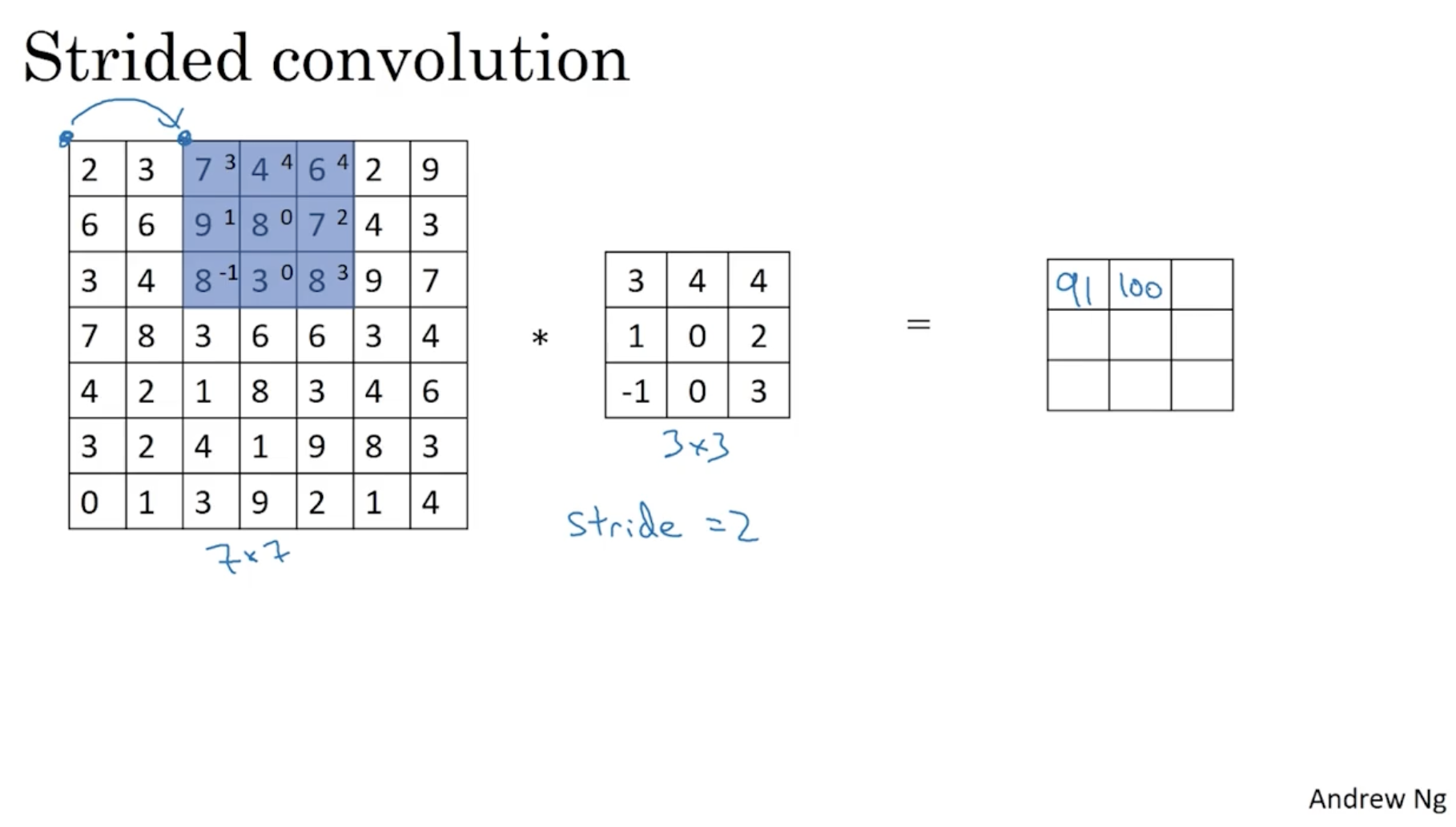
다음으로 Stride의 개념에 대해서 알아보자.

• 아래는 $stride = 2$에 대한 예시이다.
• 보다시피 이전과 동일하게 convolution 연산을 적용한다. 다만, 다음 위치로 넘어가는 Step의 크기가 2씩 증가한다. (이 경우 stride가 2라고 한다.)
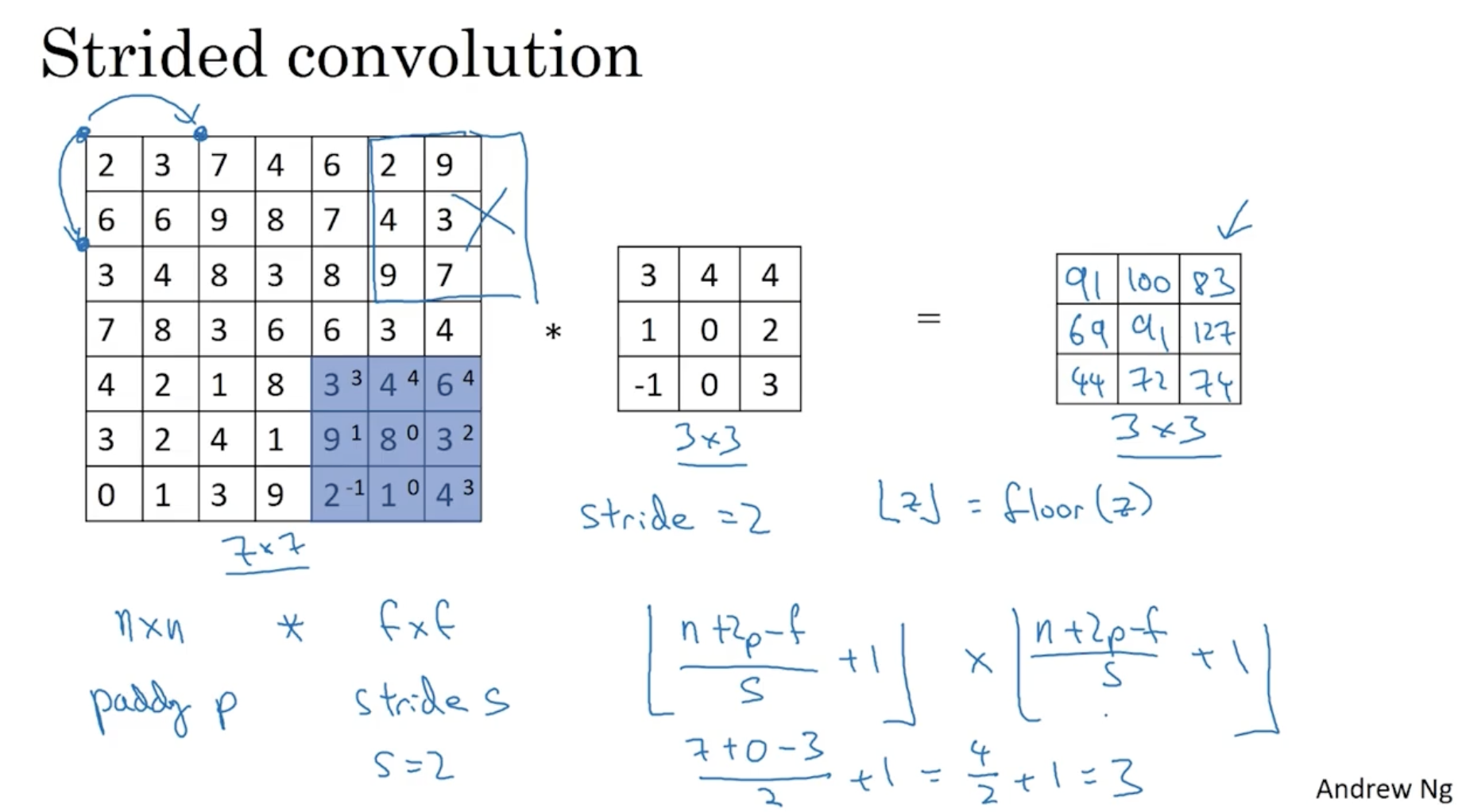
• 따라서 아래와 같이 결과가 나올 것이다.
  
  
  
• stride 크기 $s$가 적용될 경우, 기존의 padding 크기 $p$와 더불어 output matrix의 크기는 다음과 같이 정해질 것이다.
  • $output \ matrix : \lfloor\frac{n+2p-f}{s}+1\rfloor\times\lfloor\frac{n+2p-f}{s}+1\rfloor$
  • 즉, 반내림 기호 $\lfloor \ \rfloor$ 가 적용되어 위 그림과 같이 만약 입력 행렬의 크기가 $8\times 8$ 이었어도 마지막은 적용이 되지 않았을 것이다.

따라서 convolution 연산에서의 Output matrix의 크기를 요약하면 아래와 같다.

• input 이미지 크기 : $n\times n$
• filter 크기 : $f\times f$
• padding 사이즈 : $p$
• stride 사이즈 : $s$
• 위 정보가 주어졌을 때 output matrix의 크기는 다음과 같다.
• output matrix : $\lfloor\frac{n+2p-f}{s}+1\rfloor\times\lfloor\frac{n+2p-f}{s}+1\rfloor$
  

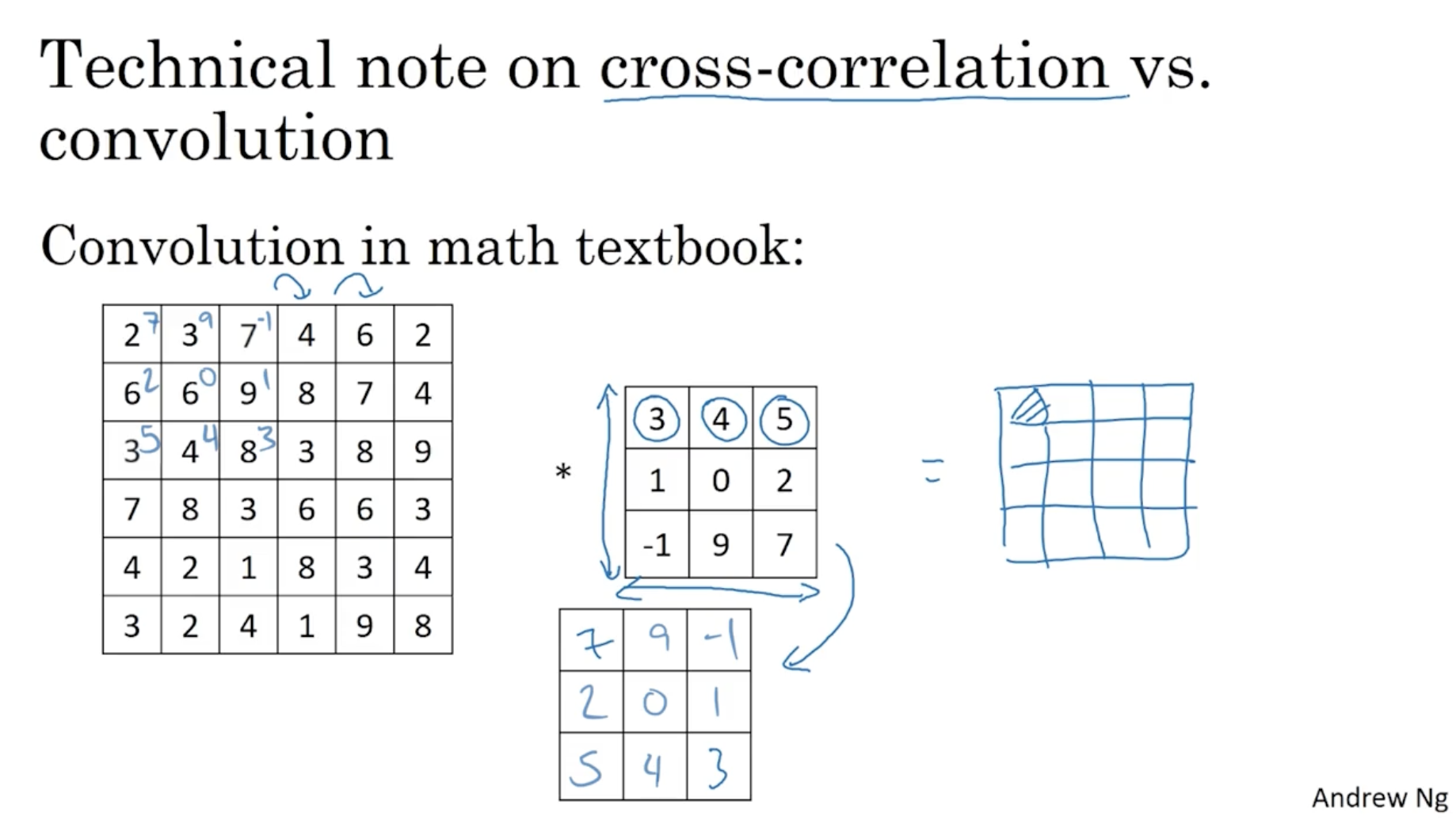
아래는 참고용으로, 일반적인 수학 교과서에서의 convolution은 아래와 같이 상하좌우가 반전된 필터로 convolution을 적용한다는 내용이다. (하지만 딥러닝에서는 그렇게 중요한 고려 요소가 아니다. 그냥 이전처럼 진행하면 된다.)

---

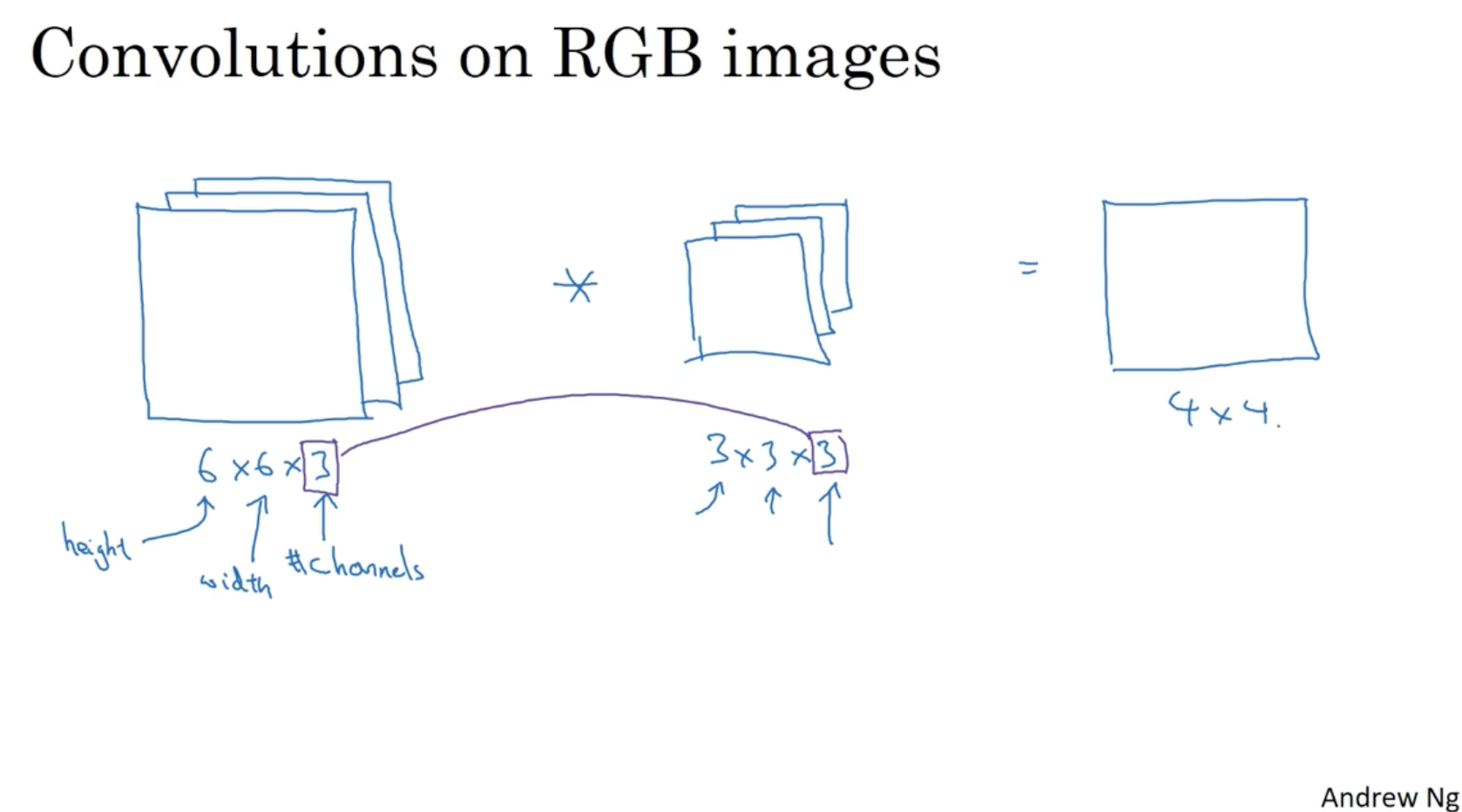
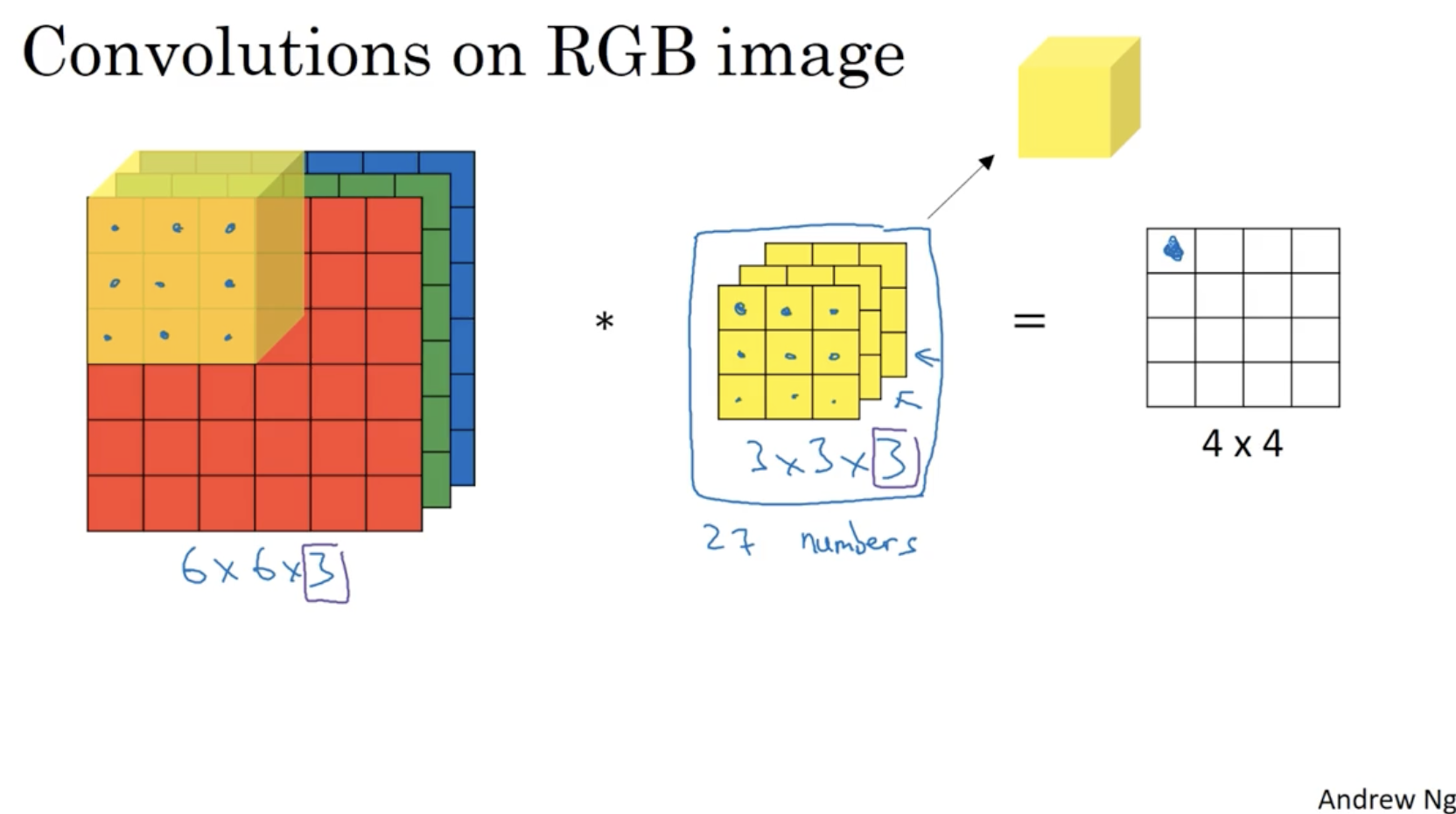
이전까지는 gray scale 이미지에 대한 convolution을 알아보았다. 그렇다면 RGB 이미지에는 어떻게 convolution을 적용할 수 있을까? 아래를 보자.

• 비교적 방법은 간단하다. 여러 개의 채널(RGB)에 대한 각각의 filter를 적용하면 된다.
• 그리고 각 convolution 값을 연산하여 하나로 묶어주면 된다.
• 아래처럼 $6(height) \times 6(width) \times 3(\# channels)$ 입력 이미지에 대해서 convolution 연산을 해야할 경우, filter는 $3\times 3 \times 3$ 으로 만들어준다.
• 그리고 연산을 진행하여 $n+2p-f+1=6+0-3+1=4$, $4 \times 4$ 크기의 output matrix를 구할 수 있다.
  

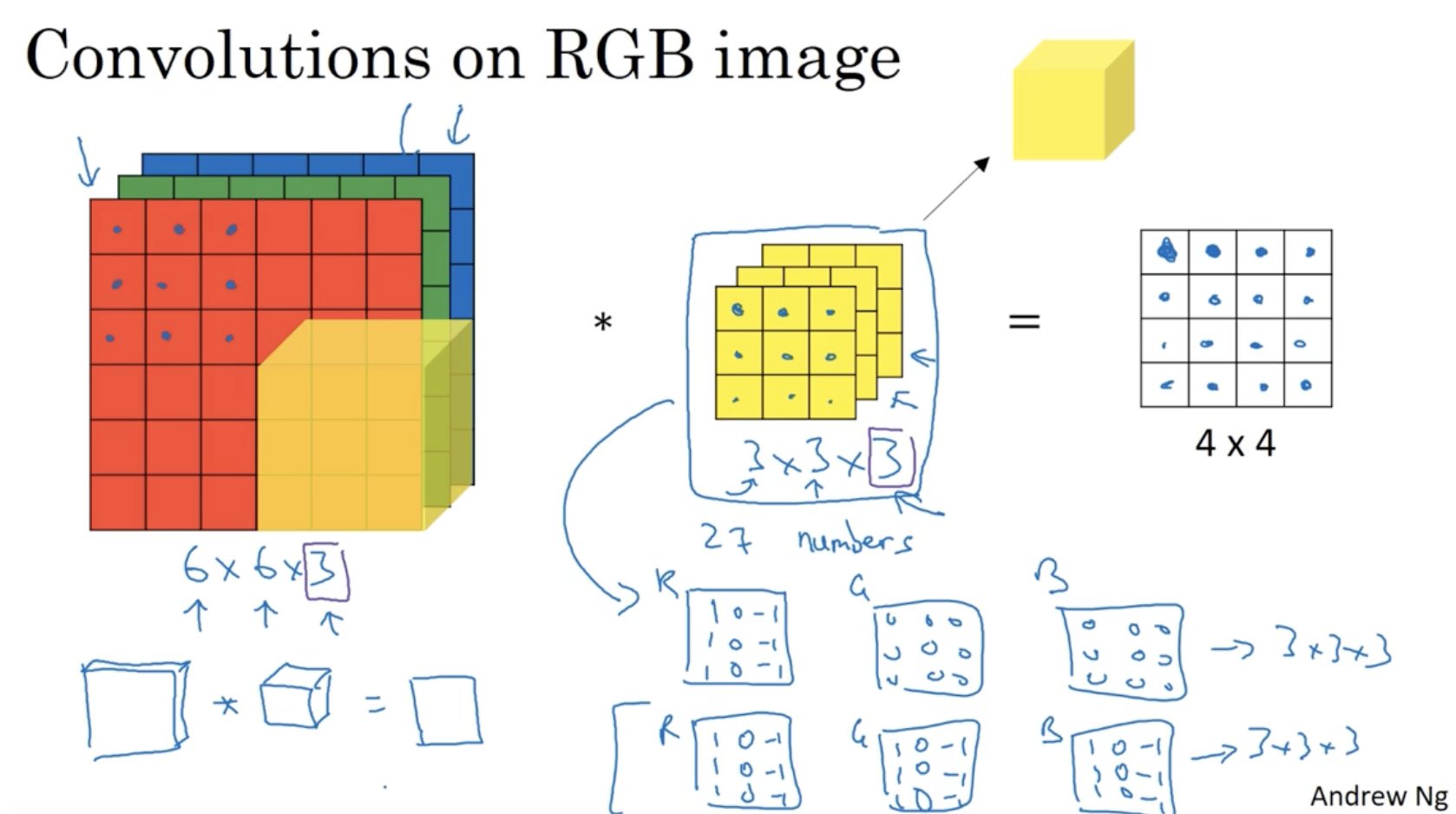
아래는 좀더 직관적인 이미지로 RGB 이미지에 대한 convolution을 적용한 예시를 보여준다.

• 만약 위에서 filter가 $R:\begin{bmatrix}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\\end{bmatrix},G:\begin{bmatrix}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\\end{bmatrix},B:\begin{bmatrix}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\\end{bmatrix}$ 처럼 적용된다면 이를 통해 나온 output matrix는 Red color의 (vertical) edge만을 나타낼 것이다.
• 반면에 $R:\begin{bmatrix}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\\end{bmatrix},G:\begin{bmatrix}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\\end{bmatrix},B:\begin{bmatrix}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \\\end{bmatrix}$ 처럼 적용된다면 output matrix는 모든 color의 (vertical) edge detection을 의미할 것이다.

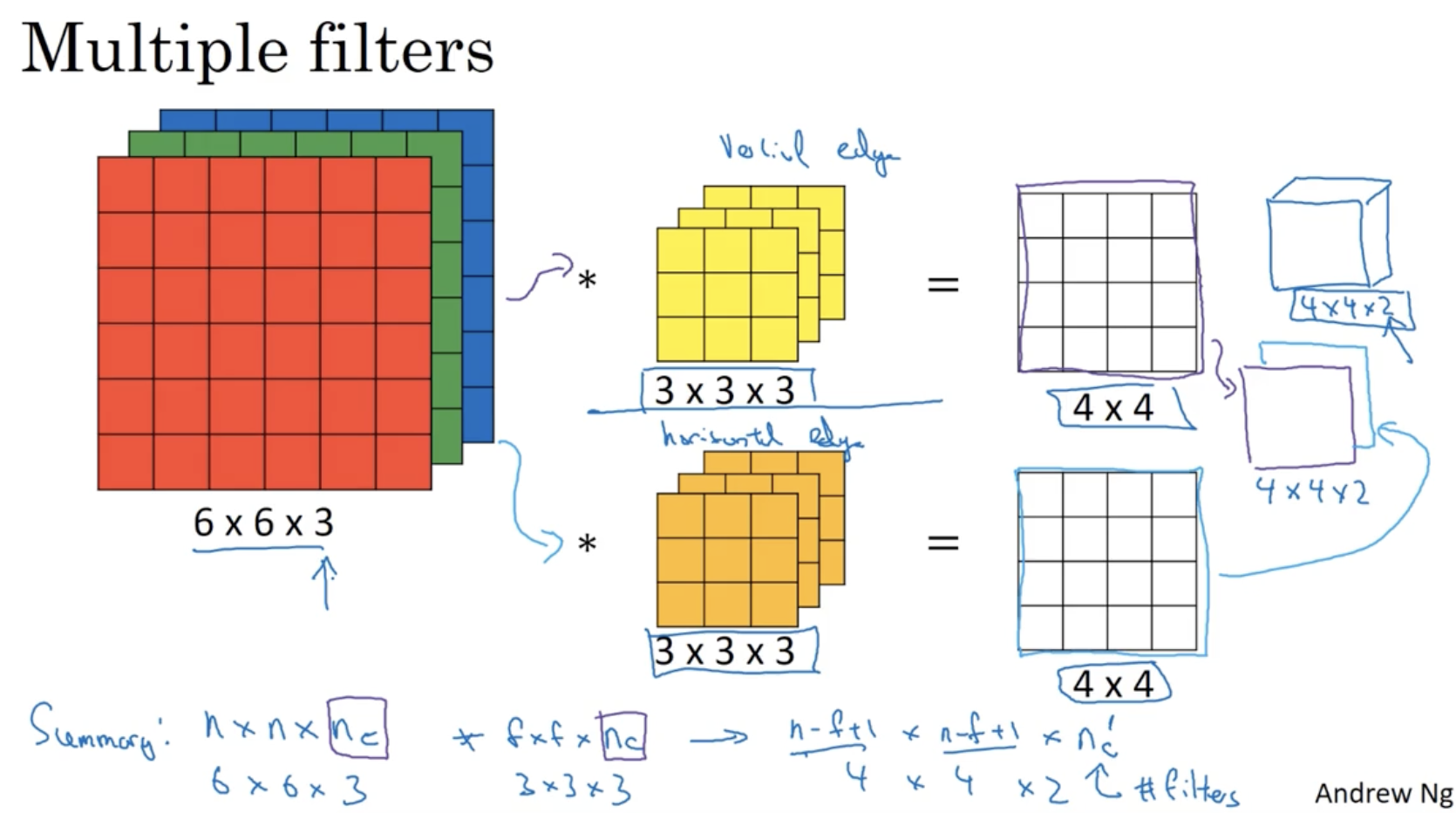
또한, vertical edge와 horizontal edge detection을 합칠 수도 있다. 아래 예시를 보자.

• RGB 이미지에 대한 필터는 크게 두 종류로 나뉜다. (vertical and horizontal)
• 다음으로 필터는 RGB에 대해서 3개의 channel을 갖는다.
• 그리고 vertical과 horizontal edge detection으로 나온 2개의 $4\times 4$ output matrix를 결합하여 $4\times 4\times 2$ 크기의 행렬로 만들어 준다. 이 최종 행렬이 vertical and horizontal edge detection 정보를 갖는 행렬이 된다.
  

---

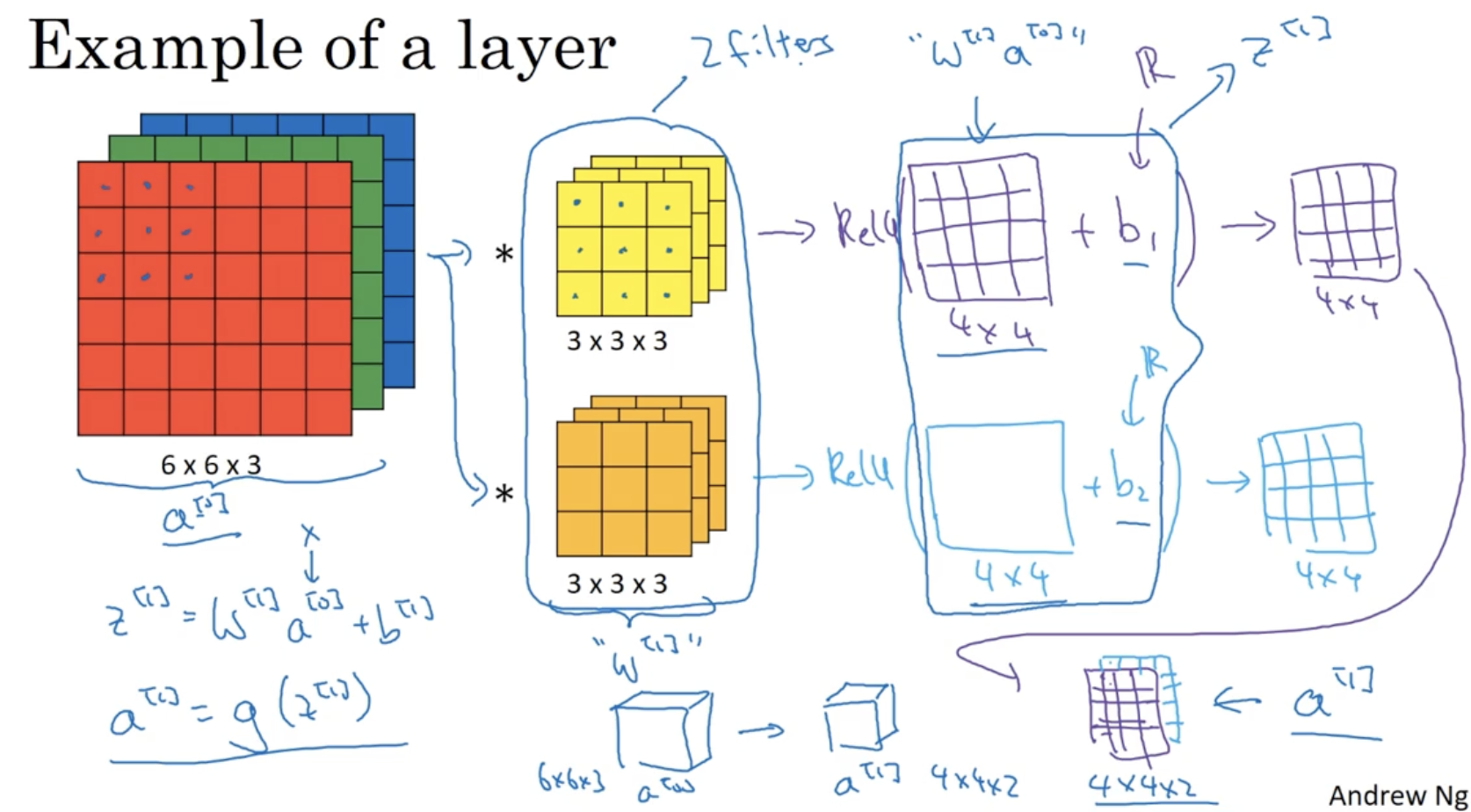
이제 convolution을 neural networks 에 적용해보자. (single layer로 해보자.)

• 아래와 같이 6 x 6 x 3 입력 데이터를 2개의 3 x 3 x 3 필터로 convolution을 한다고 해보자.
• 먼저 각 filter의 convolution 연산을 통해 2개의 4 x 4 output matrix를 구한다.
• 각 output matrix에 각각의 bias $b_1,b_2$를 더하여 준다.
• 그리고 각 output matrix에 ReLU와 같은 activation function을 적용한다.
• 그러면 activation function이 적용된 2개의 matrix가 나올 것이다.
• 이를 neural net.에 적용하면, $z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$ 에서 $W^{[1]}$은 필터를 의미하고 (정확히는 3x3x3개의 weights 요소들의 행렬을 의미하고), $b^{[1]}$은 output matrix에 broadcasting이 적용되는 bias를 의미한다.
• 그 다음 마찬가지로 activation function이 broadcasting 방식으로 적용될 것이고,
• activation function이 적용되어 나온 결과가 $a^{[1]}$이 될 것이다.
  

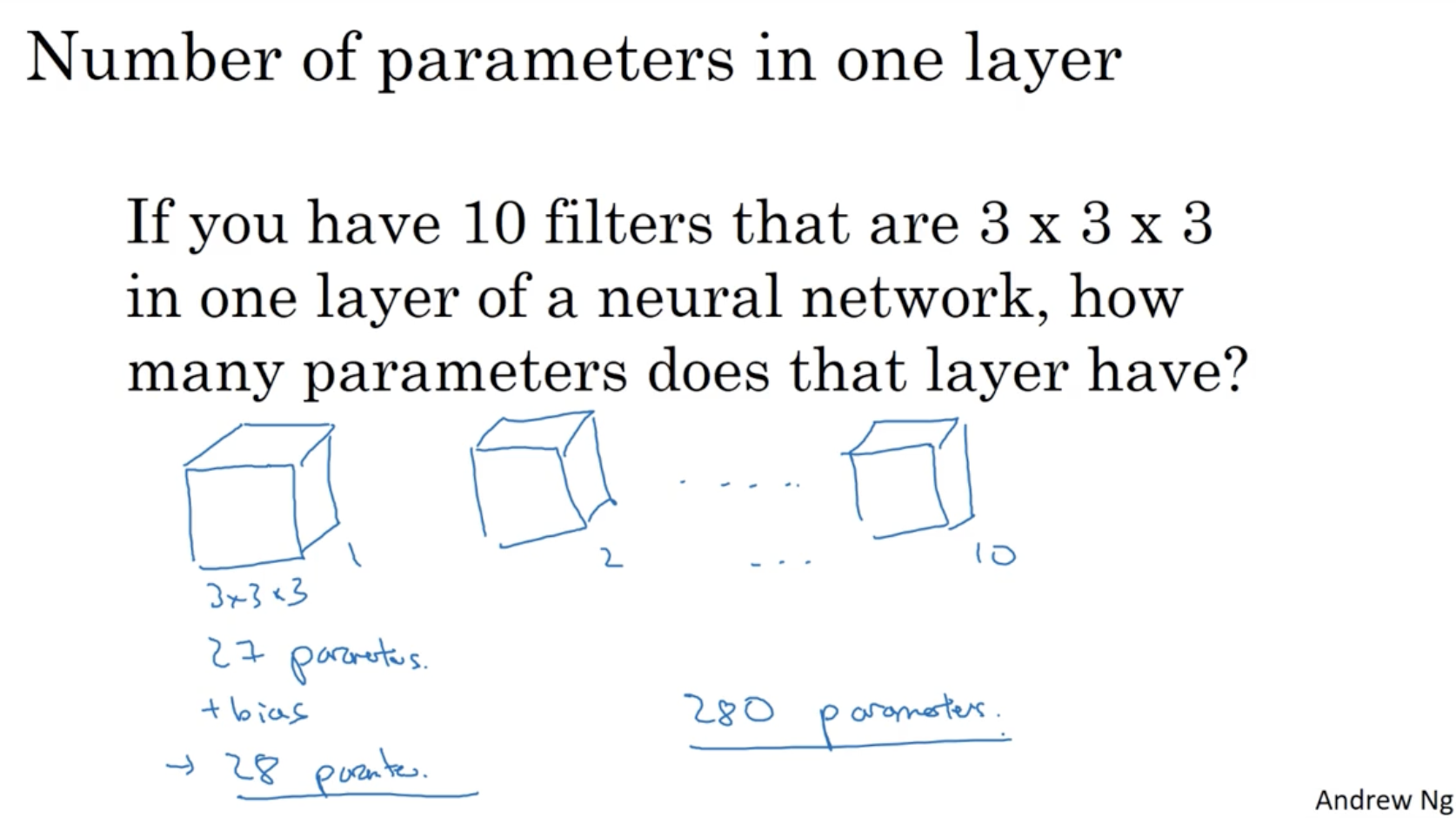
예를 들어, 10개의 3 x 3 x 3 filter를 갖는 레이어라고 가정해보자. 이 경우 필요한 파라미터는 총 몇 개일까?

• 우선 3 x 3 x 3 개의 weights 들이 있다. 즉 27개.
• 그리고 여기에 bias b를 더해줘야 하므로 27 + 1 이 된다. 28개.
• 그리고 총 10개의 filter가 존재하므로 10을 곱해준다. 280개.
• 따라서 이 경우 필요한 파라미터의 수는 총 280개 뿐이다.
• 이 경우 아무리 입력 데이터(이미지)의 차원이 크더라도 필요한 파라미터 수는 280개의 불과하다.
• 따라서 이미지 데이터에 대한 기존의 DNN 방식의 수많은 파라미터 차원과 달리, CNN 방식으로 진행할 경우 필요한 파라미터 수가 매우 적어진다는 장점이 있다.
  

CNN의 notation과 각각의 차원을 요약 정리하면 다음과 같다.

• $l$번째 convolution layer 가정.
• $f^{[l]}$ : $l$번째 convolution layer에서의 filter size.
• $p^{[l]}$ : $l$번째 convolution layer에서의 padding size.
• $s^{[l]}$ : $l$번째 convolution layer에서의 stride size.
• $n^{[l]}_c$ : $l$번째 convolution layer에서의 number of filters.
• Input : $n_H^{[l-1]} \times n_W^{[l-1]} \times n^{[l-1]}_c$
• Output : $n_H^{[l]} \times n_W^{[l]} \times n^{[l]}_c$
• $n_{output}=\frac{n+2p-f}{s}+1$
  • $n_H^{[l]}=\frac{n^{[l-1]}_H+2p^{[l]}-f^{[l]}}{s^{[l]}}+1$
  • $n_W^{[l]}=\frac{n^{[l-1]}_W+2p^{[l]}-f^{[l]}}{s^{[l]}}+1$
• $l$번째 filter 차원 : $(f^{[l]}\times f^{[l]}\times n_c^{[l-1]})$
• $l$번째 activations $a^{[l]}$ 차원 : $(n_H^{[l]} \times n_W^{[l]} \times n^{[l]}_c)$
• $l$번째 weights 차원 : $(f^{[l]}\times f^{[l]}\times n_c^{[l-1]} \times n_c^{[l]})$
• $l$번째 bias 차원 : $n_c^{[l]}$
• m 개의 데이터셋에 대한 activation matrix $A^{[l]}:(m \times n_H^{[l]} \times n_W^{[l]} \times n^{[l]}_c)$
  

---

다음은 Convolution layer가 적용된 ConvNet.에 대한 예시이다.

• 보다시피 39 x 39 x 3 입력 데이터로 시작하여 여러 번의 conv layer를 거쳐 7 x 7 x 40 출력 데이터로 마무리된다.
• 그리고 7 x 7 x 40을 벡터화하면 1960개의 원소를 갖는 $(1960, 1)$ 크기의 $\hat y$를 얻을 수 있다.
• 그리고 여기에 logistic regression이나 softmax 함수를 적용하여 classification을 할 수도 있다.
• 그리고 보통 layer가 길어질수록 입력 이미지의 크기는 줄어들고(39->7) 채널의 크기는 증가한다(3->40).
  

일반적으로 CNN의 구성 layer는 다음과 같다.

• Convolution layer (CONV)
• Pooling layer (POOL)
• Fully connected layer (FC)
• pooling layer와 fully connected layer는 바로 다음 강의에서 다룬다.
  

---

다음으로 pooling 에 대해서 알아본다.

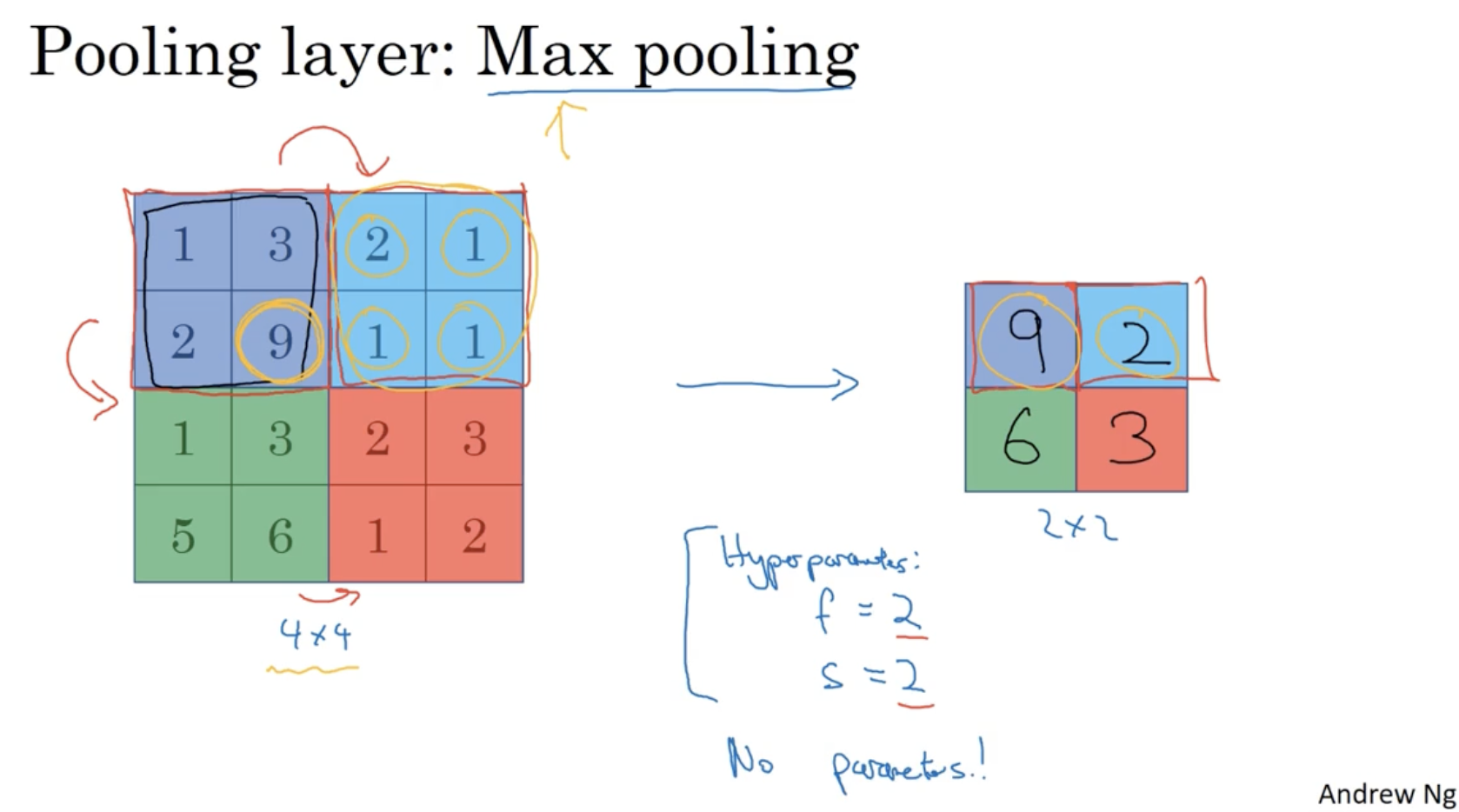
• 아래는 max pooling에 대한 예시이다.
• 아래와 같이 2 x 2 크기의 region에 대해서 stride를 2씩 옮기며 각각의 최대값을 추출한 행렬을 얻는다.
• 출력된 행렬을 보고, 9에 해당하는 쪽에 특정 feature(ex. 고양이 눈)가 존재하고 2에 해당하는 쪽에는 특정 feature(고양이 눈)가 존재하지 않는다고 추측할 수 있다.
• 그리고 아까 convolution의 filter에 적용하는 것처럼 pooling region도 $f$, $s$를 통해서 결정하며, filter와 달리 pooling에서는 lerning 과정이 존재하지 않는다.
  

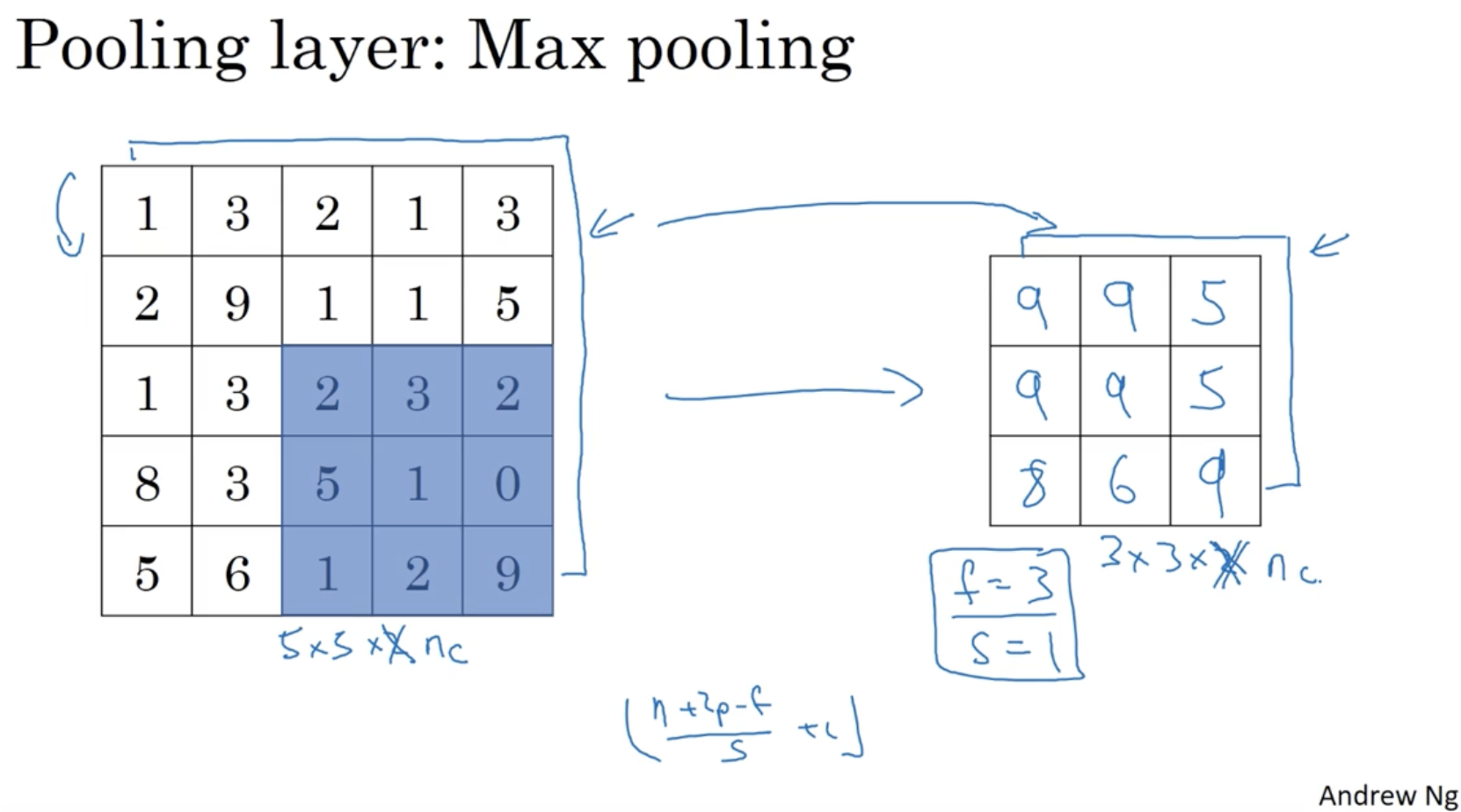
예시로 5 x 5 행렬에 (f=3, s=1) max pooling을 적용한 예시는 아래와 같다.

• 그리고 filter convolution과 마찬가지로 입력 데이터의 채널 수 $n_c$에 따라 pooling 결과의 채널 수가 결정된다. 그리고 각각의 pooling은 독립적으로 진행된다.
  

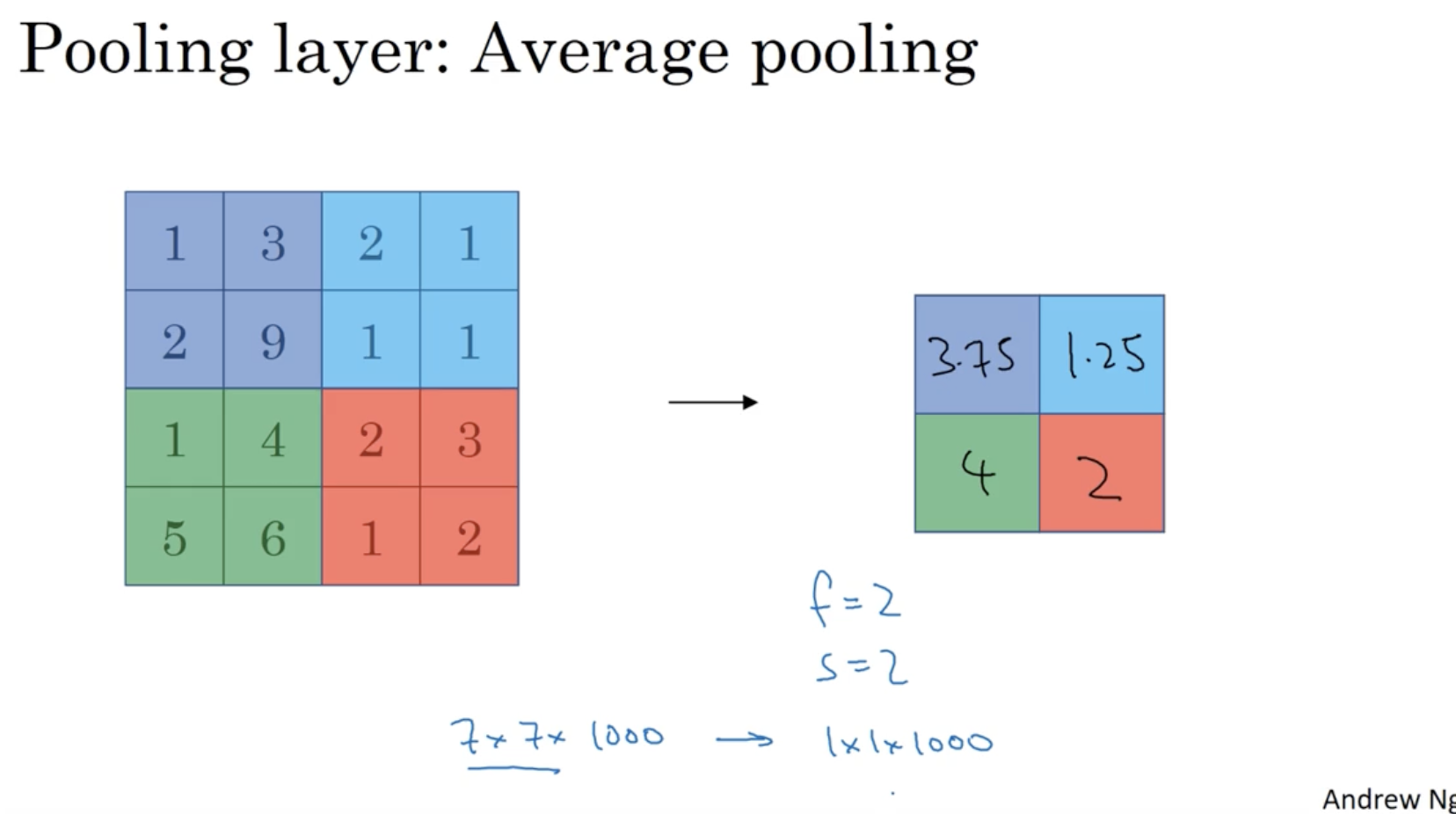
아래는 average pooling의 예시이다.

• max pooling과 달리 모든 요소의 평균값을 추출한 행렬을 얻는다.
• max pooling이든 average pooling이든 결국에는 pooling을 통해서 데이터의 차원을 줄일 수 있다.
  

pooling의 내용을 요약하면 아래와 같다.

• 하이퍼 파라미터
  • f : filter size
  • s : stride
  • max인지 혹은 avg인지.
  • 그리고 pooling에서는 learning 과정이 없다. (한번 하이퍼 파라미터를 설정하면 그 값에는 변화가 없다.)
• pooling의 output matrix의 차원은 다음과 같다.
  • input : $n_H\times n_W \times n_c$
  • output : $\lfloor \frac{n_H-f}{s}+1 \rfloor \times \lfloor \frac{n_W-f}{s}+1 \rfloor \times n_c$
    

---

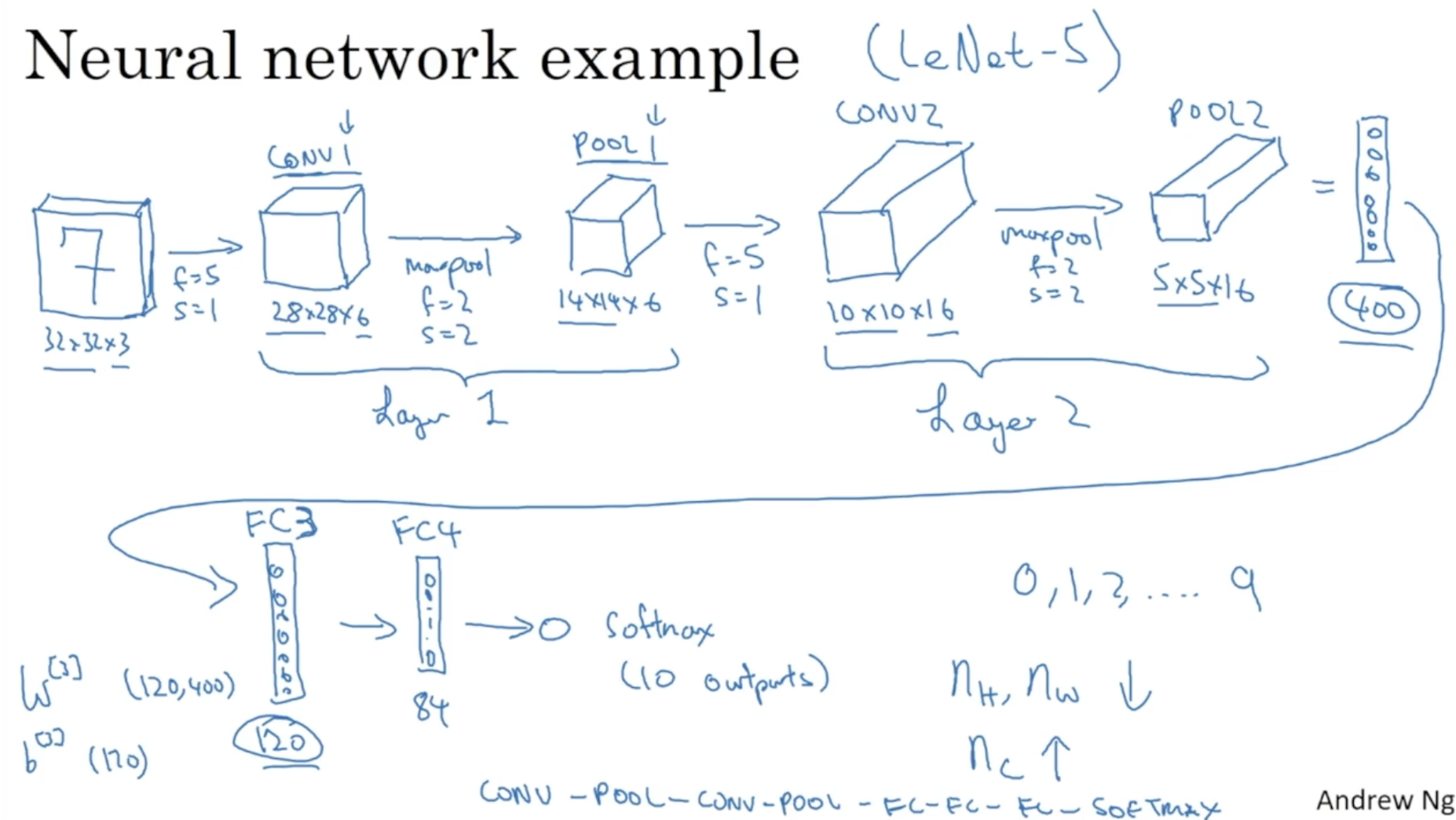
다음은 pooling과 fully conntected layer가 추가된 CNN의 구조를 나타내는 예시이다. (LeNet-5)

• 7이라고 적혀 있는 32 x 32 x 3 크기의 이미지 데이터를 입력으로 넣어서 0, 1, 2, ..., 9 중 하나의 숫자로 인식하는 모델이다.
• 보다시피 (CONV1 + POOL1) -> (CONV2 + POOL2) -> (vectorization) -> FC3 -> FC4 -> ... -> softmax 구조로 이루어져 있다.
• fully connected layer는 비교적 간단한 방식으로 이루어진다. 아래 예시에서 400 차원의 벡터에 대해서 $W : (120, 400)$ 를 적용하여 120 차원의 벡터로 만들 수 있다. 또 이 120 차원의 벡터에 대해서 $W : (84, 120)$을 적용하여 84 차원의 벡터로 만들 수 있다.
• 그리고 이 벡터에 softmax를 적용하여 0~9 중 하나의 숫자로 예측할 수 있다.
• 보다시피 모델의 layer가 깊어질수록 이미지 크기($n_H,n_W$)는 줄어들고, 채널 크기($n_c$)는 증가한다.
  

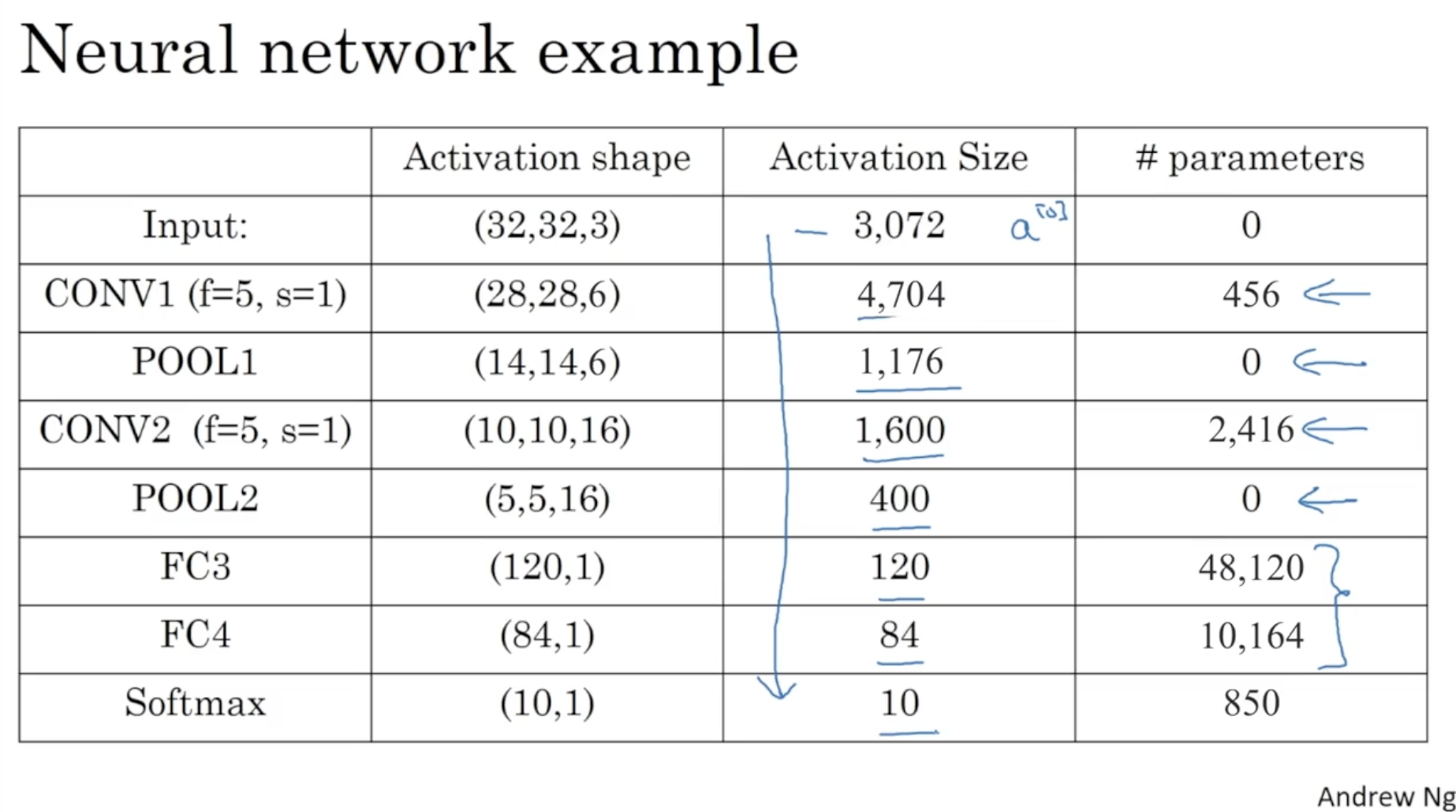
위 과정을 표로 정리하면 아래와 같다. layer가 깊어질수록 activation size가 점점 줄어드는 것을 확인할 수 있다.

---

그렇다면 왜 convolution neural net. 이 효과적인지를 알아보자.

• 아래와 같이 32 x 32 x 3 데이터를 28 x 28 x 6 데이터로 만든다고 해보자.
• 만약 일반적인 DNN이라면 학습을 위해 3072 x 4704 개의 weights가 필요할 것이다.
• 하지만 CNN의 경우 이를 위한 filter만 있으면 학습이 가능하다. (5 x 5 = 25개 + bias 1개) x 6 = 156. 즉, 156개의 weights 정보만 있으면 아래 과정을 학습할 수가 있다. 매우 효율적이다.
  

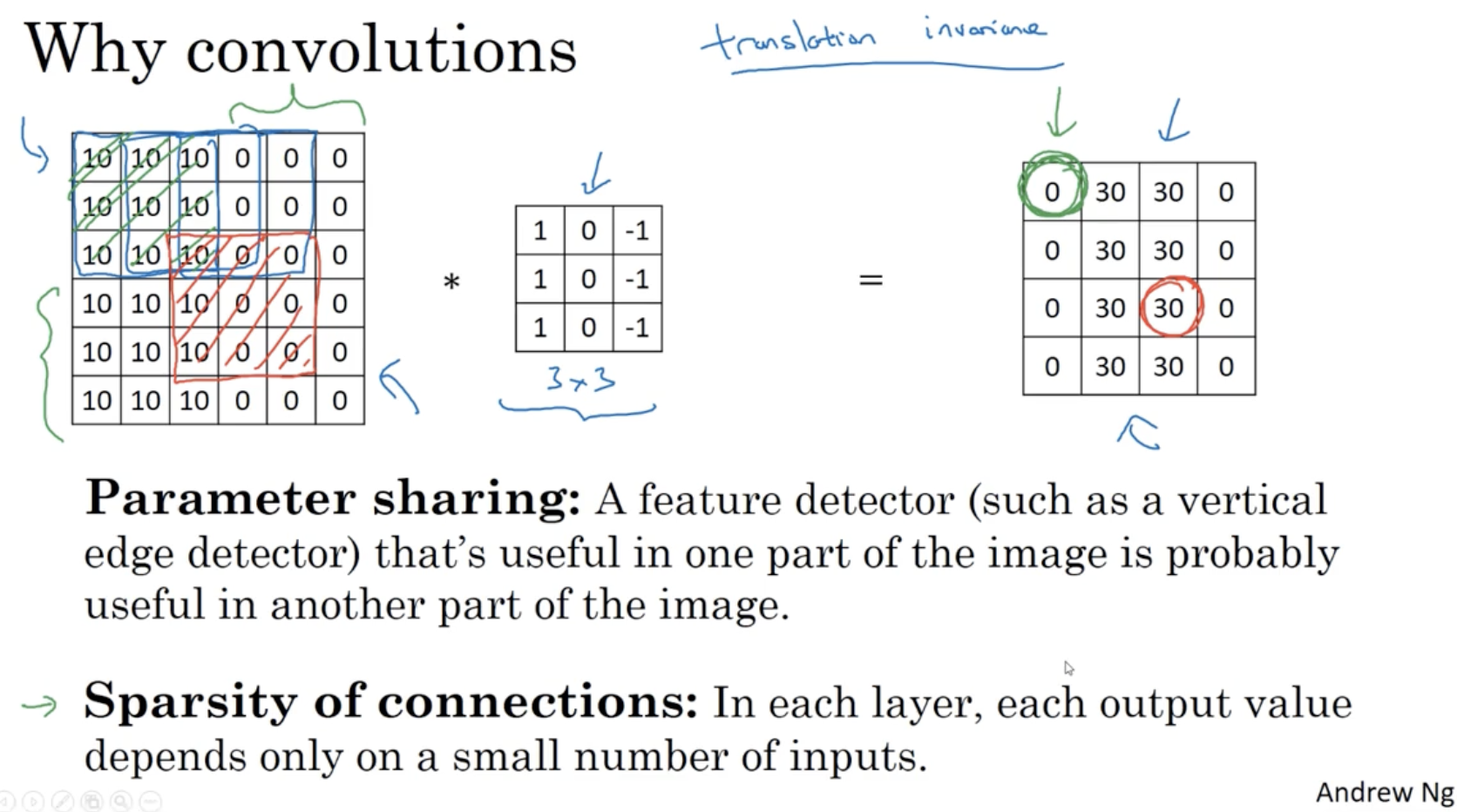
왜 이런 연산이 가능한지는 아래와 같다.

• 하나의 채널의 데이터는 동일한 filter를 공유하기 때문에 파라미터 수가 많이 필요하지 않다.
• 출력 행렬의 요소들은 전체 입력 행렬의 요소를 따지는 것이 아니라 일부 region만 따지면 되기에 파라미터 수가 많이 필요하지 않다.
  

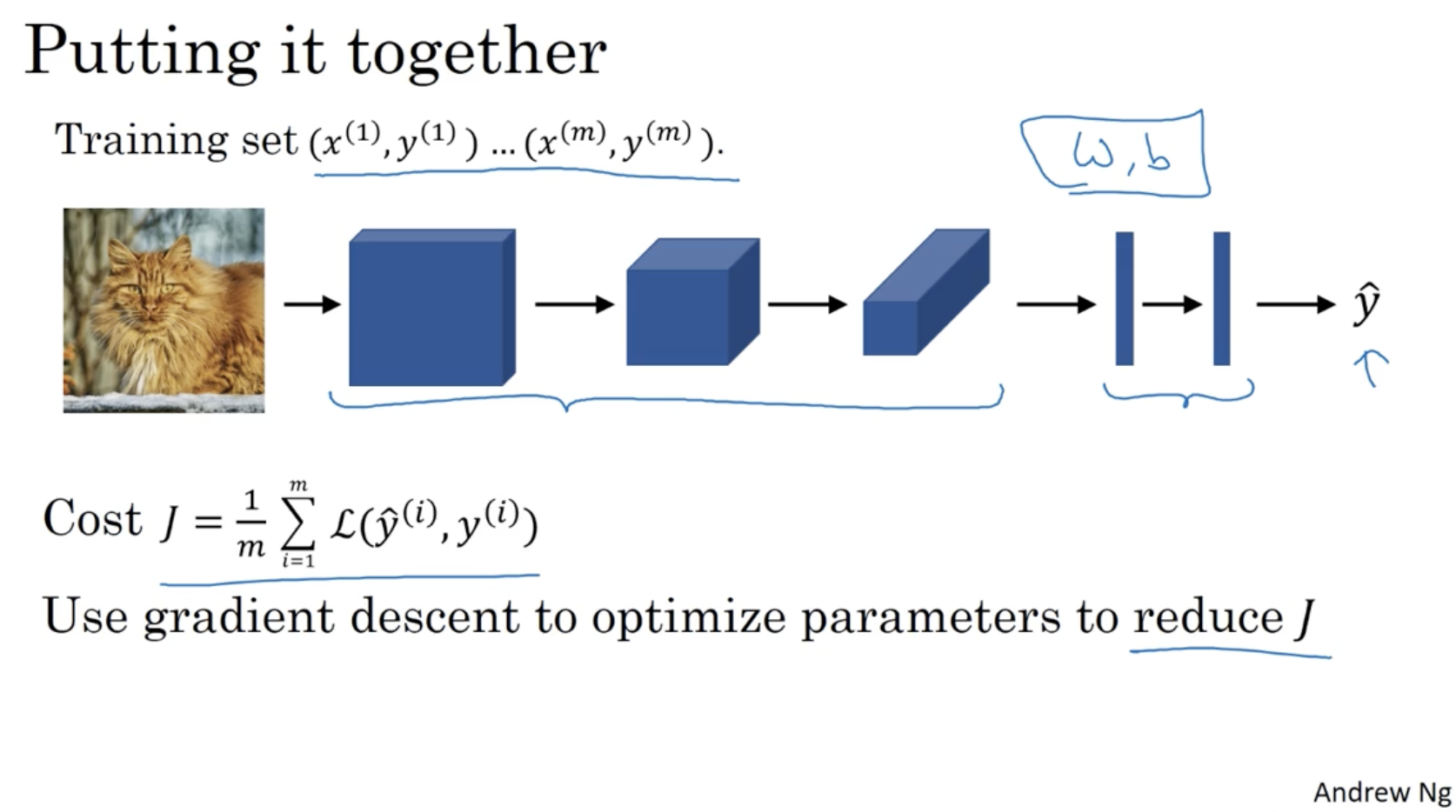
그래서 m개의 데이터셋에 대해서 CNN을 적용하면 아래와 같다.

• 이미지 데이터에 CNN(conv. + pool + fc + ...)을 적용하여 예측값 $\hat y$를 구한다.
• 그리고 cost function $J=\frac{1}{m}\sum_{i=1}^mL(\hat y^{(i)}, y^{(i)})$을 구한다.
• $J$를 줄이기 위한 최적화된 parameter를 찾기 위해 gradient descent alg.을 적용한다.