[딥러닝] Convolutional Neural Networks Week 2

출처 : https://www.coursera.org/specializations/deep-learning

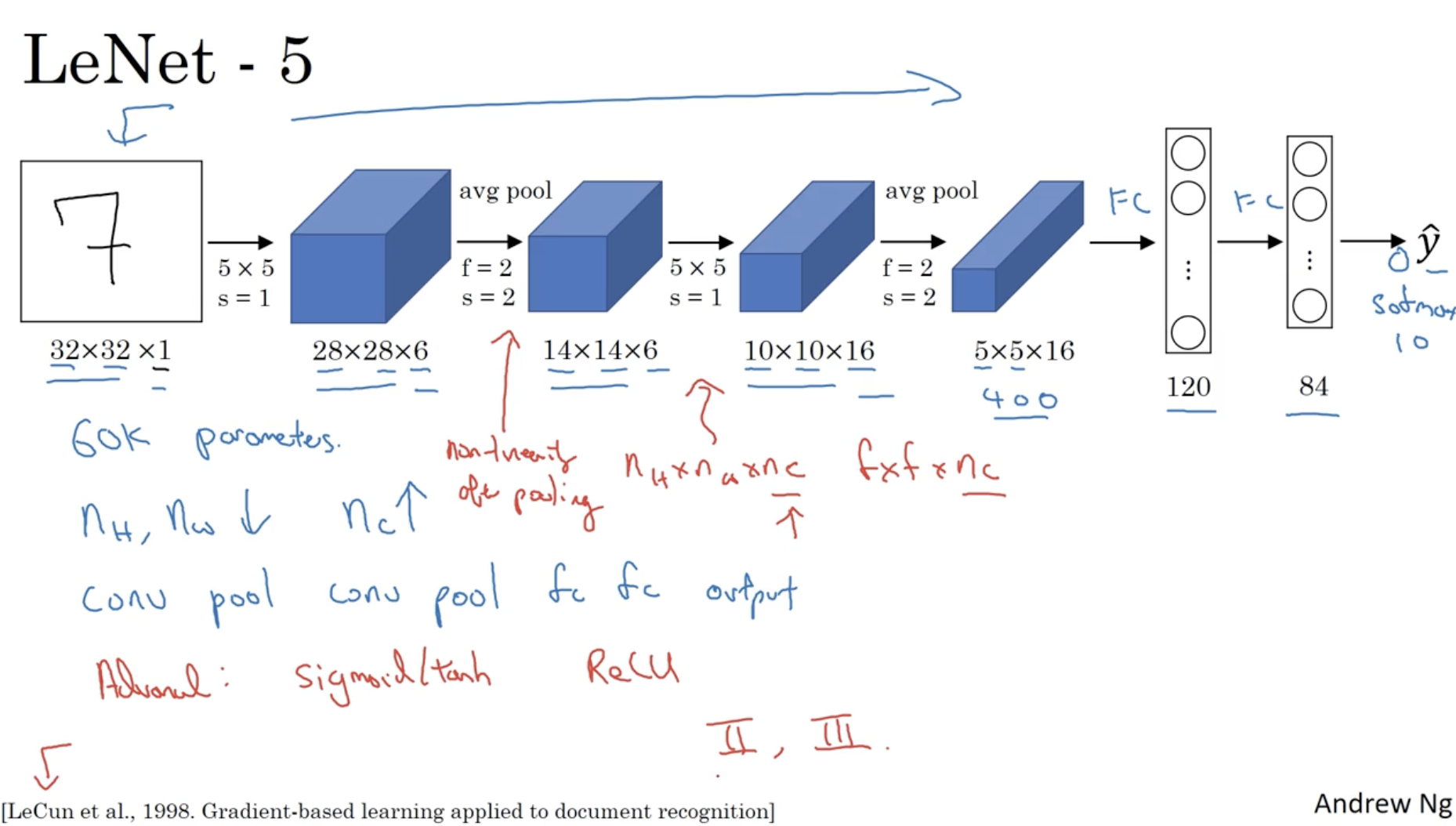
CNN의 가장 베이직한 모델인 LeNet-5의 구조는 아래와 같다.

• 약 60,000개의 학습 파라미터를 갖는다.
  

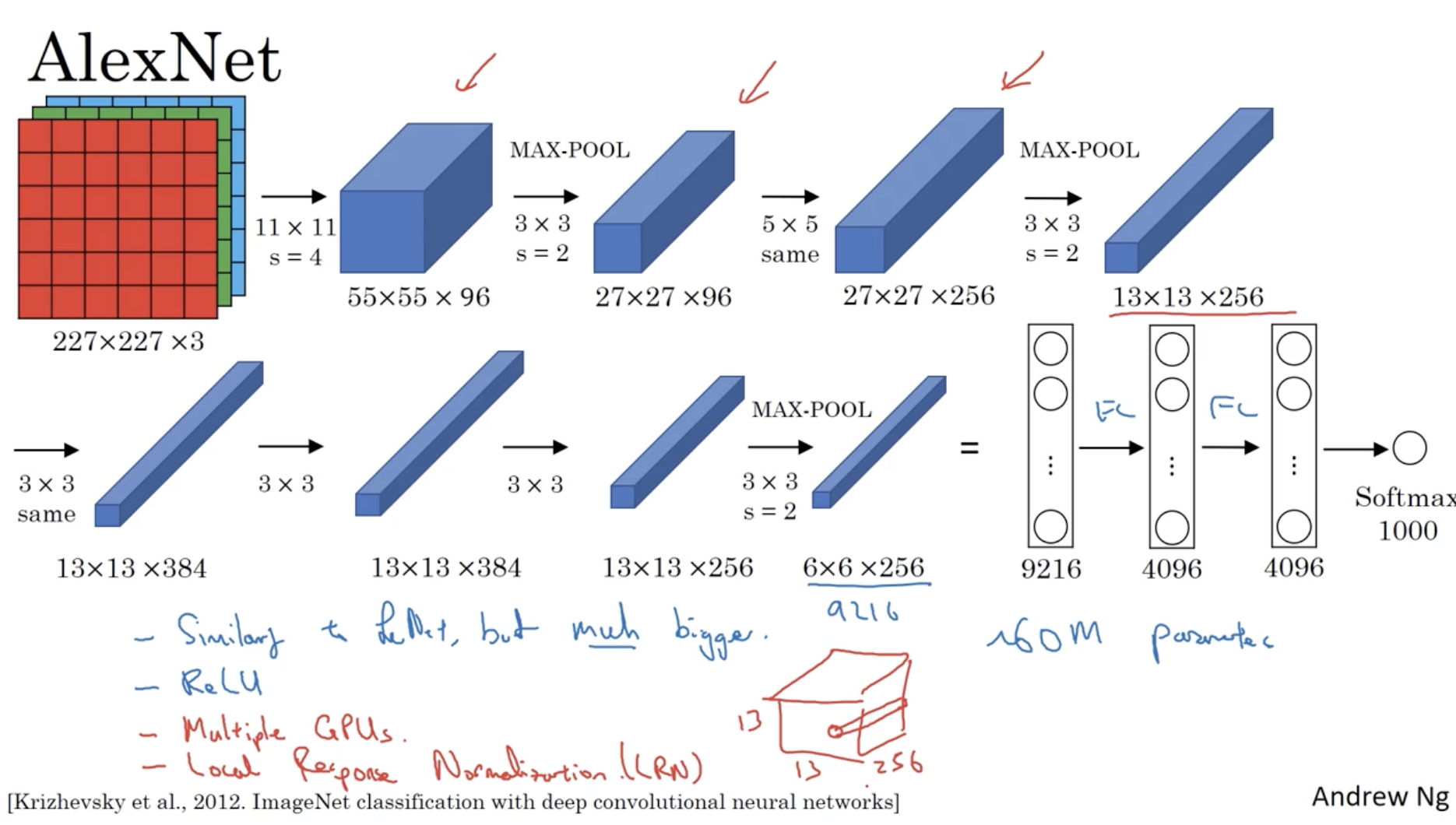
LeNet-5 다음으로 발전된 모델은 AlexNet으로 구조는 아래와 같다.

• 약 60,000,000개의 학습 파라미터를 갖는다.
  

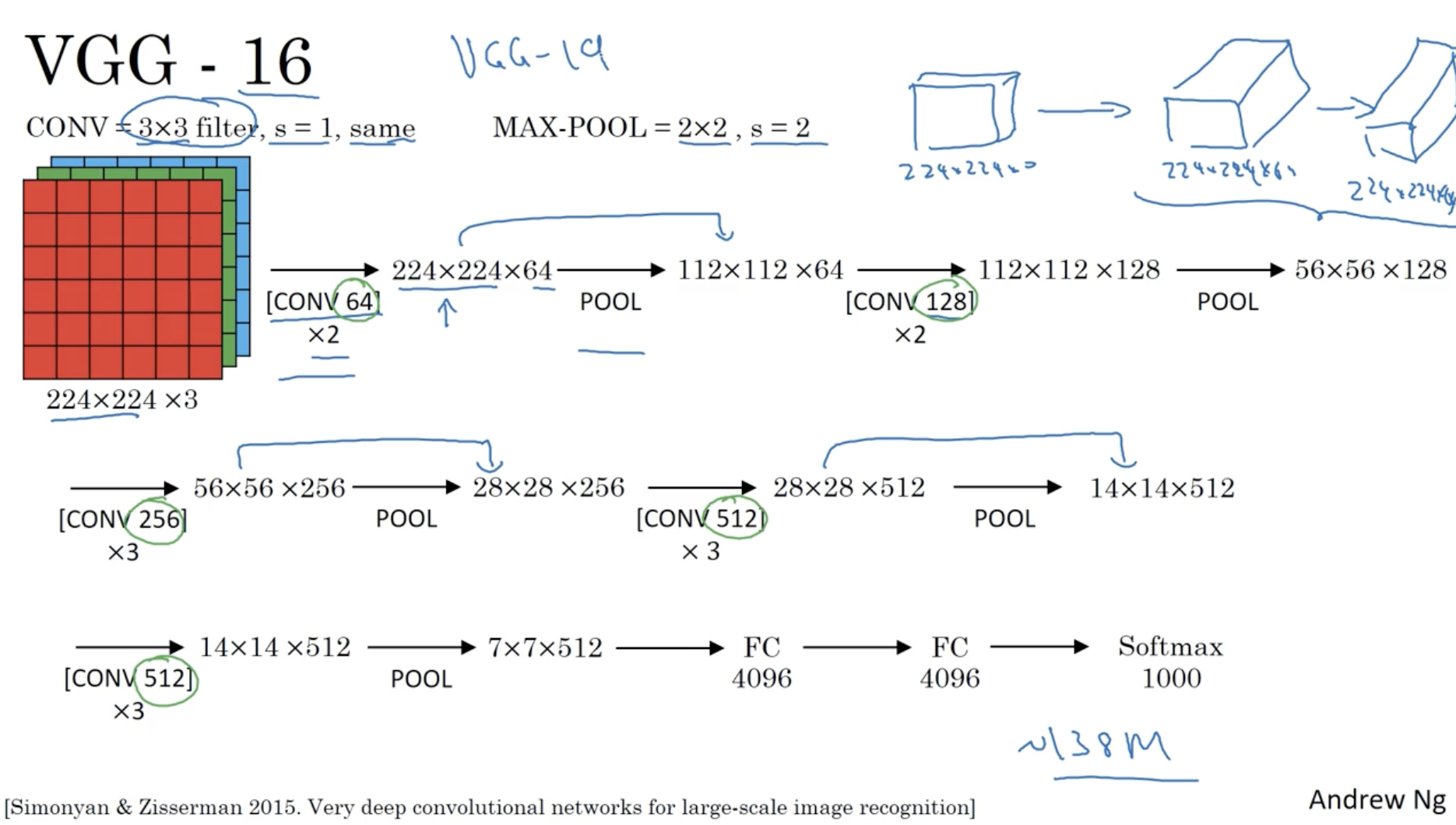
그리고 Classic한 CNN 모델 중 가장 정확도가 높은 모델 VGG-16의 구조는 아래와 같다.

• 약 138,000,000개의 학습 파라미터를 갖는다.
  

---

다음으로 ResNet에 대해서 알아본다.

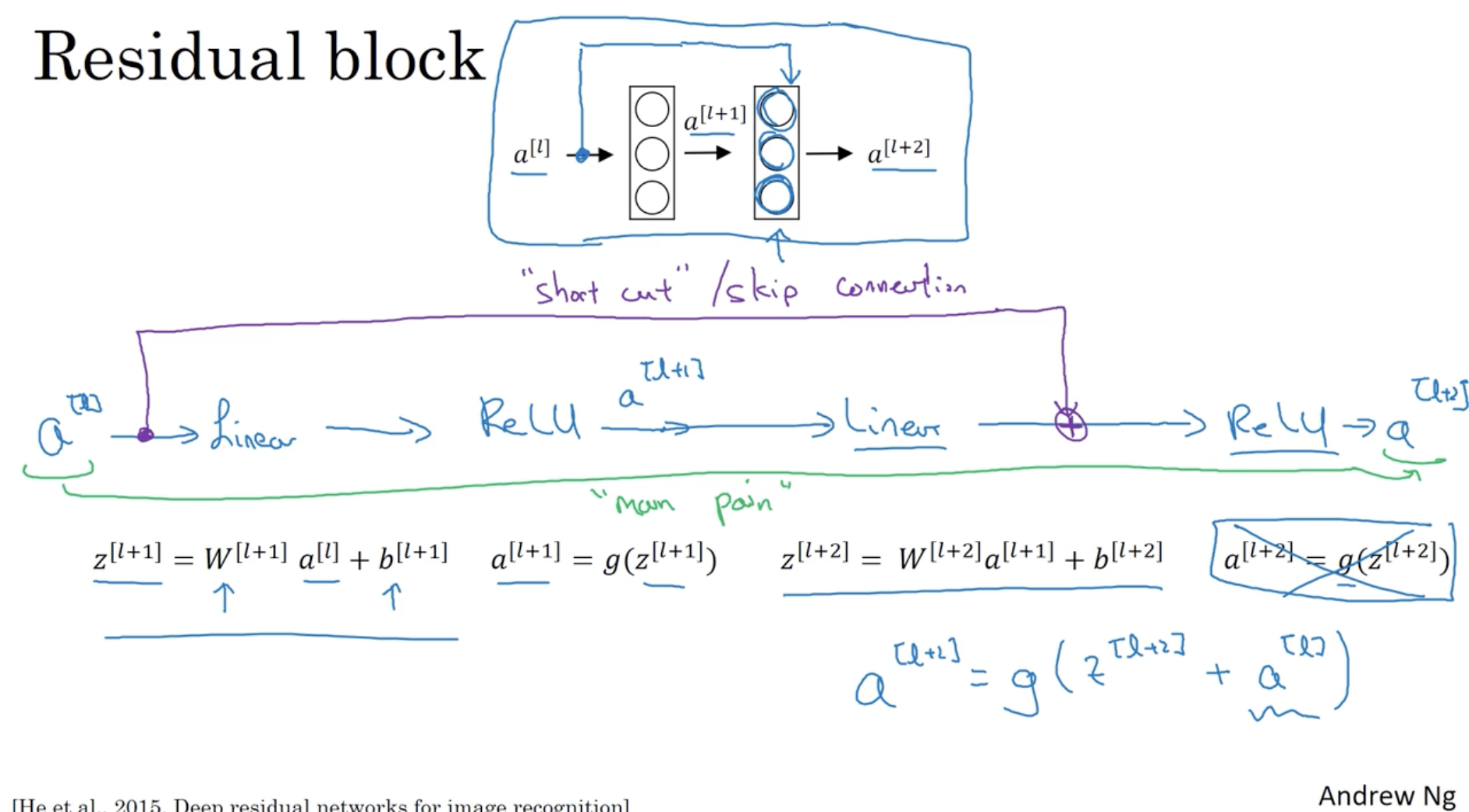
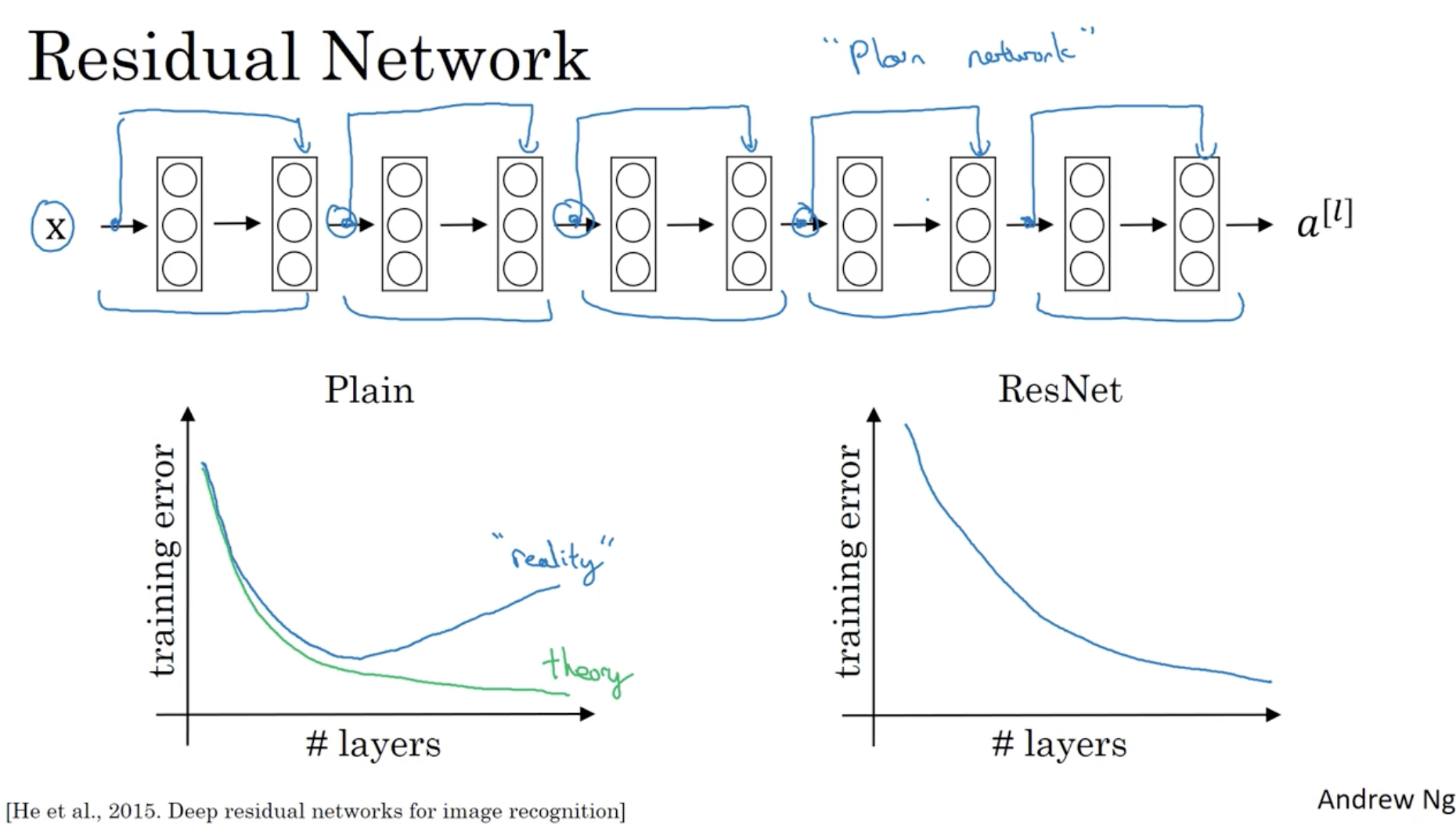
• ResNet의 주요 방법론은 아래와 같다.
• 일반적으로 neural network이 deep해질수록 gradient vanishing 등의 문제가 발생하여 모델의 구조가 커질수록 학습이 제대로 안 될 수 있다.
• 하지만 Residual block 개념을 적용하면 이전 레이어들의 값들을 반영할 수 있어 위와 같은 문제를 해결할 수 있다. (deep한 모델도 학습이 가능하다.)
• 방법은 다음과 같다. 선형의 값을 갖고 연산하는 즉, 선형성을 띄는 layer들이 있을 때, short cut (sikp connection) 을 활용하여 비선형 activation function이 적용되기 전에 이전의 값을 더해준다. ($a^{[l+2]}=g(z^{[l+2]}) \to a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$)
  

그리고 residual 개념이 적용된 모델과 ResNet을 비교했을 때, 레이어가 많아져도 ResNet은 학습 에러가 낮아진다는 것을 확인할 수 있다.

---

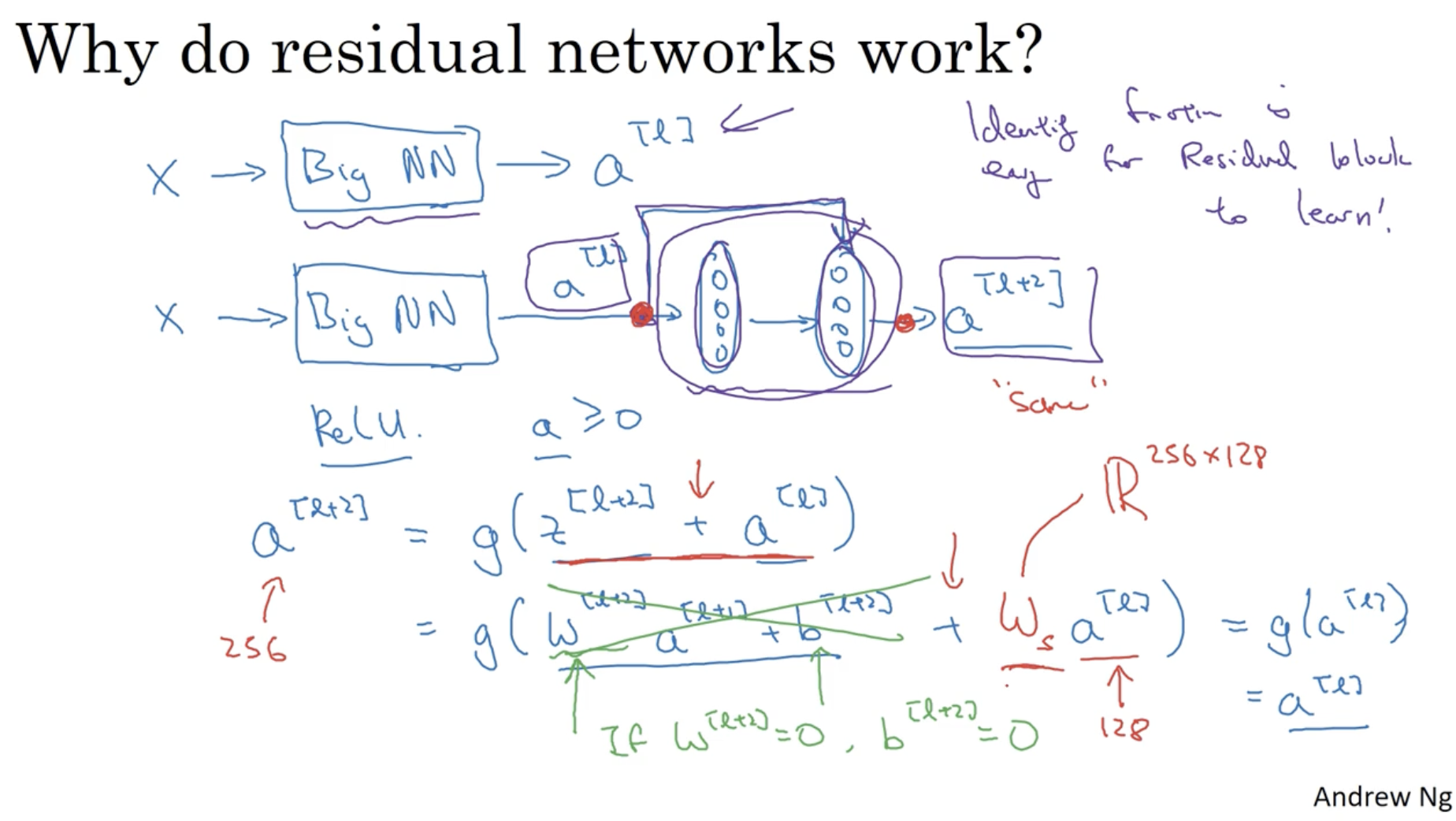
ResNet이 잘 작동하는 이유는 아래와 같다.

• 일반적인 모델과 달리 Residual Block을 적용하여 이전 값을 반영해준다.
• 예를 들어 $a^{[l+2]}=g(z^{[l+2]}+a^{[l]})=g(w^{[l+2]}a^{[l+1]}+b^{[l+2]} + a^{[l]})$ 에서 만약 regularization에 의해 $w^{[l+2]}$가 0이 나왔다고 해보자. 이 경우 short cut 에 의해서 $a^{[l+2]}=a^{[l]}$로 결과가 0이 되지 않고 값이 유지가 될 수 있다. (왜냐하면 ReLU를 적용하였기 때문에 값이 그대로 전달된다. ReLU=max(0, z))
• 따라서 모델이 깊어져도 유지가 잘 되는 것이다.
• 그리고 $g(z^{[l+2]}+a^{[l]})$ 연산에서 $z^{[l+2]}$와 $a^{[l]}$의 차원이 같다는 것을 알 수 있다. 왜냐하면 ResNet의 경우, 동일한 크기의 filter와 pooling을 적용하기 때문에 대부분의 차원이 같을 것이다.
• 만약 차원이 다르다면 $W_s$를 곱하여 차원을 맞춰주면 된다.
  

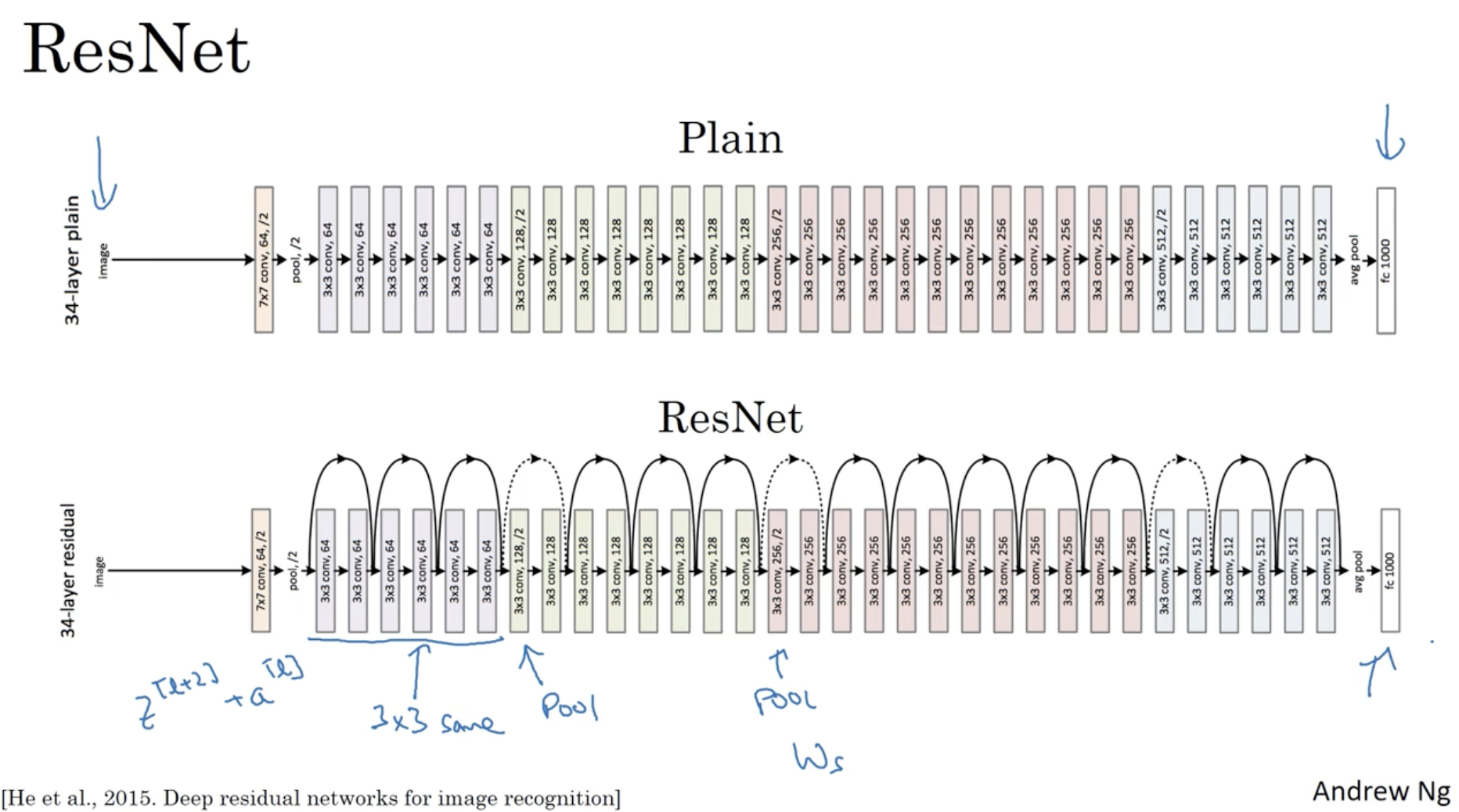
논문에서 나오는 ResNet의 구조 이미지는 아래와 같다.

---

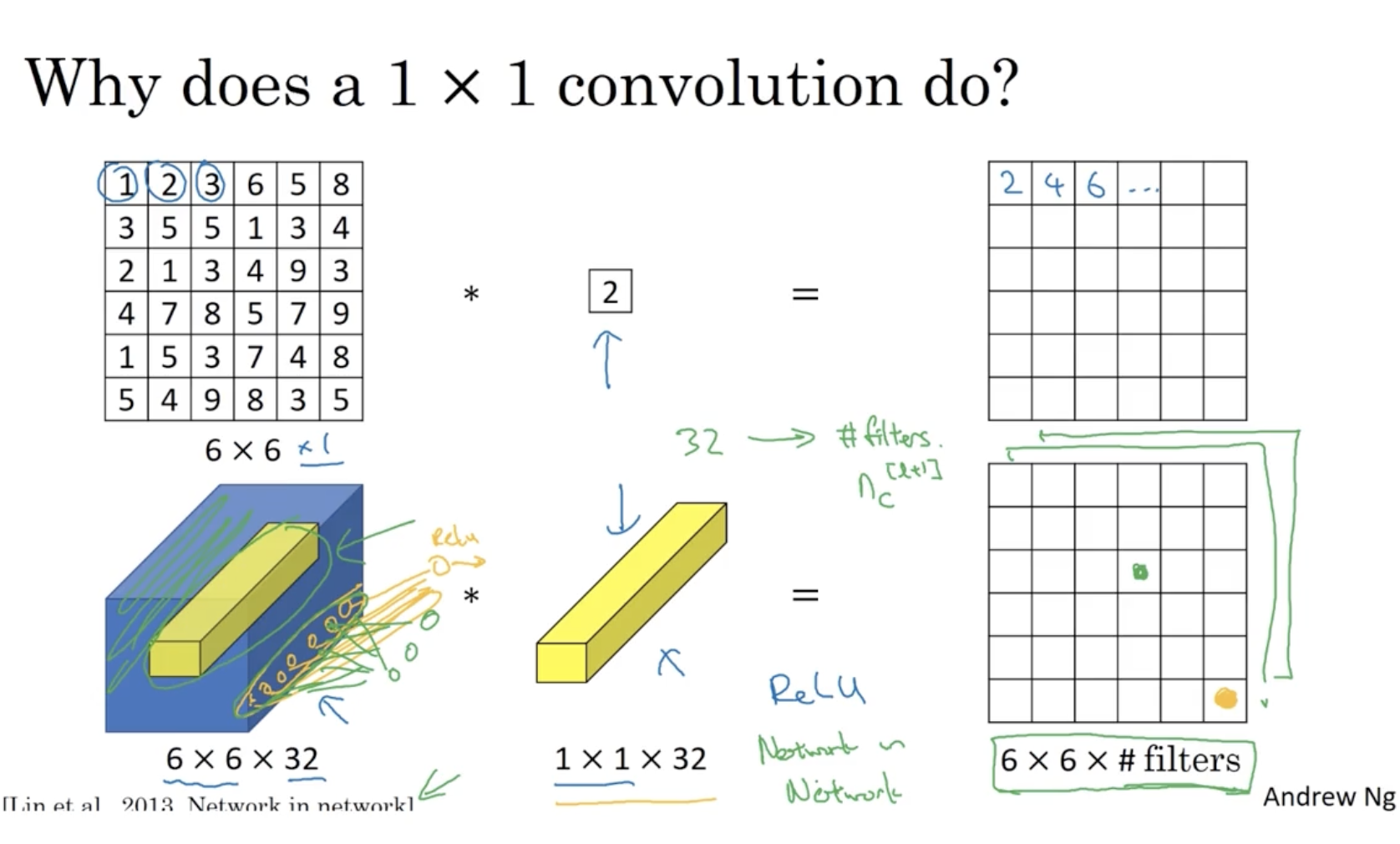
그렇다면 1 x 1 conv filter를 생각해보자. 이는 어떻게 작동하며 어떤 용도로 사용될까?

• 아래와 같이 1 x 1 conv.는 element-wise product 같은 느낌이 있다.
• 그리고 맨 아래처럼 다중 채널에 대해서 적용할 때는 각 채널의 해당하는 값들을 모두 연산하여 하나로 합친 후 ReLU와 같은 함수를 적용하여 하나의 값으로 출력한다. 예를 들어 좌측의 32개의 채널에 대한 오렌지색 데이터들을 하나로 합친 후 ReLU를 적용하여 우측과 같이 하나의 데이터로 출력한다.
• 이 원리를 Fully connected layer에 적용할 수 있다.
  

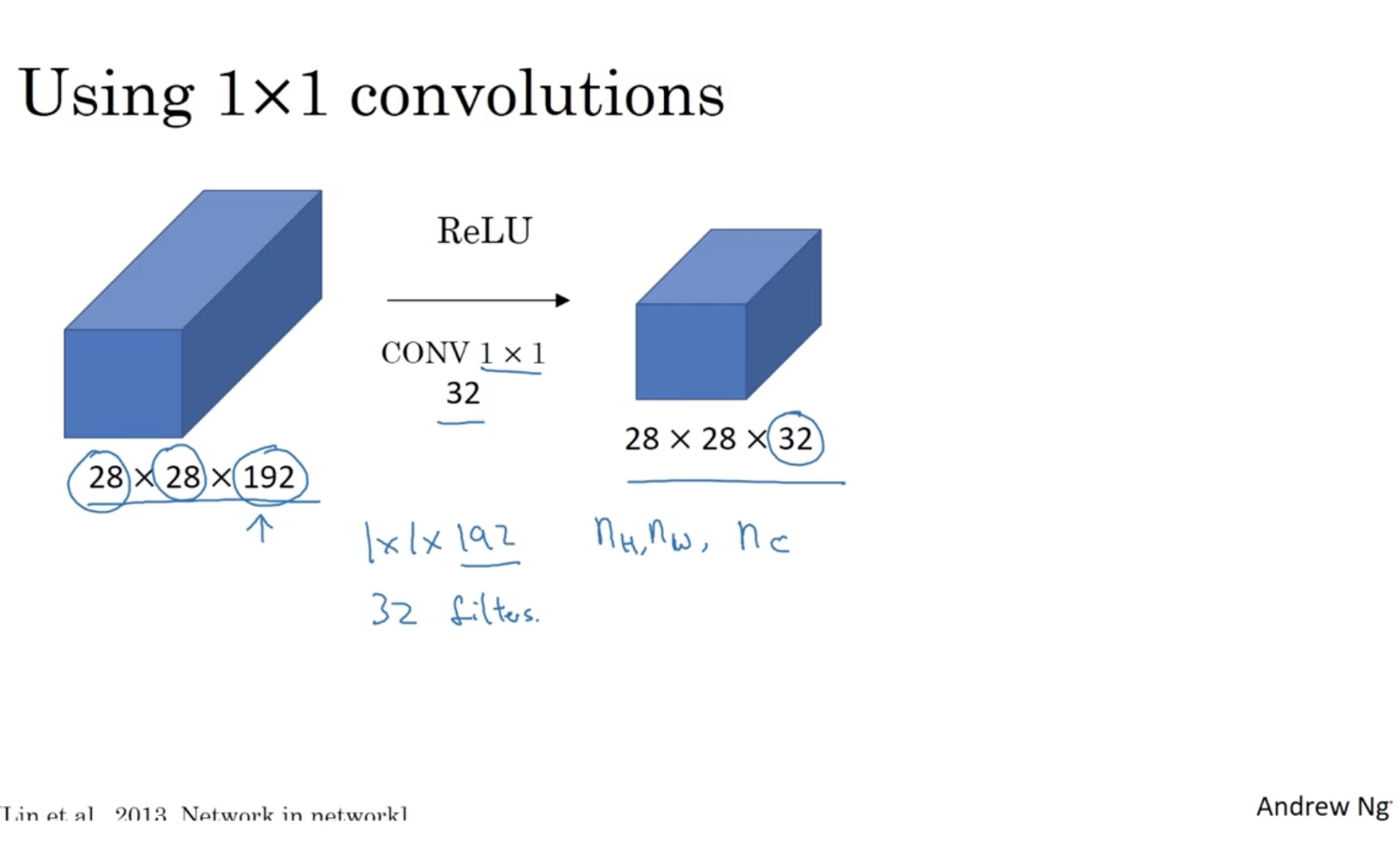
아래는 192 채널의 사이즈를 32 채널로 줄이는 예시를 보여준다.

---

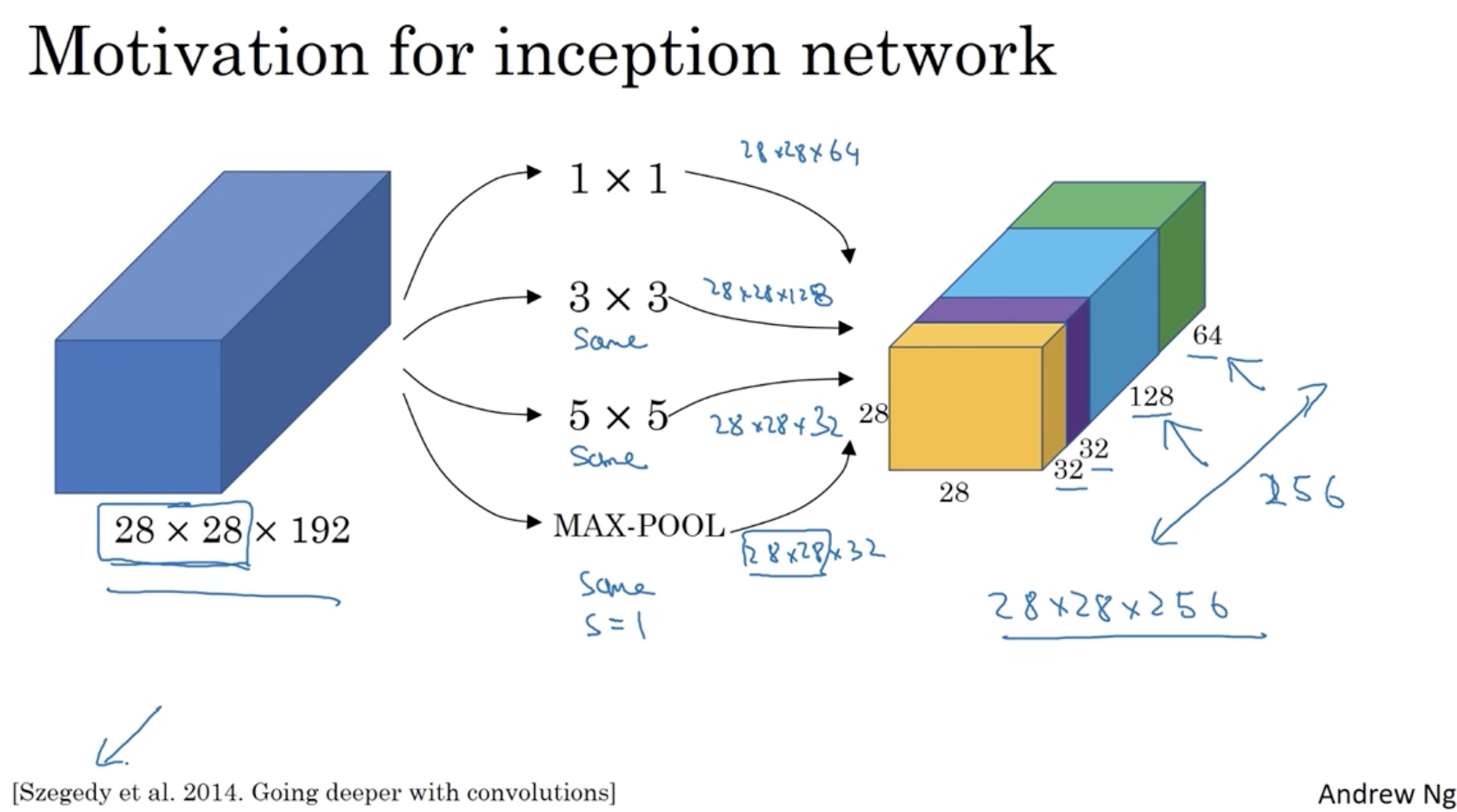
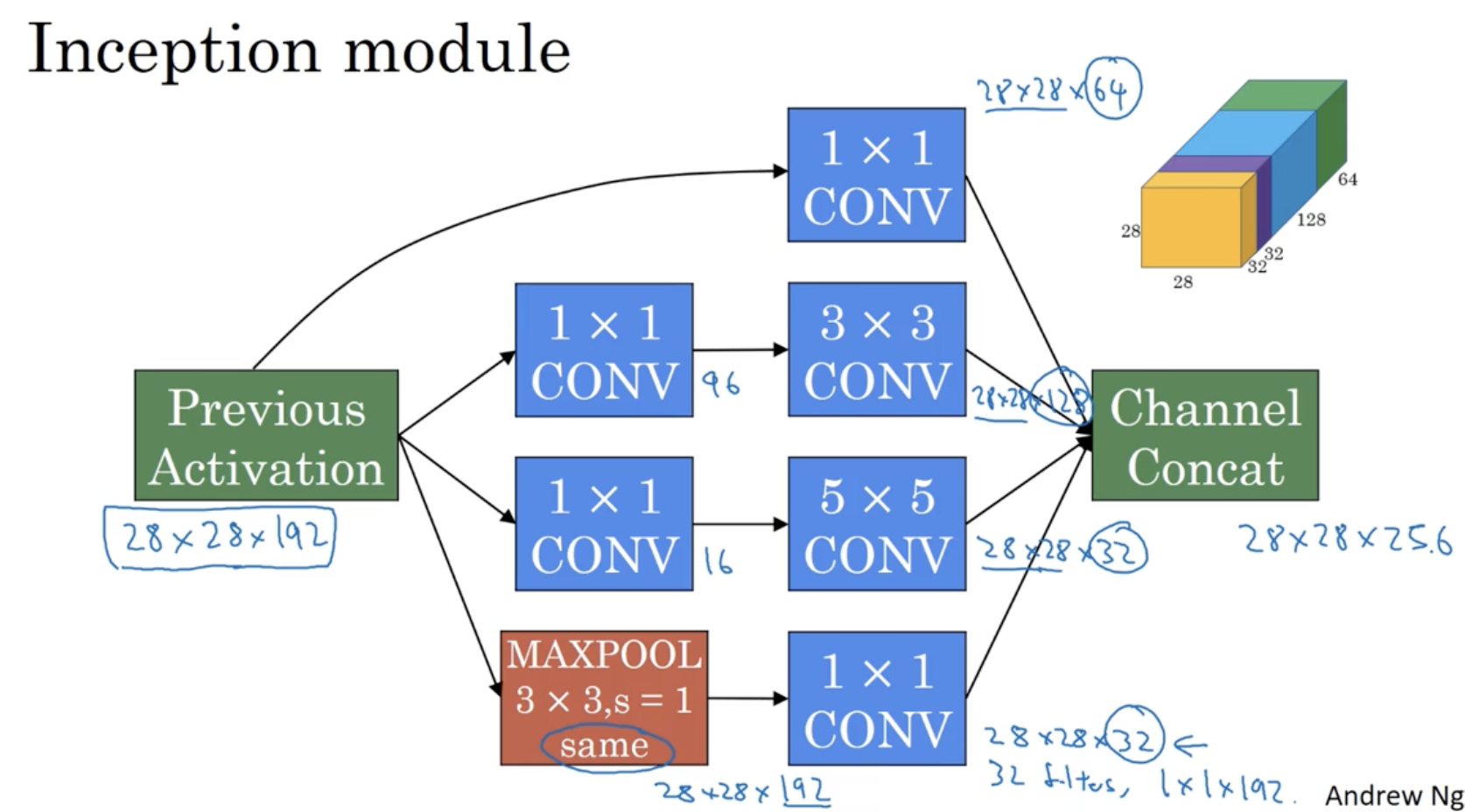
Inception Layer의 예시는 아래와 같다.

• 1 x 1, 3 x 3, 5 x 5 conv. layer와 max pooling layer를 적용하여 64, 128, 32, 32 차원을 갖는 데이터를 하나로 합쳐 28 x 28 x 256 차원의 데이터를 만든다.
• 이때 각 layer에 적용되는 filter의 크기는 모두 28이라고 하자. (다만, max pooling의 경우 일반적으로 padding이 적용되지 않지만 이 경우에는 padding이 적용된다.)
  

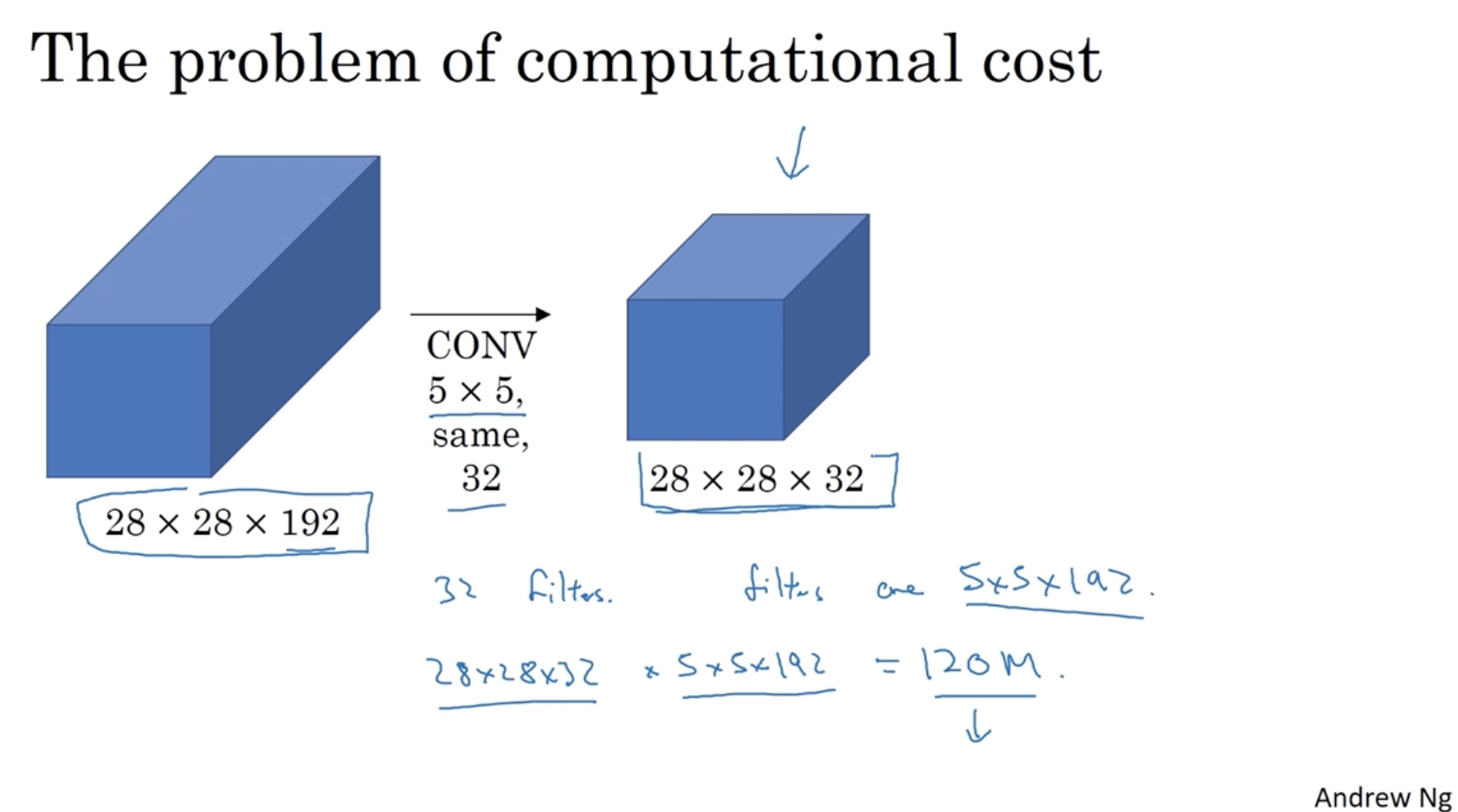
하지만 위와 같이 진행할 경우, 연산 비용이 매우 많이 든다는 단점이 존재한다.

• 예를 들어, 아까의 5 x 5 conv. 연산 비용을 계산하면 다음과 같다.
• ouput 값인 28 x 28 x 32 와 필터 크기 5 x 5 x 192를 곱하여
  $28 \times 28 \times 32 \times 5 \times 5 \times 192=120M$ 120만 개의 연산이라는 매우 큰 비용을 알 수가 있다.
  

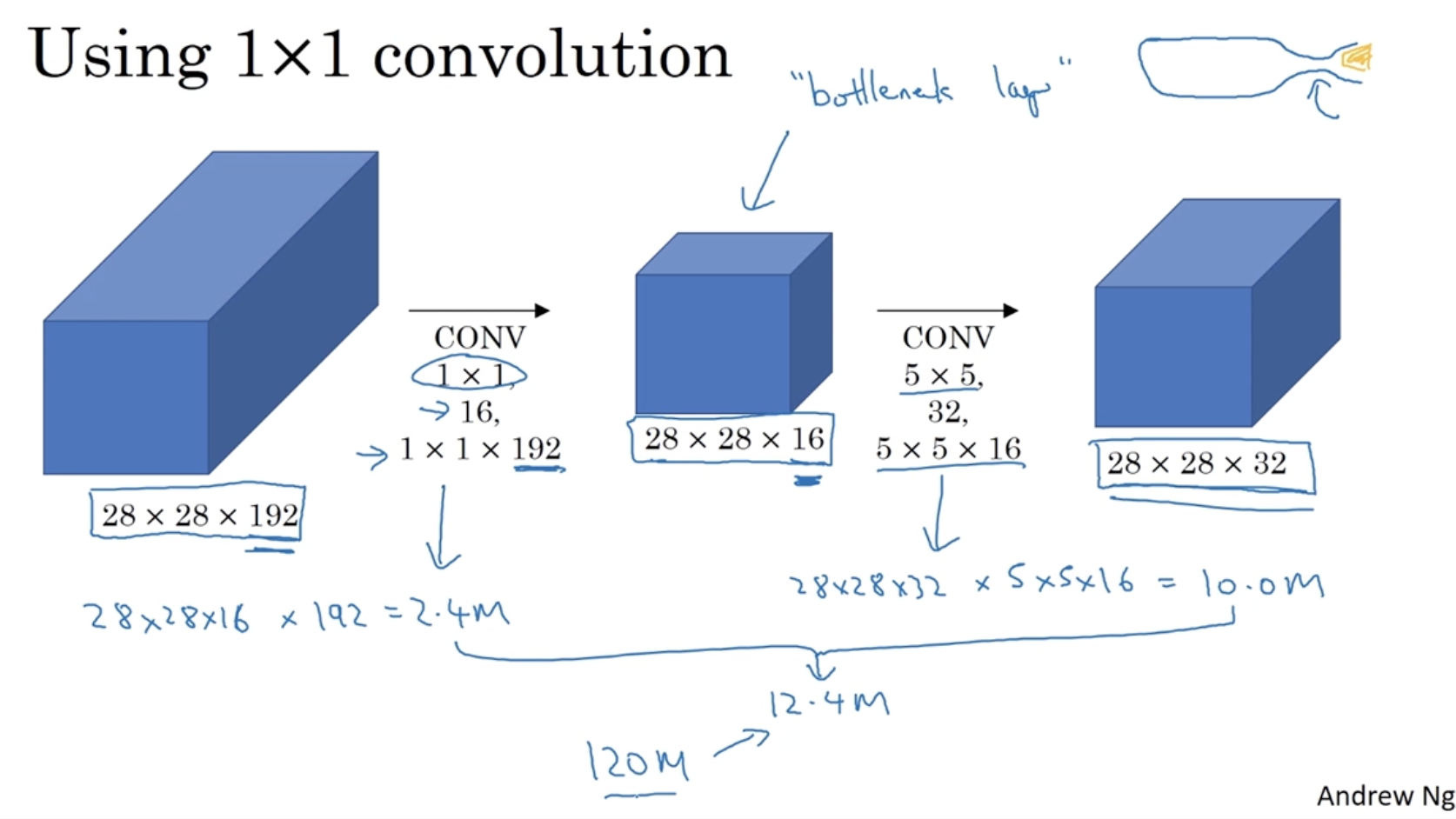
따라서 연산 비용을 줄이기 위해 1 x 1 conv.를 적용한다.

• 아래와 같이 중간에 "bottleneck layer"를 추가하여 채널 수를 줄일 수가 있다.
• 아래와 같이 연산 비용을 앞에서부터 계산하여 총 연산 비용을 계산했을 때, 12.4M이라는 값이 나온다.
• 아까의 120M 과 12.4M 을 비교했을 때 연산 비용이 크게 줄었음을 확인할 수가 있다.
  

---

따라서 Inception module의 구조는 아래와 같이 정리가 가능하다.

• conv. 에 대해서는 1x1 conv.인 bottleneck layer를 추가하여 연산 비용을 줄인 후 각각의 output을 구하고, max pooling 에 대해서는 max pooling을 적용한 후 1x1 conv. bottleneck layer를 추가한다.
• 그리고 각각의 output을 concatenate하여 하나의 output으로 만든다.
• 이게 하나의 Inception module이다.
  

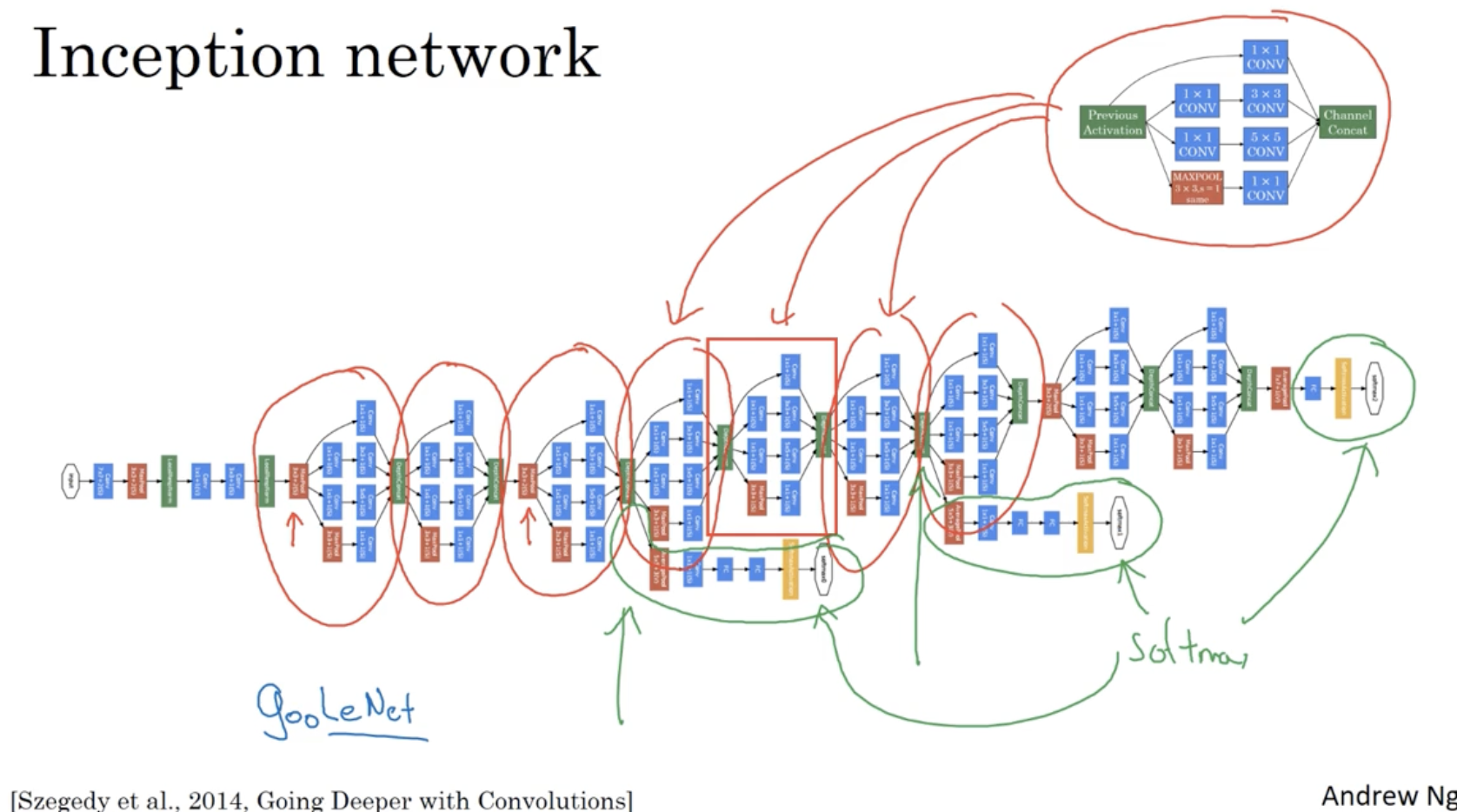
그리고 Inception network 은 다음과 같은 구조를 띈다.

• 쉽게 생각해서 여러 Inception moudle이 반복되는 구조를 띈다.
• 다만, 중간 히든 레이어에 FC-softmax 레이어가 있는데 이는 모델의 경과를 확인하기 위한 일종의 디버깅 용도로 사용된다고 한다.
  

---

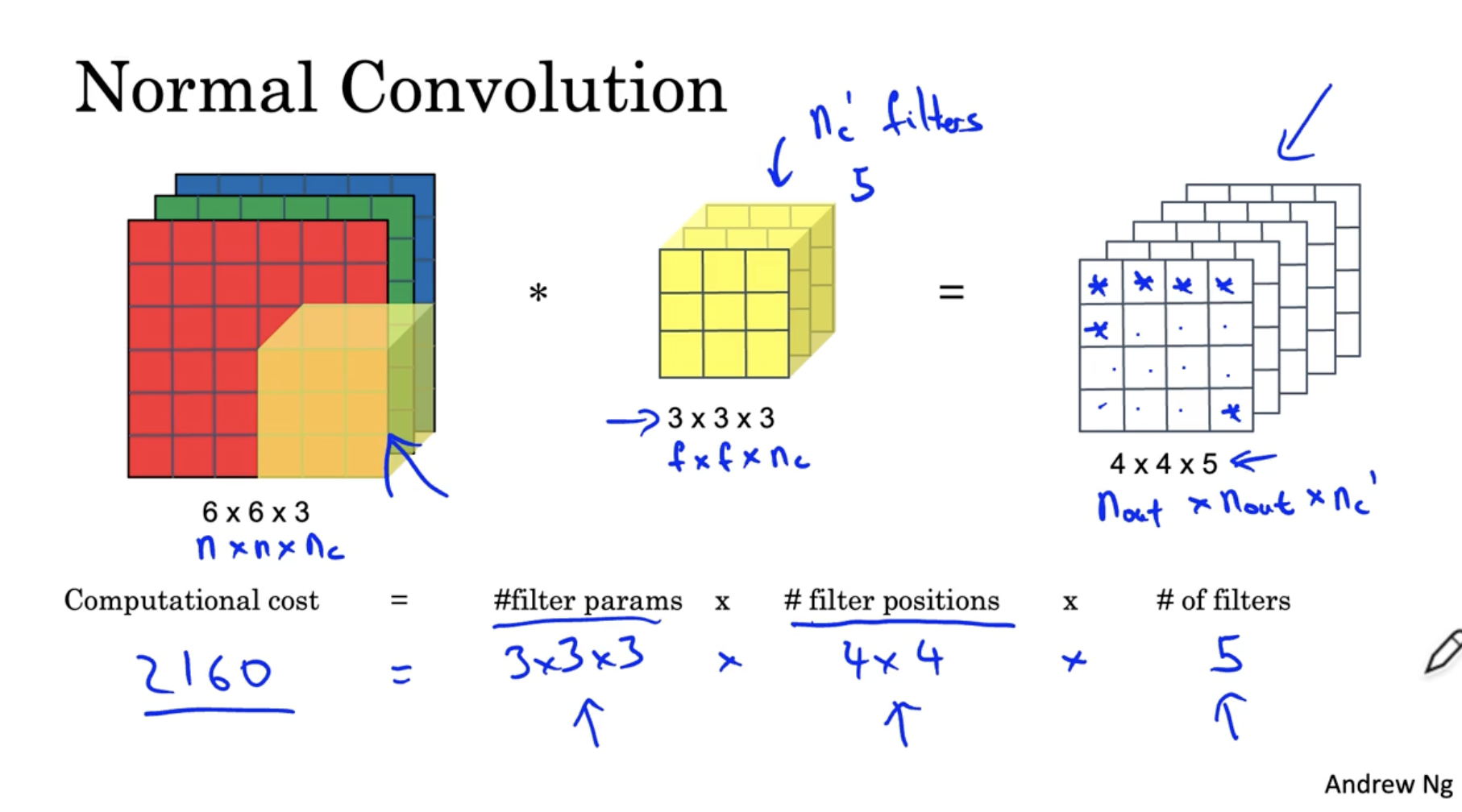
일반적인 Convolution 연산은 아래와 같다.

• 아래 예시의 경우 총 비용이 2160이 든다.
  

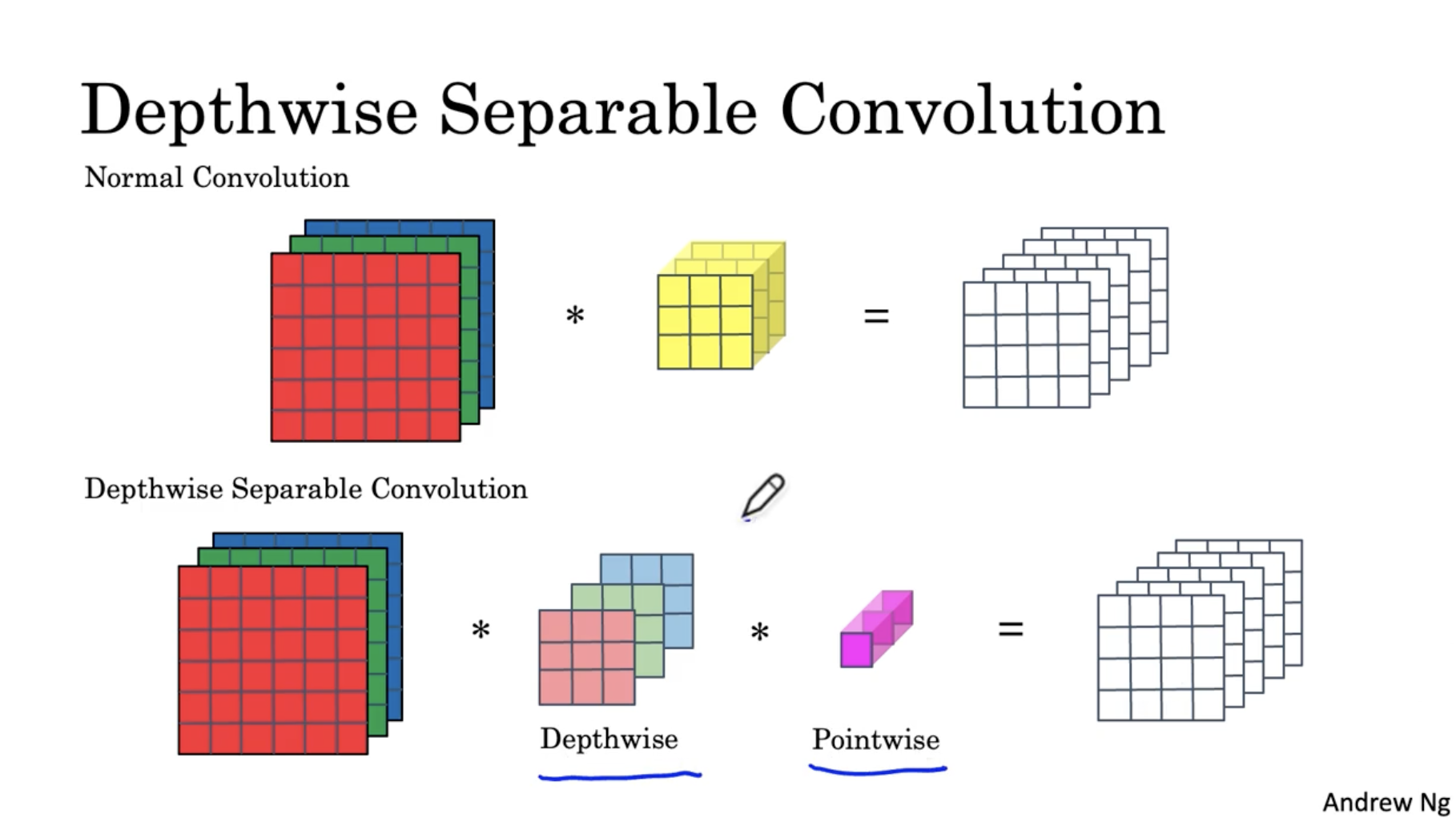
그렇다면 이러한 normal convolution을 depthwise + pointwise 두 개로 나눠서 연산하면 어떨까?

• normal convolution 과 depthwise separable convolution 은 과정만 다르고 결과는 같게 나온다.
• 한번 비교를 해보자.
  

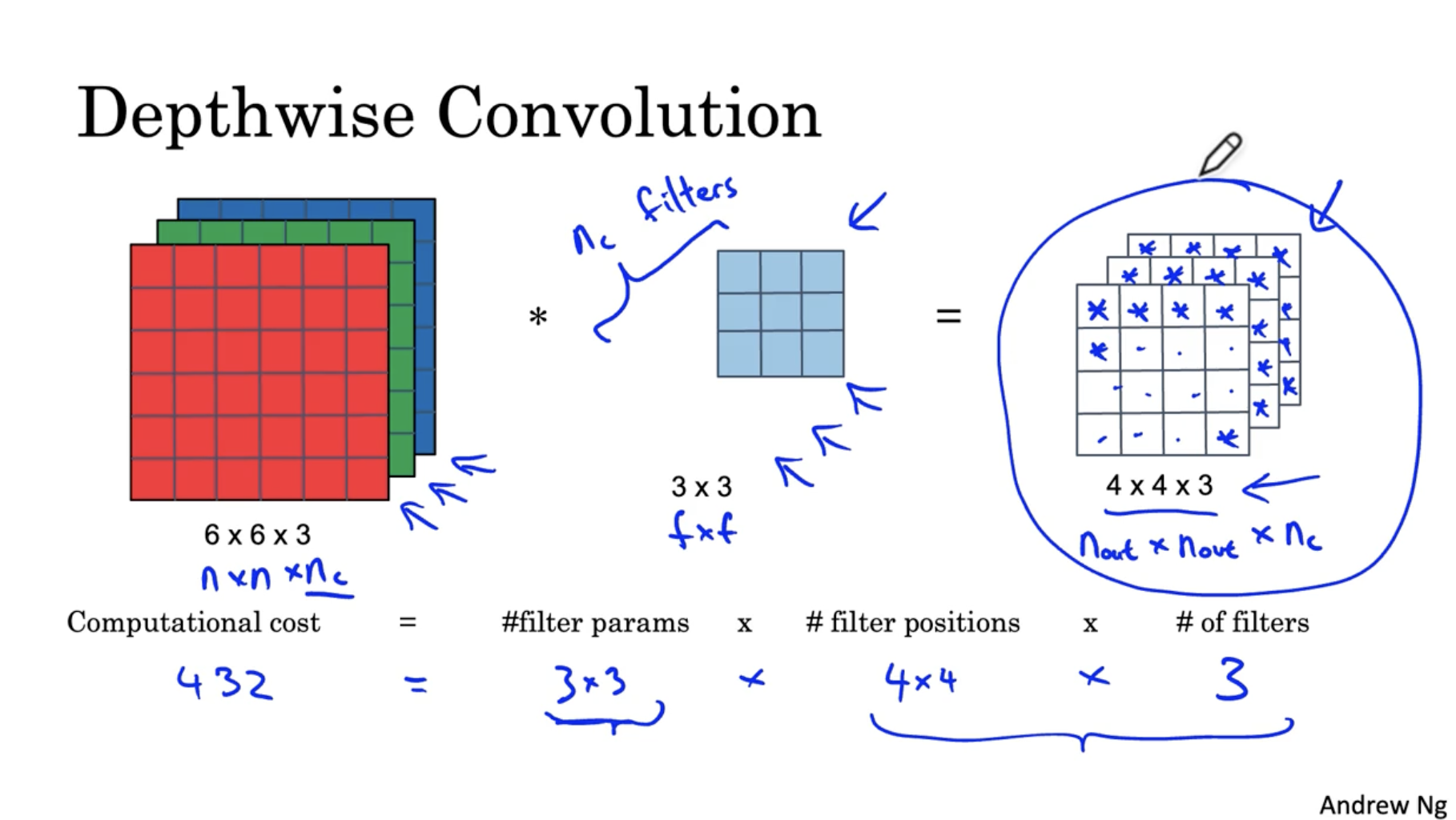
depthwise convolution의 depthwise 단계는 아래와 같다.

• filter 크기는 3 x 3 ($f \times f$) 으로 되어 있고, 대신 filter의 수($n_c$)가 3개이다.
• 각 filter는 각 R, G, B에 대해서 conv.를 수행한다.
• 그러면 그 결과는 $4\times 4 \times 3$로 나올 것이다.
• 이 경우 총 연산 비용을 계산해보면 432가 나온다.
  

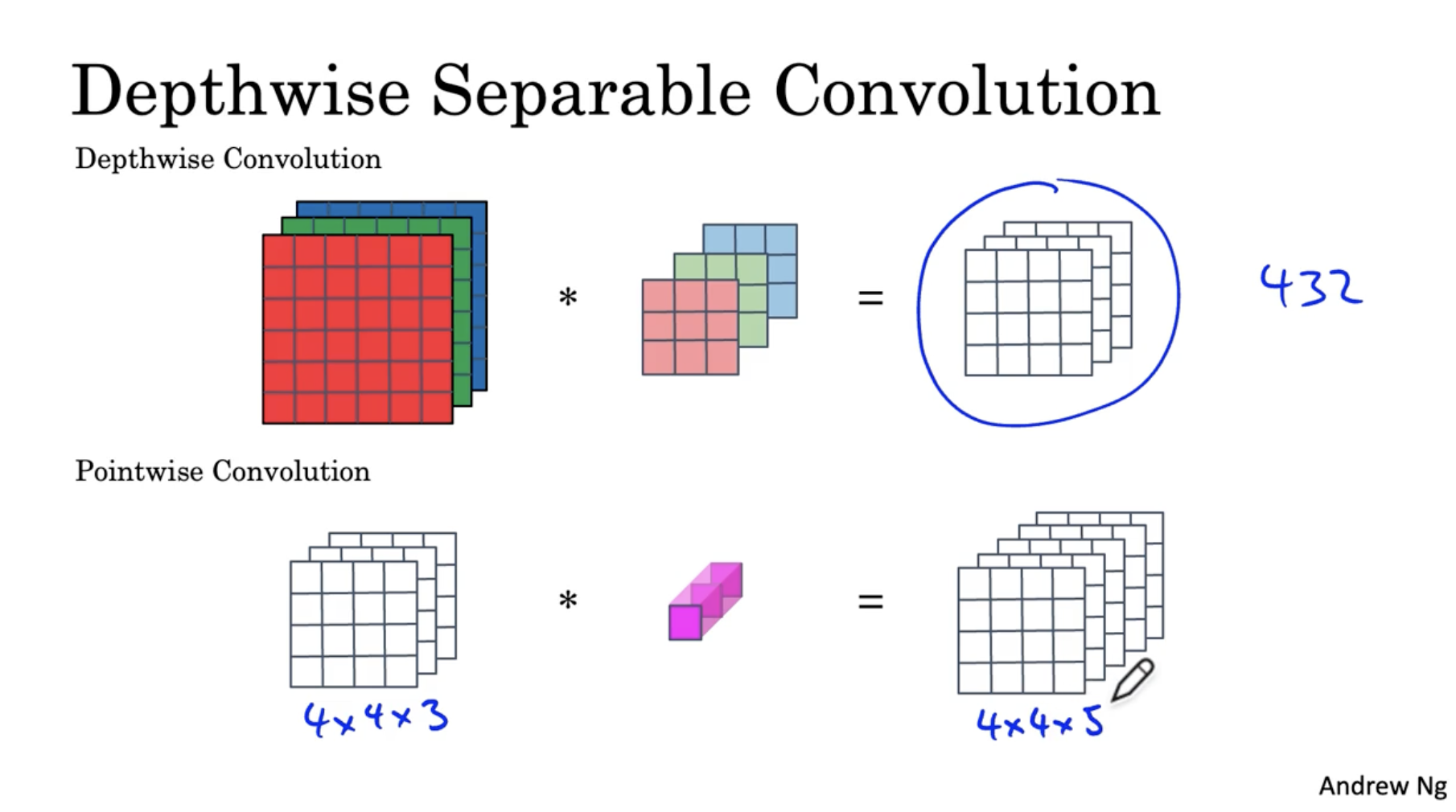
이제 다음으로 pointwise 연산을 진행해본다.

• 아래와 같이 depthwise 단계의 output인 4 x 4 x 3 데이터를 가지고 pointwise 단계를 수행한다.
  

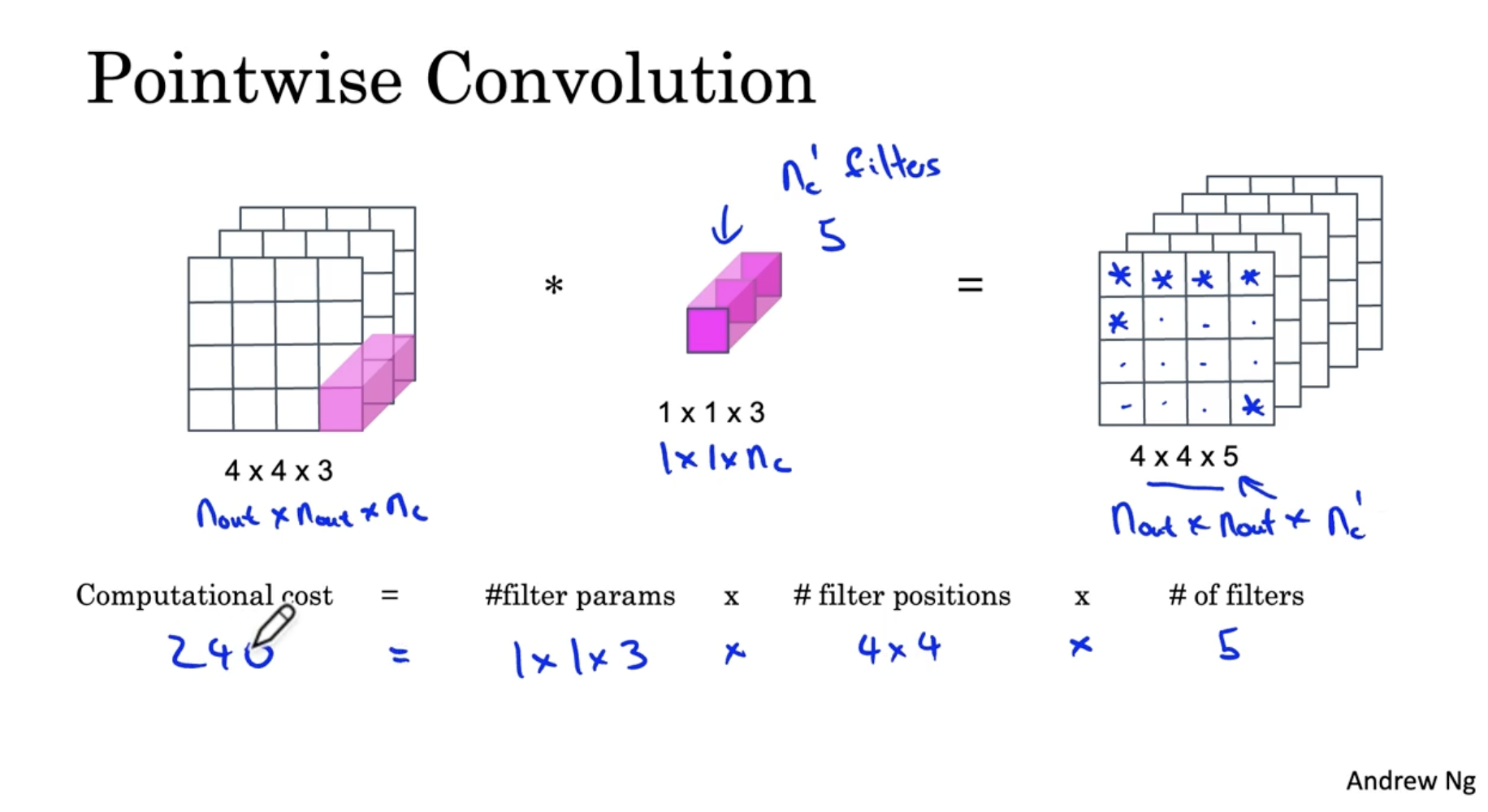
pointwise conv. 예시는 아래와 같다.

• 4 x 4 x 3 데이터에 대해서 1 x 1 x 3 포인트 필터를 적용한다. 그리고 이 포인트 필터의 수($n_c$)는 5개이다.
• 4 x 4 x 3 데이터 5개의 필터를 각각 적용하여 4 x 4 x 5 output을 얻는다.
• 이 경우 연산비용은 240이다.
  

따라서 normal conv. 와 depthwise separable conv.를 비교했을 때, 연산 비용은 아래와 같다.

• normal conv. : 2160
• depthwise separable conv. : depthwise + pointwise = 432 + 240 = 672
• 그리고 normal이 depthwise보다 31% 연산 비용이 많이 든다는 것을 확인할 수 있었다.
• 그리고 이를 수식으로 정리하면 $\frac{1}{n_c'}+\frac{1}{f^2}$이다. ($n_c'$은 normal conv.에서의 filter 수를 의미, $f$는 필터 길이를 의미) ($0.31 \approx \frac{1}{5} + \frac{1}{9}$)
• 그리고 만약 filter 수가 512개에 filter 길이가 3이라면, $\frac{1}{512}+\frac{1}{3^2} \approx 0.1$이 되어 depthwise seperable conv.가 normal conv.보다 10% 가량 더 연산 비용이 낮다는 것을 예측할 수 있을 것이다.
  

---

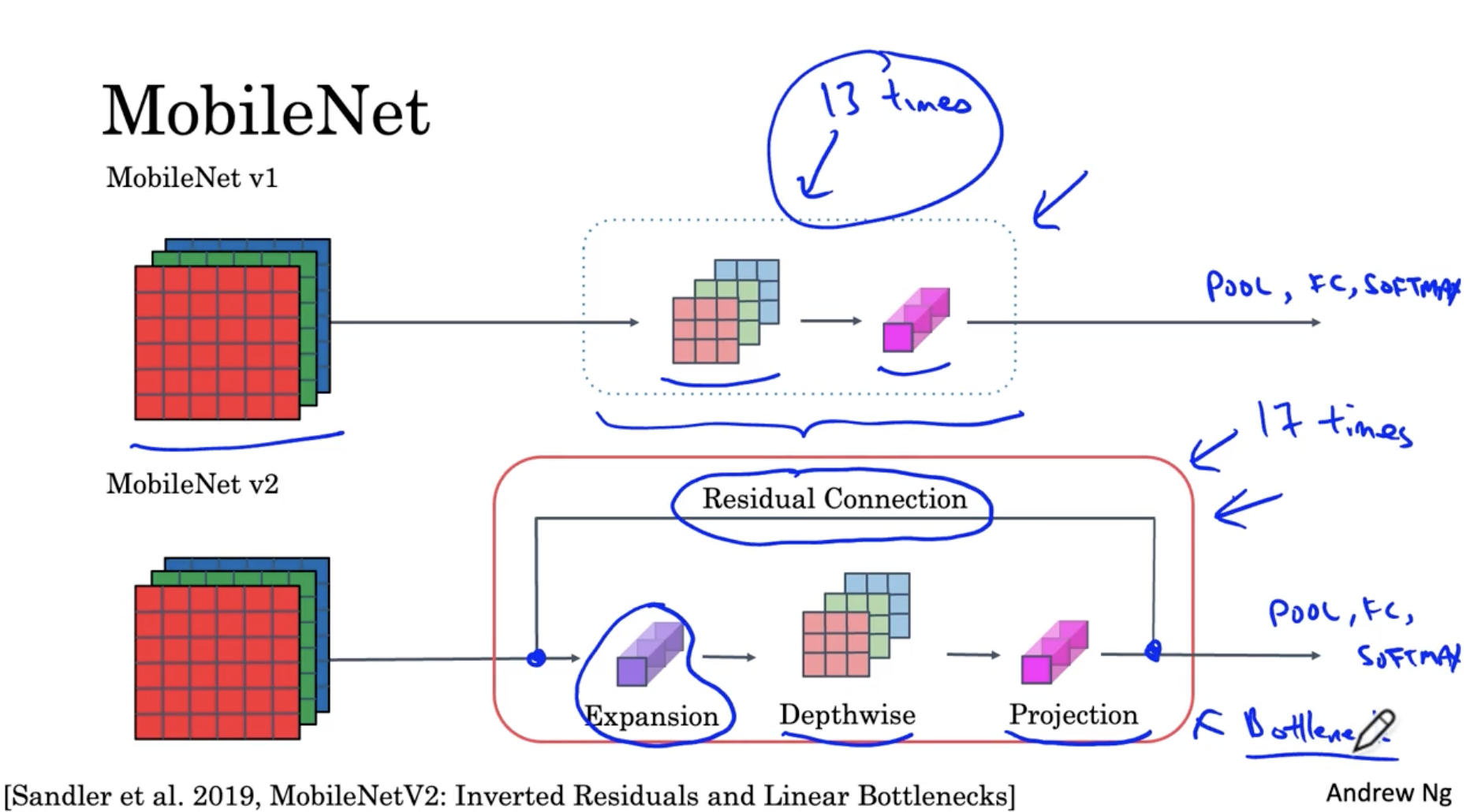
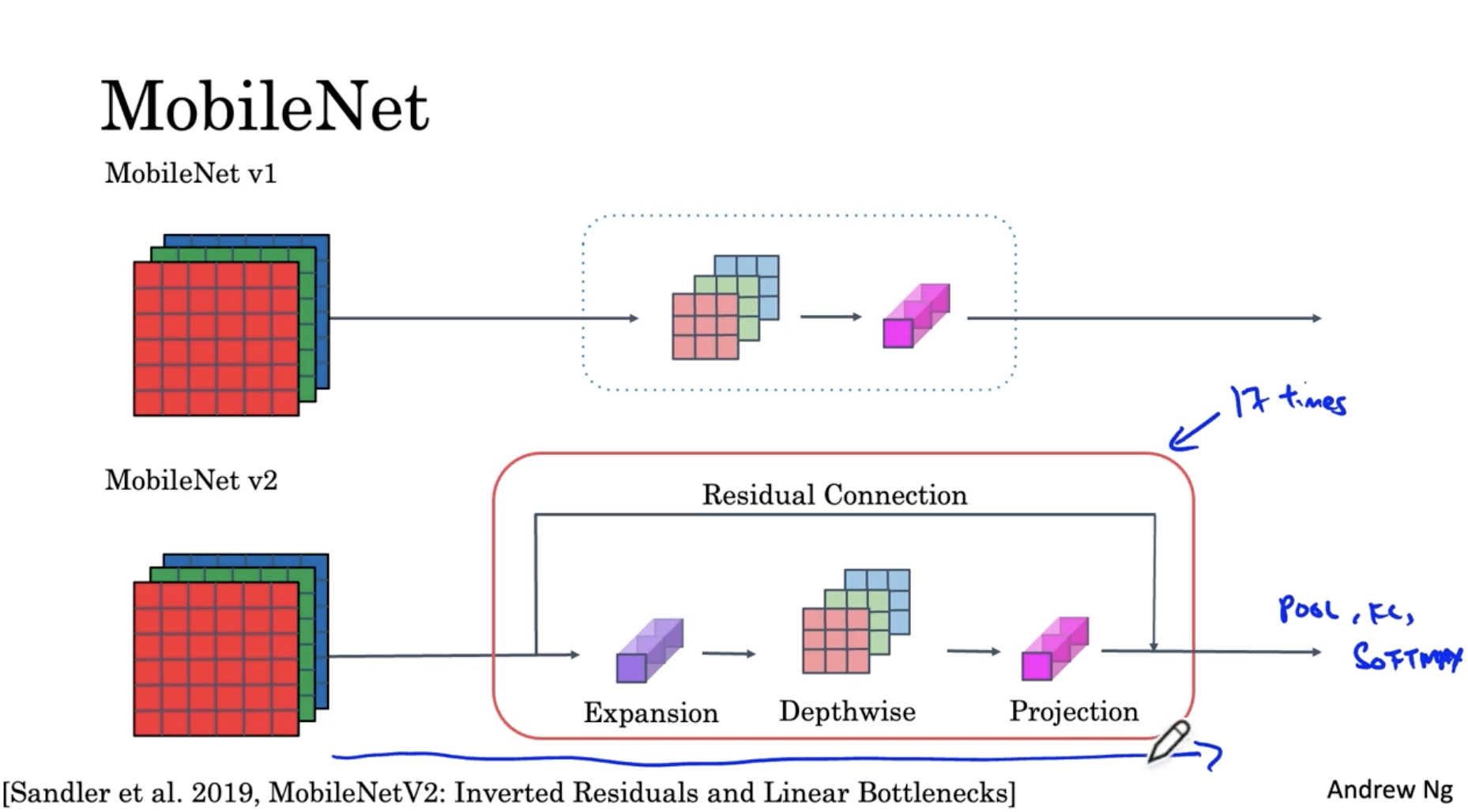
MobileNet은 mobile phone과 같이 메모리가 적은 경우 적용할 수 있는 CNN 기반 모델이다. MobileNet의 구조는 아래와 같다.

• MobileNet v1의 경우 13개의 depthwise seperable conv. 이후 pool, FC, softmax layer가 적용된 구조를 띈다.
• 반면에 MobileNet v2의 경우, "Residual Connection과 Expansion -> Depthwise -> Projection(=pointwise)" 로 이뤄진 bottleneck block이 17번 반복되고 이후 pool, FC, softmax layer가 적용된 구조를 보여준다.
  

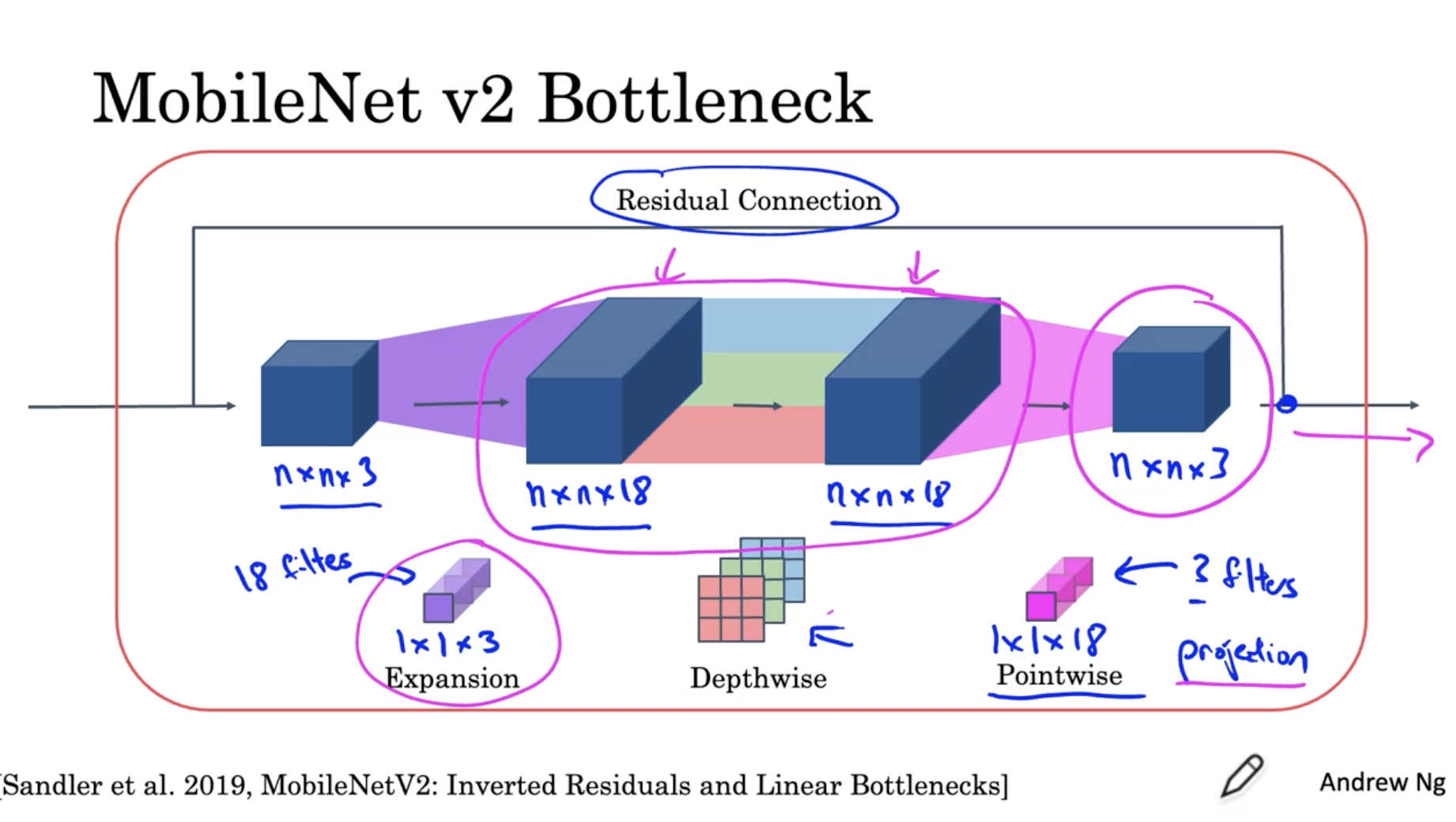
bottleneck block의 자세한 구조는 아래와 같다.

• expansion : n x n x 3 데이터에 대해서 18개의 1 x 1 x 3 필터를 적용하여 n x n x 18 데이터로 확장한다.
• depthwise : n x n x 18 데이터에 대해서 depthwise conv.를 적용하여 많은 weights들을 학습한다.
• pointwise(=projection) : n x n x 18 데이터에 대해서 3개의 1 x 1 x 18 필터를 적용하여 n x n x 3 데이터로 축소한다. (왜냐하면 edge device의 경우 메모리 리소스가 부족하기 때문에 데이터를 축소할 필요가 있다.)
• residual : 그러고 나서 이전의 데이터 $a^{[l-2]}$를 추가한다.
• 결론적으로 이러한 bottleneck block을 적용함으로써, depthwise에서는 더 많은 weights 들을 효과적을 학습할 수가 있고, pointwise에서는 데이터를 축소하여 리소스를 아낄 수가 있다.
  

따라서 개략적인 MobileNet의 구조를 이해할 수 있었다.

---

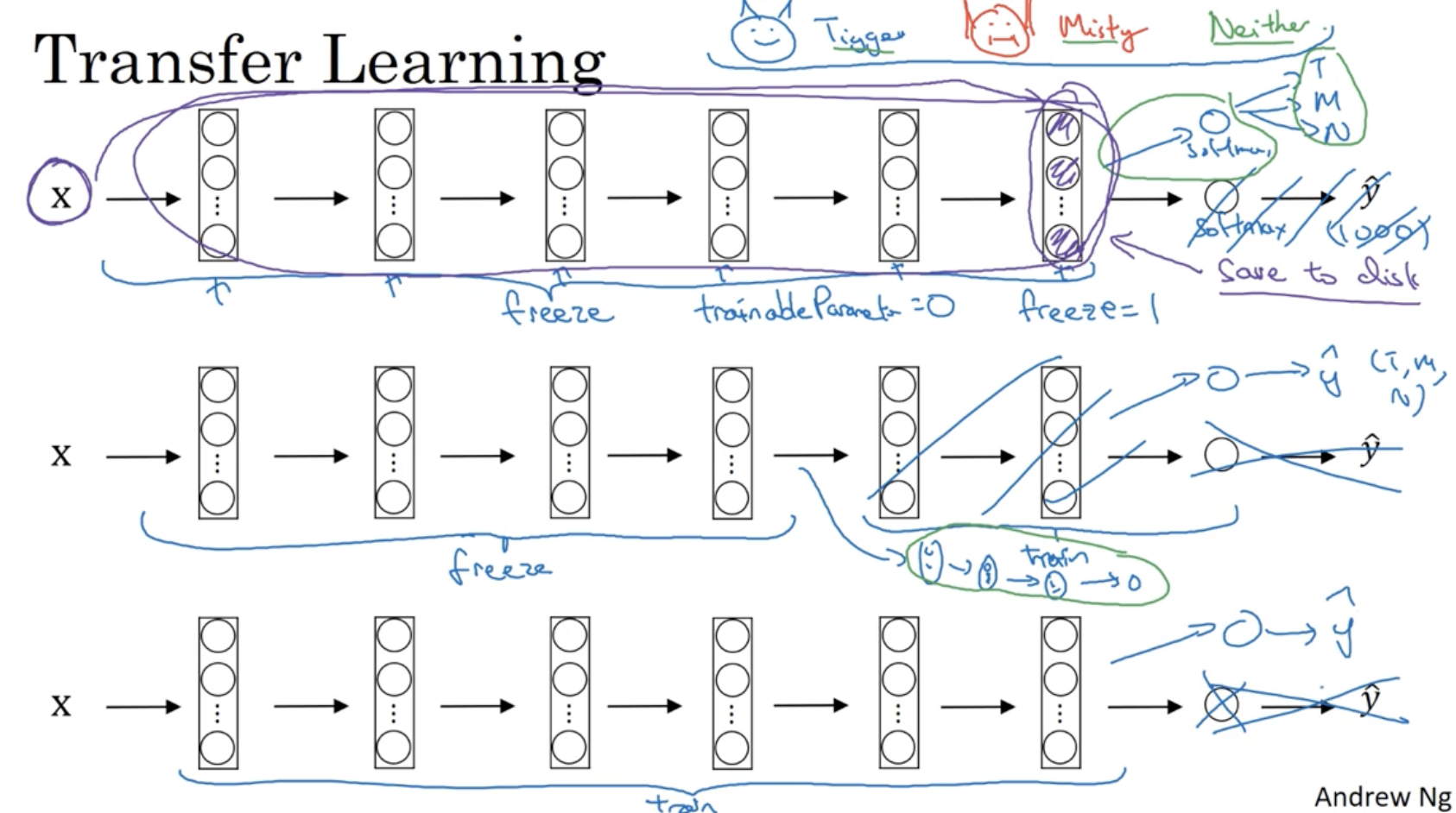
보통 딥러닝 모델을 scractch한 방식으로 처음부터 구현하기 보다는 기존의 모델의 파라미터와 구조를 가져와서 필요한 데이터를 학습하는 식으로 활용한다. 이를 Transfer Learning 이라고 한다.

• 예를 들어, 본인만의 특정한 데이터에서 [Tigger, Mity, Neither] 3개의 class를 분류한다고 가정해보자.
• 이 경우 ImageNet과 같은 이미지 분류 모델의 정보를 가져와서 여기에 저만의 데이터를 적용하면 된다. 다만 ImageNet의 경우 마지막 softmax의 차원의 (1000, 1)이라서 이를 위 데이터에 맞게 (3, 1)으로 수정할 필요가 있다.
• 즉, softmax layer만 수정하고, 나머지 layer들은 freeze해 놓는다. (학습 적용X, 학습된 weight로 고정) 이를 코드에서 구현하면 trainableParameter = 0 혹은 freeze = 1으로 세팅하면 된다. 그리고 softmax layer에 대해서만 학습을 진행하면 된다.
• 또 다른 방법으로는 softmax layer와 바로 이전의 몇 layer들만 학습하는 방식이 있다.
• 또 다른 방법으로, 모델의 구조만 그대로 가져오고 모든 layer를 처음부터 다시 학습시키는 방법도 있다.
  

---

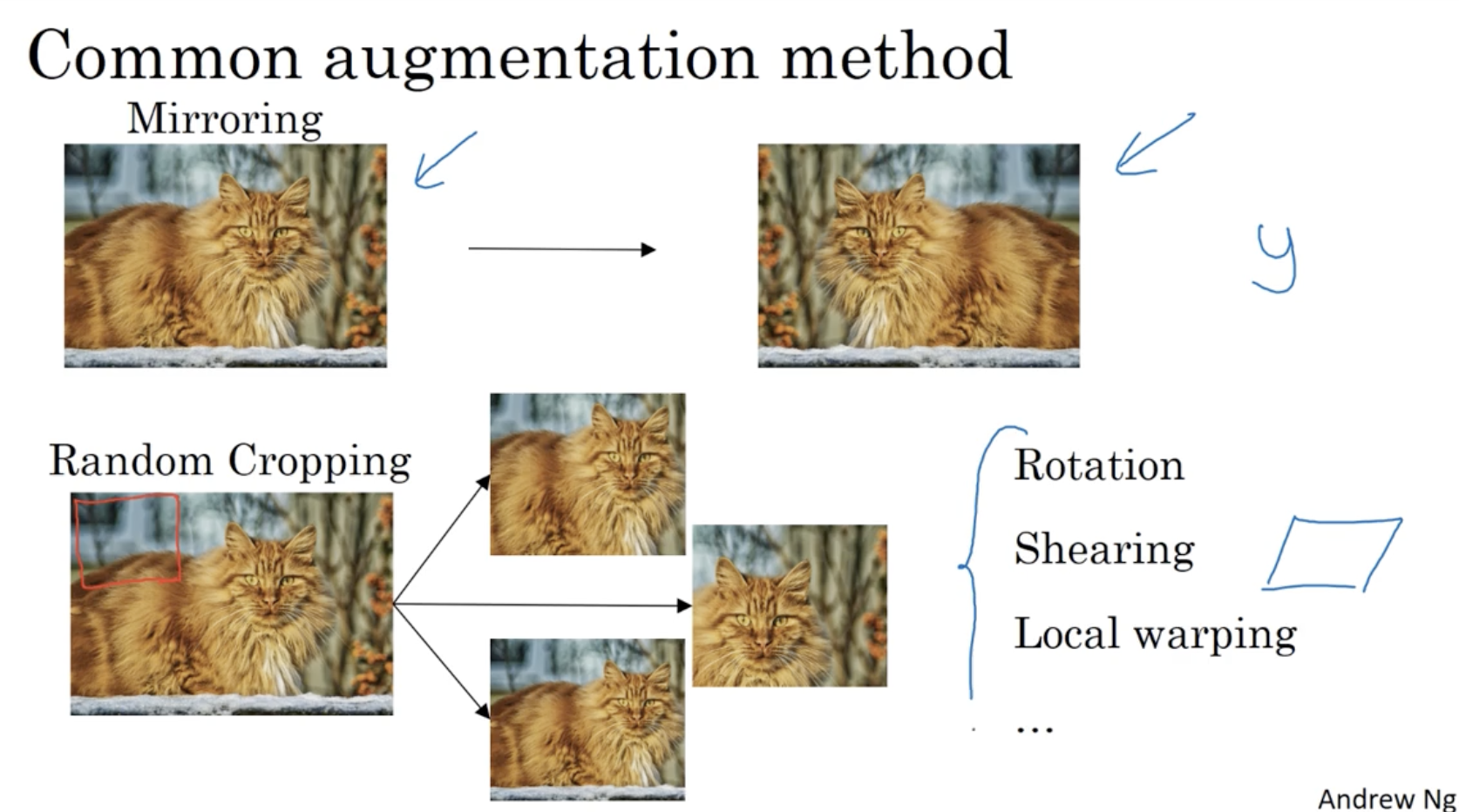
일반적으로 데이터를 수집하는 것은 매우 어렵다. 따라서 Data augmentation 방법을 적용하여 학습 데이터 셋을 늘려주는 것이 필요하다.

• 아래는 일반적인 data augmentation의 예시이다.
  

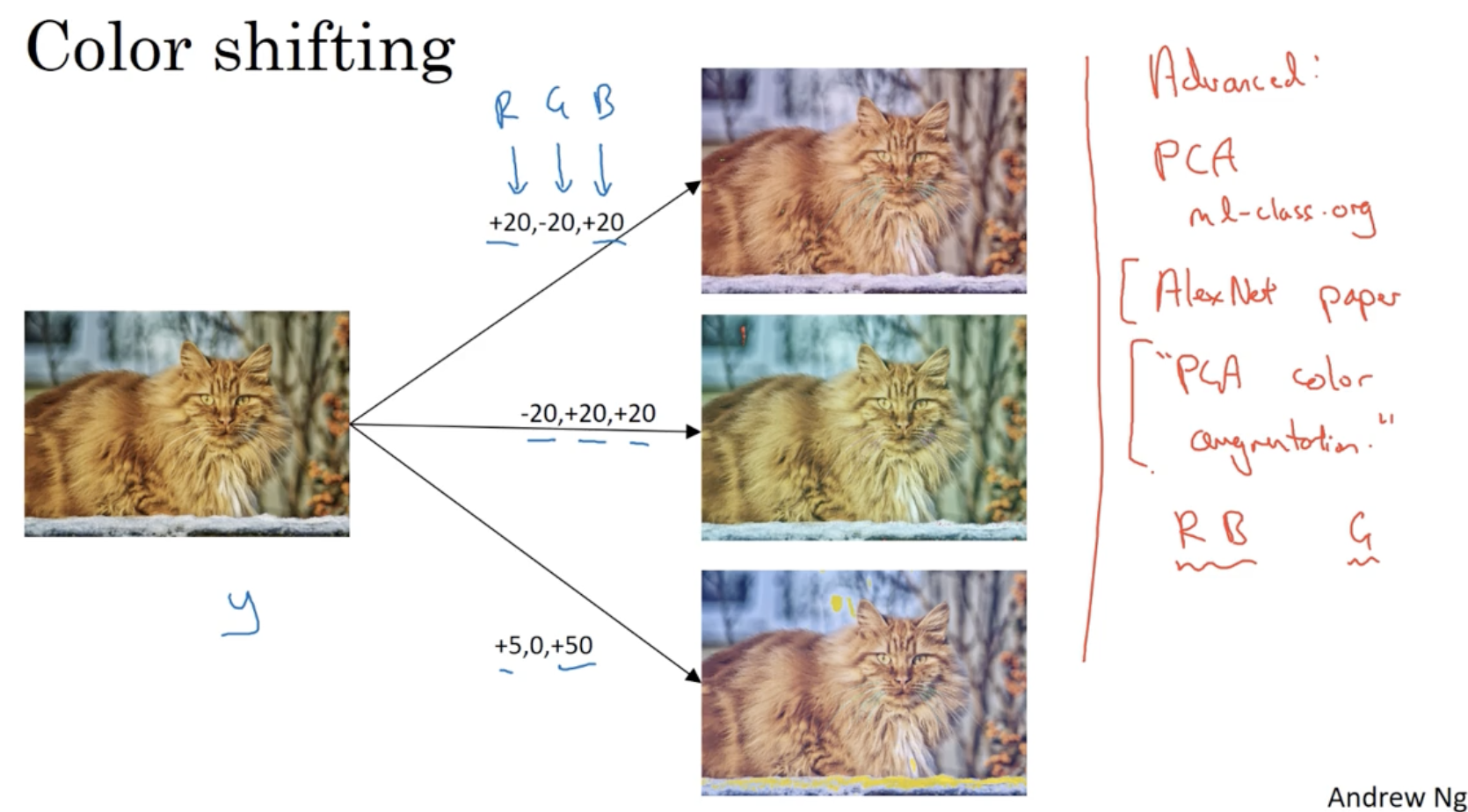
또한 color shifting과 같이 간단한 data augmentation도 존재한다.

• 그리고 PCA color Augmentation 과 같이 복잡한 augmentation 모델도 존재하는데, 보통 이러한 코드는 오픈소스에 구현되어 있어 찾아서 그대로 적용하면 된다.
  

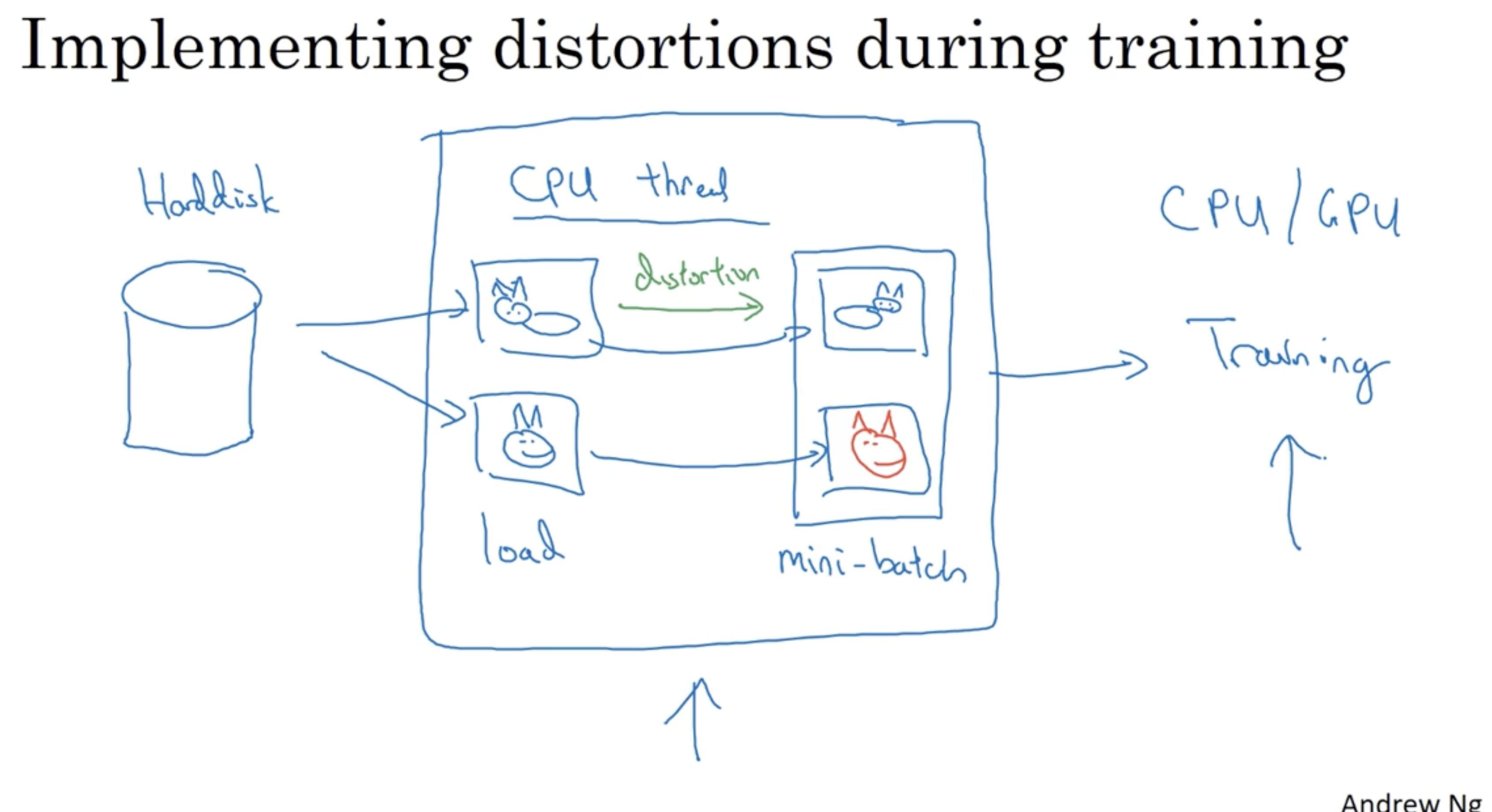
학습할 동안 disk에서 이미지를 가져오고 distortion을 적용한 후 이를 mini-batch 데이터로 만든다. 그리고 이러한 두 과정은 서로 병렬로 처리되어 multiprocessing이 가능하다.

---

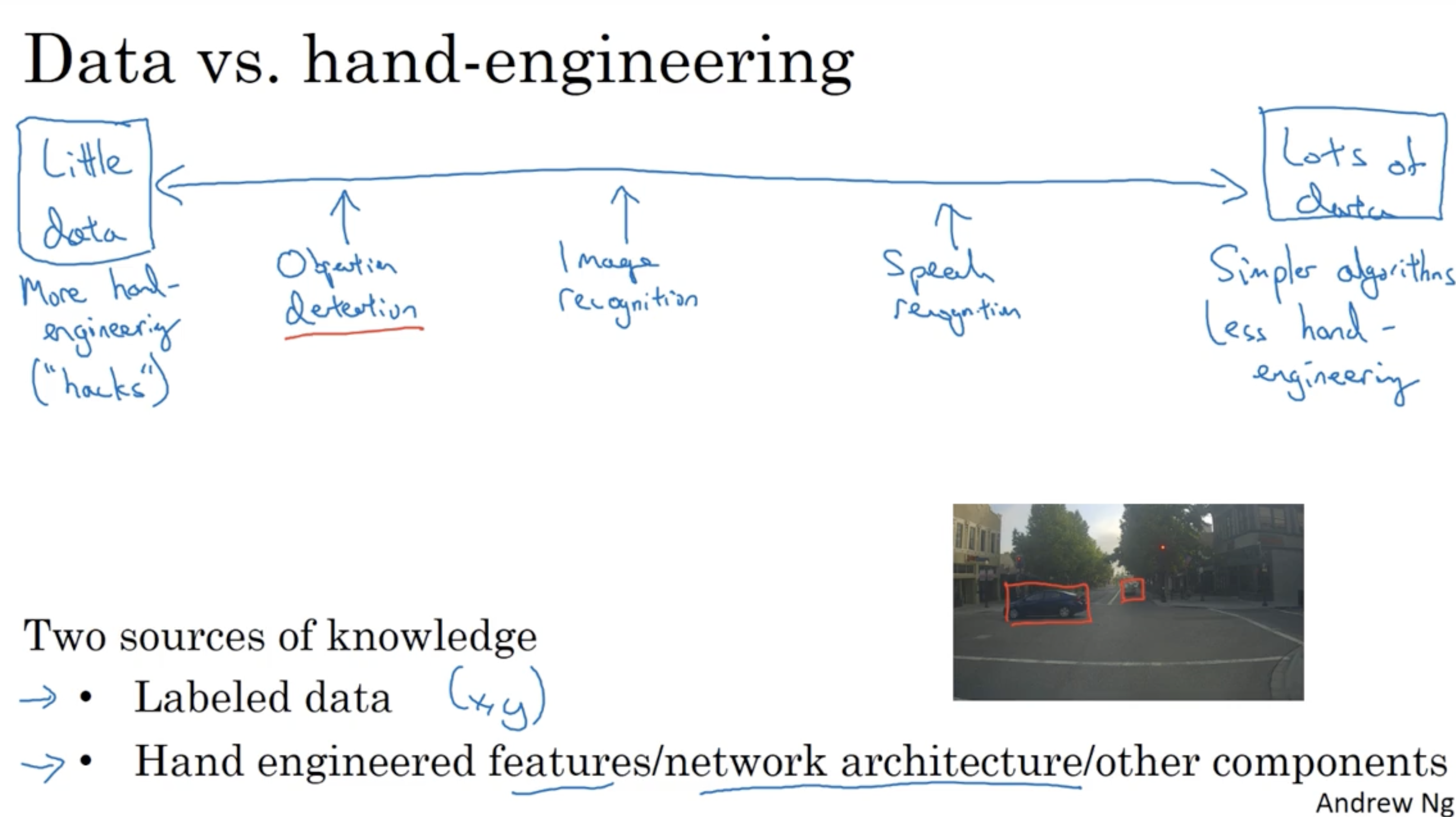
일반적으로 데이터가 많으면 모델이 대충 만들어지더라도 정확도가 높게 나오지만, 데이터가 적으면 모델을 정말 잘 만들어야 정확도가 높게 나온다.