[딥러닝] Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization Week 3

출처 : https://www.coursera.org/specializations/deep-learning

딥러닝 모델에는 아래와 같이 다양한 하이퍼파라미터가 존재한다. 그러면 어떻게 최적의 하이퍼파라미터를 찾을 수 있을까?

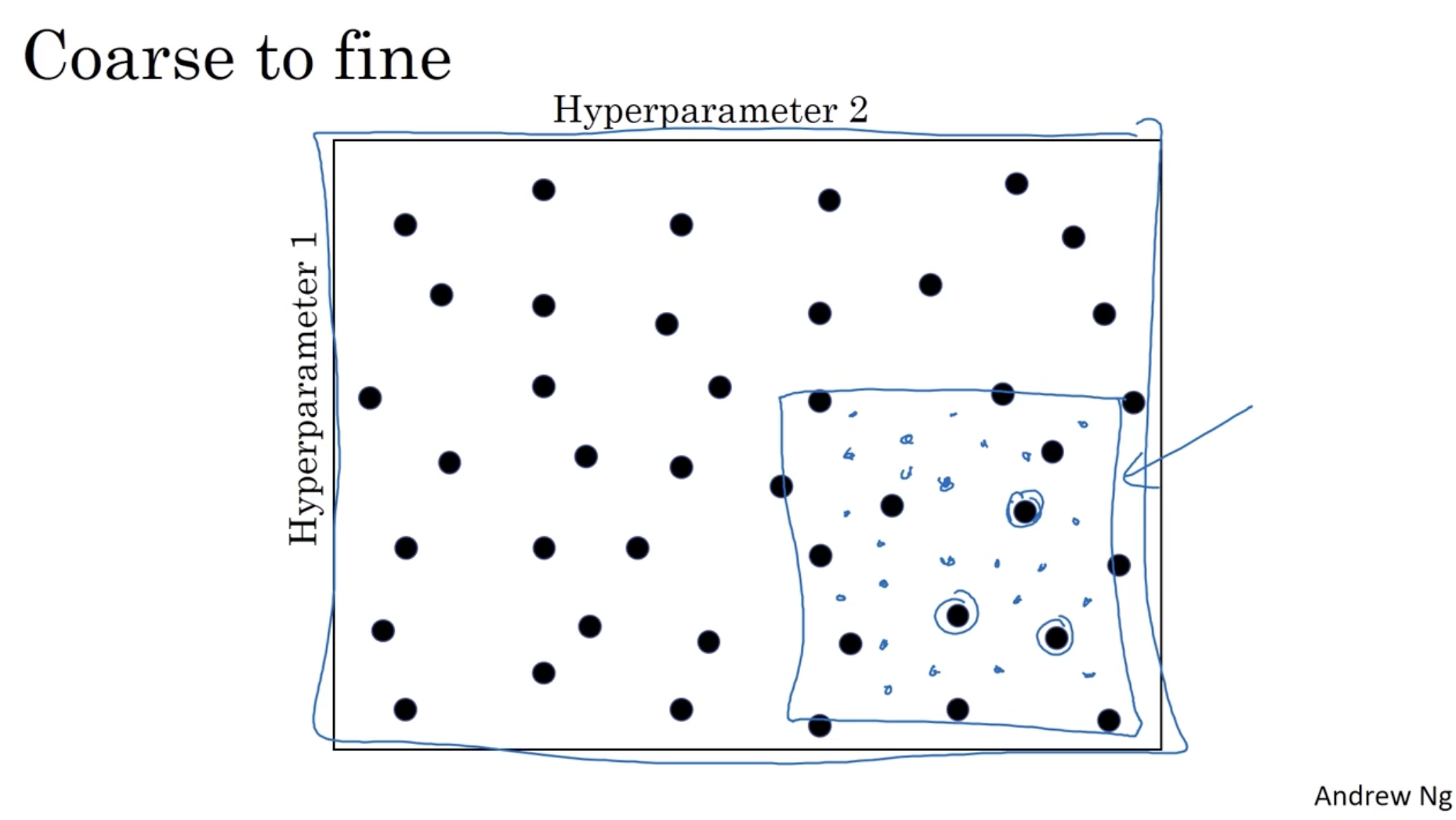
아래는 grid vs. random 에 대한 예시이다.

• 왼쪽과 같이 grid한 방식으로 하이퍼파라미터를 찾을 경우, learning rate $\epsilon$ 과 같이 값이 매우 작은 하이퍼파라미터의 영향은 거의 없어서 비효율적일 수 있다.
• 따라서 오른쪽과 같이 랜덤한 방식으로 하이퍼파라미터를 찾는 것이 더 효율적이다. (이는 하이퍼파라미터 차원이 늘어나도 마찬가지이다.)
  

또한 랜덤하게 하이퍼파라미터를 찾은 후, 그 주변을 좀 더 수색해서 최적의 하이퍼파라미터를 찾는 방법도 있다.

---

하이퍼파라미터마다 적절한 범위를 지정해주는 것은 중요하다.

• 아래 예시처럼 learning rate $\alpha$에 대하여 0.0001 ~ 1 까지의 범위를 지정한다고 해보자.
  • 이 경우, uniform하게 값을 분포시켜도, 90%가 0.1~1의 값을 갖고, 0.0001~0.1은 10%밖에 되지 않는다. 따라서 이는 부적절한 방법이다.
• 그렇다면 위와 달리 log 지수를 활용해보자.
  • 4개의 범위로 나눌 경우. $r=-4*np.random.rand()$, $r \in [-4,0]$
  • $\alpha=10^r$, $\alpha \in [10^{-4}, 10^0]$
  • 따라서 "0.0001 ~ 0.001", "0.001 ~ 0.01", "0.01 ~ 0.1", "0.1~1" 총 4개의 scale에 대하여 uniform하게 적용된 값들의 분포를 얻을 수 있다.
    

$\beta$와 같은 exponentially weighted averages 하이퍼파라미터에도 적용해보자.

• $\beta=0.9,...,0.999$ 의 범위를 갖는다고 해보자. 마찬가지로 바로 0.9~0.999로 나누지 않고, "0.9 ~ 0.99", "0.99 ~ 0.999"로 나누어 uniform하게 나눈다.
• 마찬가지로 $1-\beta$도 scale을 나눈다. $1-\beta=0.1,...,0.001$
  • $r \in [-3, -1]$
  • $1-\beta=10^r$
  • $\beta=1-10^r$
• 다만 주의할 점이 있는데, 만약 $\beta=0.999$와 같이 1에 매우 가까운 수에서 $0.9995$로 값을 조금만 변화시키더라도 $\frac{1}{1-\beta}$ 식에 의해서 매우 많은 영향을 끼친다. ($0.9 \to 0.9005$는 영향 거의 없음.)
  

---

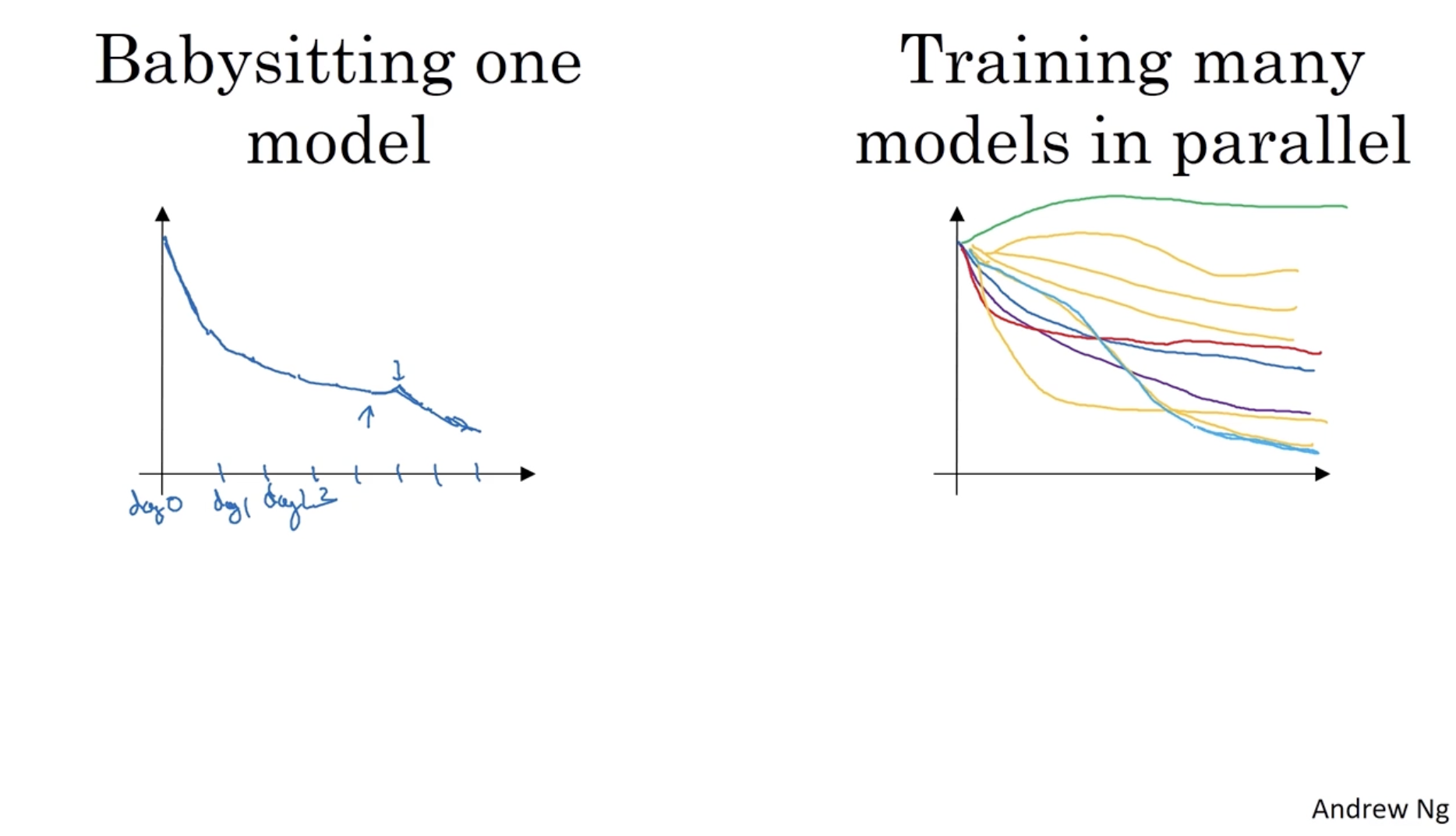
모델을 학습할 때 좌측과 같이 하나의 모델에 대해서 여러 날마다 모델을 학습하는 경우가 있고, 우측과 같이 여러 개의 모델을 동시에 학습하며 에러가 낮은 모델을 선택하는 방법이 있다.

• 만약 리소스가 충분하다면 우측과 같은 방법을 적용하면 효과적일 것이다.
  

---

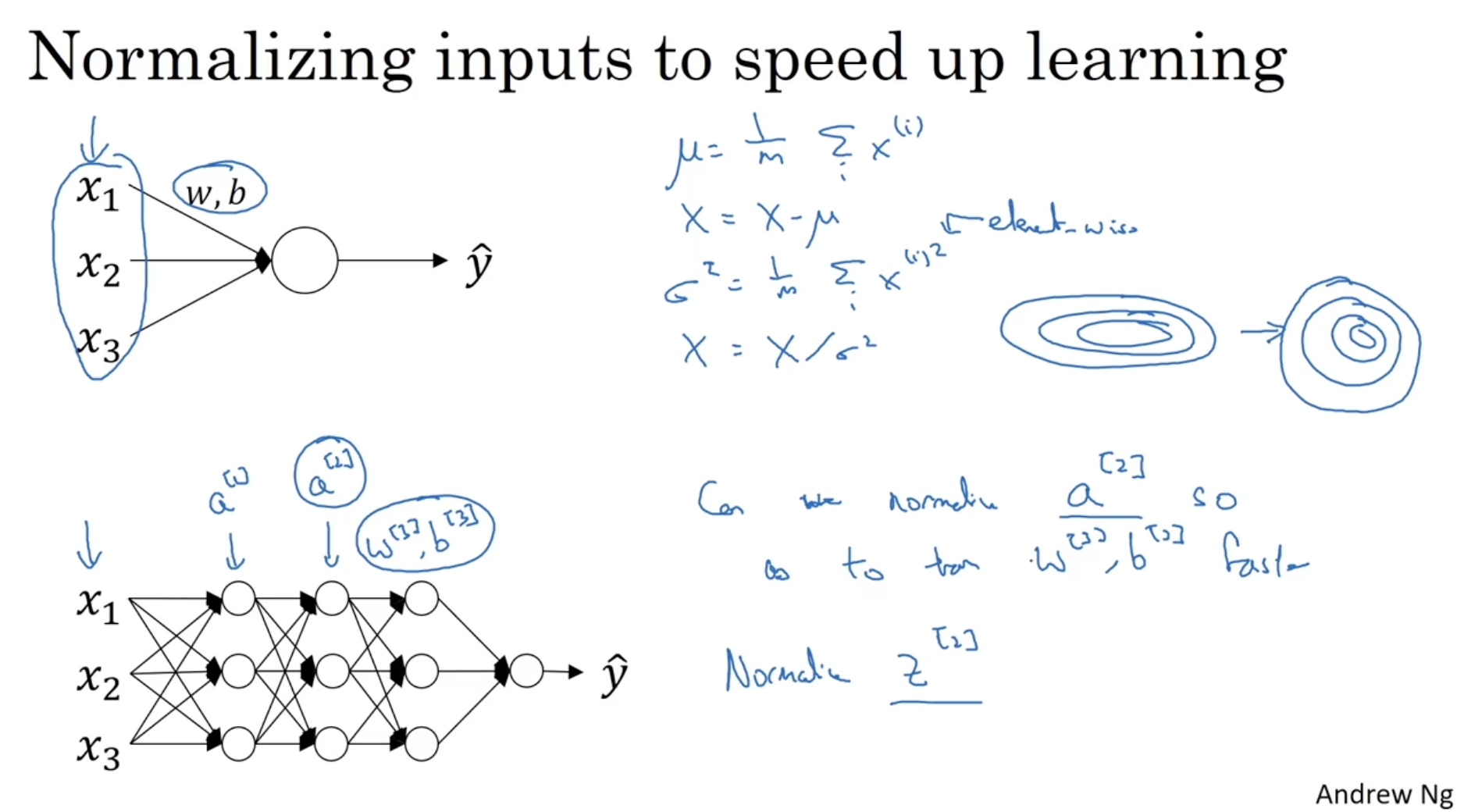
다음으로 batch normalization에 대해서 알아본다.

• 아래와 같이 입력 데이터 $X=\frac{X-\mu}{{\sigma}^2}$ 와 같이 normalization을 적용한다.
• 그러면 $a^{[l]}$ 을 normalization 할 수 있으며, 이로 인해 $W^{[l+1]},b^{[l+1]}$ 을 학습하는 데 속도가 빨라질 것이다.
  

그렇다면 $z^{[l]}$ 은 어떻게 normalization할 수 있을까. 아래를 보자.

• 마찬가지로 $z^{(i)}_{norm}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^2+\epsilon}}$ 과 같이 normalization을 적용한다. 하지만 이 경우 $N(0, 1)$ 로 데이터가 normalization 되므로 이를 방지하기 위해 아래와 같이 $\hat z^{(i)}$ 로 수정한다.
• $\tilde z^{(i)}=\gamma z_{norm}^{(i)}+\beta$ (여기서 감마와 베타는 모델이 학습가능한 파라미터를 의미한다.)
• 따라서 $z_{norm}^{(i)}$ 대신 $\tilde z^{(i)}$를 사용한다.
• 만약 $\gamma=\sqrt{\sigma^2+\epsilon}, \beta=\mu$ 라면 $\tilde z^{(i)}=z^{(i)}$가 된다.
• 만약 우측 하단의 그래프처럼 $z$ 값이 $N(0,1)$ 위주로 분포되어 있을 경우, sigmoid activation function의 경우 기울기가 항상 1로 나와 linear activation function을 띄어 학습이 잘 안될 수 있다. 그러므로 $z$에 normalization을 적용하여 평균 위치를 옮기거나 분산을 늘려야 한다.
  

---

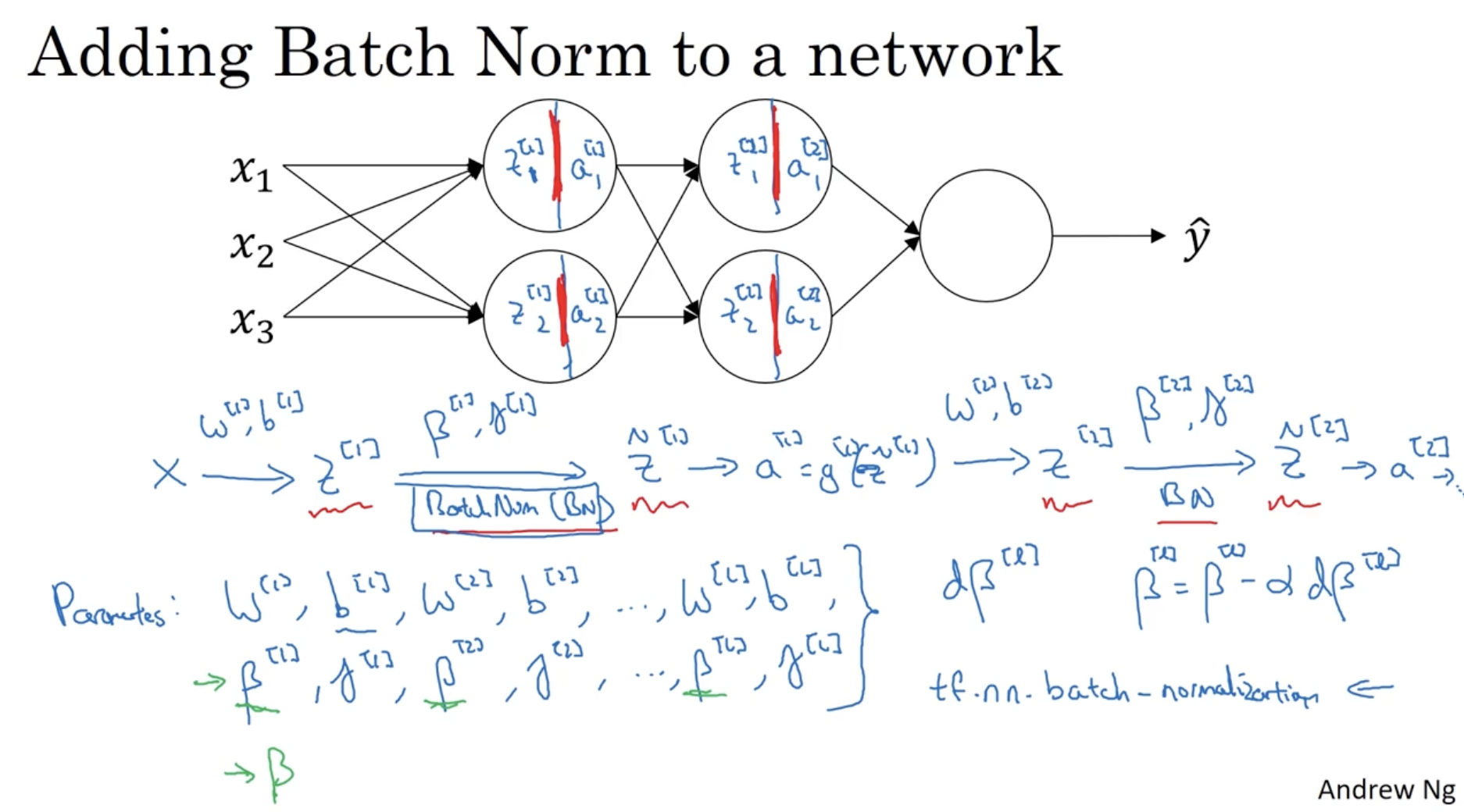
batch normalization을 NN에 적용하는 과정은 아래와 같다.

• 입력값 $x$에 대해서 $z^{[1]}$을 구한 후, $z^{[1]}$에 normalization(by $\beta^{[1]},\gamma^{[1]}$)을 적용하고 추가 과정을 거쳐 $\tilde z^{[2]}$를 구한다.
• 이런 식으로 레이어 $L$에 도달할 때까지 $z$에 norm.을 적용한다.
• 따라서 필요한 파라미터는 $W^{[1]},b^{[1]},\beta^{[1]},\gamma^{[1]},...,W^{[L]},b^{[L]},\beta^{[L]},\gamma^{[L]}$ 이다.
• 그리고 마찬가지로 $d\beta, d\gamma$를 통해서 gradient descent alg.을 적용할 수 있다.
• ex. $\beta^{[l]}:=\beta^{[l]}+\alpha d\beta^{[l]}$ (물론 momentum, RMSprop, Adam optimizer도 적용할 수 있다.)
  

mini-batch에 적용하는 것도 위와 거의 유사하다.

• 다만, 한 가지 디테일한 요소를 생각해보면, $z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$ 에서 $b^{[l]}$ 값이 변한다고 해도 분포의 모양은 바뀌지 않는다. 또한 $z^{[l]}$에 norm.을 적용할 때, $\beta$에 의해서 평균값의 위치를 조정할 수 있기에 $b^{[l]}$는 필요가 없다.
• 따라서 이 경우 $b^{[l]}$는 제외해도 괜찮다.
  

따라서 batch normalization의 구현 과정을 요약하면 아래와 같다.

• mini-batch number $t$에 대하여,
• $X^{\{t\}}$의 값을 구한 후,
• $Z^{[l]}$에 batch norm.을 적용하여 $\tilde Z^{[l]}$을 구한 후, $Z^{[l]}$ 대신 $\tilde Z^{[l]}$ 을 적용한다.
• 그리고 back propagation을 통해 $dW^{[l]}, d\beta^{[l]},d\gamma^{[l]}$ 을 구한다.
• 그리고 gradient descent alg.을 적용하여 $W^{[l]},\beta^{[l]},\gamma^{[l]}$ 값을 갱신한다. (이때, momentum, RMSprop, Adam 등의 optimizer를 사용할 수도 있다.)
  

---

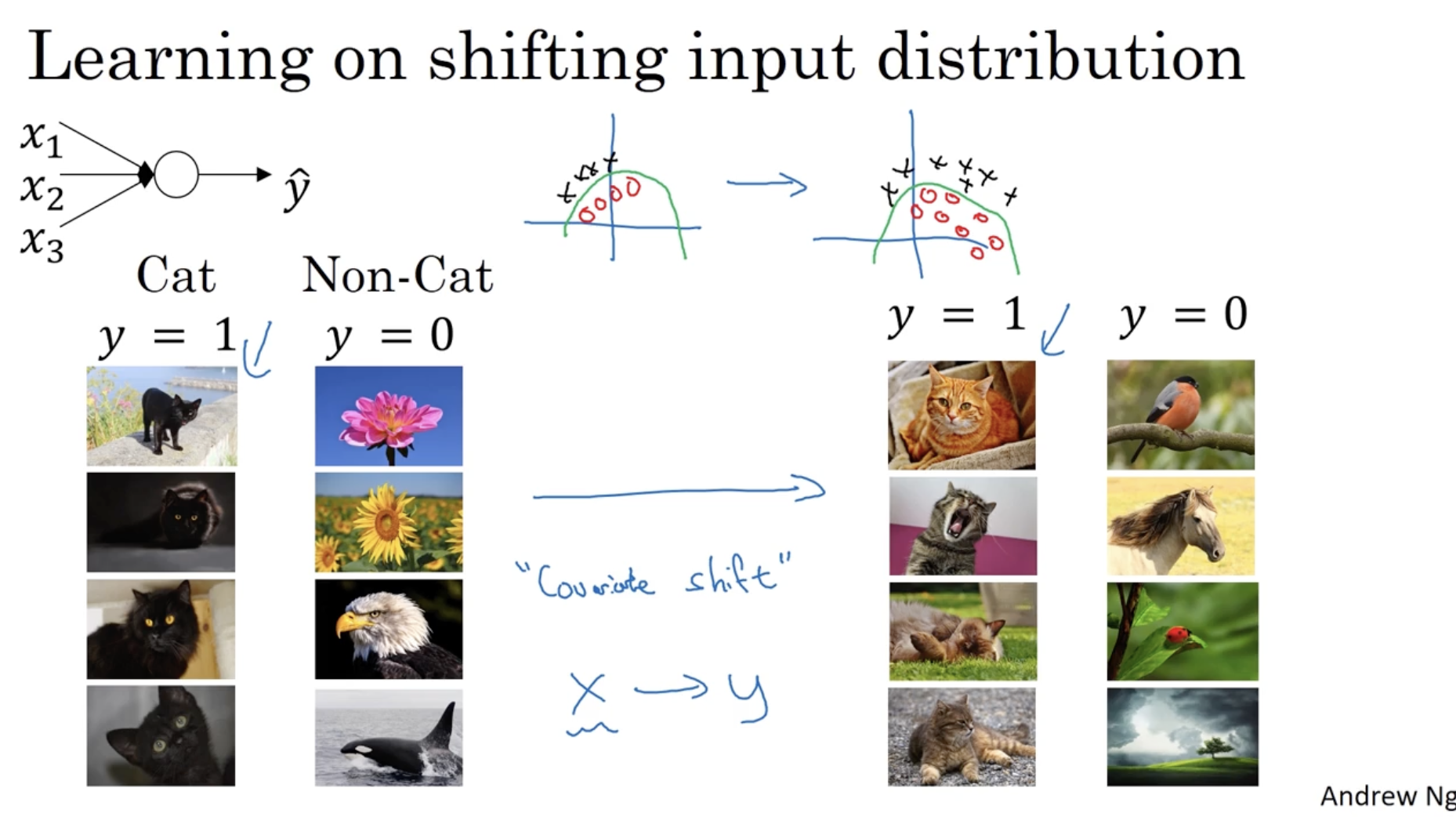
batch normalization 이 효과적인 이유는 무엇일까? 아래 그림을 보자.

• 현재 모델은 좌측 데이터 즉, 검은 고양이 대해서만 인지하는 모델로 학습되었다고 가정해보자.
• 이 경우 유사한데 새로운 데이터 즉, 우측과 같이 유색 고양이 데이터가 주어졌을 때, 이 모델은 기존의 학습된 파라미터에서 또 새롭게 학습을 진행해야 한다.
• 하지만 두 데이터 모두 색의 차이만 존재하고 나머지는 거의 비슷한 feature를 갖는다.
• 따라서 covariate shift 를 적용하면 색만 바뀌고 나머지는 그대로 유지할 수 있다.
• 즉, 데이터를 normalization 하여 동일한 $\mu, \sigma^2$ 값을 갖도록 만들면 아래와 같은 문제를 해결할 수 있다.
• 아래 그래프는 데이터의 평균과 분산은 유지된 상태로 covariate shift를 적용하는 것을 보여준다.
  

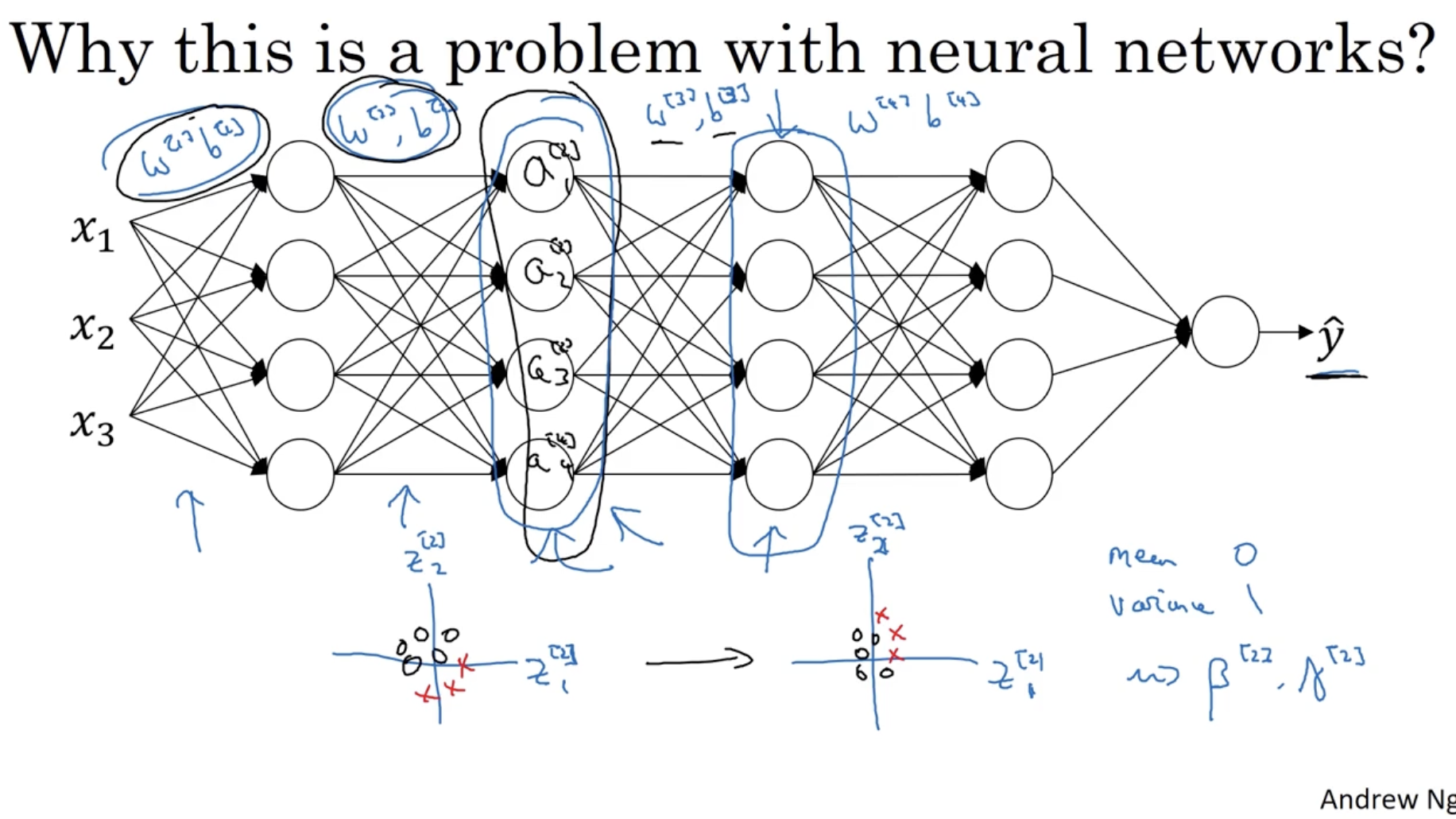
그리고 뉴럴넷의 경우, 이전의 유닛 $a^{[l]}$ 값을 기준으로 현재 파라미터 $W^{[l]},b^{[l]}$를 적용한다. 따라서 그 전의 파라미터들 $W^{[l-1]},W^{[l-2]},...$ 등의 값이 변할 경우, $a^{[l]}$ 값 역시 바뀔 것이다.

• 따라서 히든 레이어 $l$은 레이어 $l-1$의 값만 알 수밖에 없다.
• 하지만 앞서 본 고양이 흑색/유색 데이터에 따른 파라미터는 초반에만 색에 대해서 조정되고 deep 한 쪽의 레이어의 파라미터에는 거의 변화가 없어야 한다.
• 따라서 batch normalization을 적용하여 데이터의 평균과 분산을 유지하는 covariate shift 가 필요하다. 이 경우 평균과 분산은 $\beta, \gamma$ 값에 의해서 결정된다.
• 정리하면 batch normalization을 적용하면 초반 parameter 들의 변화가 있어도 후반 parameter는 그대로 적용되어도 괜찮다는 장점이 있다.
  

또한 batch norm.을 적용할 경우, 평균과 분산에 따라 데이터에 noise가 발생한다.

• 그리고 이는 마치 dropout처럼 각 히든레이어의 activations에 노이즈를 추가한다.
• 따라서 batch norm.은 regularization 측면에서도 (약간의) 장점이 있다.
  

---

테스트 시에 적용되는 batch norm.은 다음과 같다.

• $\mu, \sigma$는 exponentially weighted averages 를 활용하여 구한다.
• 즉, 각각의 mini-batch에서 각 parameter $\mu^{\{1\}[l]},\mu^{\{2\}[l]},...$의 평균값을 exponentially weighted averages를 적용하여 $\mu$를 구한다. ($\sigma$ 도 마찬가지다.)
• 그러고 나서 $z_{norm}=\frac{z-\mu}{\sqrt{\sigma^2+\epsilon}}, \tilde z=\gamma z_{norm}+\beta$ 를 적용하면 된다.
  

---

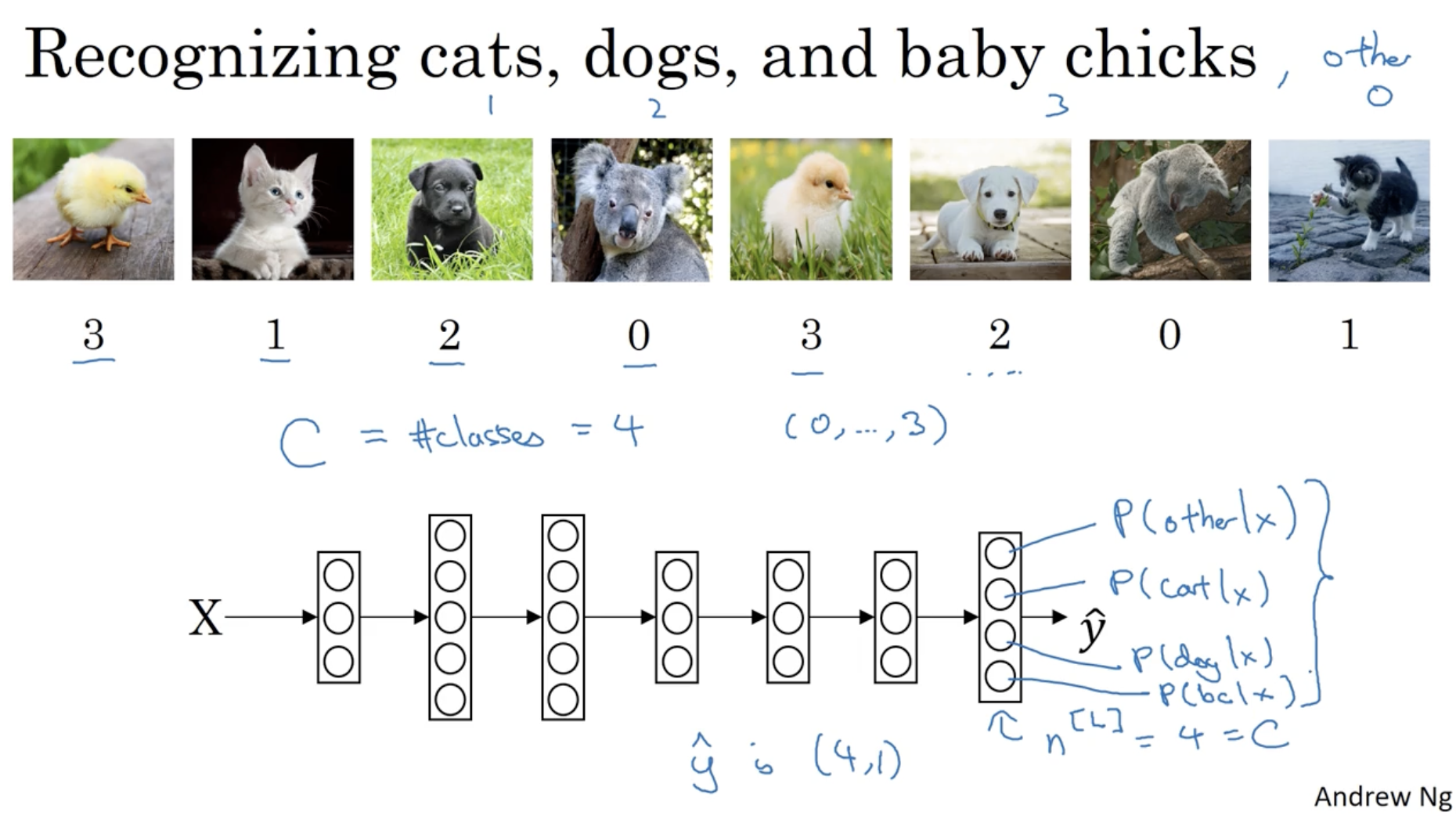
다음으로 multi-classification에 대해서 알아보자. 아래 예시에서 총 4개의 클래스가 있다. (고양이, 개, 병아리, 미포함)

• $C$는 클래스 수를 의미한다. ($C=4$ -> (0, 1, 2, 3))
• 그리고 입력 데이터 $X$를 넣었을 때, 뉴럴넷의 최종 레이어의 아웃풋은 $\hat y \in(4, 1)$으로 나올 것이다.
• 그리고 여기에 softmax function을 적용하여 각각의 클래스에 대한 확률값을 구한다.
  

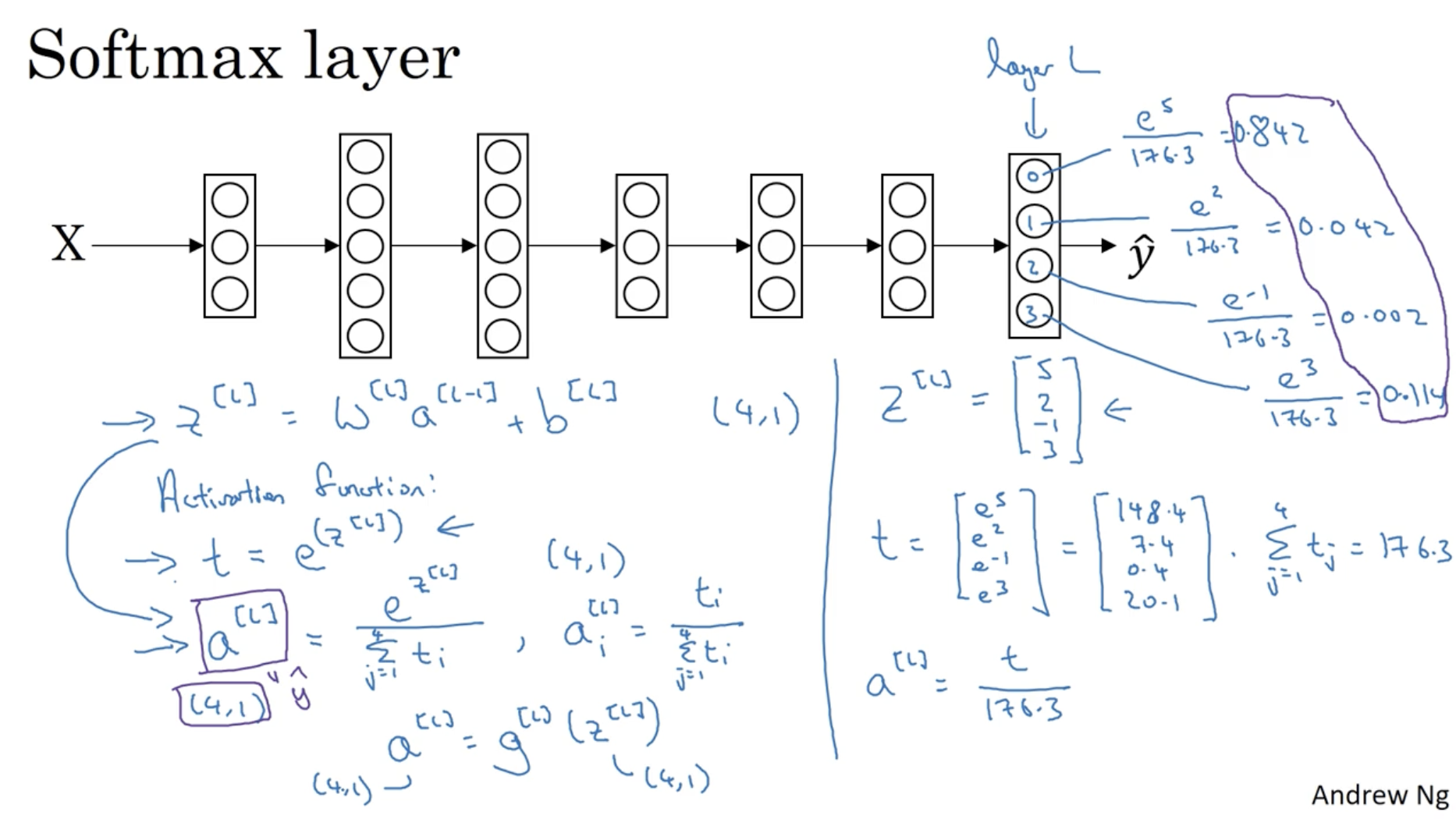
softmax function은 다음과 같다.

• 예를 들어, $z^{[L]}=\begin{bmatrix}5 \\ 2 \\ -1 \\ 3\end{bmatrix}$으로 나왔다면,
• $t=\begin{bmatrix}e^5 \\ e^2 \\ e^{-1} \\ e^3\end{bmatrix}$으로 나올 것이고,
• $\sum_{i=1}^4t_i=176.3$으로 나온다.
• 따라서 각각의 클래스에 대한 확률 $a^{[L]}$은 다음과 같이 나온다. $\hat y =a^{[L]}=\begin{bmatrix}\frac{e^5}{176.3} \\ \frac{e^2}{176.3} \\ \frac{e^{-1}}{176.3} \\ \frac{e^3}{176.3} \\ \end{bmatrix}$
• 따라서 확률값이 가장 높은 $\frac{e^2}{176.3}$에 해당하는 클래스로 분류를 할 수 있다.
• 그리고 중요한 게 있는데 softmax를 적용하기 전에, $a^{[L]}=g^{[L]}(z^{[L]})$과 같은 수식을 적용하여, $e^{value}$에서 value의 값이 작아지도록 만들어줘야 한다. (ex. sigmoid -> 0~1 사이의 값)
  

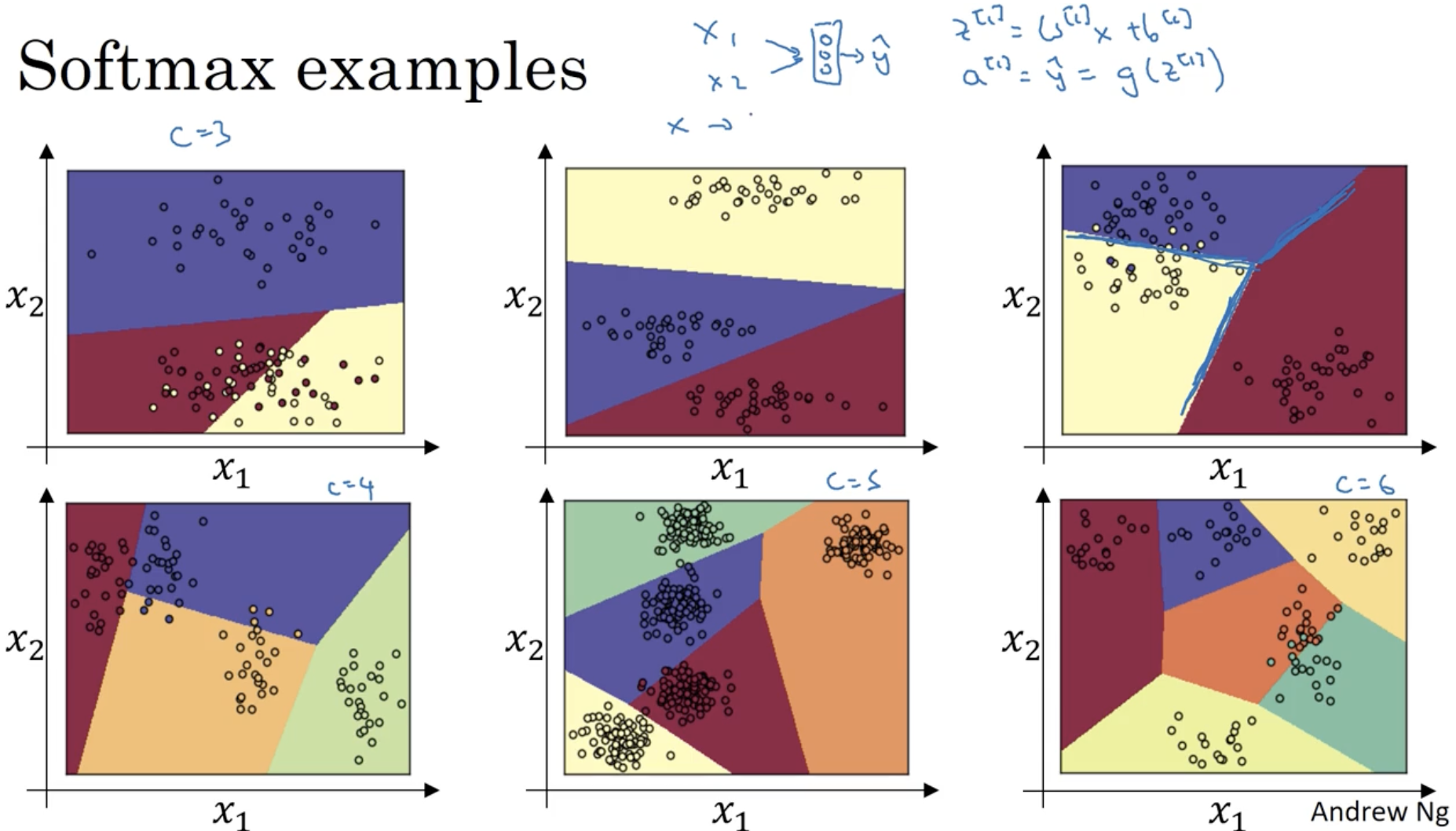
아래는 softmax에 대한 예시들이다. 클래스 차원이 높아질수록 뉴럴넷의 구조는 더 deep해질 것이다.

---

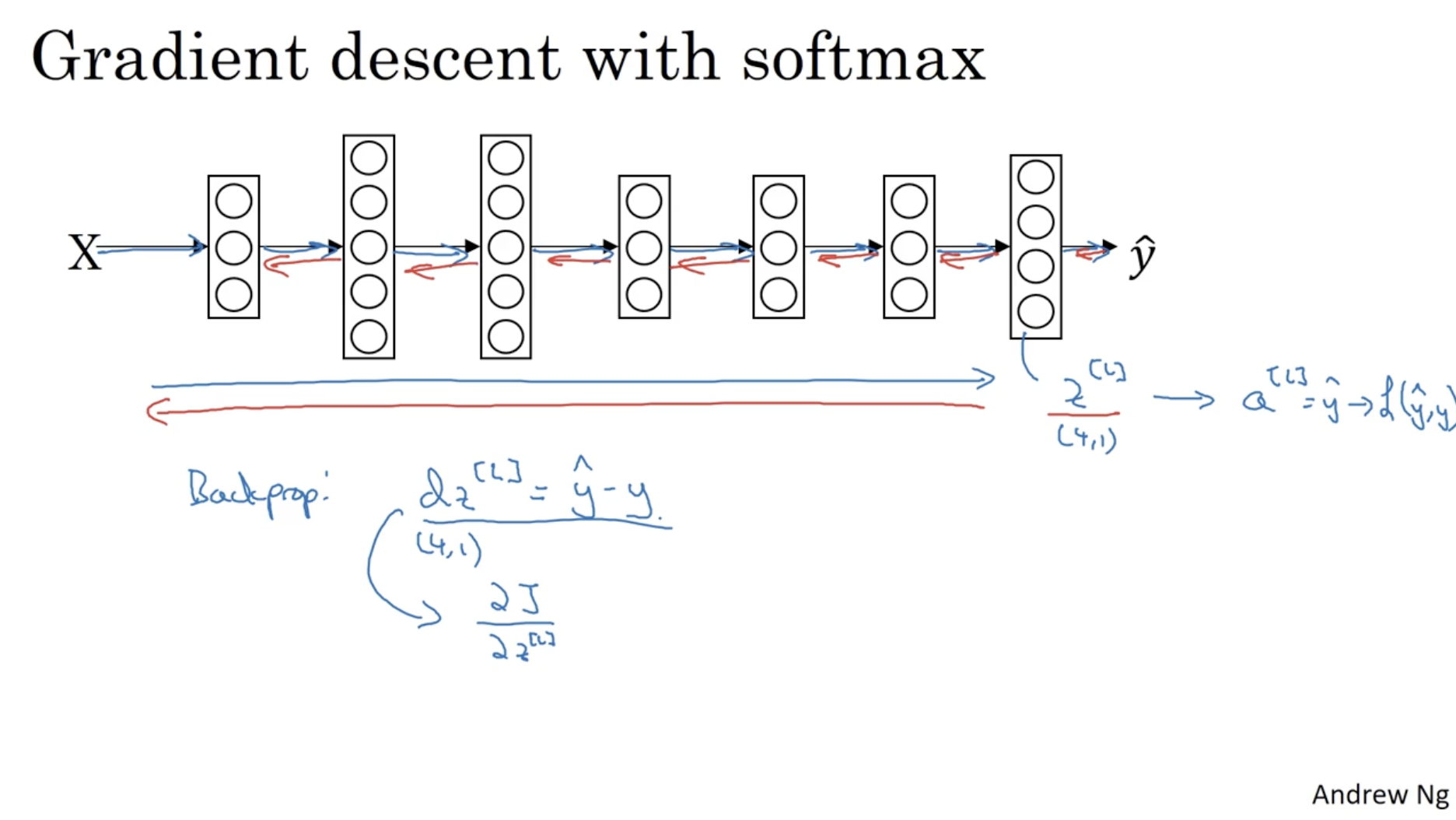
softmax에 대한 loss function은 아래와 같다.

• 예를 들어, $y^{(1)}=\begin{bmatrix}0 \\ 1 \\ 0 \\ 0\end{bmatrix}$라고 가정해보자. (즉 고양이인 경우이다. $y_2=1,y_0=y_1=y_3=0$)
• 이 경우 Loss function은 다음과 같이 나온다. $L(\hat y, y)=-\sum_{j=1}^{4}y_jlog \hat y_j=-y_2log\hat y_2=-log\hat y_2$
• 따라서 $y_2$인지 아닌지를 (고양이인지 아닌지) 잘 학습할 것이다.
• 그리고 $m$개의 데이터에 대해서 Cost function을 구하면 다음과 같다. $J(W^{[1]},b^{[1]},...)=\frac{1}{m}\sum_{i=1}^m L(\hat y^{(i)}, y^{(i)})$
  

그리고 softmax도 마찬가지로 크게 다를 것 없이 backprop. 을 통해 미분값을 구하여 gradient descent를 적용하여 학습을 한다.