[딥러닝] Convolutional Neural Networks Week 4

출처 : https://www.coursera.org/specializations/deep-learning

다음 face verification 과 face recognition 의 차이를 정리한 내용이다.

• Verification 은 1 : 1 problem 으로도 불리는데, 이는 이미지와 이름/ID 정보가 주어졌을 때, 해당 이미지가 이름/ID 와 매칭되는지 판단하는 것이다.
• Recognition 은 K 명의 사람에 대한 데이터베이스를 가지고 있을 때, 어떤 이미지가 입력으로 주어졌을 때 해당 이미지에 대해서 K 명의 사람들 중 누구에 해당하는지 혹은 해당되지 않는지를 판단하는 것이다.
• 보통 Verification 이 Recognition 보다 더 간단하다. (쉽게 생각해서, verification 은 1:1 로 진행하면 되지만, recognition 은 verification 과정을 K:1 만큼 진행해야 한다.)
  

face recognition 을 위해 one-shot learning 방법이 필요하다.

• 이는 정확히 하나의 example 에 대해서 1 : 1로 비교하는 것을 의미한다. (예를 들어, 어느 회사에 신입 사원이 입사했는데, 이 사원에 대한 얼굴 인식을 진행할 때, 이 사원의 ID 카드에 등록된 이미지 하나만으로 얼굴 인식을 해야 한다.)
• 따라서 아래와 같이 좌측 4개의 인물 데이터베이스에 대하여 새로운 2개의 이미지가 주어졌을 때, 데이터베이스에 있는 이미지 중 동일한 인물을 찾는다.
• 만약 동일 인물이 없다면 매칭하지 않는다.
• 이를 일반적인 딥러닝 모델로 적용하지 않는 이유는 다음과 같다. 예를 들어, 신입 사원이 들어올 때마다 뉴럴넷의 구조 중 마지막에 softmax 를 +1 씩 계속해서 수정할 수 없기 때문이다.
• 따라서 One shot learning 방법이 필요하다.
  

one-shot learning 은 직관적으로 해석하면 다음과 같다.

• 어떤 두 개의 이미지 img1, img2 에 대해서 두 이미지 간의 차이 정도를 계산하면 된다.
• 그래서 만약 두 이미지 간의 차이값이 $\tau$ (threshold) 보다 작거나 같으면 이는 동일한 인물로 예측할 수 있다. (반대의 경우에는 다른 인물로 예측한다.)
  

---

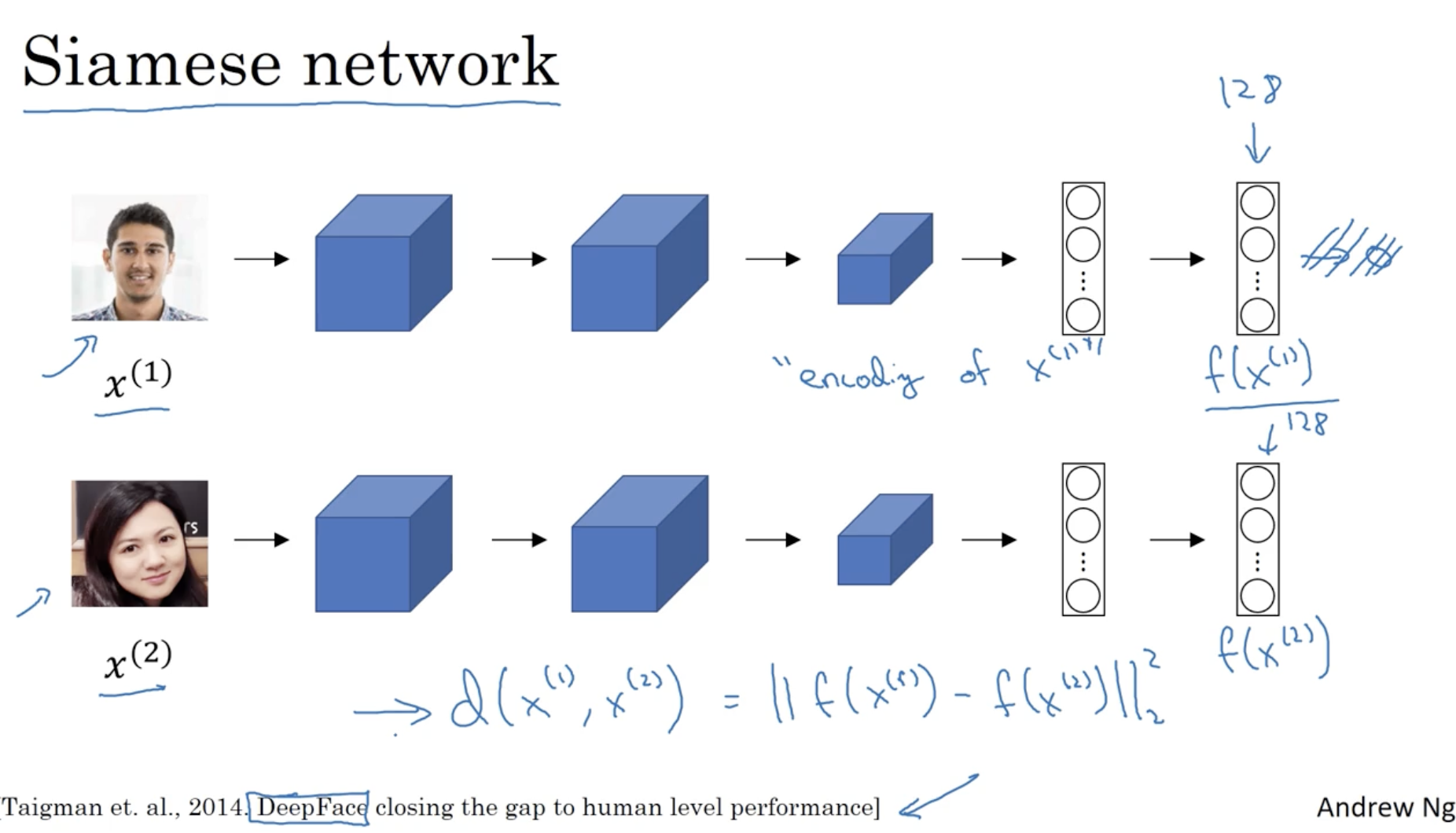
one-shot learning 을 위한 neural net.은 다음과 같다.

• 동일한 모델에 대해서 서로 다른 이미지 데이터 $x^{(1)}, x^{(2)}$ 를 적용한다.
• (이 모델의 경우, softmax layer 는 존재하지 않는다.) 그리고 각각의 마지막 FC layer 즉, $x^{(1)},x^{(2)}$가 인코딩된 값인 $f(x^{(1)}), f(x^{(2)})$ 벡터를 비교하여 두 입력 이미지 간의 차이를 학습한다.
  $d(x^{(1)}, x^{(2)})={||f(x^{(1)}, f^{(2)})||}_2^2$
• 이를 Siamese network 라고 한다.
  

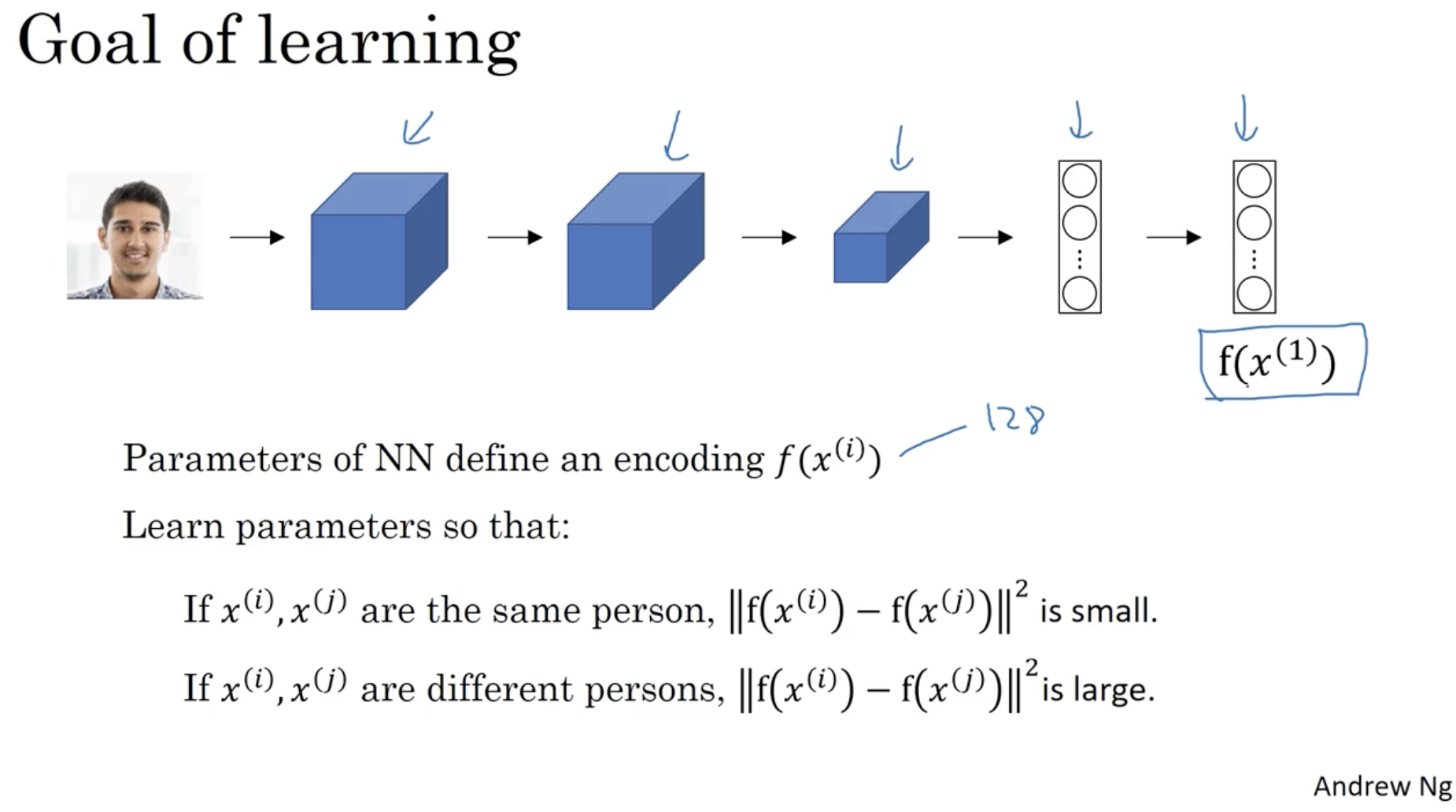
따라서 Siamese network 의 학습 목표는 다음과 같다.

• 만약 $x^{(i)},x^{(j)}$ 가 동일 인물이라면, $d(x^{(i)}, x^{(j)})={||f(x^{(i)}, f^{(j)})||}_2^2$ 값은 작아져야 하며,
• 만약 $x^{(i)},x^{(j)}$ 가 다른 인물이라면, $d(x^{(i)}, x^{(j)})={||f(x^{(i)}, f^{(j)})||}_2^2$ 값은 커져야 한다.
  

---

그렇다면 object function 을 어떻게 정의할 수 있을까? 아래를 보자.

• one-shot learning 을 위해 triplet loss 가 필요하다. 이는 아래와 같이 ( Anchor , Positive , Negative ) 로 총 3개의 데이터에 대해서 Loss 를 구하는 것이다.
• 따라서 다음과 같은 2개의 차이값이 나온다.
  • $d(A,P)={||f(A),f(P)||}_2^2$,
  • $d(A,N)={||f(A),f(N)||}_2^2$
• 그리고 우리는 $d(A,P)\le d(A,N)$ 이 되는 것을 원한다.
  따라서 ${||f(A),f(P)||}_2^2 - {||f(A),f(N)||}_2^2 \le 0$ 가 되기를 원할 것이다.
• 하지만 이 경우 모델이 단순히 $f(x)=0$ 형태로 출력해도 위 조건이 만족된다. 따라서 이를 방지하기 위해 margin 을 더해줘야 한다.
• 따라서 최종적인 수식은 다음과 같이 나온다.
  ${||f(A),f(P)||}_2^2 - {||f(A),f(N)||}_2^2 + \alpha \le 0$
  

따라서 triplet 데이터에 대한 loss function 은 아래와 같다.

• $A, P, N$ 이라는 triplet 학습 data 에 대해서,
• 하나의 triplet 데이터셋에 대한 Loss function 은 다음과 같다.
  $L(A,P,N)=max({||f(A),f(P)||}_2^2 - {||f(A),f(N)||}_2^2+\alpha,0)$
• 따라서 전체 모델의 cost function 은 다음과 같이 나온다.
  $J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})$
• 그리고 모델을 학습할 때, 동일 인물 이미지가 여러 명 있어야 학습이 잘된다.
  

다음으로 triplet 데이터를 어떤 식으로 선택하면 좋을지에 대한 내용이다.

• 만약 랜덤하게 A, P, N 을 선택하면 어떻게 될까? 이 경우, 일반적으로 사람들 간의 얼굴 차이가 더 크게 나타날 수밖에 없을 것이다. 따라서 loss 의 조건이 금방 만족되어 학습이 금방 끝날 것이다.
• 따라서 hard 한 방식으로 $d(A,P)\approx d(A,N)$ 인 데이터를 뽑아서 학습해야 한다.
  

---

다음으로 neural style transfer 에 대해서 알아본다.

• 아래와 같이 content C와 style S 이미지 데이터를 합쳐서 새로운 이미지 데이터 generated image G 를 생성하는 방법이다.
  

---

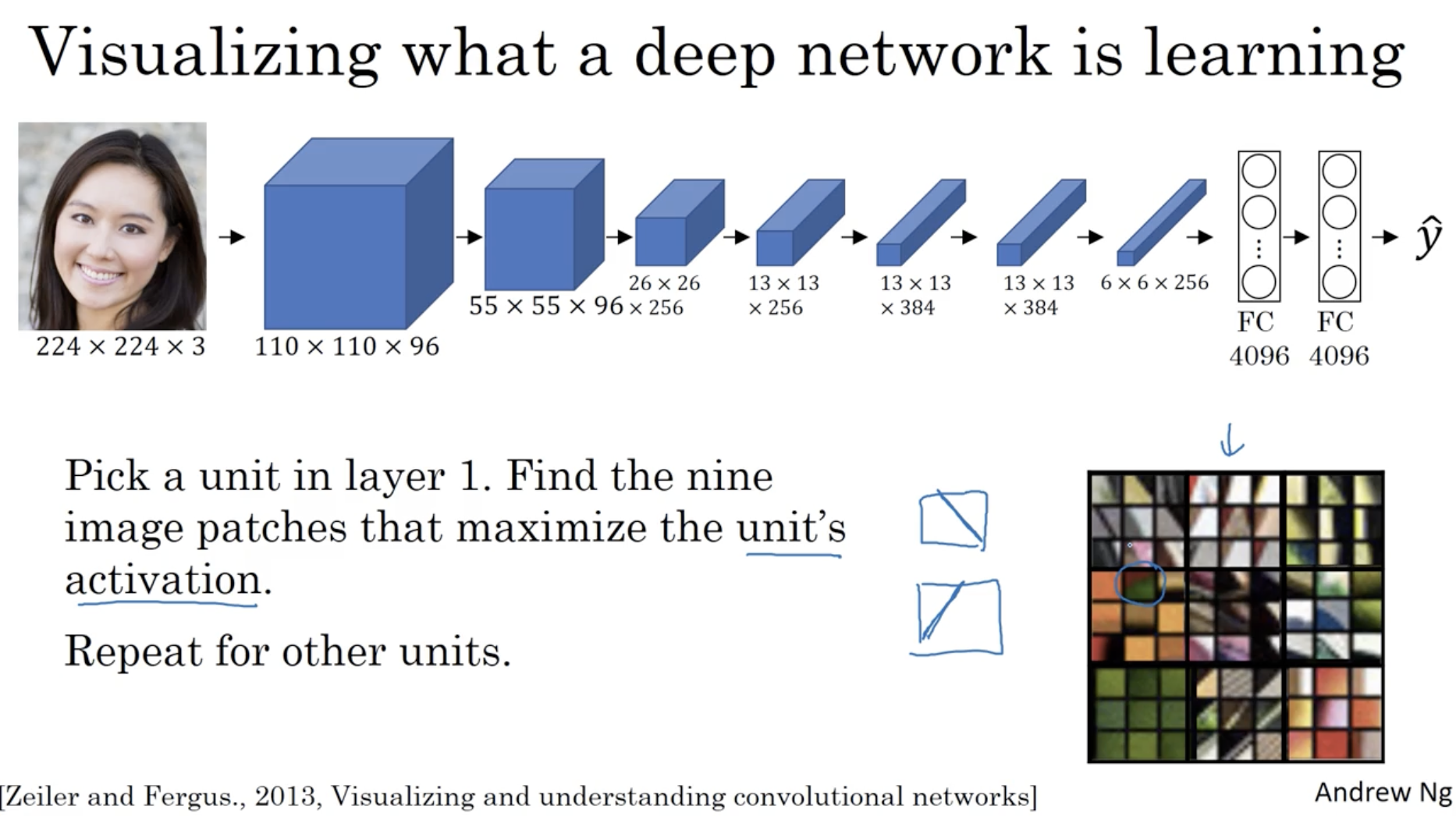
우선 deep neuron network 에서 어떤 식으로 학습이 되어가는지를 시각화하면 아래와 같다.

• 아래 예시는 layer 1 에 대한 activation 값이 최대가 되는 9개의 이미지 패치를 각각의 hidden unit 에 대해서 추출하여 시각화한 예시이다.
• 우측 아래와 같이 총 9개의 image patch 를 추출하였고, 좌측 상단에 해당하는 hidden unit 은 edge 와 같은 feature 를 학습하고 있고, 4번째 해당하는 hidden unit은 오렌지색 컬러 feature 를 주로 학습하고 있는 것 같다.
• 이처럼 layer 1의 각각의 hidden unit 들이 주로 학습하고 있는 feature 를 시각화하였다.
  

그리고 각 layer 마다 비교할 경우 아래와 같은 image patches 들이 나온다.

• 초반에는 hidden unit 들이 edge 와 같은 단순한 패턴을 학습했다면, deep 해질수록 복잡하고 정교한 패턴을 학습하는 것을 확인할 수 있다.
  

---

neural style transfer 의 cost function 다음과 같다.

• $J(G)=\alpha J_{Content}(C,G)+\beta J_{Style}(S,G)$
• 즉, content 이미지 C와 style 이미지 S에 대해서 각각의 가중치 $\alpha, \beta$ 에 따라 유사해지도록 만드는 것이다.
  

따라서 다음과 같은 절차로 학습할 수가 있다.

• 먼저 초기 G image 를 랜덤하게 초기화한다.
• 그러고 나서 cost function $J(G)=\alpha J_{Content}(C,G)+\beta J_{Style}(S,G)$ 를 활용하여 학습을 한다.
• 우측과 같이 초기 generated image 는 학습을 거치면서 점점 content 이미지와 style 이미지와 유사해지는 것을 확인할 수 있을 것이다.
  

---

content cost function은 아래와 같다.

• (not shallow and not deep) hidden layer $l$ 에 대해서 content cost 를 계산한다.
• 미리 학습된 ConvNet (ex. VGG network) 을 사용한다.
• generated image G와 content image C에 대해서 각각 $l$ 번째 히든 레이어에서의 activation 값 $a^{[l](C)}, a^{[l](G)}$ 를 구한다.
• cost function $J_{Content}(C,G)={||a^{[l](C)} - a^{[l](G)}||}_2^2$ 를 통해서 content image와 generated image 간의 유사도를 판단한다.
  

---

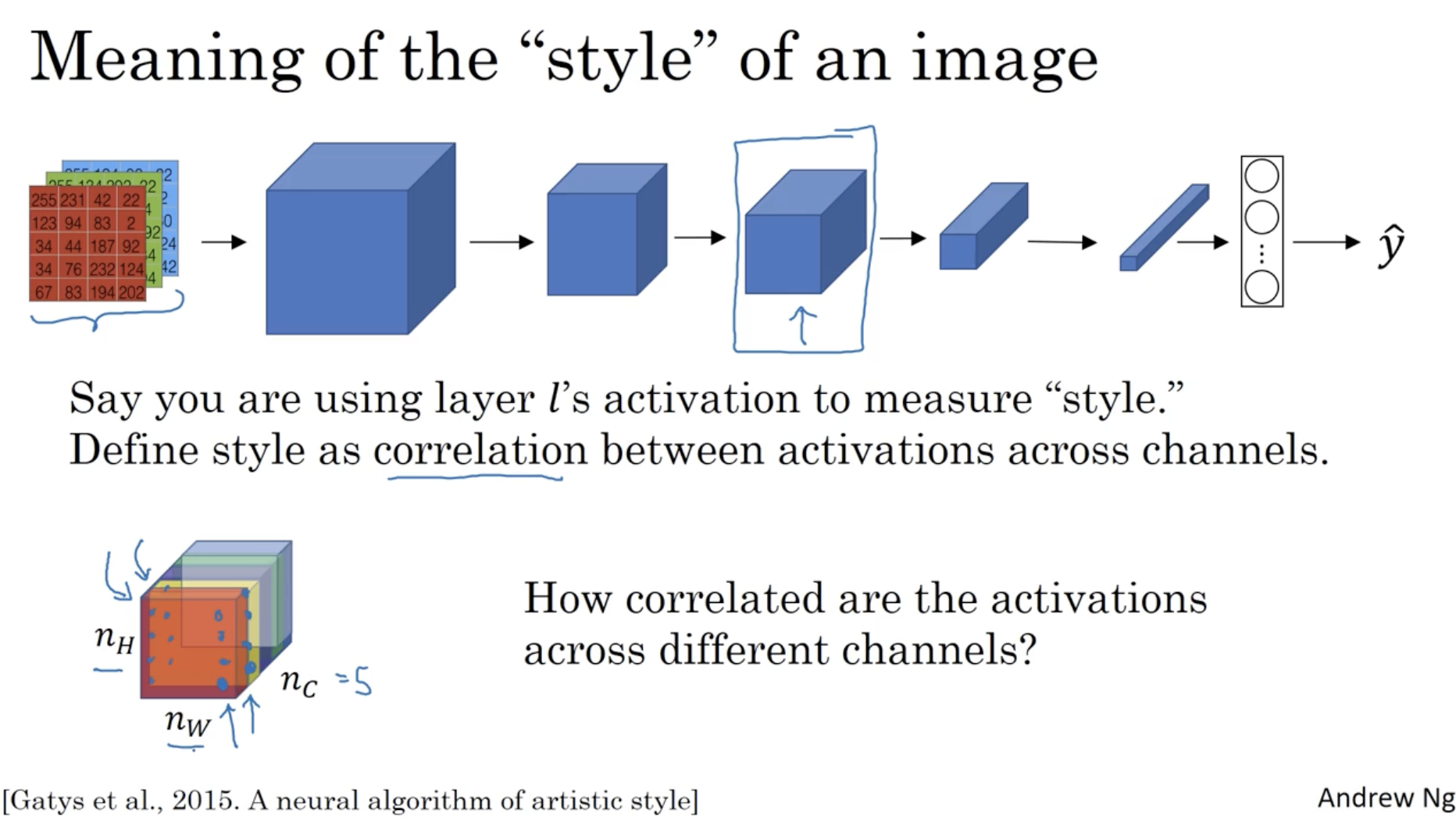
다음으로 style cost function을 알아보자.

• style 이 유사하다는 것은 어떤 의미인지부터 파악한다.
• 이는 activations의 채널 간의 correlation 유사하면 style이 유사하다고 판단할 수 있다.
• 예를 들어 아래에서 빨간색 채널과 노란색 채널이 있을 때, 각각의 ($w,h$) 좌표에 맞춰 두 채널 간의 correlation 정도를 판단한다.
  

구체적인 예시는 아래와 같다.

• 좌측 style image의 빨간색 채널과 노란색 채널의 correlation 정도를 확인해보자.
• 빨간색 채널의 경우 vertical pattern 을 학습하고 있고, 노란색 채널은 orange color 를 학습하고 있다.
• 따라서 만약 두 채널 간의 correlation 이 높다면, 같은 좌표에서 특정 vertical 패턴이 특정 orange 컬러를 의미해야 한다. (만약 correlation 이 낮다면, vertical 패턴과 orange 컬러는 아무 상관관계가 없을 것이다.)
  

따라서 이를 이를 이용하여 cost function 을 정의할 수 있다.

• 우선 notation 을 정의하자. $a_{i,j,k}^{[l]}$ 은 $l$ 레이어에 있는 $(i,j)$ 좌표의 $k$ 채널에 대한 activation 을 의미한다.
• 그리고 $G^{[l]}$는 Gram matrix 를 의미하며, $n_c^{[l]} \times n_c^{[l]}$의 크기를 갖는다.
• 먼저 style 이미지의 $G^{[l]}$은 다음과 같다.
  • $G^{[l](S)}=\sum_{i=1}^{n^{[l]}_H}\sum_{j=1}^{n^{[l]}_W}a_{i,j,k}^{[l](S)}a_{i,j,k'}^{[l](S)}$ ( $k=1,...,n_c^{[l]}$)
• 다음으로 generated 이미지의 $G^{[l]}$은 다음과 같다.
  • $G^{[l](G)}=\sum_{i=1}^{n^{[l]}_H}\sum_{j=1}^{n^{[l]}_W}a_{i,j,k}^{[l](G)}a_{i,j,k'}^{[l](G)}$ ( $k=1,...,n_c^{[l]}$)
• 따라서 Style cost function 은 다음과 같이 정의한다.
  • $J_{style}^{[l]}(S,G)=\frac{1}{(2\times n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]})^2}{||G^{[l](S)}-G^{[l](G)}||}_F^2$
  • $J_{style}^{[l]}(S,G)=\frac{1}{(2\times n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]})^2}\sum_{k}\sum_{k'}(G_{kk'}^{[l](S)}-G_{kk'}^{[l](G)})^2$
    

따라서 style cost function 은 아래와 같으며, neural transfer learning 의 cost function $J(G)$ 는 다음과 같다.

• $J(G)=\alpha J_{Content}(C,G), \beta J_{Style}(S,G)$
  

---

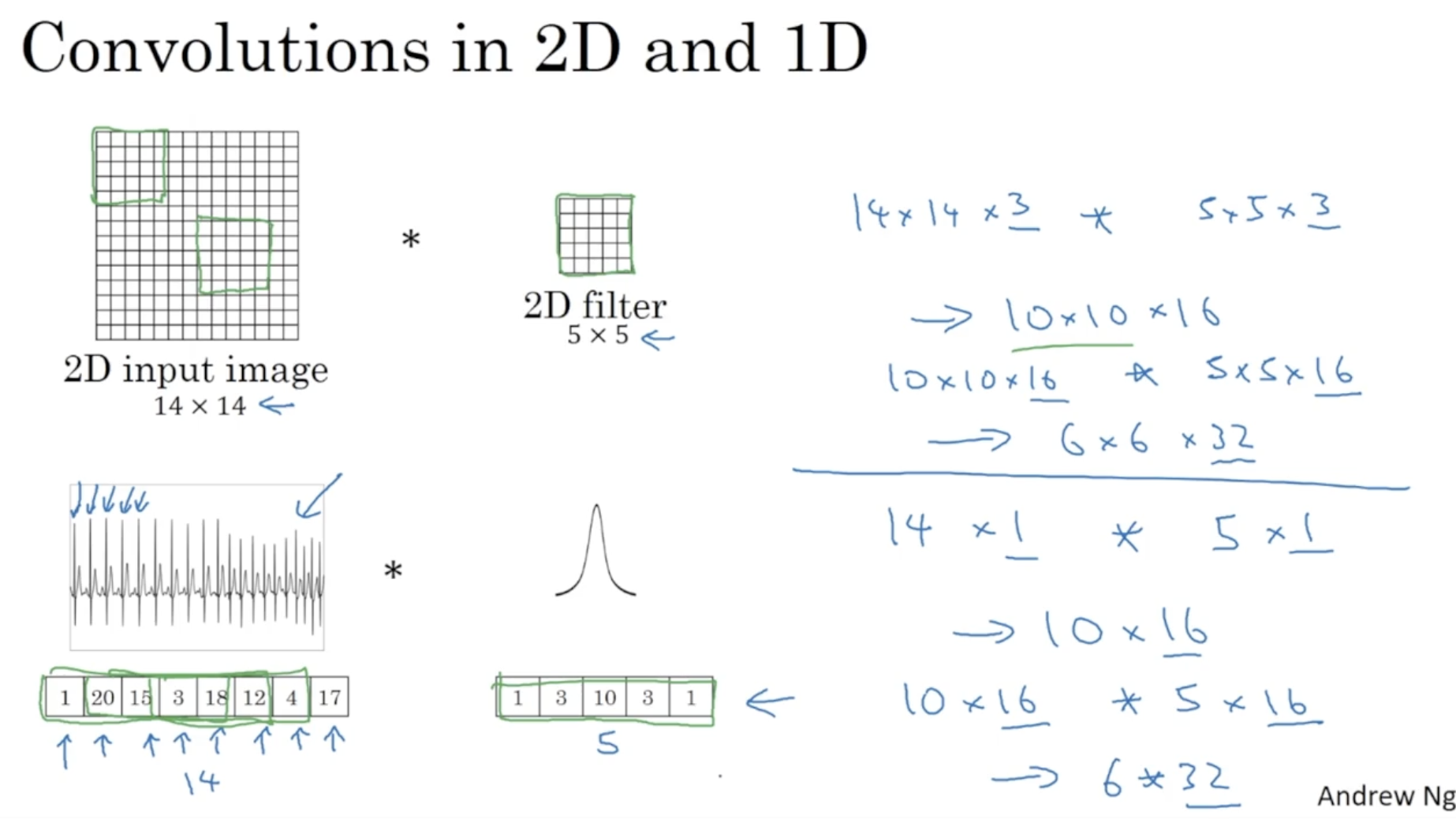
그리고 다음 강의의 예고편으로, 아래와 같이 2D conv. 를 1D conv. 와 3D conv. 로도 적용할 수 있다.