[딥러닝] Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization Week 1

출처 : https://www.coursera.org/specializations/deep-learning

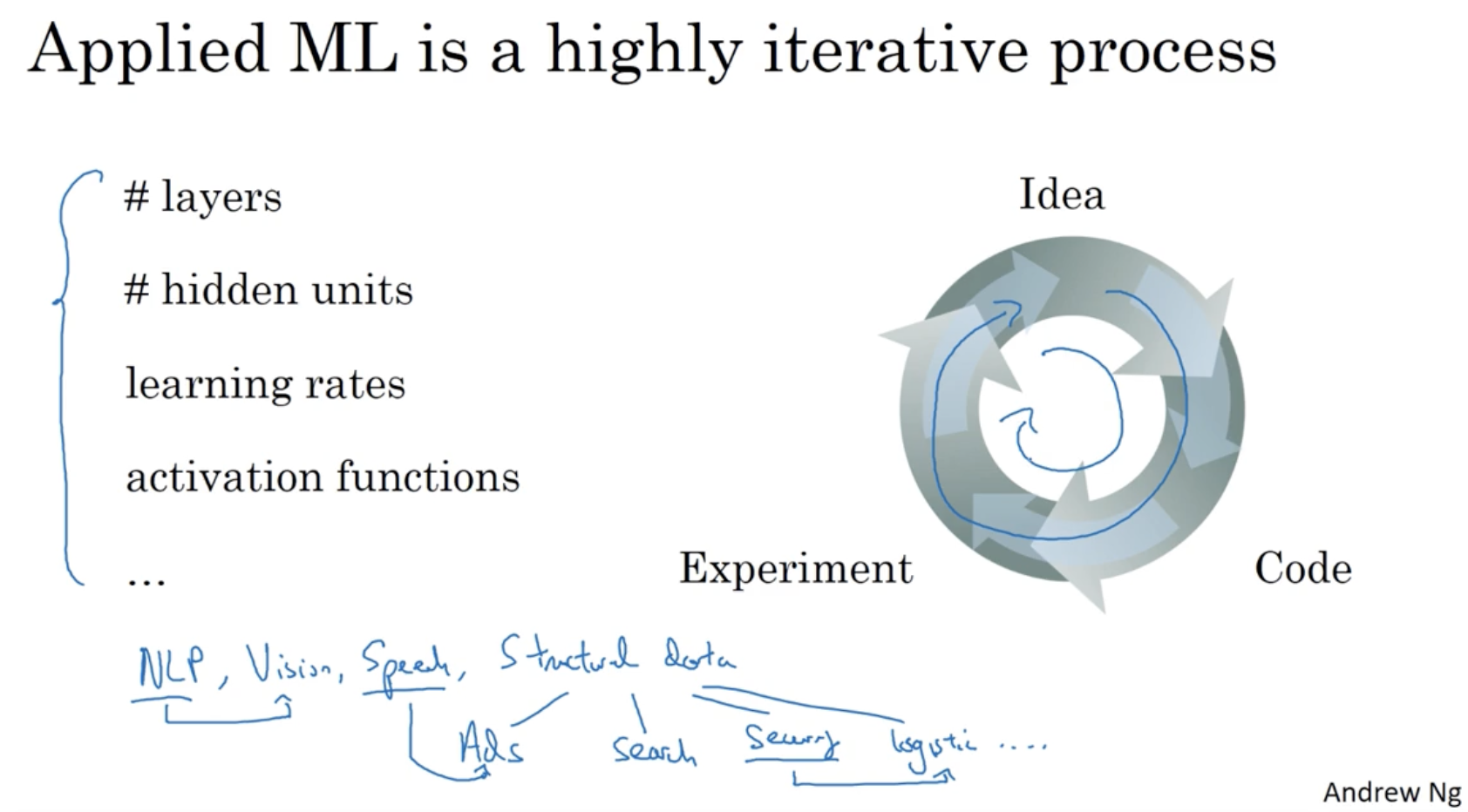
보통 ML을 학습하는 과정은 순환 구조를 이룬다. 아래 그림과 같이 Idea를 Code로 적용하고 Experiment를 통해 결과를 확인하여 새로운 Idea를 적용하고 ... 등의 순환 구조를 이룬다.

• 그리고 Deep NN에서 레이어의 수, 히든 유닛의 수, learning rate, activation function 등의 다양한 하이퍼 파라미터가 존재한다.
  

보통 딥러닝 모델의 데이터를 다음과 같이 나눈다.

• train set : 학습 데이터 / dev set(cross validation set) : 실험 데이터 / test set : 테스트 데이터
• 데이터 수가 1000, 10000 처럼 적을 경우, 데이터를 (train/test, 70%/30%) 혹은 (train/dev/test, 60%/20%/20%)와 같이 나눈다.
• 하지만 데이터 수가 1,000,000처럼 매우 많을 경우, train/dev 99%/1%처럼 거의 train set으로 활용하며, dev나 test는 1% 이하로 적용한다.
  

다만 주의할 점이 train set과 dev(or test) set의 데이터가 같은 종류여야 한다는 것이다.

• 예를 들어 웹페이지에서 고양이 이미지를 가지고 학습한 모델에 휴대폰으로 찍은 고양이 이미지로 dev/test set을 적용하면 이는 부적절하다.
• 그리고 데이터가 많을 경우 test set 없이 dev set만 있어도 괜찮다.
  

다음으로 bias와 variance 개념을 알아보자

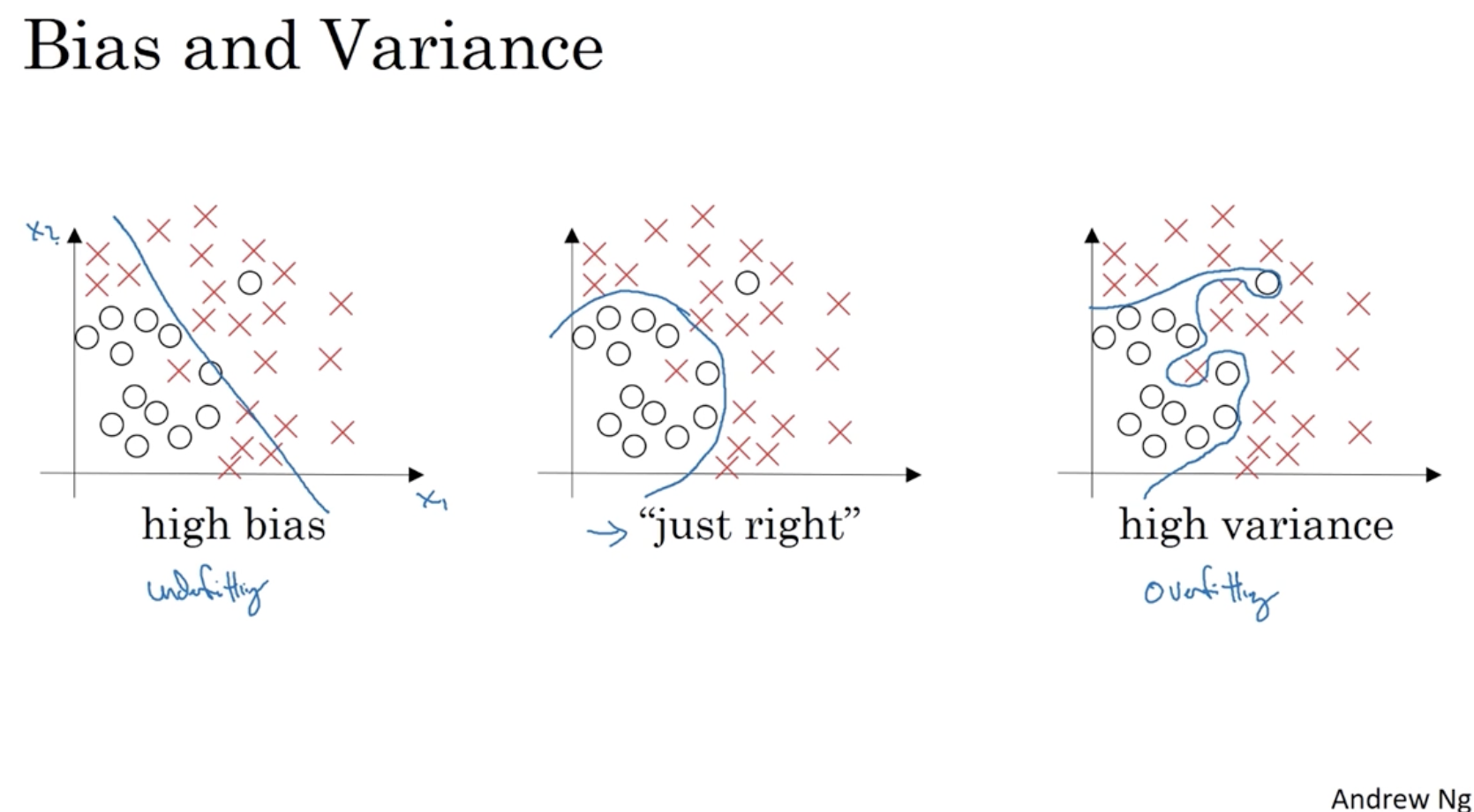
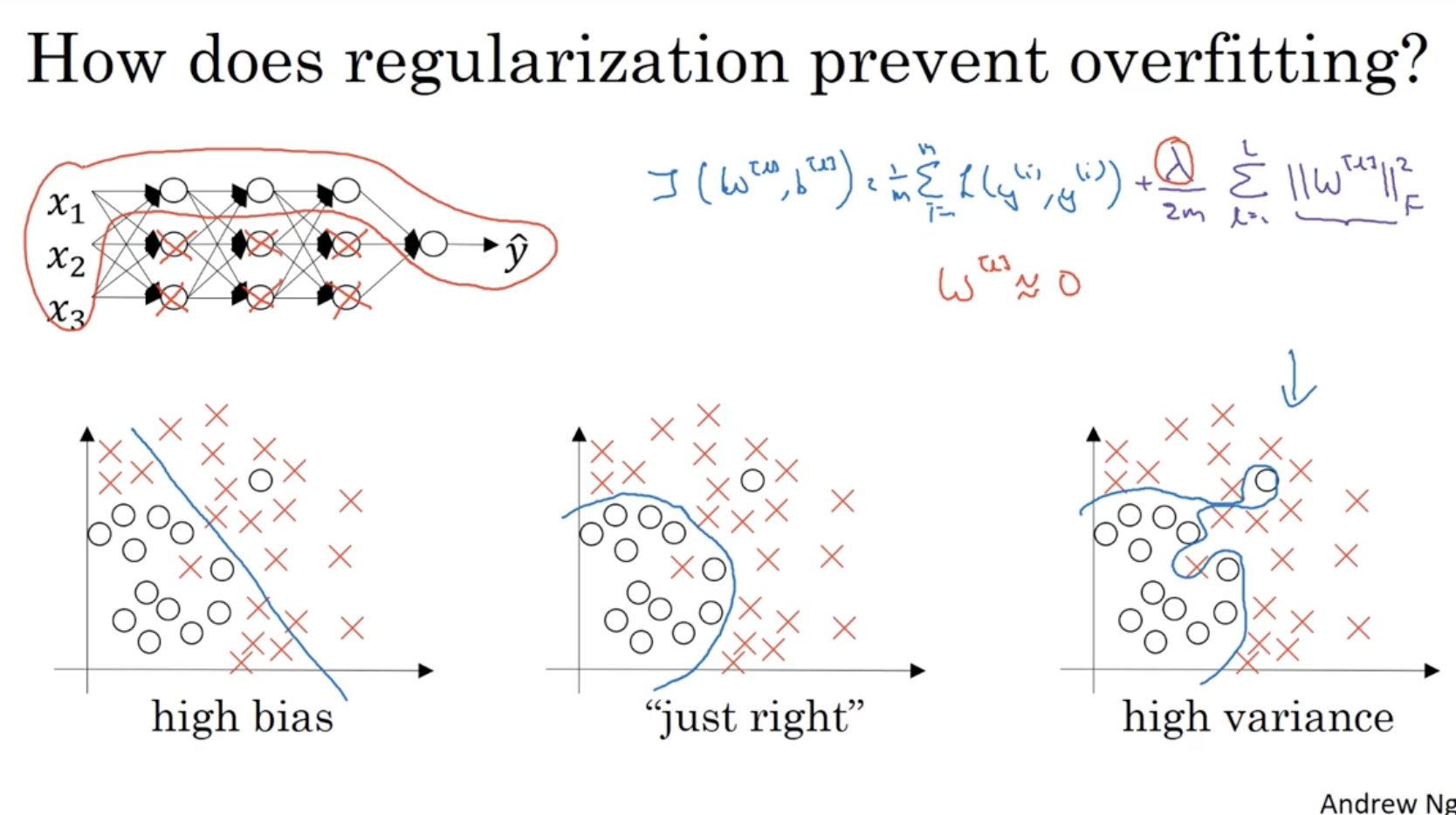
• 아래 그림에서 좌측과 같이 train set에 대해서 높은 error를 보이는 경우를 high bias라고 한다.
• 그리고 우측과 같이 매우 복잡한 함수가 나오는 경우를 high variance라고 한다.
• 따라서 가장 이상적인 모델은 중간에 있는 그래프처럼 train set에 대해서 낮은 에러를 보이며, 함수가 복잡하지 않은 low bias and low variance 모델이다.
  

train set과 dev set의 에러에 따른 bias 및 variance를 분류해보자.

• 모델에 이미지를 입력했을 때 이 이미지가 고양인지 아닌지를 분류하는 모델이라고 가정해보자.
• train set error : 1% \ dev set error : 11%
  • 이 경우 train set에 대해서는 에러가 낮지만, dev set에 대해서는 에러가 높다.
  • 따라서 train set에 맞춰서 복잡한 함수가 만들어진 것으로 보인다.
  • 그러므로 이는 high variance에 해당한다.
• train set error : 15% \ dev set error : 16%
  • 이 경우 train set에 대한 에러와 dev set에 대한 에러가 비슷한 값으로 높게 나왔다.
  • 이는 train set과 dev set 모두 에러가 높게 나오는 high bias를 의미한다.
• train set error : 15% \ dev set error : 30%
  • 이 경우 train set에 대한 에러는 높게 나오고, dev set에 대한 에러는 더 높게 나왔다.
  • 따라서 이는 비교적 train set에 맞춰진 복잡한 함수가 만들어진 것으로 보인다.
  • 그러므로 이는 high bias 및 high variance에 해당한다.
• train set error : 0.5% \ dev set error : 1%
  • train set과 dev set 모두 충분히 낮은 에러가 나왔다.
  • 그러므로 이는 low bias 및 low variance에 해당한다.
• 그리고 에러가 높다/낮다의 기준은 optimal error (bayes error) 를 어떻게 정의하냐에 따라 다르다. 아래의 경우 optimal error가 0에 가까운 값이라 위와 같은 판단을 할 수가 있다.
  

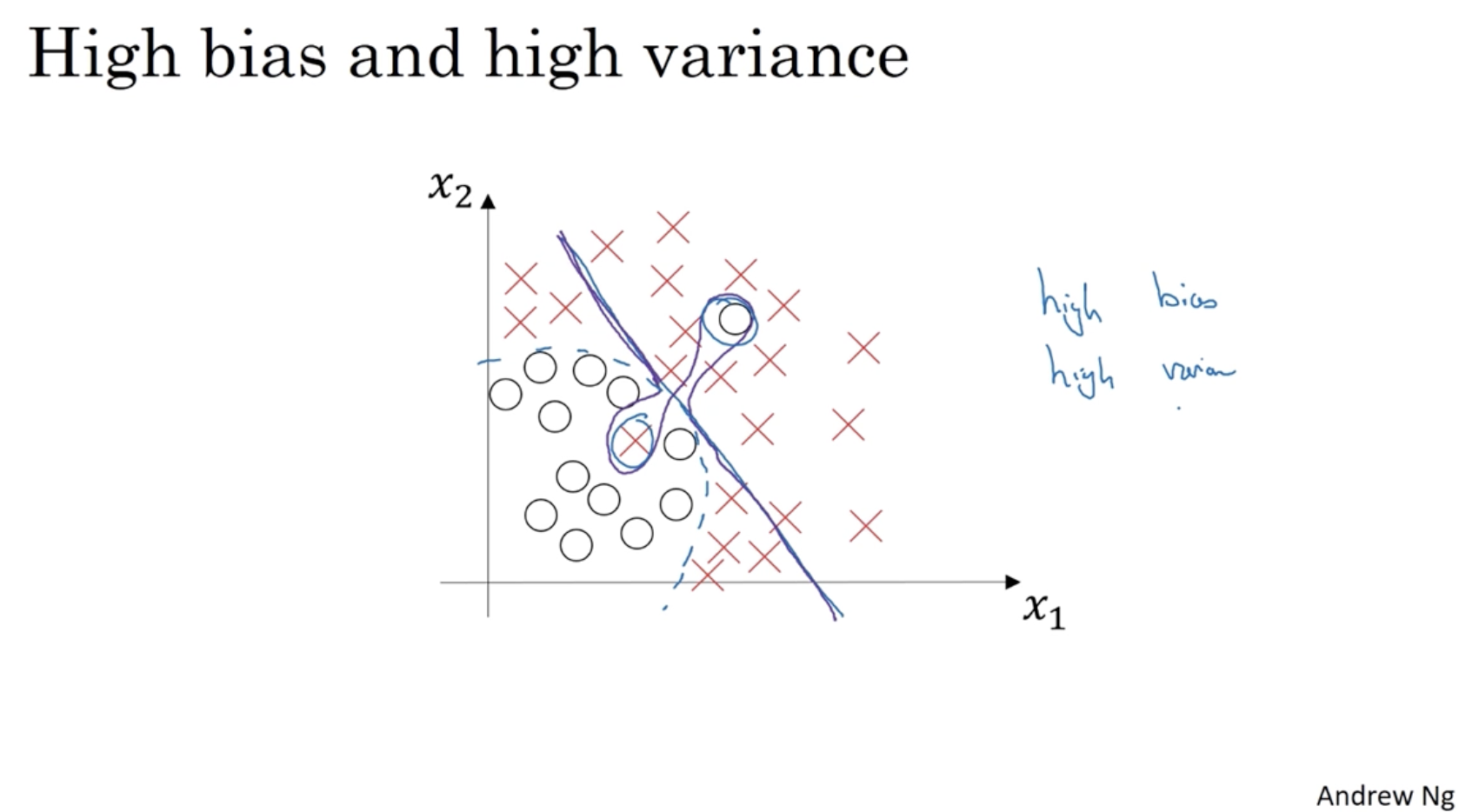
high bias이면서 high variance에 해당하는 그래프는 아래와 같다.

• 매우 복잡한 함수 모양을 가지면서 에러가 높게 나오는 것을 볼 수 있다.
  

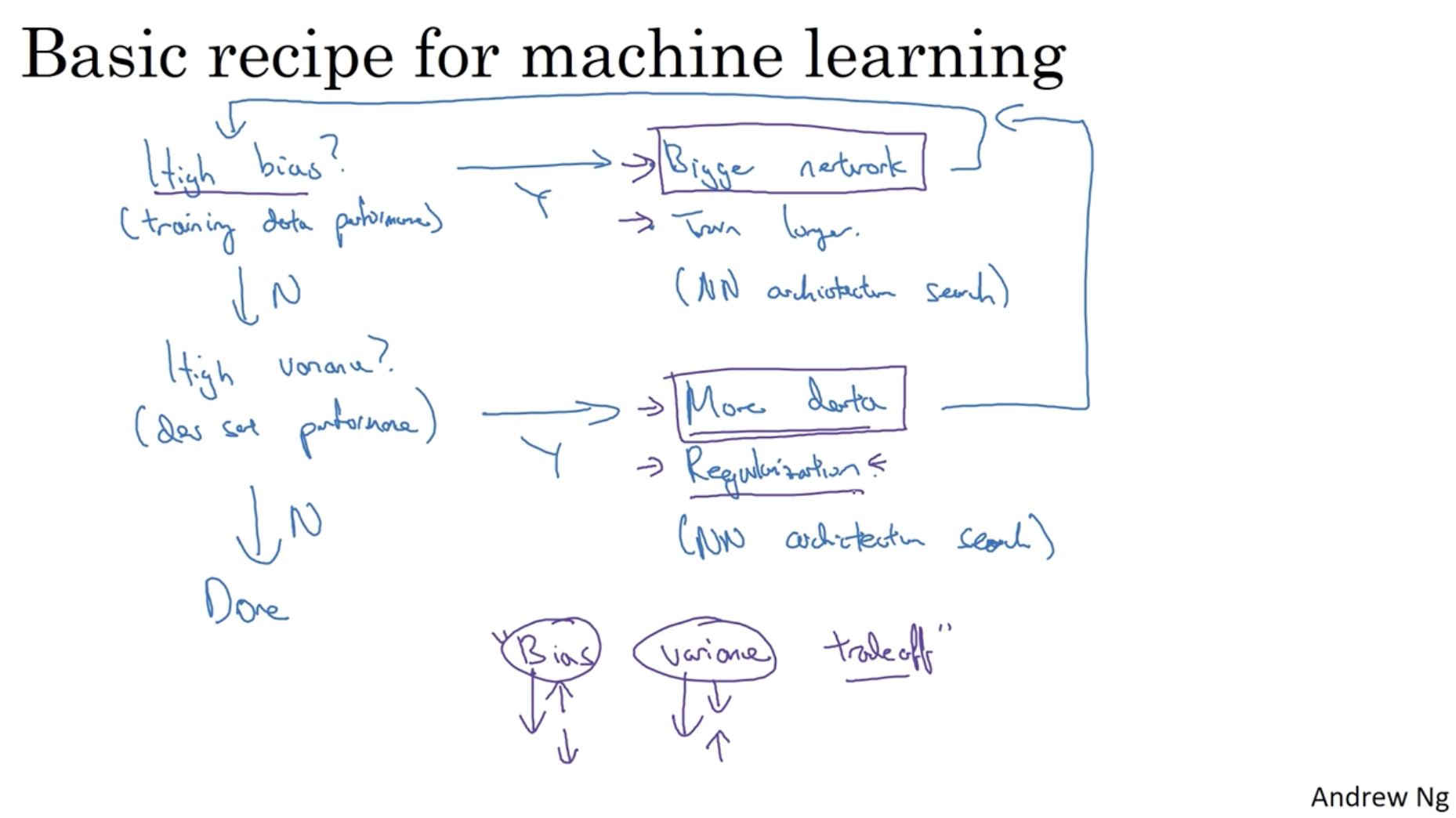
따라서 머신 러닝 모델의 high bias 및 high variance 문제를 해결하려면 아래와 같은 방식으로 적용하면 된다.

• high bias? (to train set)
  • 만약 high bias를 보인다면, network를 더 크게 만들면 된다.
  • 그러고 나서 다시 모델을 돌려서 high bias 인지를 확인한다.
  • 만약 low bias라면 다음 단계인 high variance 여부 단계로 넘어간다.
• high variance? (to dev set)
  • 만약 high variance를 보인다면, 1) 데이터를 더 추가하거나 2) Regularization 을 적용한다.
  • 그러고 나서 다시 모델을 돌리며 high bias 여부 단계로 넘어간다.
  • 만약 low variance라면 해당 모델은 완전한 모델이라고 볼 수 있다.
• 이처럼 bias와 variance는 서로 trade-off 관계에 있다. 이를 잘 조정하는 것이 중요하다.
  

---

이제 regularization에 대해서 알아보자. 우선 Logistic regression에서의 regularization을 알아본다.

• 아래와 같이 regularization이 적용된 cost function은 다음과 같다.
  • L-2 regularization) $J(w,b)=\frac{1}{m}\sum_{i=1}^mL(\hat y^{(i)}, y^{(i)})+\frac{\lambda}{2m}{||w||}_2^2$
  • L-1 regularization) $J(w,b)=\frac{1}{m}\sum_{i=1}^mL(\hat y^{(i)}, y^{(i)})+\frac{\lambda}{2m}{||w||}_1$
• 위에서 $\lambda$는 regularization parameter를 의미한다. (python에서 lambda는 약속어로 되어 있어 "lambd"로 대신 표기한다.)
• 다만 L-1 regularization은 $w$를 sparse하게 만든다는 단점이 있어 보통 L-2 regularization을 적용한다.
  

다음은 Neural Network에 대한 regularization이다.

• L-2 regularization이 적용된 nueral net.의 cost function은 다음과 같다.
  $J(W^{[1]},b^{[1]},...,W^{[L]},b^{[L]})=\frac{1}{m}\sum_{i=1}^mL(\hat y^{(i)},y^{(i)})+\frac{\lambda}{2m}\sum_{l=1}^{L}{||W^{[l]}||}_F^2$
• 위에서 ${||W^{[l]}||}_F^2$ 와 같은 form을 "Frobenius normarization"이라고 한다.
• 그리고 back propgation을 통해 $W$의 미분값을 구한 후 해당 미분값을 가지고 gradient descent alg.을 적용할 수 있다.
  • $dW^{[l]}=(back\ propagation) + \frac{\lambda}{m}W^{[l]}$
  • $W^{[l]}=W^{[l]}-\alpha\ dW^{[l]}$
• 위에서 이전의 $W$의 weight가 줄어든다는 것을 보장하는 방법은 다음과 같다.
  • $W^{[l]}=W^{[l]}-\alpha\ dW^{[l]}$
  • $W^{[l]}=W^{[l]}-\alpha((back\ propagation) + \frac{\lambda}{m}W^{[l]})$
  • $W^{[l]}=W^{[l]}(1-\frac{\alpha\lambda}{m})-\alpha(back\ propagation)$
  • $(1-\frac{\alpha\lambda}{m})$는 무조건 1보다 작기 때문에 이전의 $W^{[l]}$의 비중은 줄어들고 $-\alpha(back\ propagation)$의 영향을 더 많이 받을 것이다.
    

Regularization이 overfitting을 방지하는 직관적인 해석은 다음과 같다.

• 하단 우측 그래프처럼 high variance를 갖는 경우, $W^{[l]}=0$과 같이 적용하면, 좌측 상단의 뉴럴넷처럼 다른 유닛들에 대한 가중치는 0이 되기에, 비교적 단순한 구조의 뉴럴넷이 만들어진다.
• 따라서 이전의 복잡한 (high variance) 뉴럴넷 구조를 $W^{[l]}=0$와 같이 특정 가중치를 줄여서 간단한 뉴럴넷 구조를 만들 수 있기에 regularization이 overfitting을 방지할 수 있다고 볼 수 있다.
  

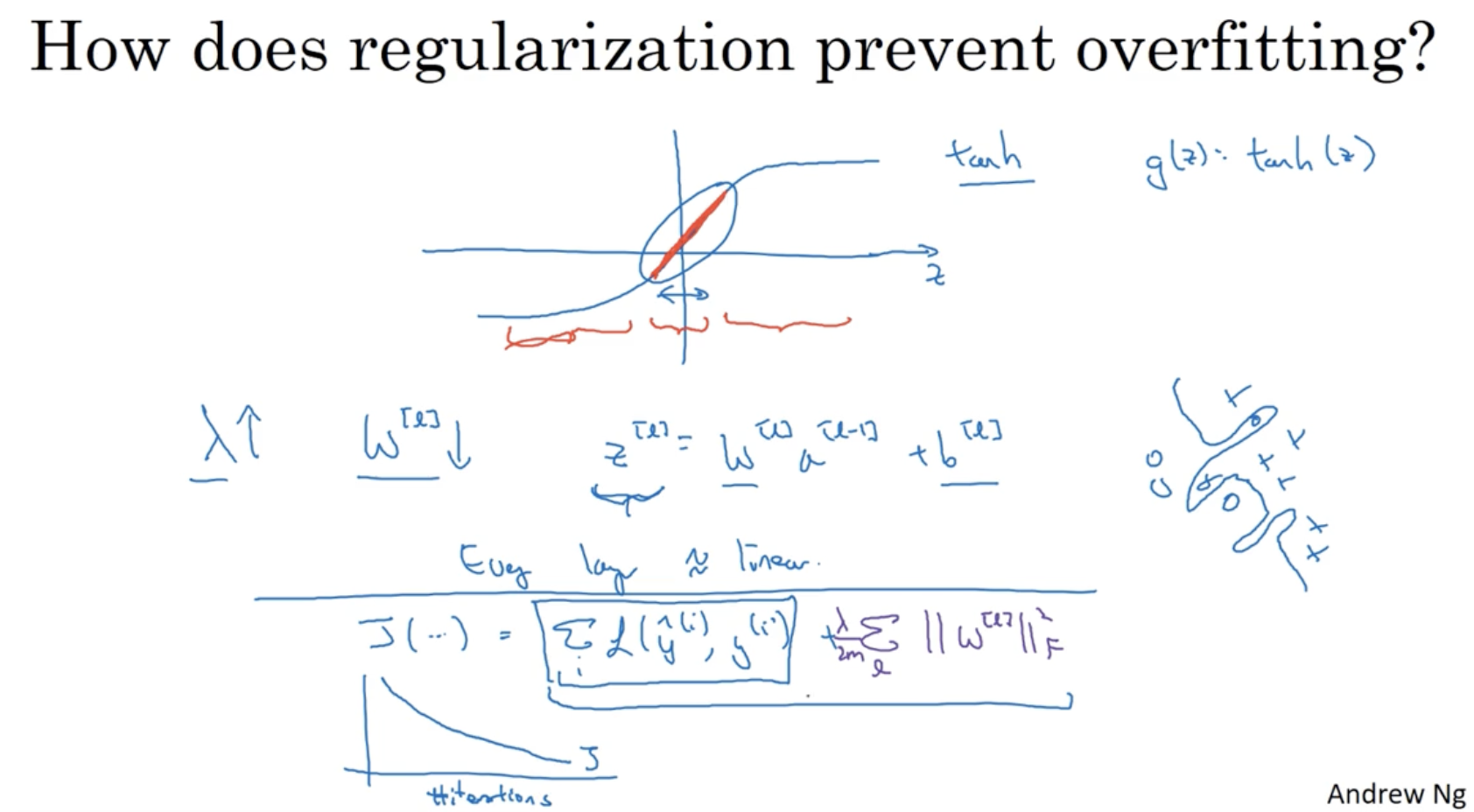
다음 내용도 regularization이 overfitting을 방지한다는 것을 보여주는 설명이다.

• $tanh$와 같은 activation function을 적용할 때, $z$값이 너무 크거나 너무 작으면 기울기가 0에 가까워진다. 이러한 경우 모델 구조는 더 복잡해질 것이다.
• 따라서 $\lambda$ 값을 늘리면 cost function에 의해서 $W^{[l]}$의 값을 더 줄이려고 할 것이고, 이렇게 되면 $z$의 값도 범위가 줄어든다. (너무 크거나 너무 작아지지 않게 된다.)
• 그리고 이로 인해 $tanh$의 값은 linear한 값이 나올 것이고, 따라서 모든 layer는 거의 linear한 구조를 이루게 된다. (= 단순한 구조를 이루게 된다.)
• 결론적으로 regularization $\lambda$의 값을 높이면 $W^{[l]}$의 값은 줄어들게 되고, 이로 인해 $tanh$와 같은 activation function은 linear한 구조를 띄며 모든 layer 역시 linear한 단순한 구조를 이루게 된다. 따라서 overfitting을 방지할 수 있다.
  

---

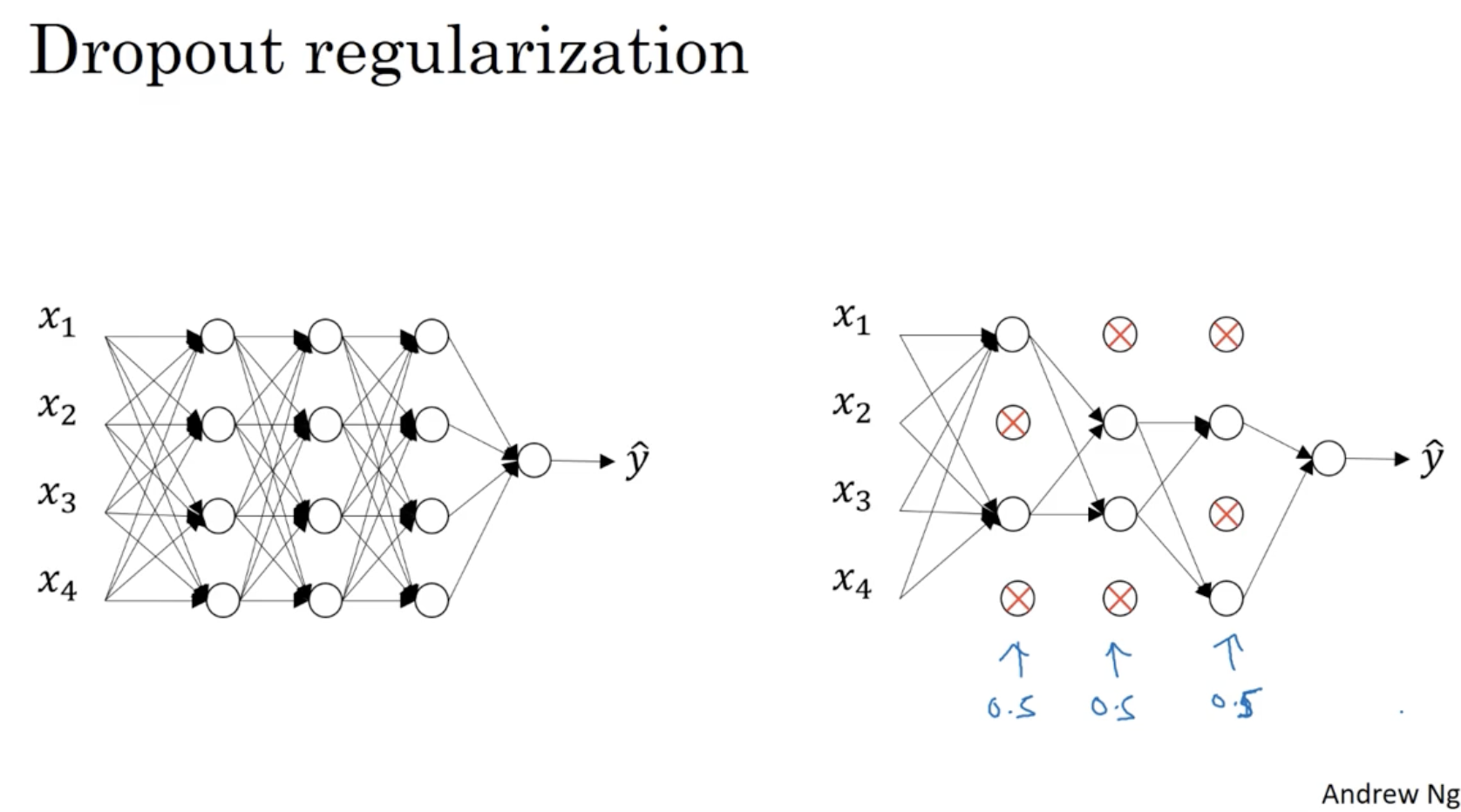
위에서는 L-2 regularization에 대해서 배웠다. 이제는 Dropout regularization에 대해서 알아본다.

• 아래와 같이 각 레이어마다 정해진 확률($0.5$)로 히든 레이어의 유닛을 drop한다.
• 0.5의 확률로 unit을 drop하면 좌측처럼 복잡했던 뉴럴넷이 우측처럼 단순해지는 것을 확인할 수가 있다. 따라서 overfitting을 방지할 수 있다.
• 이 방법이 dropout regularization 이다.
  

Inverted Dropout 을 구현하는 방법은 아래와 같다.

• keep_prob : 유지할 유닛의 확률 조건
• d3 = np.random.rand(a3.shpae[0], a3.shape[1]) < keep_prob :
  (a3.shpae[0], a3.shape[1]) 차원을 갖는 랜덤한 행렬을 만든 후 해당 값이 keep_prob보다 작은지를 확인한다. 모든 element의 값은 True or False로 나온다.
• a3 = np.multiply(a3, d3) :
  위에서 구한 d3를 기존의 a3에 element-wise product하여 전체 유닛 중 0.2 만큼의 유닛들을 drop한다.
• a3 /= keep_prob :
  $z^{[4]}=W^{[4]}a^{[3]}+b^{[4]}$ 에서, $a^{[3]}$은 80%만 유지되니 $z^{[4]}$에도 80%만 유지되도록 하기 위해 a3을 keep_prob(0.8) 만큼 나눠준다.
  

그리고 dropout 과정은 학습 과정 (forward propagation) 시에만 적용되며, test 과정에서는 적용되지 않는다.

아래와 같이 각 레이어마다 keep_prob 값을 달리 적용하면서 복잡한 레이어의 가중치를 줄일 수도 있다.

• 다만 cost function dropout에 따라 $J$를 재정의하는 것을 매우 복잡하기 때문에 최적의 dropout을 찾는 것은 직관에 의존할 수밖에 없다. (keep_prob을 1로 세팅하고 테스트해보고 0으로 세팅하고 테스트는 하는 등)
• 특히 컴퓨터 비전의 경우, 데이터의 차원이 매우 높기 때문에 dropout을 많이 적용하고 있다.
  

---

L-2 regularization 및 dropout regularization 뿐만 아니라 overfitting을 방지할 수 있는 방법은 여러 개가 존재한다.

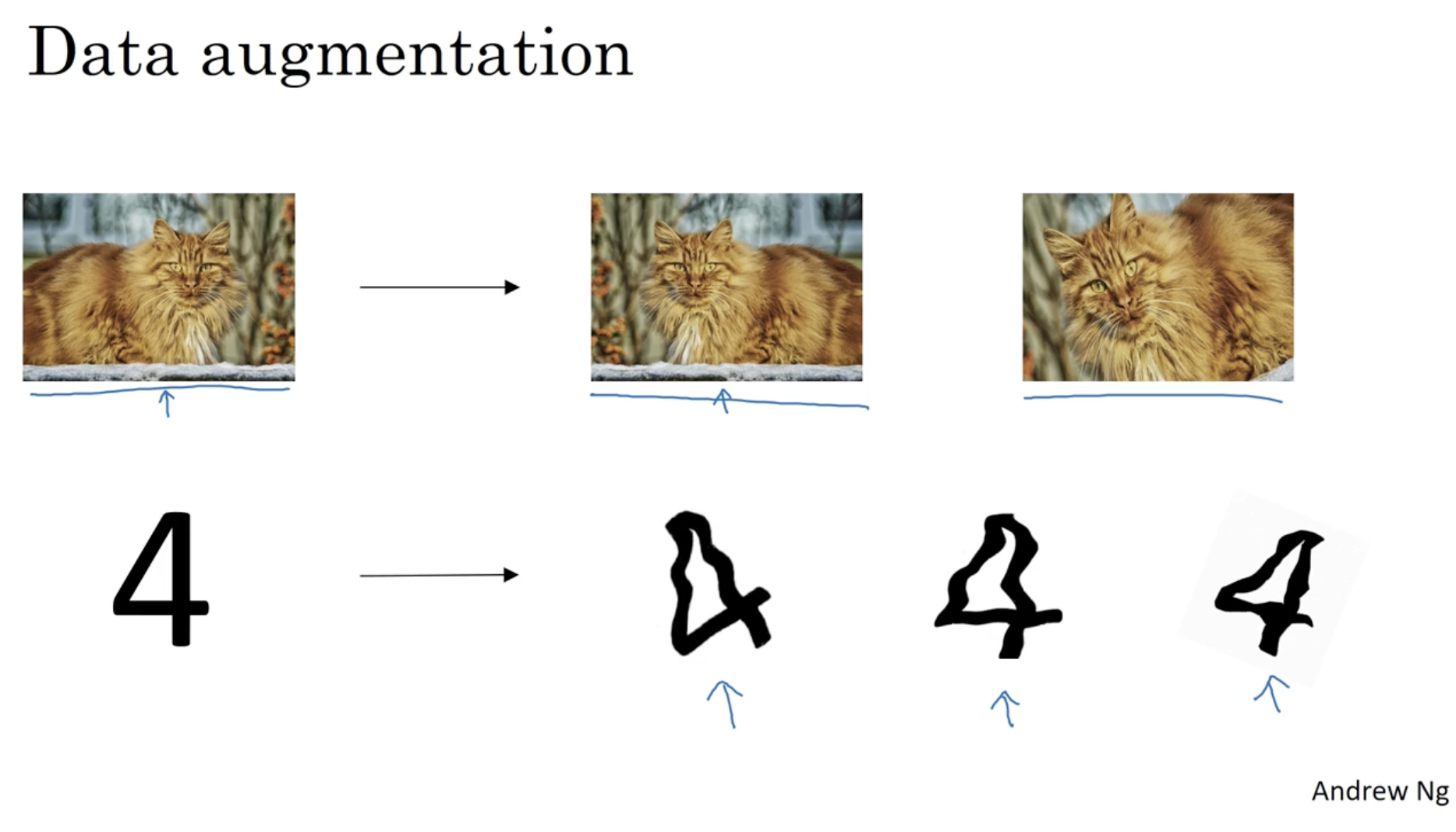
• 일반적으로 학습 데이터를 추가함으로써 overfitting을 방지할 수 있다.
• 하지만 데이터를 수집하는 것은 비용이 많이 들기 때문에 아래와 같이 기존의 데이터를 가지고 여러 데이터를 만드는 "Data Augmentation"을 적용하여 데이터를 증가시킬 수 있다.
  

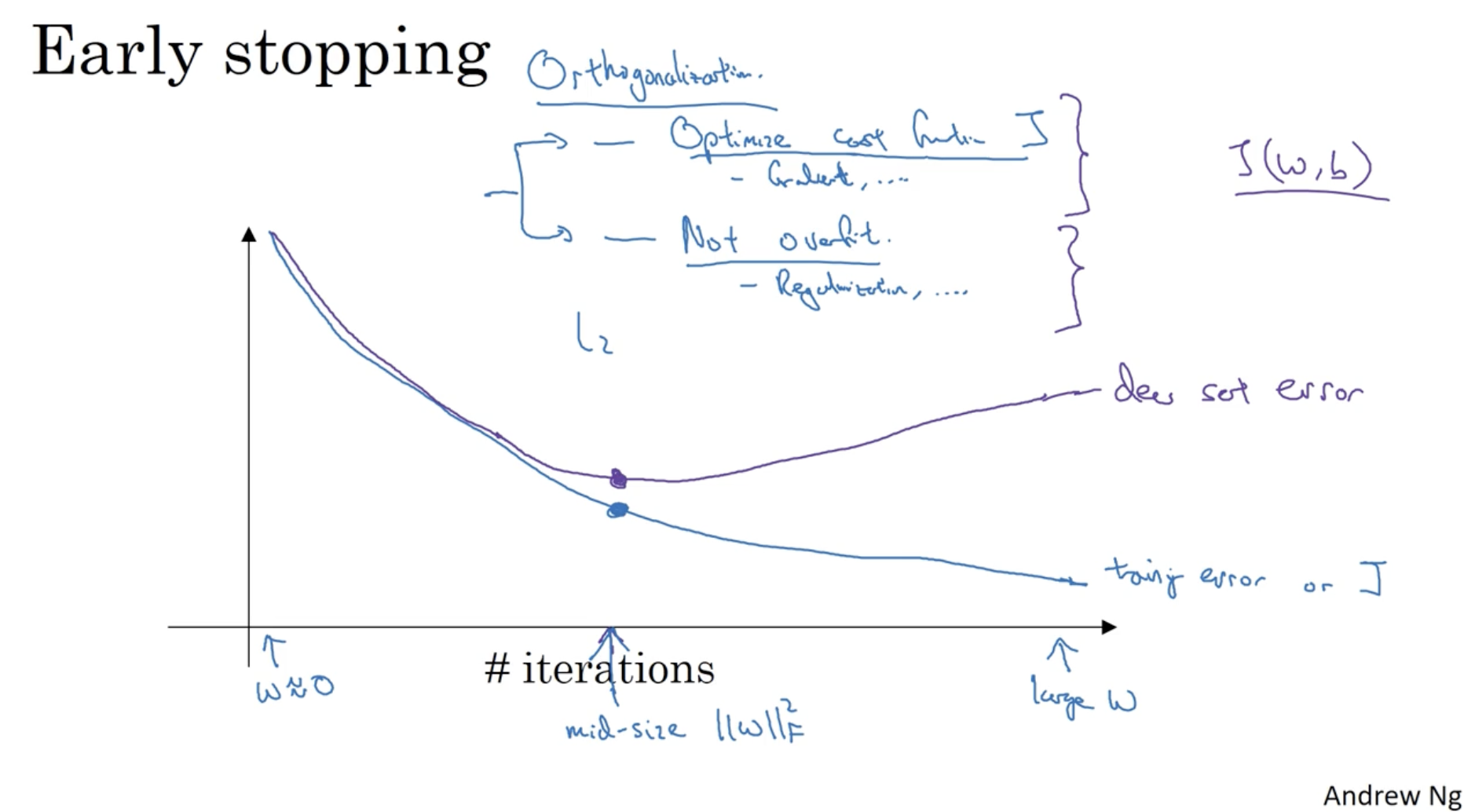
일반적인 모델 학습을 반복함에 따른 에러 값의 그래프는 아래와 같이 나온다. 일정 반복 이후로는 dev set error가 증가하는 모습을 보여준다.

• 따라서 dev set error가 증가하기 전에 모델 학습을 중지하는 것도 overfitting을 방지하는 방법 중 하나이다.
• 이 경우, 특별한 optimize 방법이나 regularization 방법이 적용되지는 않지만 계산 비용을 아낄 수 있다는 장점이 존재한다.
  

---

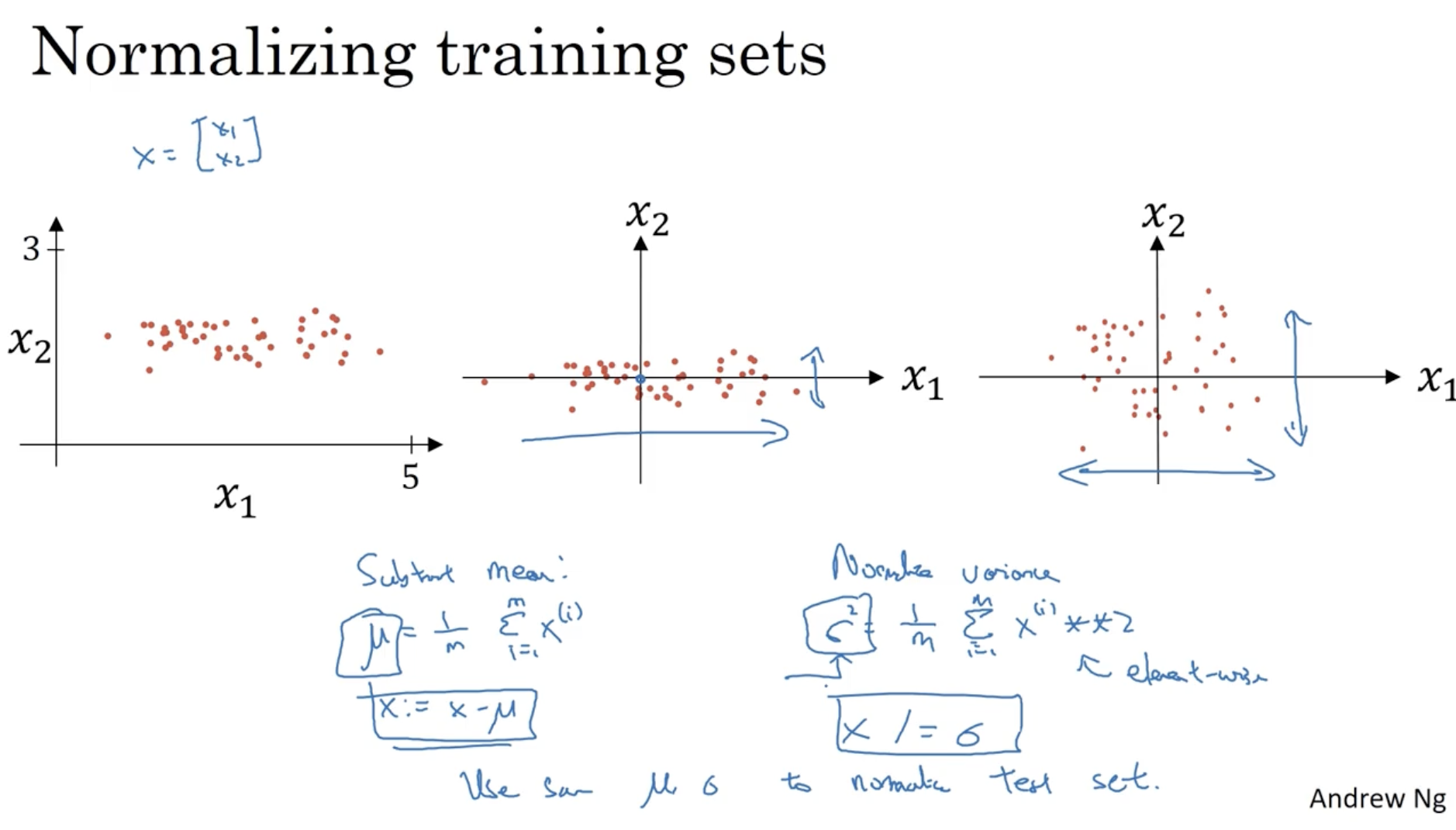
모델을 효과적으로 학습하기 위해서는 입력 데이터의 normalization이 필요하다.

• ex. $x := \frac{x-\mu}{\sigma}$
• 그리고 train set에서 적용된 $\mu, \sigma$를 test set에 대해서도 동일하게 적용한다.
  

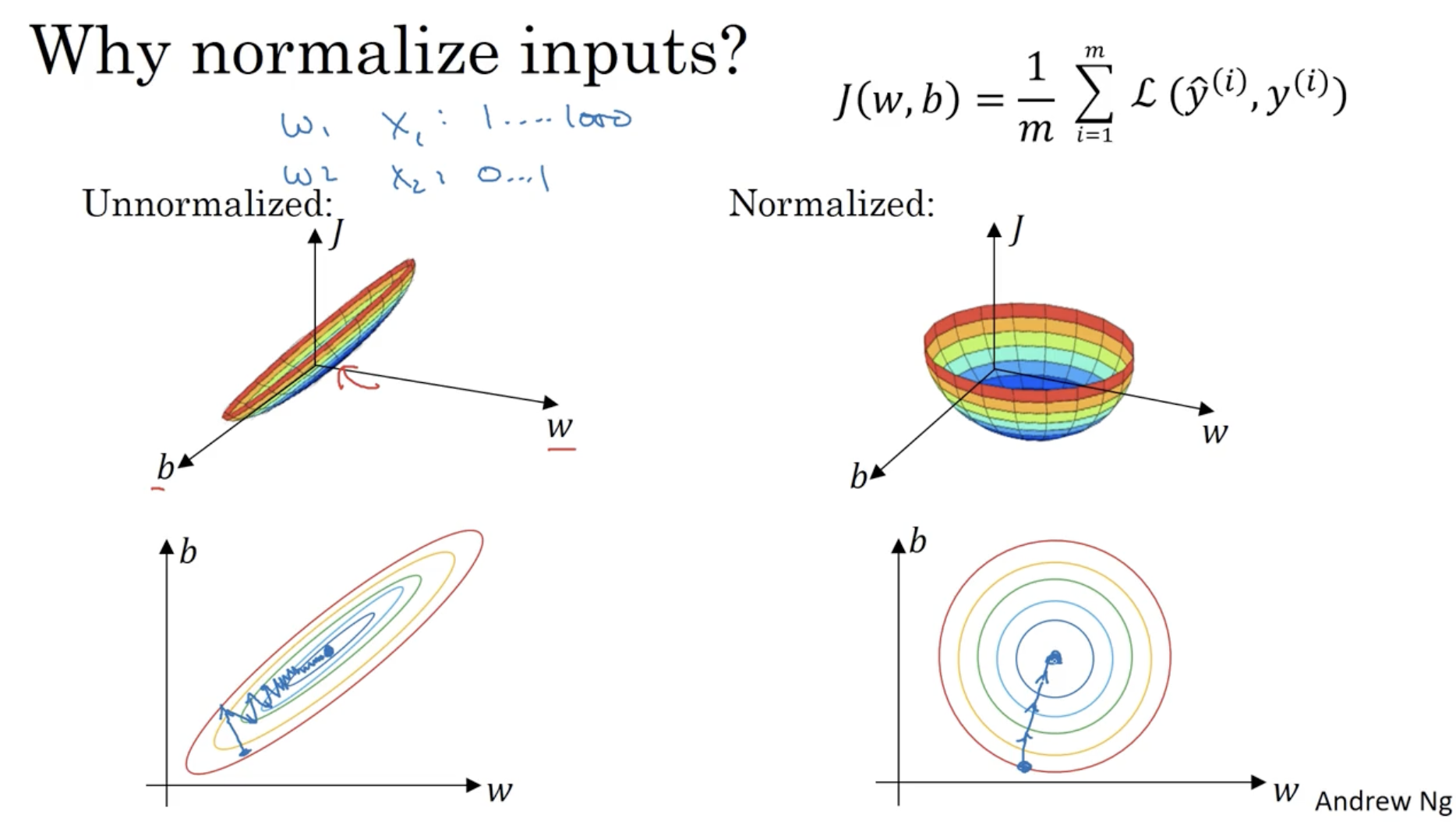
cost function $J(w,b)$는 파라미터 $w,b$에 따라 값이 변한다.

• 따라서 만약 input data normalization이 적용되지 않을 경우, 좌측처럼 특정 파라미터에 의해서만 $J$ 값이 크게 변하고, 다른 파라미터에 대해서는 $J$ 값의 변화가 거의 없는 것처럼 나올 수 있다. 이처럼 unblanced한 cost function에 대하여 gradient descent alg.을 적용하면 gradient의 스텝이 이상하게 나타날 수 있다.
• 반면에 우측처럼 normalization을 적용하면, balanced한 cost function이 나타날 것이며, gradient descent를 적용하면 균형잡힌 방향으로 global optima를 찾을 것이다.
  

---

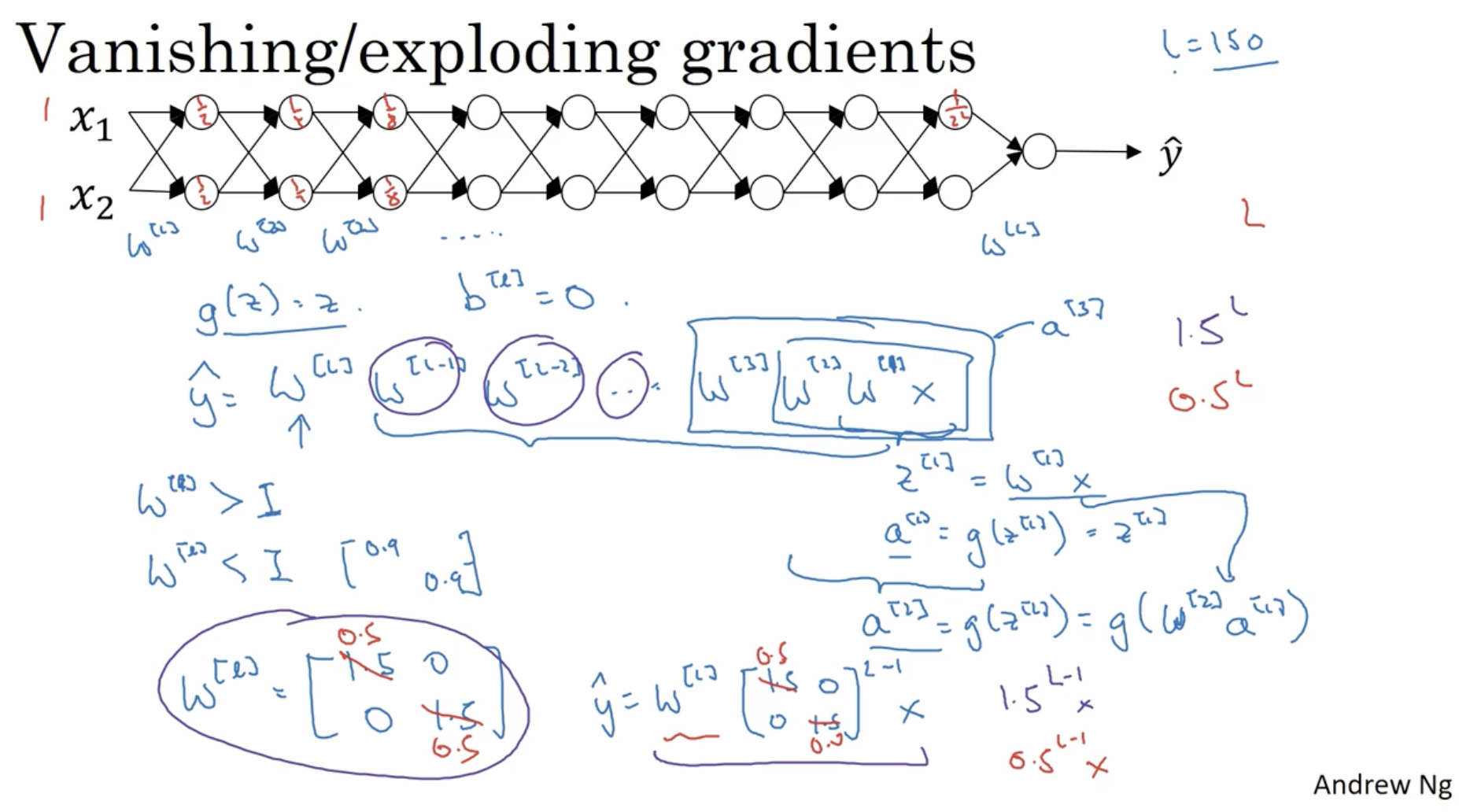
gradient descent를 적용할 때, gradient가 0에 가까워지거나 혹은 exponential하게 커지는 경우가 있다.

• 예를 들어 activation function은 $g(z)=z$ 와 같고, $b^{[l]}=0$ 이라고 가정해보자.
• 이 경우 $W^{[l]}>I (=W^{[l]}>1)$ 이면 $\hat y$의 값은 exponential하게 증가할 것이고,
• $W^{[l]}<I (=W^{[l]}<1)$ 이면 $\hat y$의 값은 0에 가까워져 소멸할 것이다.
• 이 문제는 뉴럴넷의 고질적인 문제점이다. 따라서 적정한 $W^{[l]}$로 초기화해야 한다.
  

---

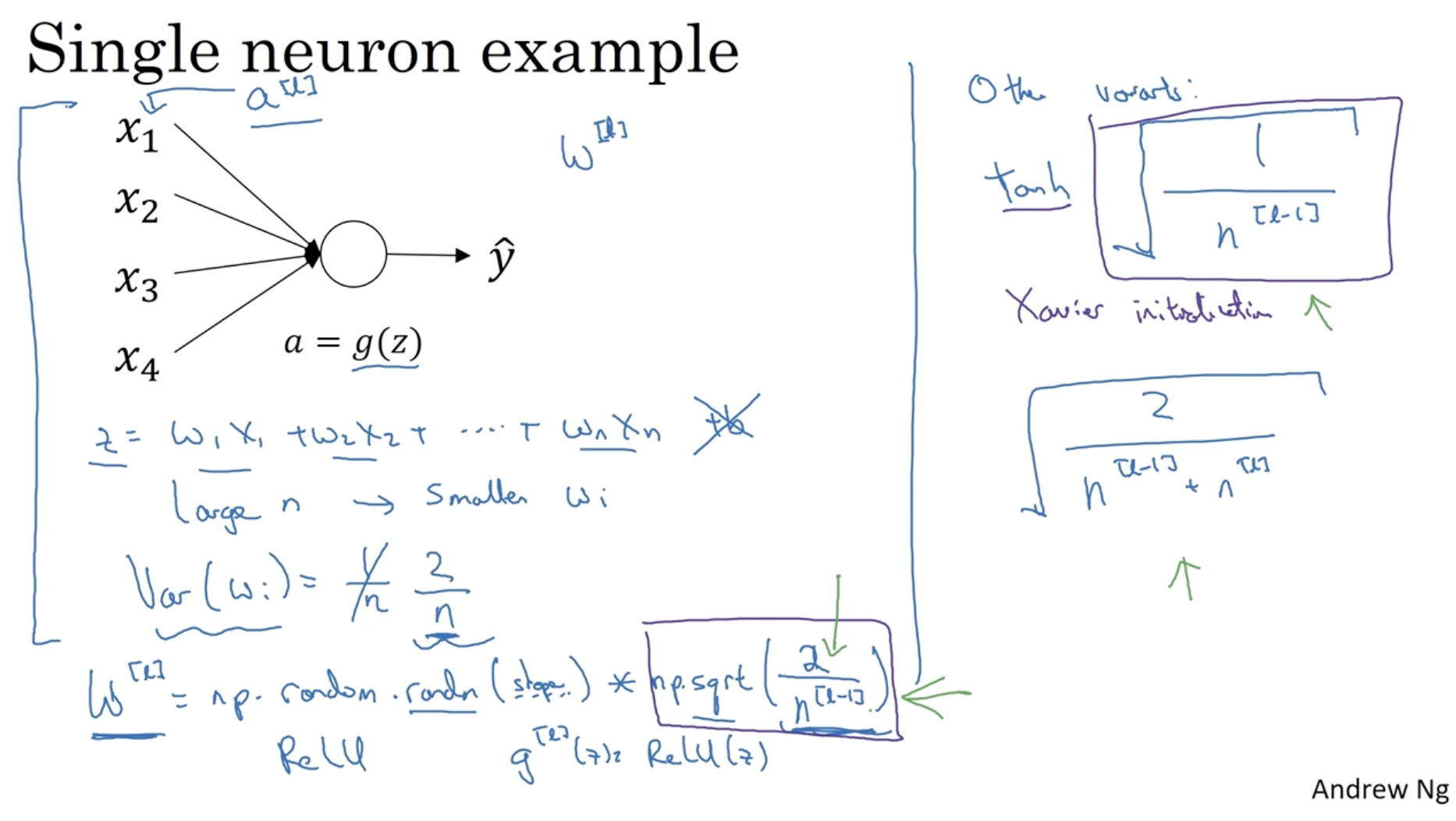
single neuron을 예로 들어보자.

• 아래와 같이 $z=w_1x_1+w_2x_2+...+w_nx_n$과 같이 나올 것이다. ($b=0$ 가정)
• 따라서 $n$이 커지면 그 만큼 항이 늘어나게 되고, $z$값이 증가하는 것을 막기 위해 $w$는 $n$에 반비례해서 작아질 것이다. (만약 $n$이 작아지면 $w$은 커진다.)
• 따라서 $var(w:)=\frac{1}{n}$으로 볼 수 있다. (반비례 관계 의미)
  • 다만 ReLU activation function에서는 $var(w:)=\frac{2}{n}$로 적용하는 게 더 효과적이다.
• 그리하여 $W^{[l]}$을 다음과 같이 초기화하면 된다.
  • $W^{[l]}=np.random.randn(shape)*np.sqrt(\frac{2}{n^{[l-1]}})$ (in ReLU)
  • $W^{[l]}=np.random.randn(shape)*np.sqrt(\frac{1}{n^{[l-1]}})$ (in tanh) (= Xavier initialization )
  • or somthing like that. ($\sqrt\frac{2}{n^{[l-1]}+n^{[l]}}$)
    

---

다음은 gradient를 체크하는 방법(gradient checking)이다. 즉, 기울기가 올바르게 나온다는 것을 증명하는 방법이다.

• 우선 $W, b$를 $\Theta$로 $dW, db$를 $d\Theta$로 하여 하나로 묶는다.(concatenate)
  

다음으로 하나의 $\theta_i$에 대하여 $\epsilon$ 값을 더하고 빼서, 기울기 값을 구하여 이를 $d\theta_{approx}[i]$에 저장한다.
그리고 backpropagation에서 구한 $d\theta$와 $d\theta_{approx}$를 유클리드 거리로 비교하여 차이값을 통해 backpropagation에서 구한 기울기가 올바르다는 것을 증명할 수 있다.

• 따라서 grad checking을 통해 디버깅할 수 있다.
  

---

grad checking의 주요 고려 사항은 다음과 같다.