[딥러닝] Neural Networks and Deep Learning Week 4

출처 : https://www.coursera.org/specializations/deep-learning

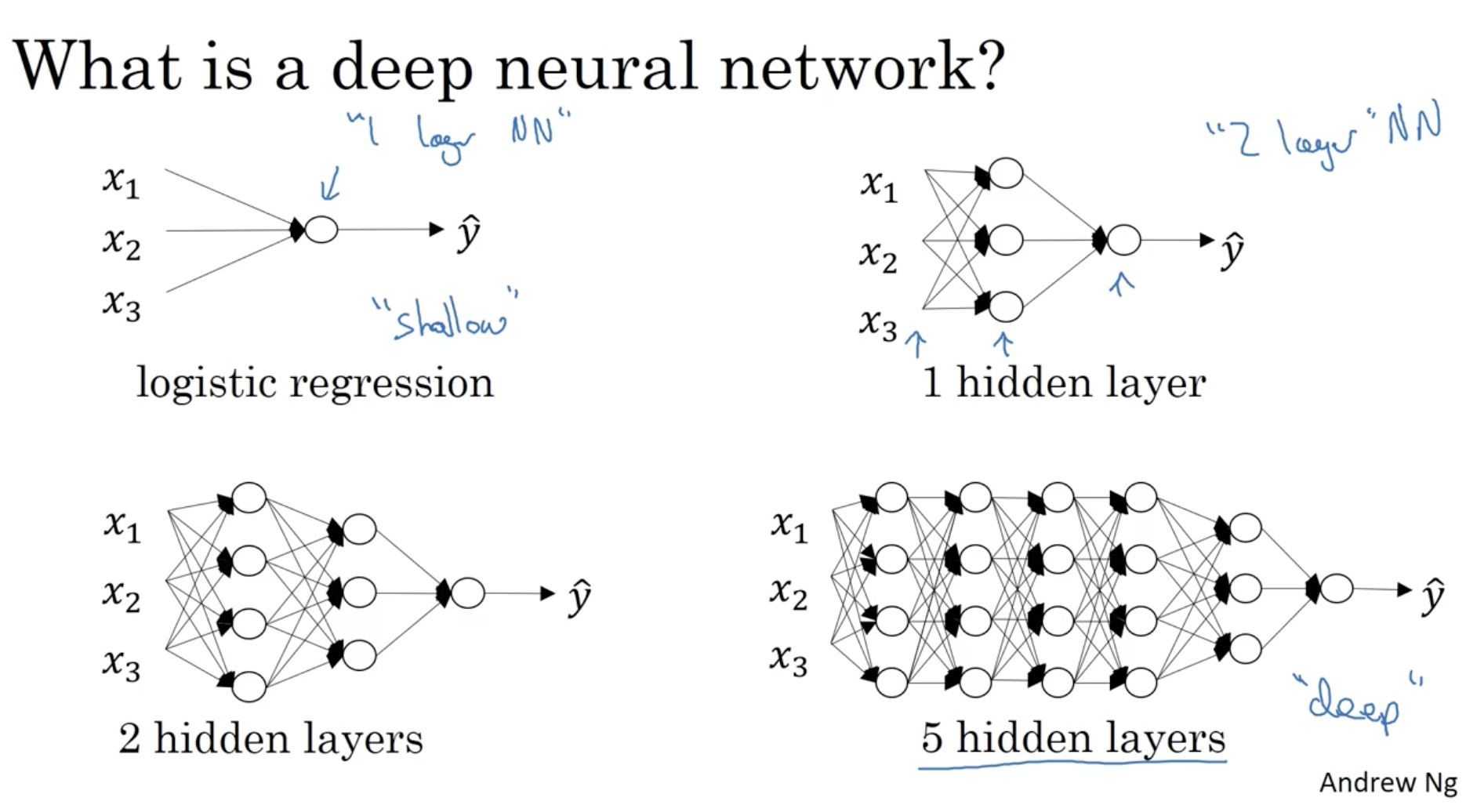
딥러닝이란 무엇일까? 아래 그림을 보자.

• 좌측 상단 : logistic regression 모델을 보여주며, 이는 "1 layer NN(Neural Networks)"를 의미한다.
• 우측 상단 : hidden layer가 1개인 "2 layer NN"을 의미한다.
• 좌측 하단 : hidden layer가 2개인 "3 layer NN"을 의미한다.
• 우측 하단 : hidden layer가 5개인 "6 layer NN"을 의미한다.
• 이처럼 layer 수가 적은 모델은 "shallow"하다고 하며, layer 수가 많은 모델을 "deep"하다고 한다.
  

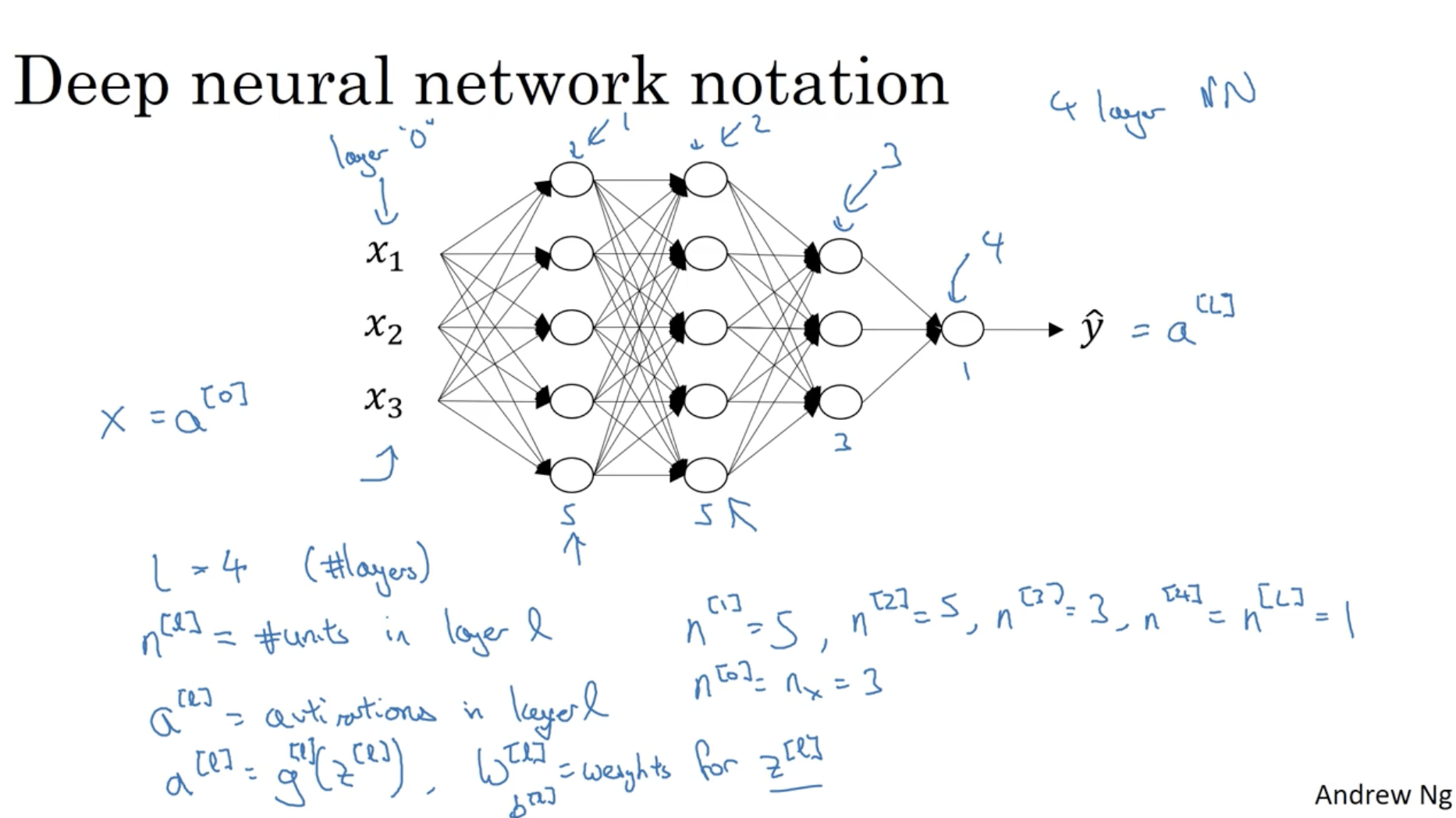
Deep neural network의 notation은 다음과 같다.

• $L : \text{number of layers}$
• $n^{[l]} : \text{number of units in layer $l$}$
• $a^{[l]} : \text{activation in layer $l$}$
• $g^{[l]} : \text{activation function in layer $l$}$
• $z^{[l]} : \text{result of $z^{[l]}={w^{[l]}}a^{[l-1]}+b^{[l]}$}$
• $w^{[l]} : \text{weights for $z^{[l]}$}$
• $b^{[l]} : \text{biases for $z^{[l]}$}$
  

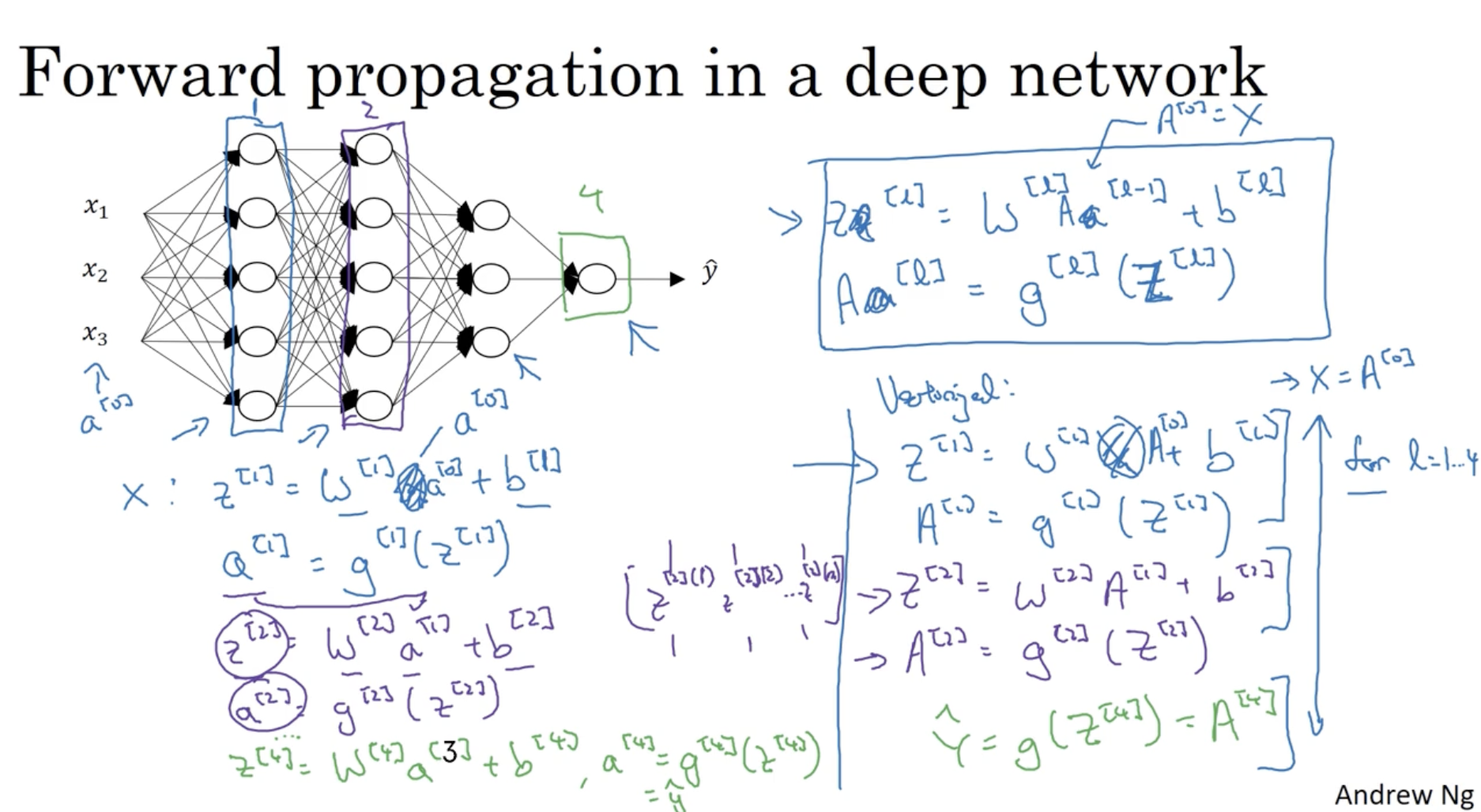
다음은 Forward propagation에 대한 설명이다.

• $Z^{[l]}=W^{[l]}A^{[l-1]}-b^{[l]}$
• $A^{[l]}=g^{[l]}(Z^{[l]})$
• 위 두 식을 이용하여 $l=1 \to l=L$까지 반복하며, 모든 레이어의 유닛값을 구한다.
• 그리하여 최종 예측값 $A^{[L]}=g^{[L]}(Z^{[L]})=\hat Y$ 값을 구한다.
  

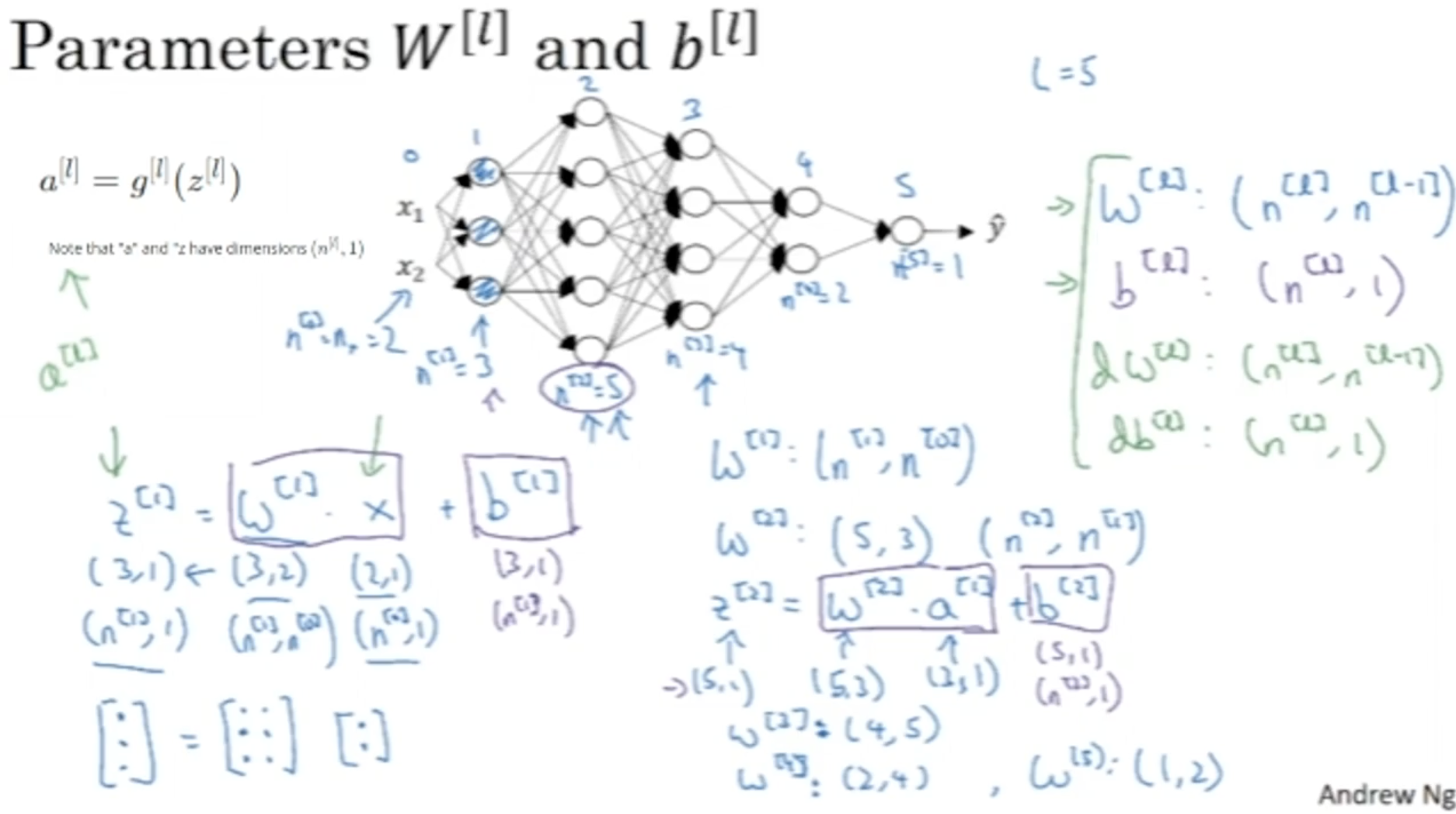
딥 뉴럴넷 모델을 만들다 보면 차원이 헷갈릴 때가 많다. 따라서 차원 개념을 따로 정리한다. 아래는 parameter $W,b$의 차원에 대한 내용이다.

• $W^{[l]}:(n^{[l]}, n^{[l-1]})$
• $b^{[l]}:(n^{[l]}, 1)$
• 그리고 $dW,db$의 차원은 $W,b$의 차원과도 같다. 따라서 다음과 같이 작성할 수 있다.
• $dW^{[l]}:(n^{[l]}, n^{[l-1]})$
• $db^{[l]}:(n^{[l]}, 1)$
  

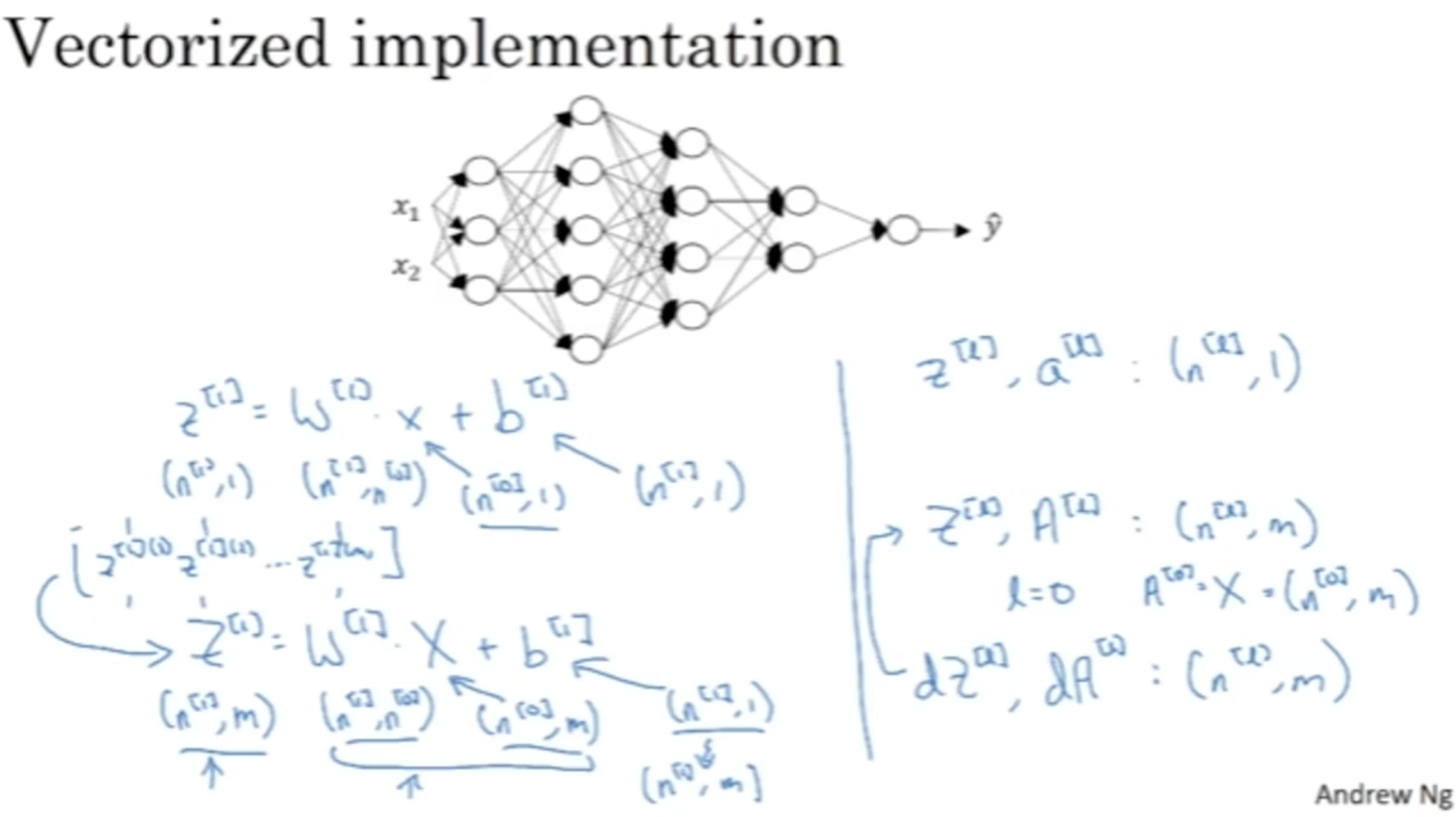
다음으로 $Z, A$의 차원을 알아본다. ($m$개의 데이터에 대한 vectorized가 적용된 것이다.)

• $Z^{[l]},A^{[l]}:(n^{[l]}, m)$
• $dZ^{[l]},dA^{[l]}:(n^{[l]}, m)$
• $m$개의 데이터에 대한 vectorized가 적용되어도 $b^{[l]}$의 차원은 $(n^{[l]},1)$인데, 이 이유는 python의 broadcasting 에 의하여 자동으로 $(n^{[l]},1)\rightarrow (n^{[l]},m)$으로 변환되기 때문이다.
  

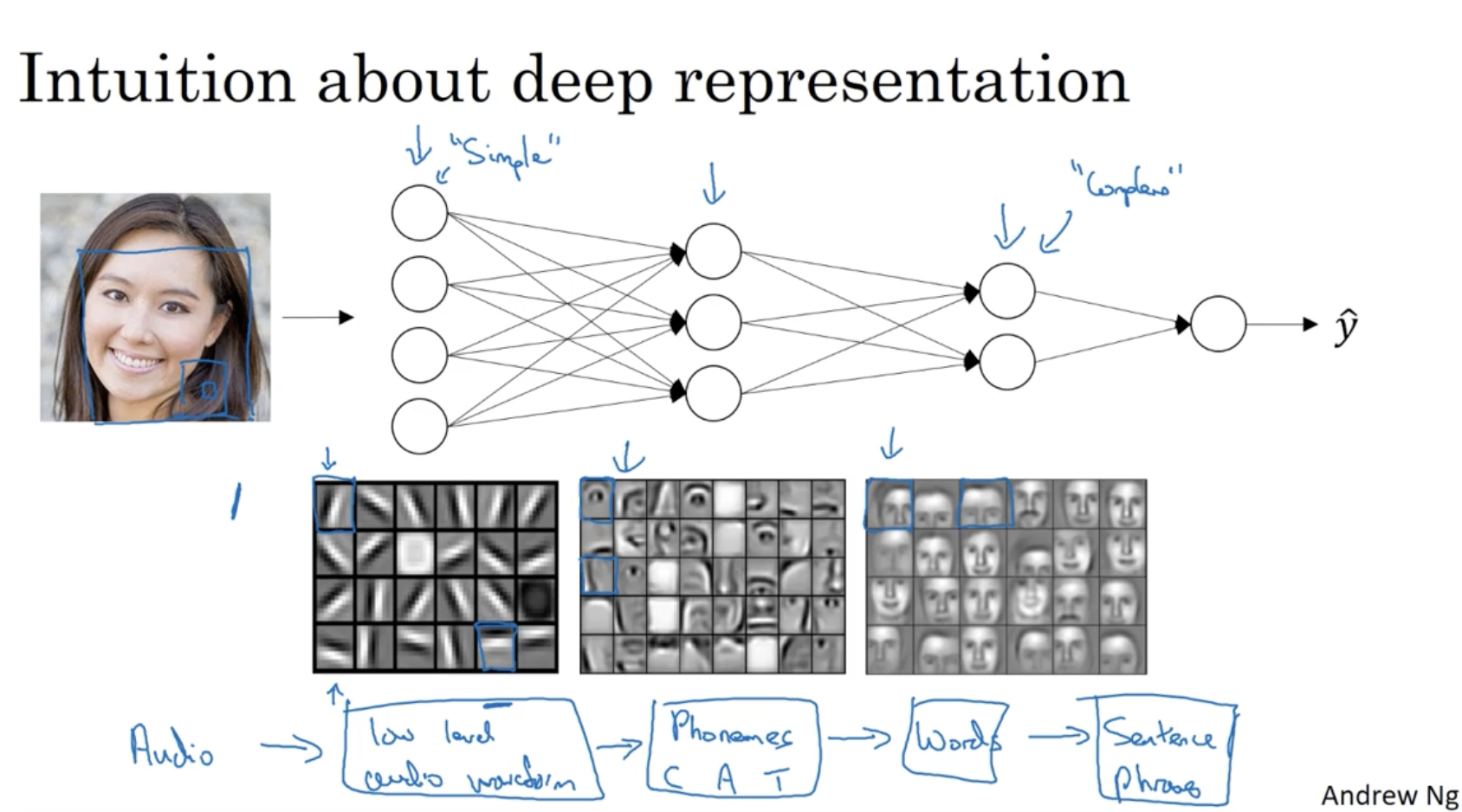
딥러닝의 예측 과정을 개략적으로 살펴보면 다음과 같다.

• 이미지 데이터가 들어올 때, 1 layer에서 edge를 detect한다. (simple, small window)
• 2 layer에서 눈, 코, 입 등 좀더 복잡한 구조를 detect한다.
• 마지막 3 layer에서 사람의 얼굴을 detect한다. (complex, large window)
• 이처럼 simple하게 시작하여 마지막에 complex하게 representation하는 게 딥러닝의 구조이다.
• 또한 이미지 데이터뿐만 아니라 오디오 데이터도 다음과 같이 적용될 수 있다.
  • Audio -> 음성의 높낮이 탐지 -> 형태소 탐지 -> 단어 탐지 -> 문장 탐지
    

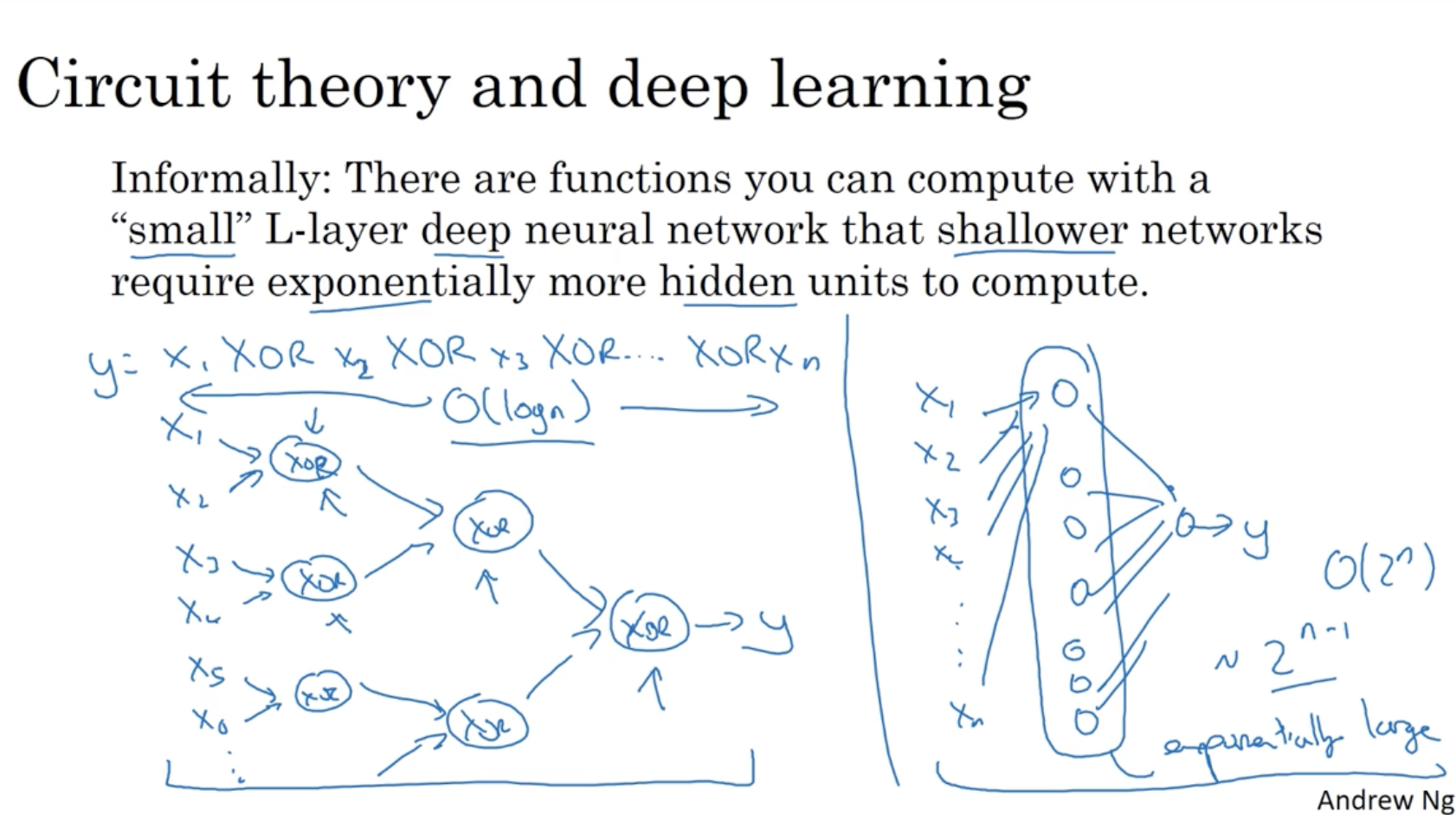
딥러닝이 효과적인 이유를 간단히 설명하면 다음과 같다.

• 좌측처럼 deep 하게 모델을 구성할 경우 복잡도는 $O(log \ n)$이다.
• 하지만 우측처럼 shallow (일반적인 logistic regression) 하게 모델을 구성할 경우 복잡도는 $O(2^n)$이다.
• 따라서 deep learning이 더 효과적이라고 볼 수 있다.
  

forward and backward propagation 과정을 살펴보자.

• forward propagation in layer $l$
  • 필요한 parameter : $W^{[l]}, b^{[l]}$
  • input : $a^{[l-1]}$
  • output : $a^{[l]}$
  • cache : $z^{[l]}(W^{[l]},b^{[l]})$ (back propagation을 위해 필요함.)
• backward propagation in layer $l$
  • 필요한 parameter 혹은 value : $W^{[l]},b^{[l]},z^{[l]}$
  • input : $da^{[l]}$
  • 계산 : (by $da^{[l]}$) $\rightarrow dz^{[l]}$
  • output : $da^{[l-1]}$,
    (by $W^{[l]},b^{[l]},dz^{[l]}$) $\rightarrow dW^{[l]}, db^{[l]}$
    

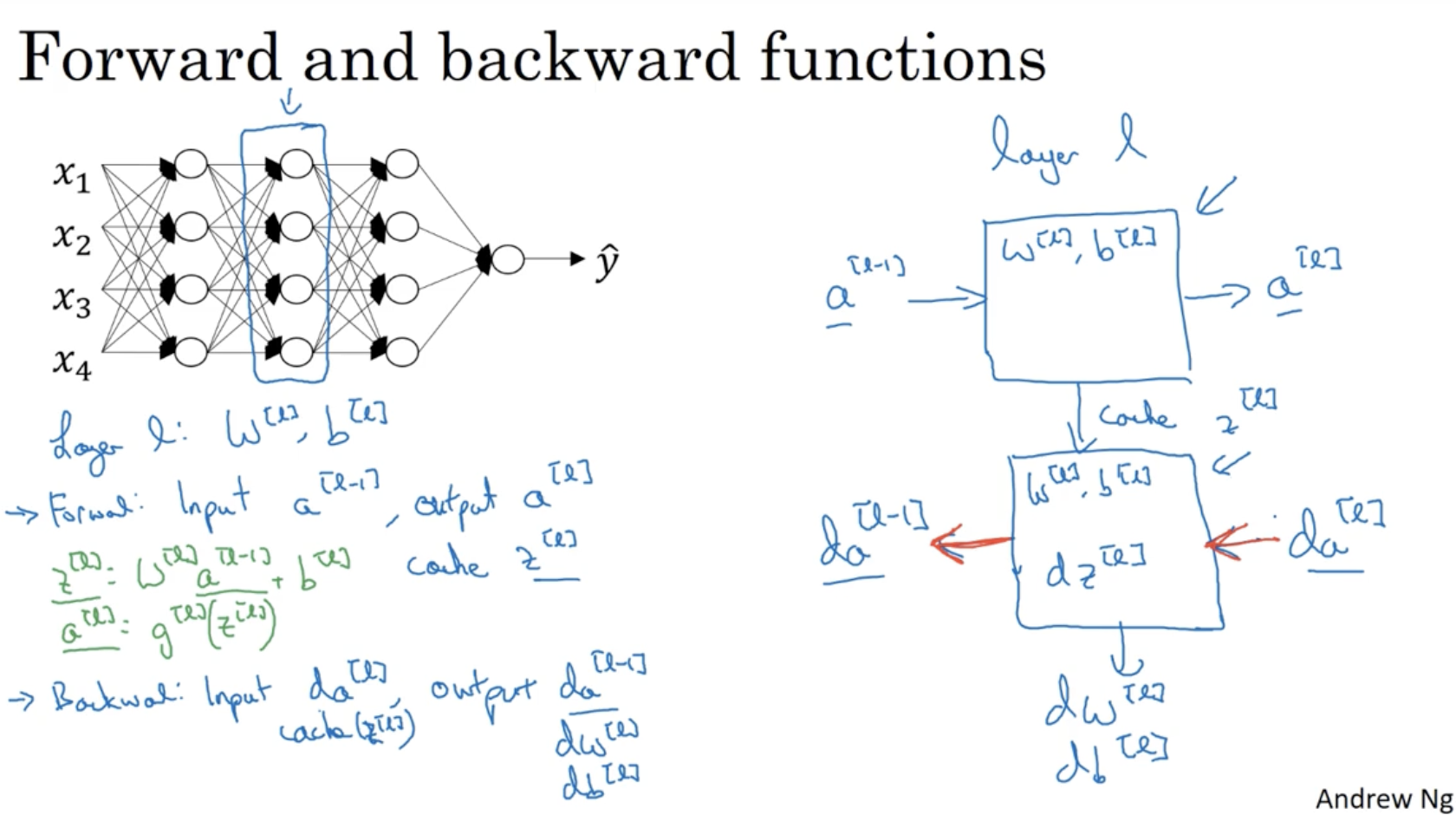
아래는 deep neural network의 forward and backward propagation의 과정을 잘 설명하는 그림이다. 참고하면 좋을 것 같다.

• forward propagation -> backward propagation -> gradient descent -> ...
  

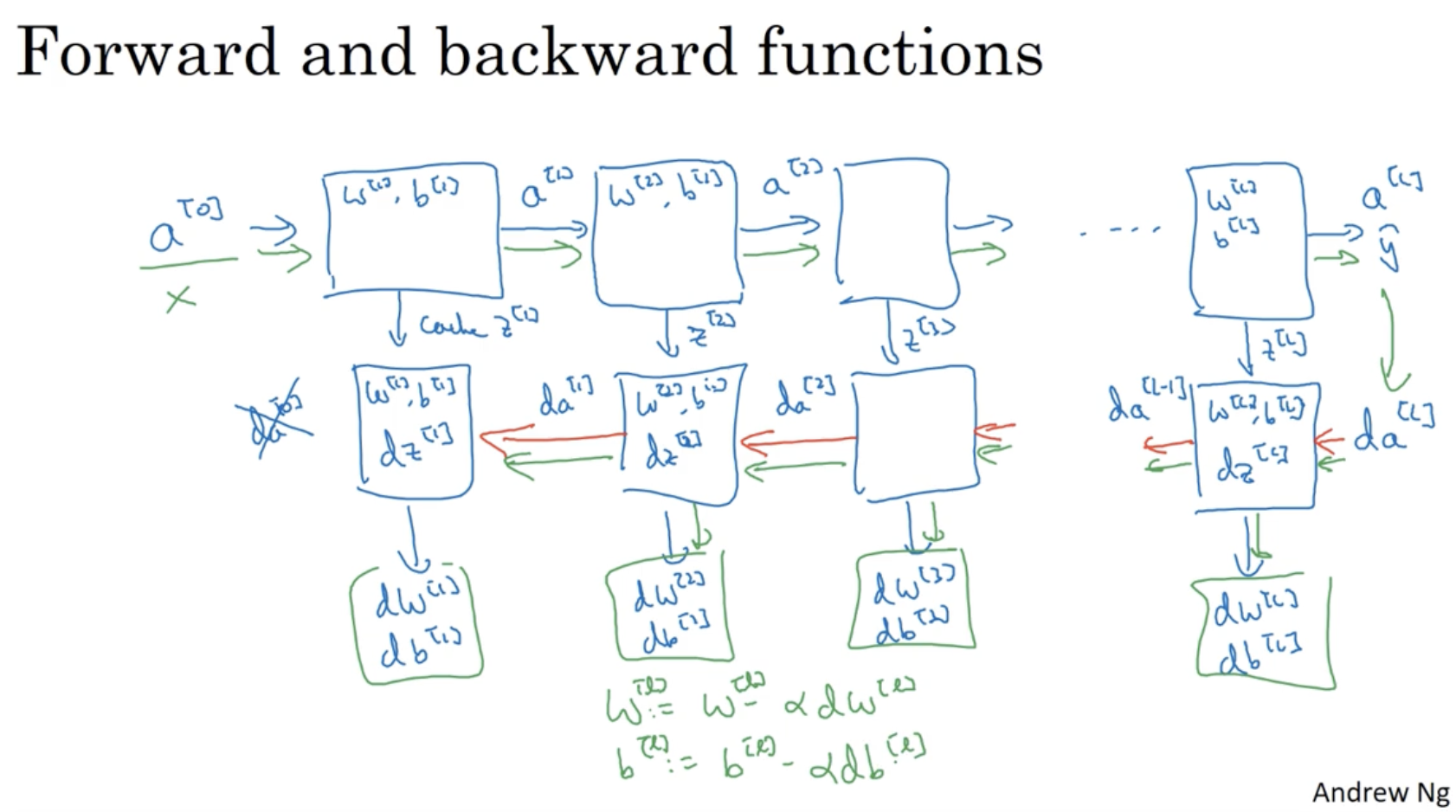
layer $l$에서의 forward propagation을 정리하면 다음과 같다.

• non-vectorization
  • $z^{[l]}=W^{[l]}a^{[l-1]}+b{[l]}$
  • $a^{[l]}=g^{[l]}(z^{[l]})$
• vectorization
  • $Z^{[l]}=W^{[l]}A^{[l-1]}+b{[l]}$
  • $A^{[l]}=g^{[l]}(Z^{[l]})$
    

layer $l$에서의 backward propagation을 정리하면 다음과 같다.

• non-vectorization
  • $dz^{[l]}=da^{[l]}*g'^{[l]}(z^{[l]})$ ($*$ : element-wise product)
  • $dW^{[l]}=dz^{[l]}{a^{[l-1]}}^T$
  • $db^{[l]}=dz^{[l]}$
  • $da^{[l-1]}={W^{[l]}}^Tdz^{[l]}$
• vectorization
  • $dZ^{[l]}=dA^{[l]}*g'^{[l]}(Z^{[l]})$
  • $dW^{[l]}=\frac{1}{m}dZ^{[l]}{A^{[l-1]}}^T$
  • $db^{[l]}=\frac{1}{m}np.sum(dz^{[l]}, \ axis=1, \ keepdims=True)$
  • $dA^{[l-1]}={W^{[l]}}^TdZ^{[l]}$
    

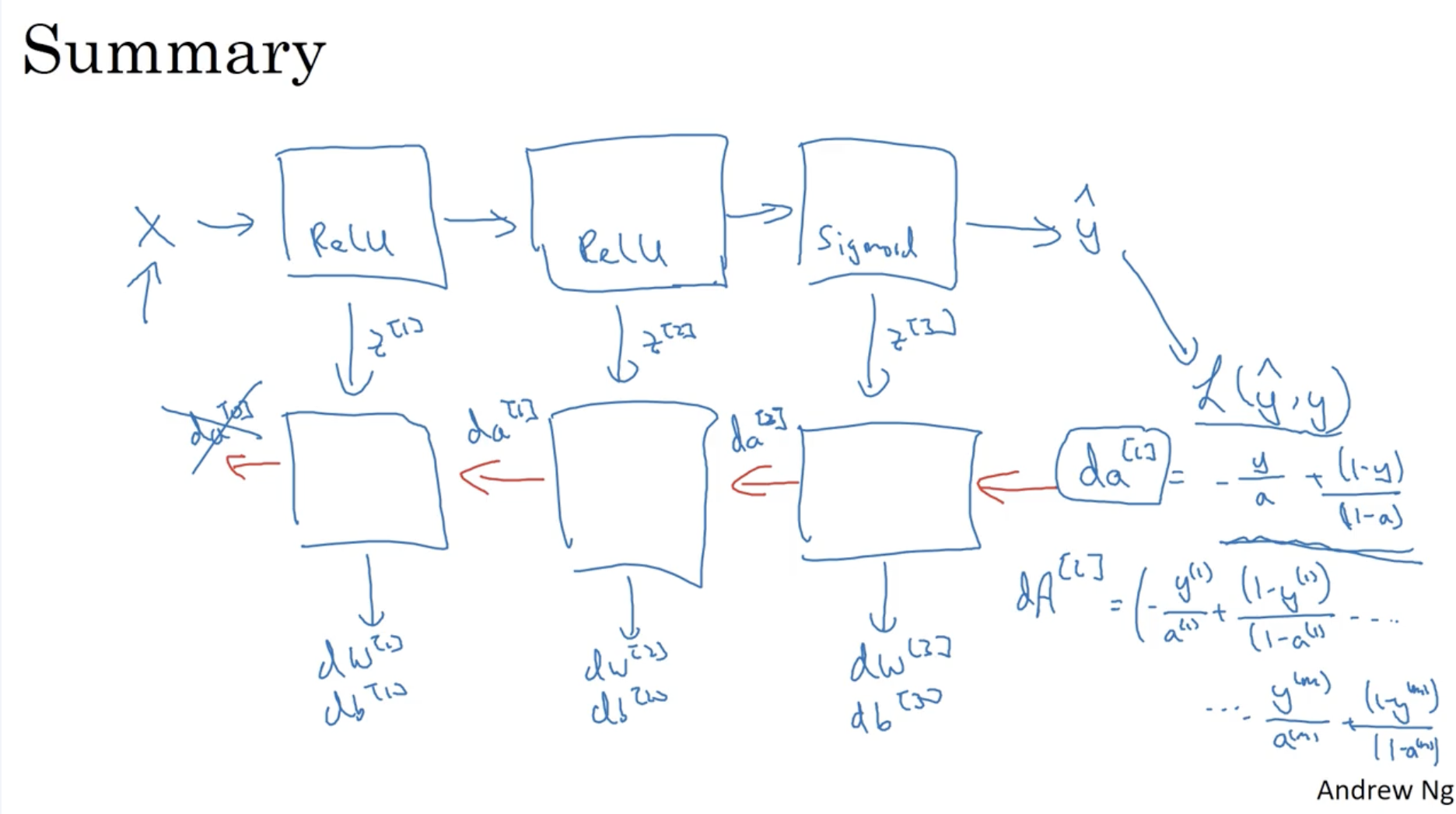
따라서 요약하면 다음과 같다.

• X -> forward propagation -> Cal. Loss -> backward propagation -> gradinent descent -> ...
  

딥러닝에는 hyperparameter 라는 개념이 존재한다. 하이퍼 파라미터의 예시는 다음과 같다.

• learning rate $\alpha$
• epochs (# of iterations)
• # of hidden layers $L$
• # of hidden units $n^{[1]},n^{[2]},...$
• choice of hidden function in layer $l$
  

하이퍼 파라미터의 값에 따라 우측 그래프처럼 모델의 정확도가 다양하게 나타날 수 있다.