[딥러닝] Improving Deep Neural Networks: Hyperparameter Tuning, Regularization and Optimization Week 2

출처 : https://www.coursera.org/specializations/deep-learning

mini batch gradient descent는 $m$개의 데이터를 $x$개의 묶음으로 나눠서 gradient descent를 적용하는 방법이다.

• 아래 예시에서 총 5,000,000개의 데이터를 1,000개의 mini batch로 묶는 방법을 알아보자.
• 데이터는 다음과 같이 존재한다.
  • $X=[x^{(1)}x^{(2)}...x^{(m)}] \in \mathbb{R}^{n_x\times m}$
  • $Y=[y^{(1)}y^{(2)}...y^{(m)}] \in \mathbb{R}^{1\times m}$ (정확히 표현하면 1이 아니라 $\text{\# of classes}$ 이다.)
• 그리고 여기에 1,000 크기의 mini-batch 를 적용하면 다음과 같다.
  • $X^{\{1\}}=[x^{(1)}...x^{(1000)}] \in \mathbb{R}^{n_x \times 1000}$, $Y^{\{1\}}=[y^{(1)}...y^{(1000)}] \in \mathbb{R}^{1 \times 1000}$
  • $X^{\{2\}}=[x^{(1001)}...x^{(2000)}] \in \mathbb{R}^{n_x \times 1000}$, $Y^{\{2\}}=[y^{(1001)}...y^{(2000)}] \in \mathbb{R}^{1 \times 1000}$
  • ... $X^{\{5000\}}=[...x^{(m)}] \in \mathbb{R}^{n_x \times 1000}$, $Y^{\{5000\}}=[...y^{(m)}] \in \mathbb{R}^{1 \times 1000}$
• 즉, $t$ 번째 mini-batch를 다음과 같이 표기한다. $X^{\{t\}}, Y^{\{t\}}$
  

다음은 mini batch에 gradient descent를 적용하는 예시이다.

• $t=1 \to t=5000$ range로 gradient descent alg.을 수행한다.
• 먼저 forward propagation을 수행한다. (batch size가 1000이므로 1000개의 데이터에 대해서 vectorization이 적용된 방법으로 수행한다.)
  • $Z^{[1]}=W^{[1]}X^{\{t\}}+b^{[1]}$
  • $A^{[1]}=g^{[1]}(Z^{[1]})$
  • ...
  • $A^{[L]}=g^{[L]}(Z^{[L]})$
• 다음으로 Cost function $J^{\{t\}}$ 값을 구한다.
  • $J^{\{t\}}=\frac{1}{1000}\sum_{i=1}^{1000}L(\hat y^{(i)}, y^{(i)})+\frac{\lambda}{2\times 1000}\sum_{l=1}^{L}{||W^{[l]}||}_2^2$
• 그리고 back propagation을 적용하여 $dW, db$ 값을 구한다.
• 마지막으로 $dW, db$ 값을 가지고 gradient descent alg.을 적용한다.
  • $W^{[l]}=W^{[l]}-\alpha \ dW^{[l]}$, $b^{[l]}=b^{[l]}-\alpha \ db^{[l]}$
• 이렇게 foward propagation ~ gradient descent 과정까지를 하나의 "epoch"이라고 한다.
• 따라서 epoch 수에 맞춰 모델을 학습한다.
  

---

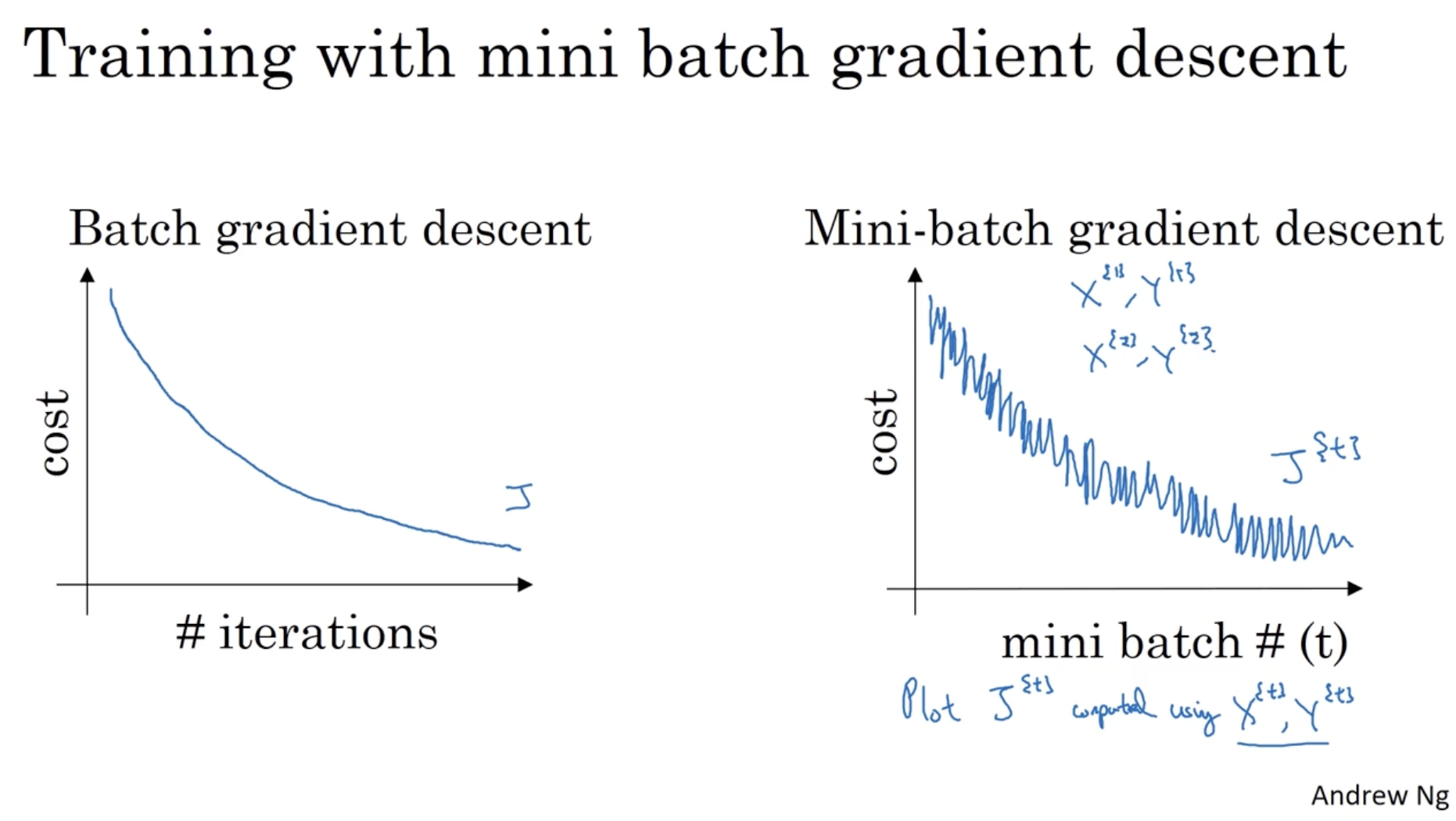
batch gradient descent 와 mini-batch gradient descent 의 학습 과정에 따른 cost function $J,J^{\{t\}}$ 값의 그래프는 아래와 같다.

• batch gradient descent의 경우, cost 값이 완만하게 내려가는 모습을 보여준다.
• 반면에 mini-batch gradient descent의 경우, cost 값이 오르락 내리락하지만 크게 봤을 때는 이 역시 마찬가지로 cost 값이 내려가고 있는 모습을 보여준다.
  

그렇다면 다양한 mini-batch size 에 대한 결과는 어떻게 나올까?

• 우선 mini-batch size가 만약 $m$ (전체 데이터셋의 크기) 라면 이는 batch gradient descent와 다를 게 없다. 이 경우, 아래 파란선과 같이 global minimum을 향해 올바른 방향으로 큰 스텝으로 이동할 것이다.
  • 하지만 batch gradient descent의 경우, 한 번 학습할 때마다 연산 비용이 매우 많이 든다는 단점이 있다. (시간이 오래 걸린다.)
• 반면에 만약 mini-batch size가 1이라면 이는 stochastic gradient descent에 해당한다. 아래 보라색 선과 같이 cost 값의 변동이 매우 심하며 방향 또한 왔다갔다 한다.
  • 물론 learning rate 값을 줄이면 이러한 변동을 줄일 수 있지만, stochasitc gradient descent의 경우 vectorization의 이점을 전혀 사용하지 않아 이 역시 마찬가지로 (전체 관점에서) 시간이 오래 걸린다는 단점이 존재한다.
• 따라서 이 둘을 보완한 mini-batch gradient descent를 적용하면, 아래 초록선과 같이 적당히 올바른 방향으로 적당한 스텝으로 이동하는 모습을 보여준다.
  • mini-batch gradient descent의 경우 vectorization의 이점도 있으며 데이터셋의 크기가 작아 연산 속도도 빠르다는 이점이 있다. (즉, 학습 속도가 빠르다.)
    

따라서 mini-batch size 에 대한 조언은 다음과 같다.

• 만약 데이터셋의 크기가 작다면 (ex. $m\le2000$) batch gradient descent를 적용한다.
• 이 외에는 일반적으로 mini-batch gradient descent를 적용하며, 그 크기는 보통 2의 지수($2^n$)로 설정한다. (보통은 $2^{10}$을 많이 한다.)
• 또한 중요한 점으로, 리소스(CPU/GPU)에 따라 적당한 mini-batch size를 설정해야 한다.
  

---

다음으로 Exponentialy weighted (moving) averages 에 대해서 알아보자.
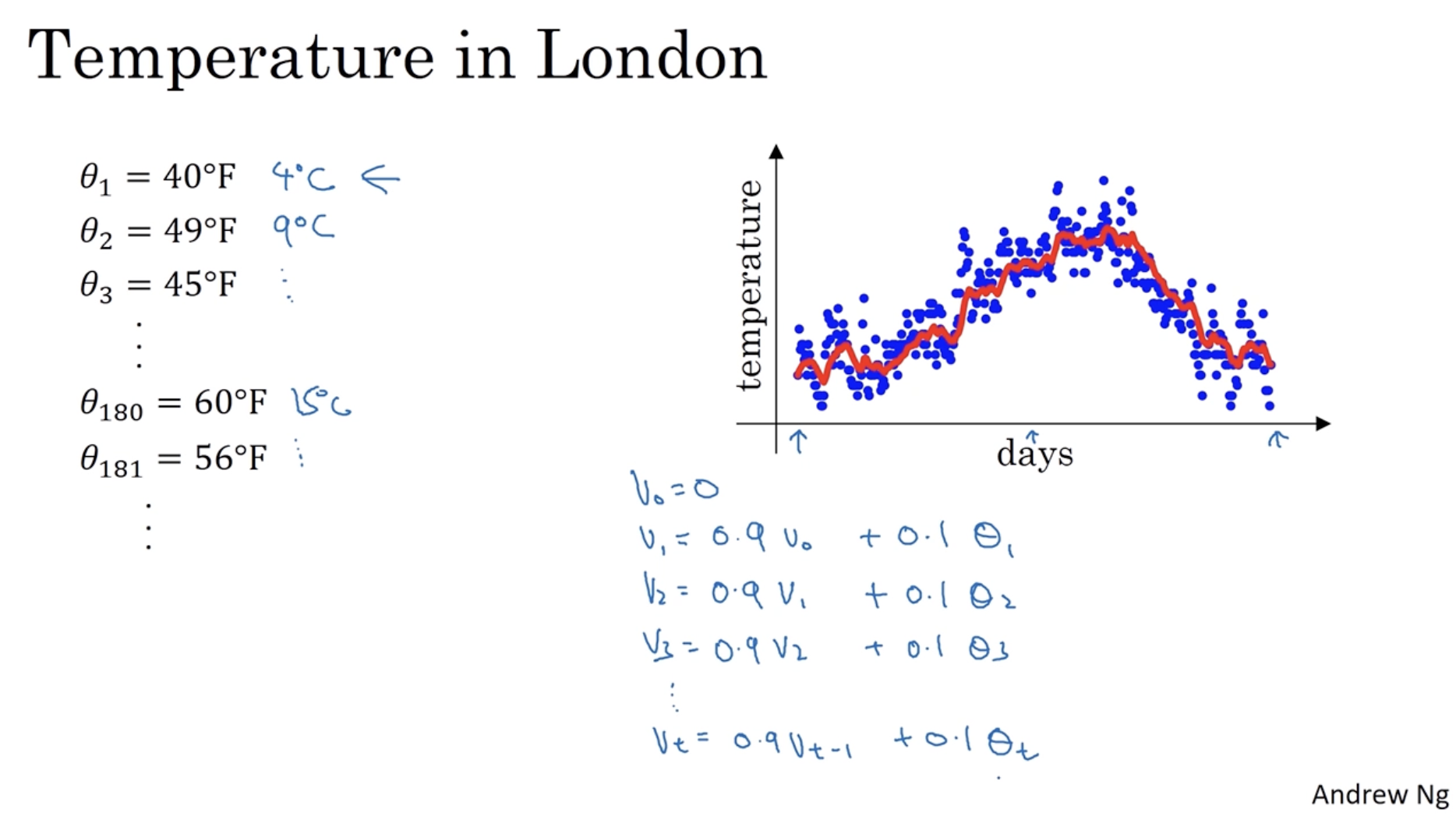
우선 아래 $\theta$는 365일 동안의 런던 기온을 나타낸다. (그래프에서 파란색 데이터 포인트에 해당한다.)

• 그리고 $v_t=0.9v_{t-1}+0.1\theta_{t}$ 와 같은 식을 적용하여, day $t$ 에서의 기온 값을 구한다. (그래프에서 빨간색 선에 해당한다.)
  • 즉, 전날의 값을 0.9만큼 그리고 당일의 weight를 0.1만큼 갖고 온다.
    

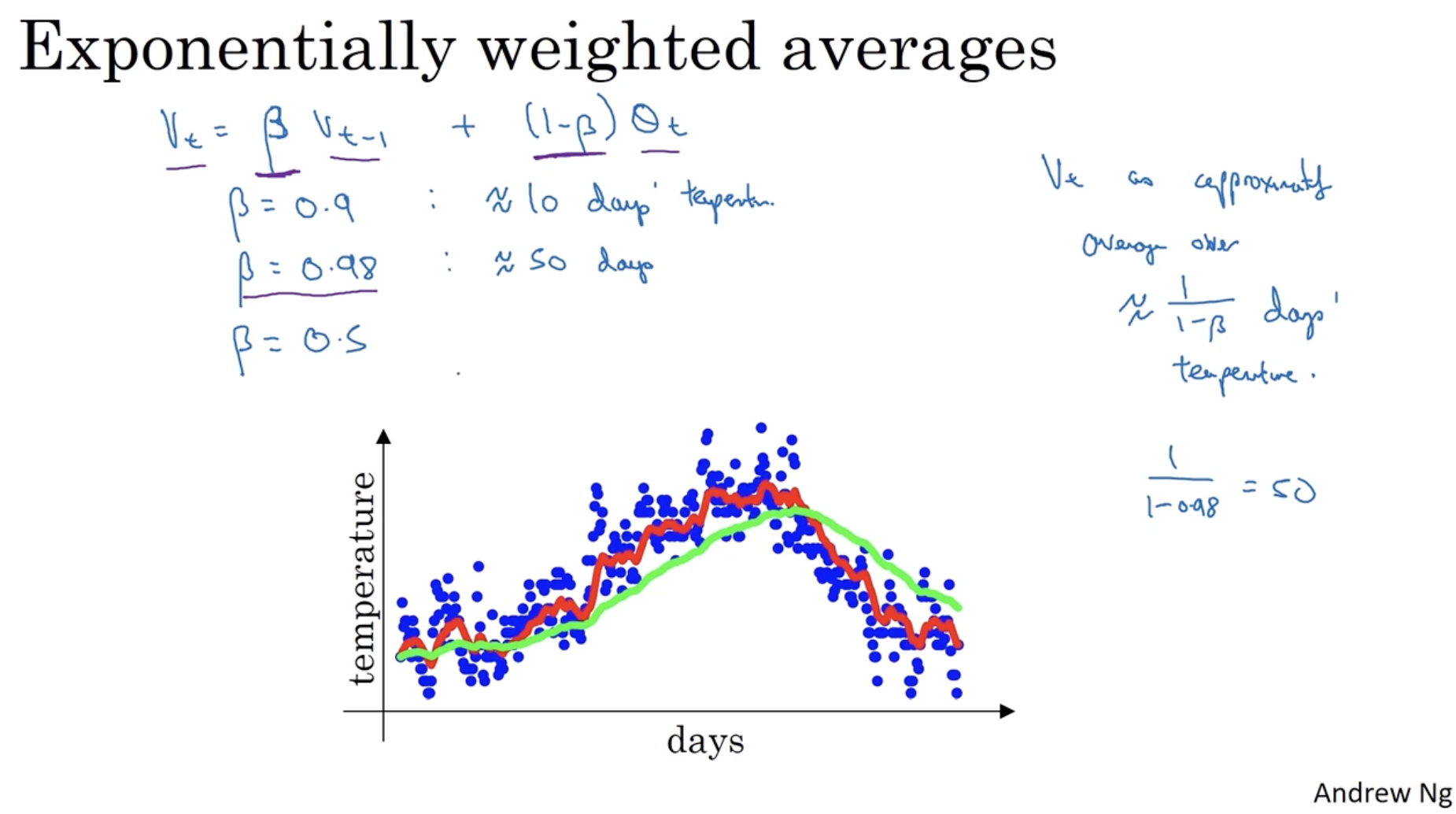
이처럼 이전 weight와 현재 weight 간의 비율을 조정하는 것을 "Exponentialy weighted (moving) averages"라고 한다. general한 식은 아래와 같다.

• $v_t=\beta v_{t-1} + (1-\beta)\theta_t$
• 따라서 $v_t$를 다음과 같이 해석할 수 있다. $v_t \approx \frac{1}{1-\beta}\text{ days' temperature.}$
• $\beta$ 값에 따라 그래프 모양이 완만해지거나 혹은 구불구불해진다.
  • 빨간선은 $\beta=0.9$, 초록선은 $\beta=0.98$.
    

---

$v_t=\beta v_{t-1}+(1-\beta)\theta_t$ 식에 의해서 다음과 같은 것들을 발견할 수 있다.
(예시에서 $\beta=0.9$)

• $v_{100}=0.1\times\theta_{100}+0.1\times0.9\times\theta_{99}+0.1\times(0.9)^2\times\theta_{98}+...$
• 그리고 각 항의 계수를 그래프로 그려 보면 우측 두 번째 그래프와 같다. (첫 번째 그래프는 $\theta_t$ 값에 대한 그래프이다.)
• 그리고 첫 번째 그래프($\theta_t$)와 두 번째 그래프(항의 계수)를 element-wise product를 하면 $v_{100}$ 값이 나오게 된다.
• 다음으로 $v_t \approx \frac{1}{1-\beta}\text{ days' temperature.}$ 가 왜 적용되는지 알아보자.
  • 우선 $(0.9)^{10}$은 10일 차의 기온 즉, $\theta_{90}$의 계수이다. 그리고 $(0.9)^{10}\approx0.35\approx\frac{1}{e}$이다.
  • 또한 $(1-\epsilon)^{1/\epsilon} \approx \frac{1}{e}$이다. (예시에서 $\epsilon=0.1=\frac{1}{10}$)
  • 만약 $\beta=0.98$ 일 경우는 어떨까?
  • $(0.98)^{x}\approx\frac{1}{e}$ 를 만족하는 $x$는 50이다. $(0.98)^{50}\approx\frac{1}{e}$
  • 그리고 이 경우 $\epsilon = 0.02=\frac{1}{50}$이다.
  • 따라서 $\epsilon = 1-\beta$ 이다.
    

exponentially weighted averages를 코드로 구현하면 우측과 같이 간단하게 구현이 가능하다.

• 이 경우 $v_\theta=0$ 으로만 할당하면 되기에, 메모리 관련 이점이 존재한다.
  

---

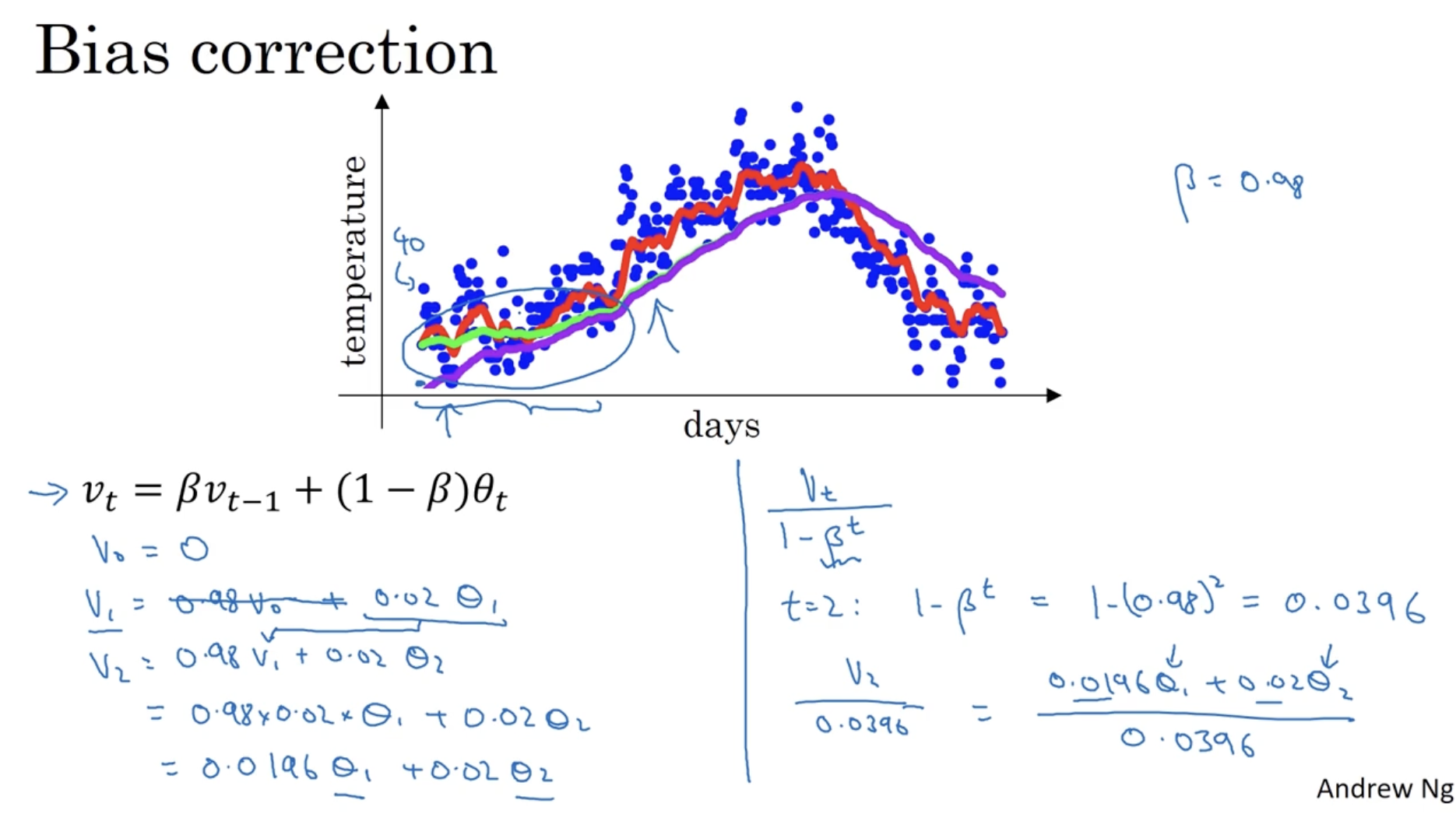
하지만 위 경우 좌측처럼 연산할 경우, 초반 $v_t$ 값들의 매우 작아질 수 있다.

• $v_0=0$
• $v_1=0.98\times v_0 + 0.02 \times \theta_1$, ...
• 위에서 $v_0=0$ 이므로 $v_1=0.02\times \theta_1$이 된다.
• 따라서 "bias correction" (bias 보정) 이 필요하다.
• 식은 간단하다. 우측과 같이 $\frac{v_t}{1-\beta^t}$ 를 적용하면 된다.
• bias correction 과정을 거치면 초반에 학습하는데 추정치 값 (온도) 을 끌어올리는 데 도움이 된다.
• 따라서 아래 그래프에서 보라색 선(no bias correction)은 초록색 선(yes bias correction)처럼 바뀔 것이다.
  

---

이제 exponentially weighted averages 개념을 gradient descent에 적용해보자.

• 아래 이미지에서 보라색 선은 learning rate가 큰 gradient descent를 의미하며, 파란선은 일반적인 gradient descent를 의미한다.
• 그리고 파란선의 움직임을 봤을 때 학습 속도가 떨어진다는 단점이 있다.
• 이를 보완하기 위해 수직의 움직임은 적게, 그리고 수평적 움직임은 크게 만들어야 하며, 이를 위해 "Momentum" 개념이 적용된다.
• 직관적으로 원리를 해석하면, 이전의 $dW,db$ 값들을 현재의 $dW,db$ 값들에 적용하여 이전의 가속도를 반영한 gradient descent를 적용한다는 의미이다.
• $vdW, vdb$ 을 통해 이전의 가속도 정보를 누적해간다.
  • $vdW=\beta\times vdW + (1-\beta)dW$
  • $vdb=\beta\times vdb + (1-\beta)db$
  • 그러고 나서 $VdW, vdb$를 gradient descent에 적용한다.
  • $W=W-\alpha \times vdw$
  • $b=b-\alpha \times vdb$
    

자세한 구현 내용은 다음과 같다.

• 현재의 mini-batch 데이터에 대해서 $dW,db$ 값을 구한 후, $vdW,vdb$ 값을 구한다.
• $vdW,vdb$ 값을 gradient descent alg.을 적용한다.
• 간혹 우측과 같이 $(1-\beta)$를 생략하는 경우도 있다. 다만 좌측처럼 생략하지 않는 것을 추천한다.
• 따라서 결론적으로 exponentially weighted averages 개념을 gradient descent alg.에 적용하는 "Momentum" 방법을 통해 더 빠른 학습 속도를 보장할 수가 있다.
  

---

gradient descent Alg.의 속도를 높이는 또 다른 방법 중 "RMSprop" (Root Mean Square prop) 방법이 있다.

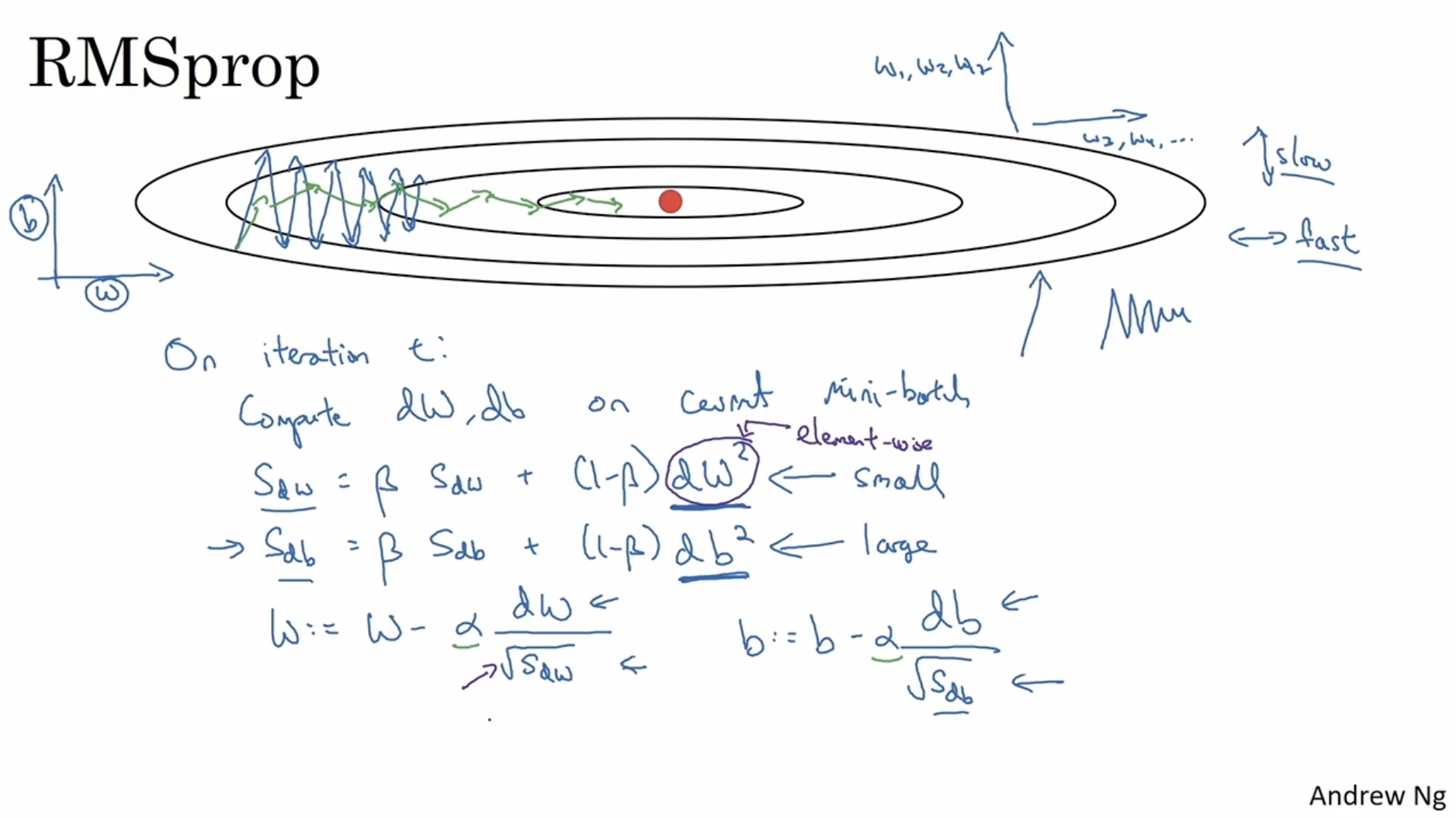
• 아래 그림에서 수직은 파라미터 $b$에 대한 경사, 수직은 파라미터 $W$에 대한 경사라고 해보자.
• 이 경우 아래 학습 곡선을 봤을 때, 수직은 천천히 움직이게 그리고 수평적 움직임은 빠르게 만들어야 학습 속도가 빨라진다.
• 이를 위해 gradient descent 수식을 다음과 같이 작성한다.
  • $sdW=\beta\times sdW + (1-\beta)\times dW^2$
  • $sdb=\beta\times sdb + (1-\beta)\times db^2$
  • $W:=W-\alpha\frac{dW}{\sqrt{sdW}}$
  • $b:=b-\alpha\frac{db}{\sqrt{sdb}}$
  • RMSprop의 원리는 다음과 같다.
  • 만약 그림과 같이 $db$의 경사가 매우 크다면 $sdb$ 값이 크게 나올 것이며, 이로 인해
    $b:=b-\alpha\frac{db}{\sqrt{sdb}}$에서 $\frac{db}{\sqrt{sdb}}$ 값이 작게 나올 것이다. 따라서 스텝 사이즈가 작아진다.
  • 반면에 $dW$의 경사가 작게 나온다면 $sdW$ 값도 작게 나올 것이고, 이로 인해
    $W:=W-\alpha\frac{dW}{\sqrt{sdW}}$에서 $\frac{dW}{\sqrt{sdW}}$ 값이 크게 나올 것이다. 따라서 스텝 사이즈가 커진다.
• 따라서 RMSprop를 적용하면 아래 녹색 선과 같이 빠른 학습 곡선을 볼 수가 있을 것이다.
  

---

그리고 가장 효율적인 optimzier로 꼽히는 "Adam" (Adaptive moment estimation) optimizer가 있다. 이는 위에서 배운 momentum 방법과 RMSprop 방법을 합친 것이다.

• 초기 $vdW, vdb, sdW, sdb$ 값은 0으로 초기화한다.
• 다음으로 mini-batch 번호인 $t$에 대해서 아래 과정을 수행한다.
  1. mini-batch $t$의 $dW,db$ 값을 구한다.
  2. $vdW=\beta_1 vdW + (1-\beta_1)dW, vdb=\beta_1 vdb + (1-\beta_1)db$ 수식을 통해 momentum 값을 구한다.
  3. $sdW=\beta_2 sdW + (1- \beta_2){dW}^2, sdb=\beta_2 sdb + (1- \beta_2){db}^2$ 수식을 통해 RMSprop 값을 구한다.
  4. ${vdW}^{correct}=\frac{vdW}{1-{(\beta_1)^t}}, {vdb}^{correct}=\frac{vdb}{1-{(\beta_1)^t}}$ 수식과
     ${sdW}^{correct}=\frac{sdW}{1-{(\beta_2)^t}}, {sdb}^{correct}=\frac{sdb}{1-{(\beta_2)^t}}$ 수식을 이용하여 bias correction을 적용한다.
  5. $W := W + \alpha\frac{{vdW}^{correct}}{\sqrt{sdW}+\epsilon}, b := b + \alpha\frac{{vdb}^{correct}}{\sqrt{sdb}+\epsilon}$ 수식을 통해 gradient descent alg.을 적용한다.
     

Adam optimizer의 하이퍼파라미터는 다음과 같다.

• $\alpha$ : learning rate, 과정에 따른 튜닝 필요.
• $\beta_1$ : 0.9, $dW,db$에 대해, momentum을 조절하는 하이퍼파라미터. (최대 몇 $t$ 전의 mini-batch 데이터까지의 모멘텀을 사용할지 결정)
• $\beta_2$ : 0.999, ${dW}^2,{db}^2$에 대해, RMSprop을 조절하는 하이퍼파라미터.
• $\epsilon$ : $10^{-8}$, RMSprop 에서 noise를 고려하는 하이퍼파라미터. 일반적으로 $10^{-8}$로 씀.
  

---

다음으로 Learning rate decay 개념에 대해서 알아보자.

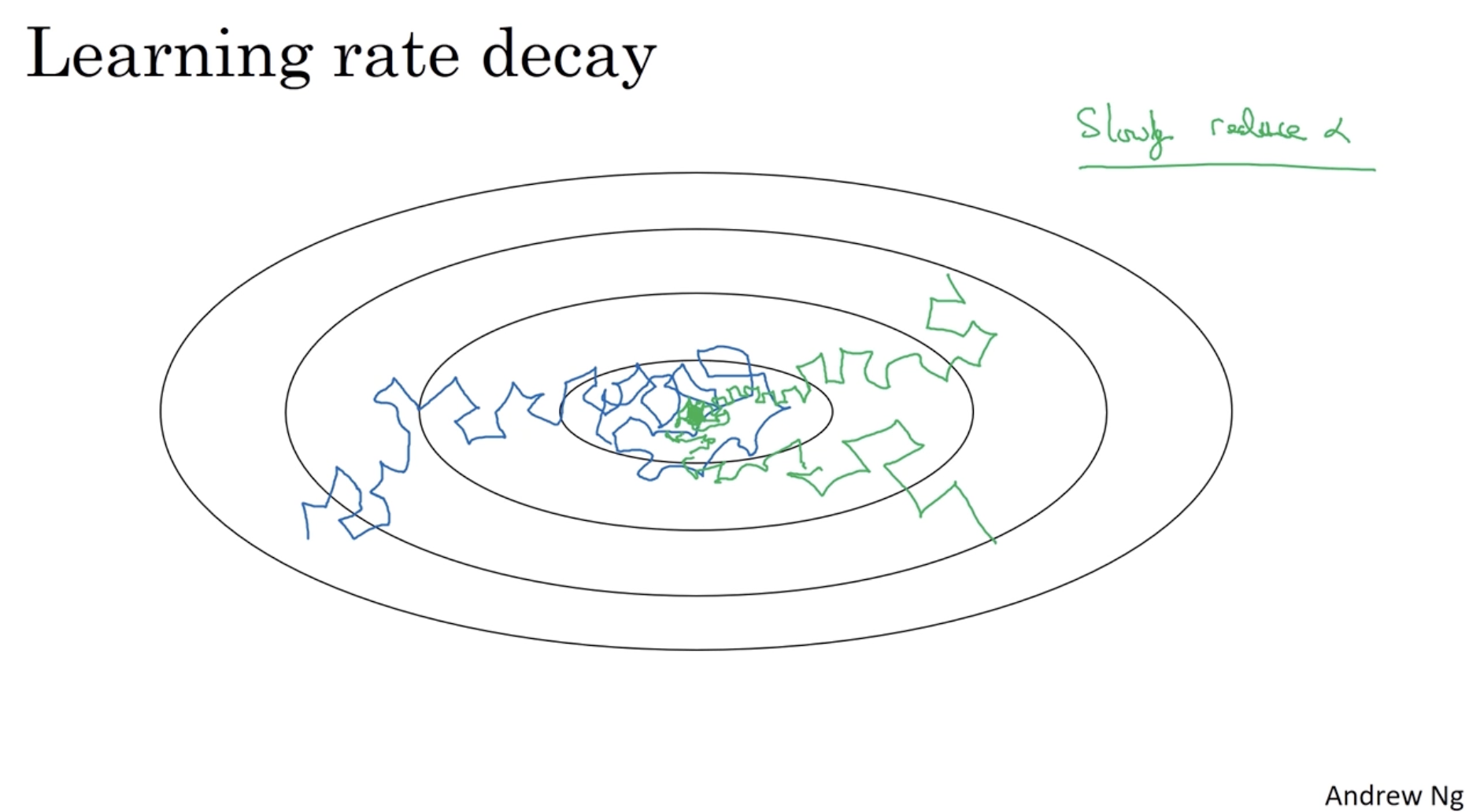
• 아래 이미지와 같이 mini-batch gradient descent의 경우 global optima에 가까워질수록 정확히 가지 못하고 주변을 배회하게 된다.
• 따라서 이를 위해 global optima에 가까워지면 (학습 수가 많아지면) learning rate를 낮춰서 step size를 낮출 필요가 있다.
• 이 방법이 learning rate decay다.
  

직관적으로 이를 구현하면 아래와 같다.

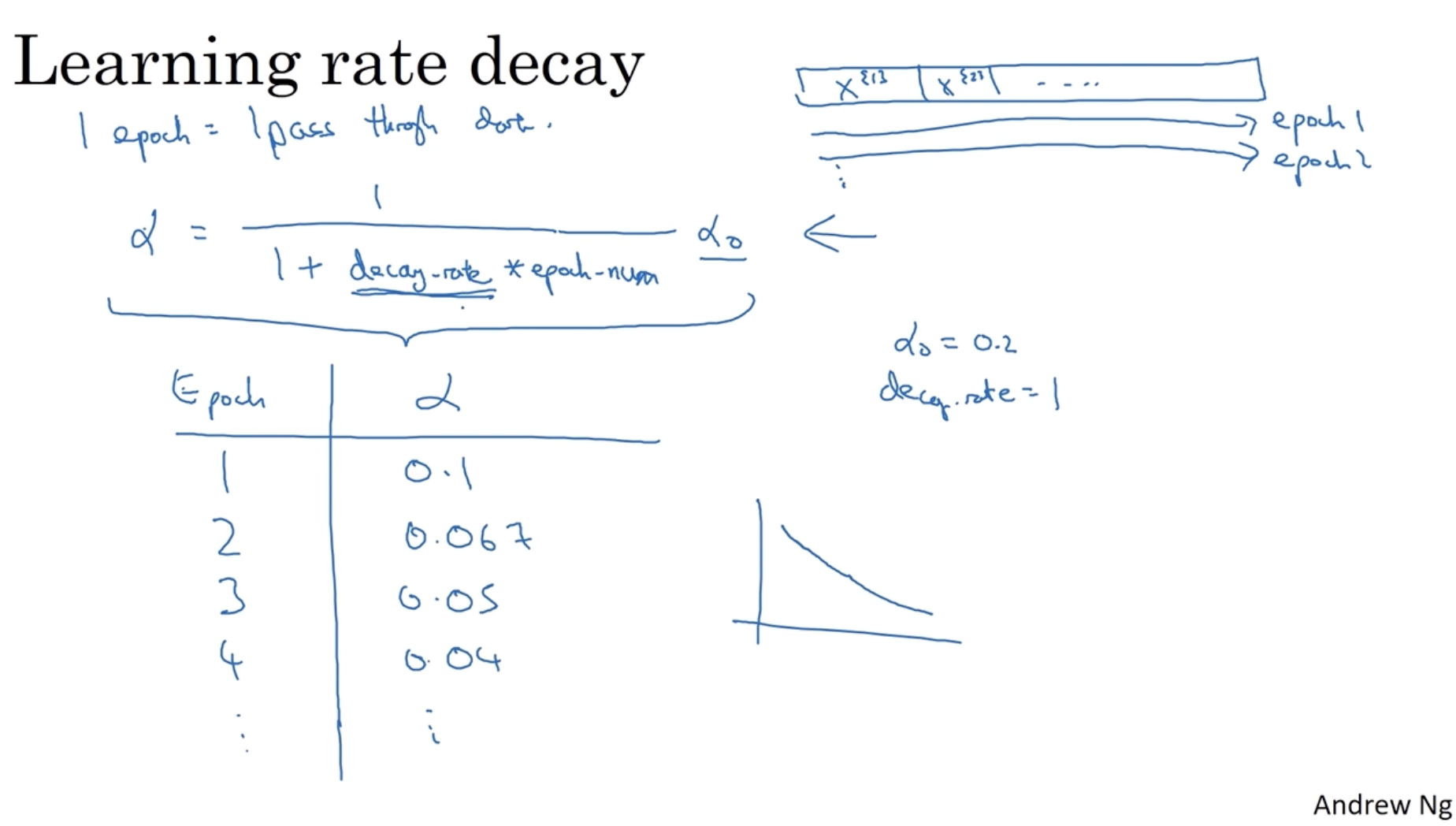
• 우선 "epoch"이라는 개념을 정의해야 하는데, "epoch"은 모든 train set에 대하여 학습을 하는 단위이다. 예를 들어 epoch=2 라면 이는 모든 train set에 대하여 2번 학습을 한다는 의미이다. 따라서 epoch 수에 따라 (혹은 mini-batch 번호에 따라) learning rate를 조절한다.
• 이제 epoch 수에 따른 learning rate decay 방법을 알아보자.
  • 수식은 다음과 같다. $\alpha = \frac{1}{1+\text{decay\_rate}\times\text{\# epochs}}\times \alpha_0$
  • 예를 들어 decay_rate가 1, $\alpha_0$이 0.2라고 가정해보자.
  • 아래와 같이 epochs 수가 늘어날 수록 learning rate 값이 작아지는 것을 확인할 수 있다. (그래프로 그리면 오른쪽과 같다.)
    

그리고 위와 같은 learning rate decay 방법뿐만 아니라 아래와 같이 다양한 learning rate decay 방법들이 있다.

• $\alpha={0.95}^{epochs}\times\alpha_0$ : exponentially decay.
• $\alpha=\frac{k}{\sqrt{epochs}}\times\alpha_0$
• $\alpha=\frac{k}{\sqrt{t}}\times\alpha_0$ (epochs 수가 아닌 mini-batch number에 따라 learning rate를 조정)
• 그리고 어떤 learning rate decay를 적용할지는 manual하게 정해야 한다.
  

---

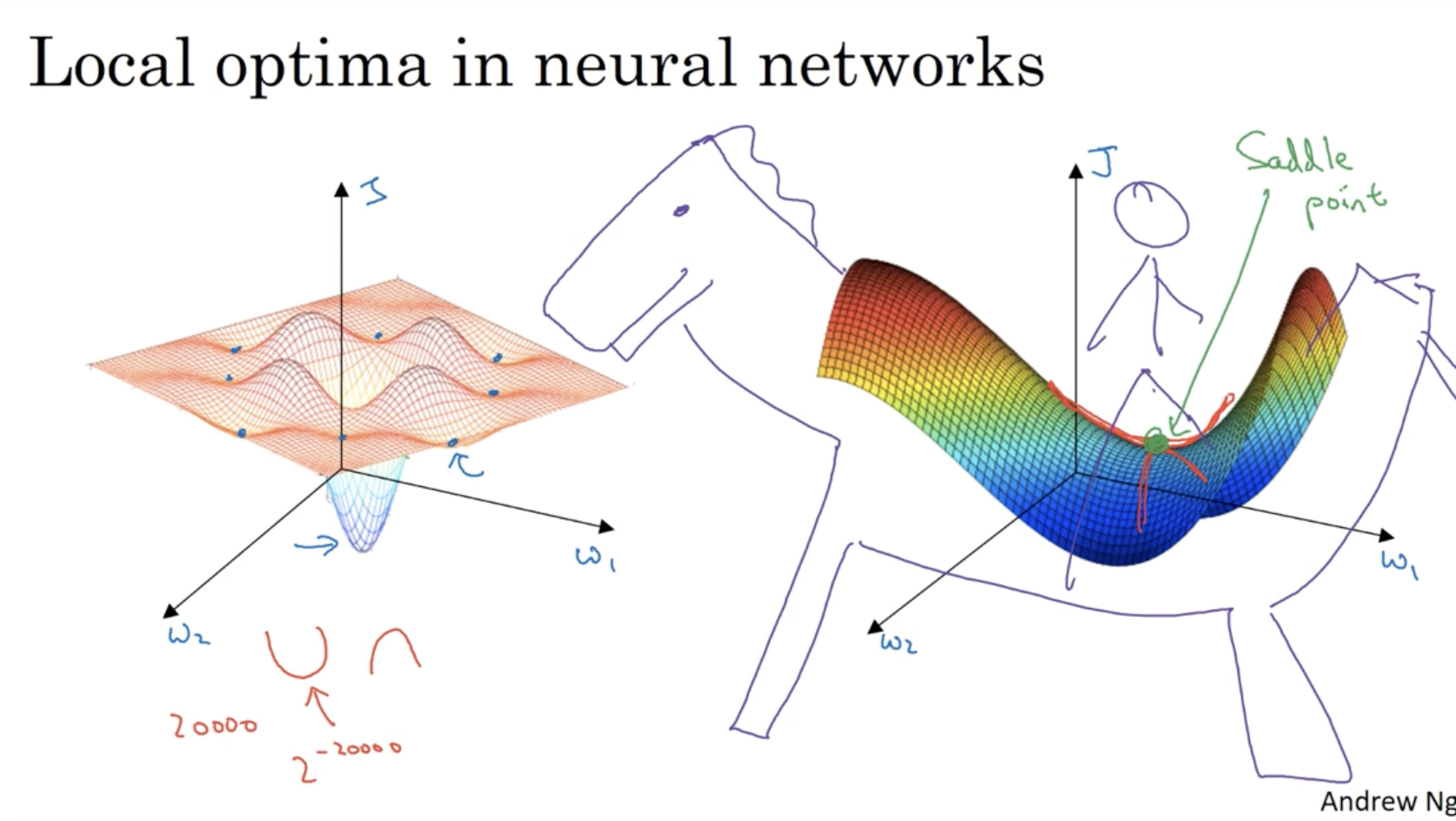
gradient descent alg.을 적용할 때 차원이 높아질 수록 좌측과 같이 다양한 local optima가 존재한다. 그리고 우리는 우측과 같이 global optima를 찾아야 한다.

• 마치 말의 안장(saddle) 부분에 global optima가 존재한다고 볼 수 있어, global optima를 saddle point라고도 부른다.
  

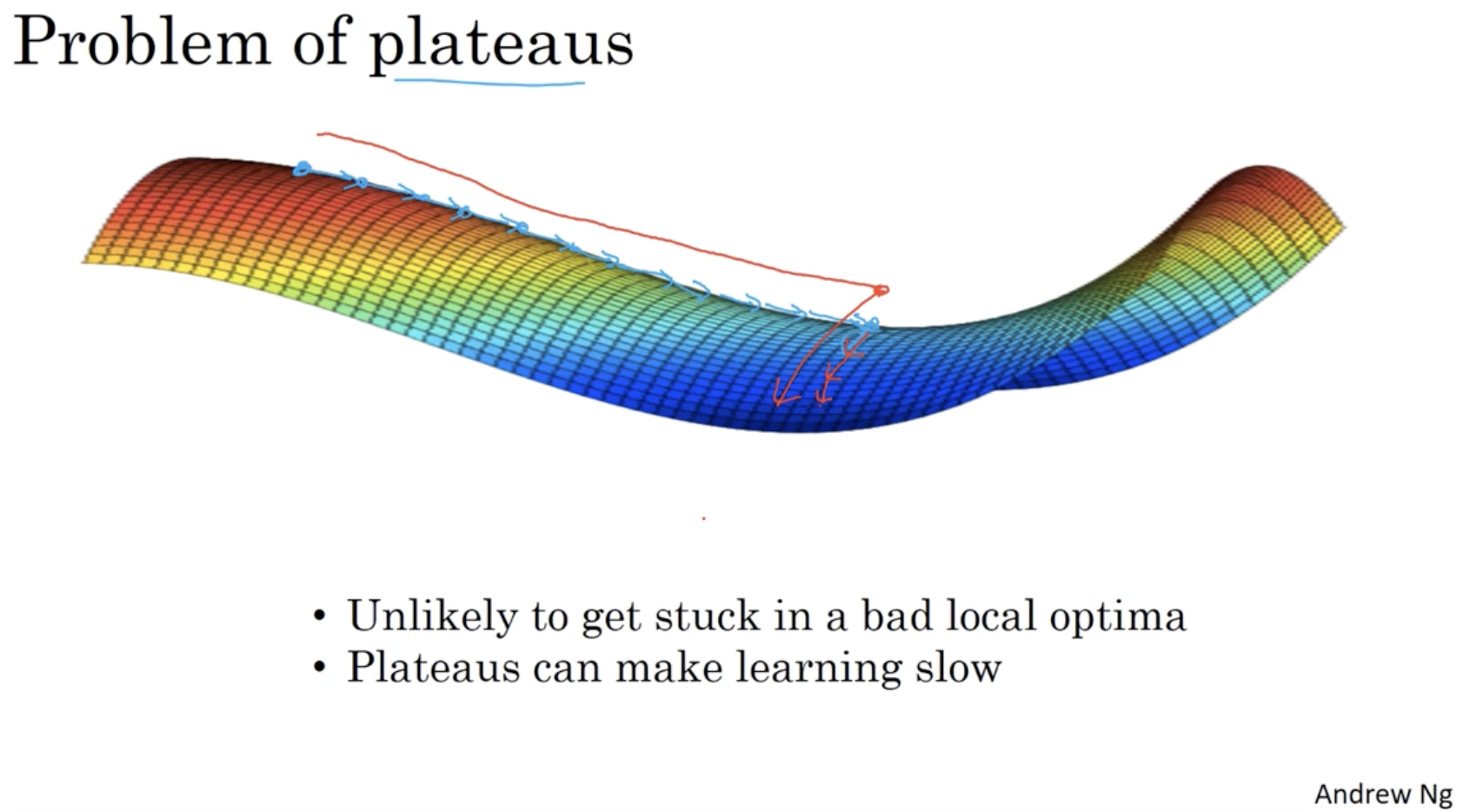
또 다른 문제로 plateaus 문제가 있다.

• 이 경우 아래 그림과 같이 global opimta에 도달하는 데 시간이 매우 오래 걸린다.
• 그리고 이때 Adam optimzier 등을 활용하면 gradient descent에 가속도가 붙어 더 빨리 학습이 가능할 것이다.