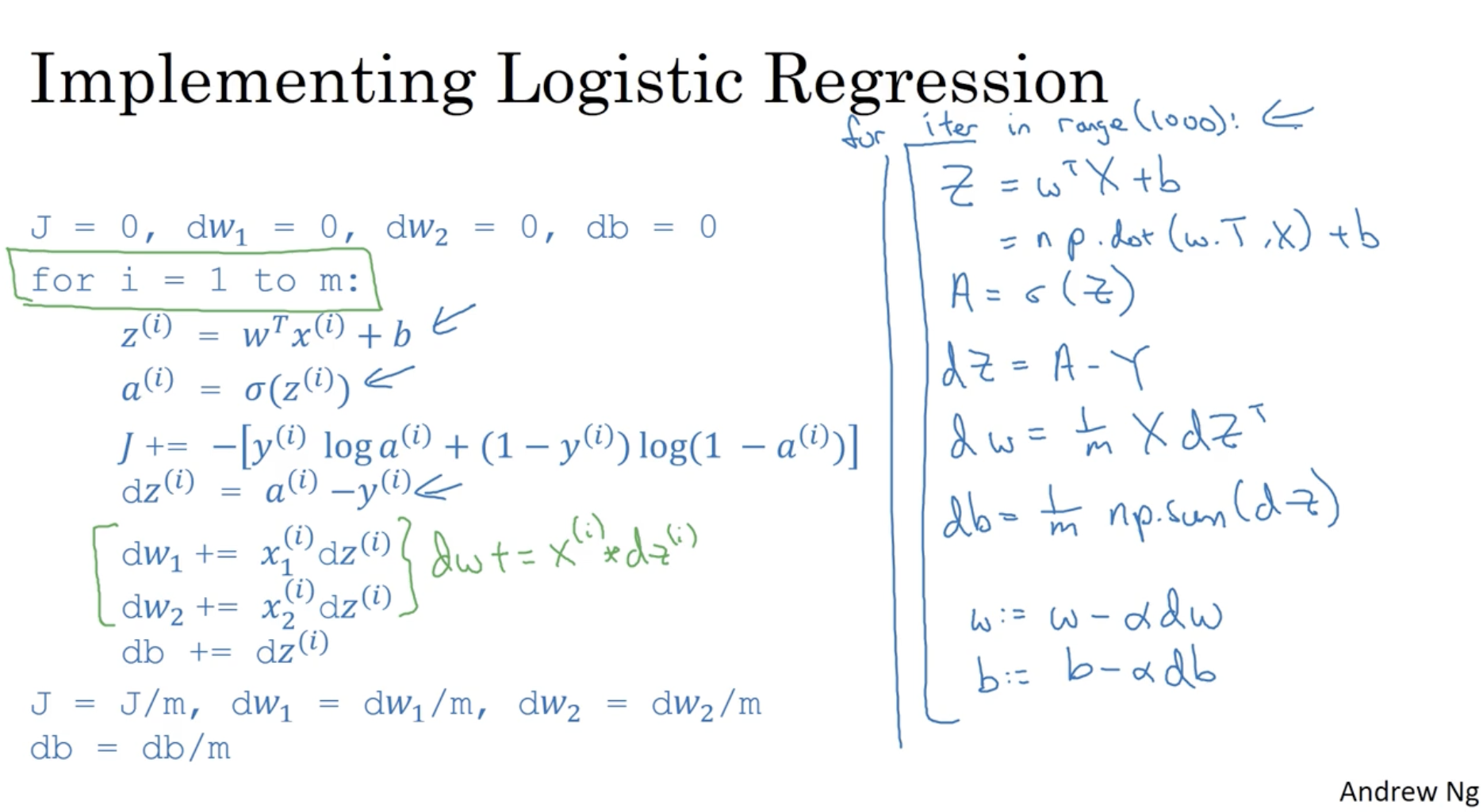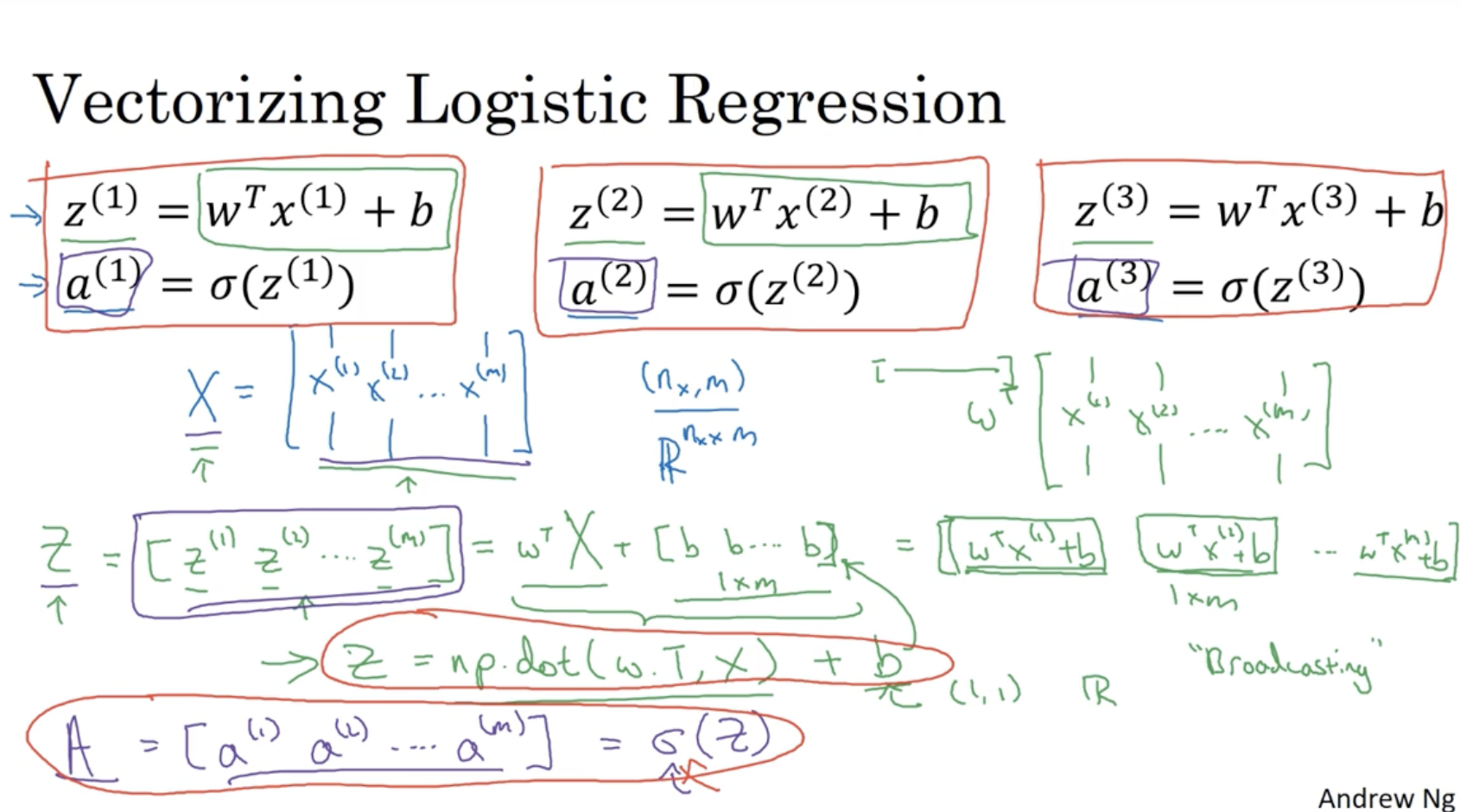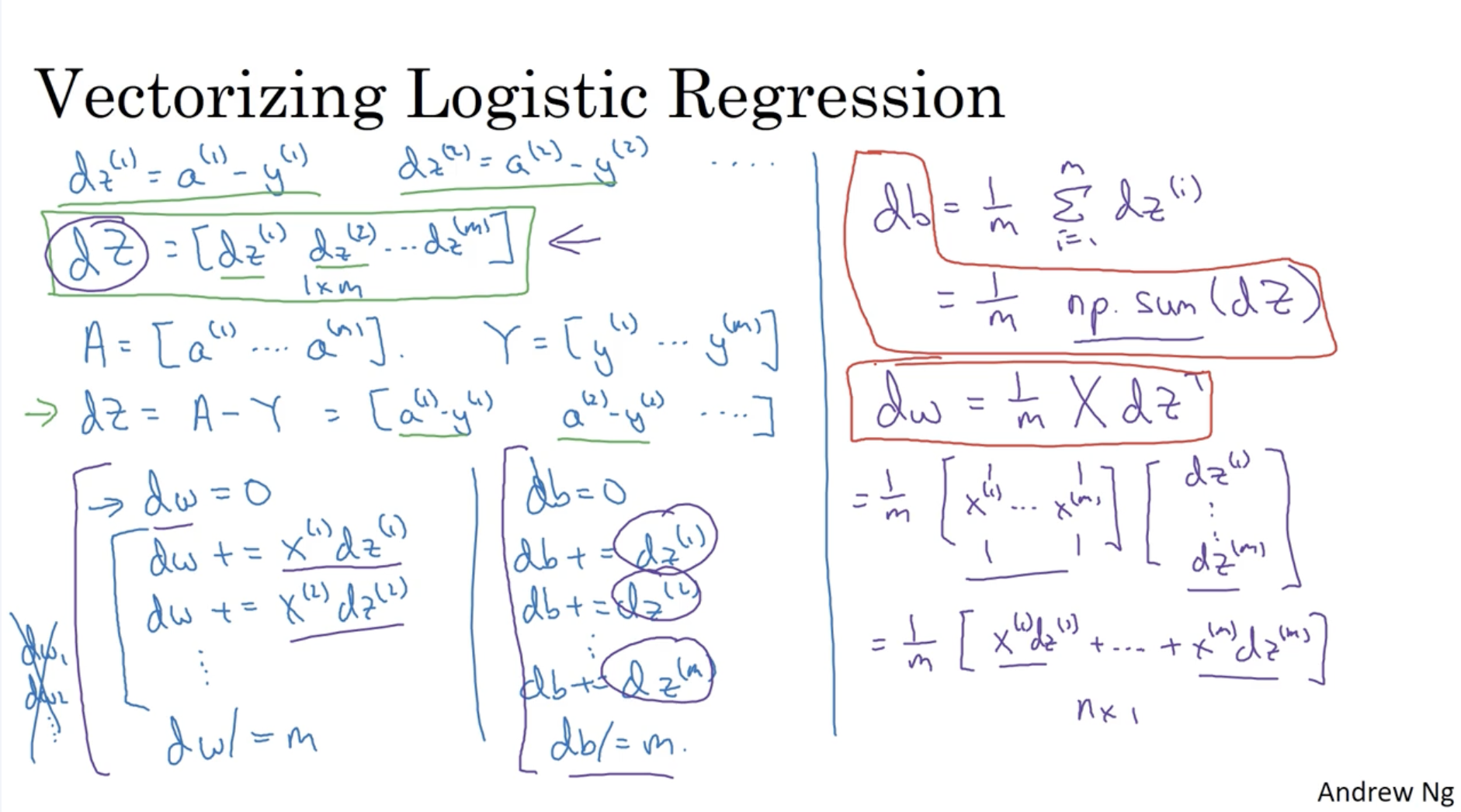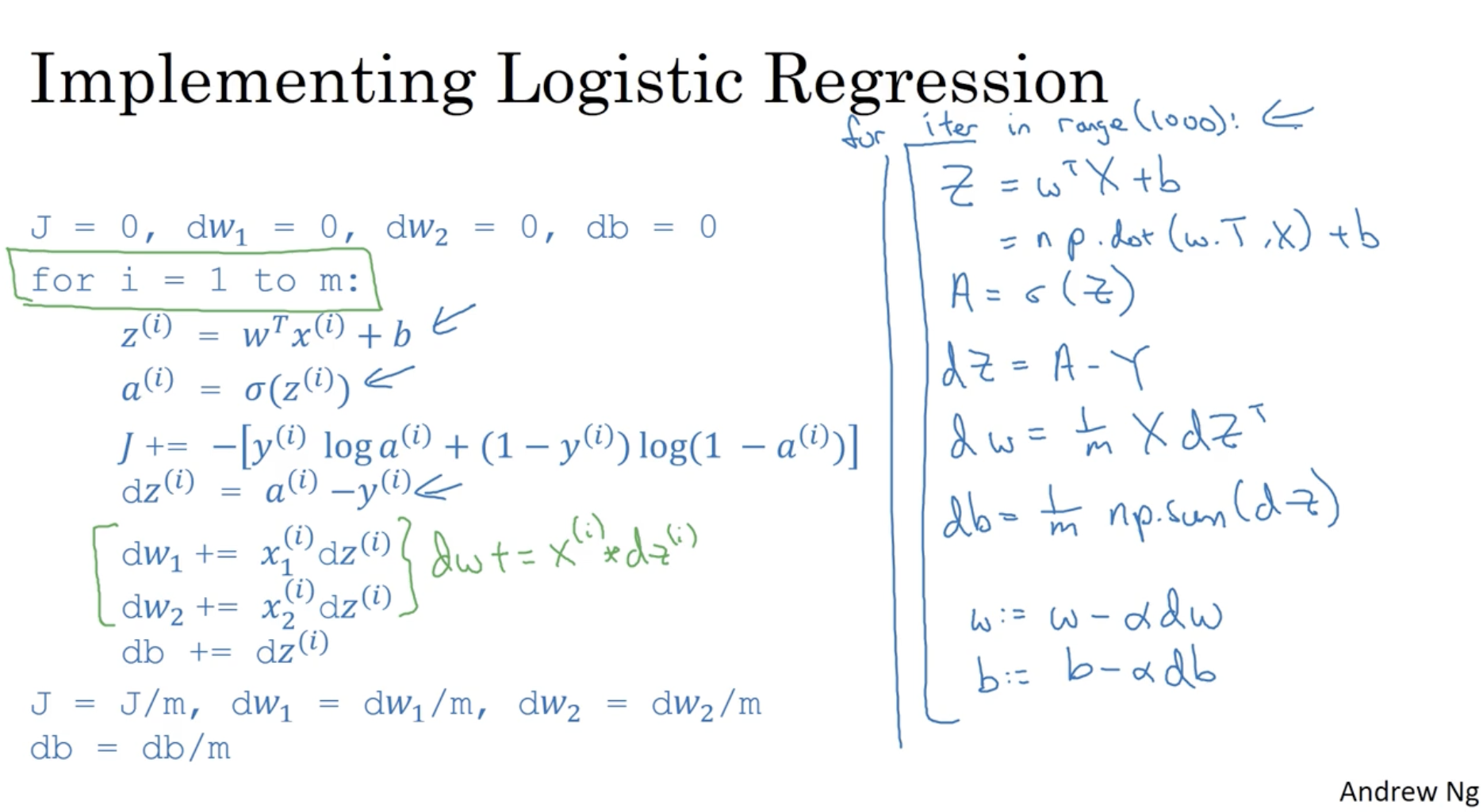[딥러닝] Neural Networks and Deep Learning Week 2

출처 : https://www.coursera.org/specializations/deep-learning

Neural Networks를 배우기 전에 기초 개념을 먼저 배운다.
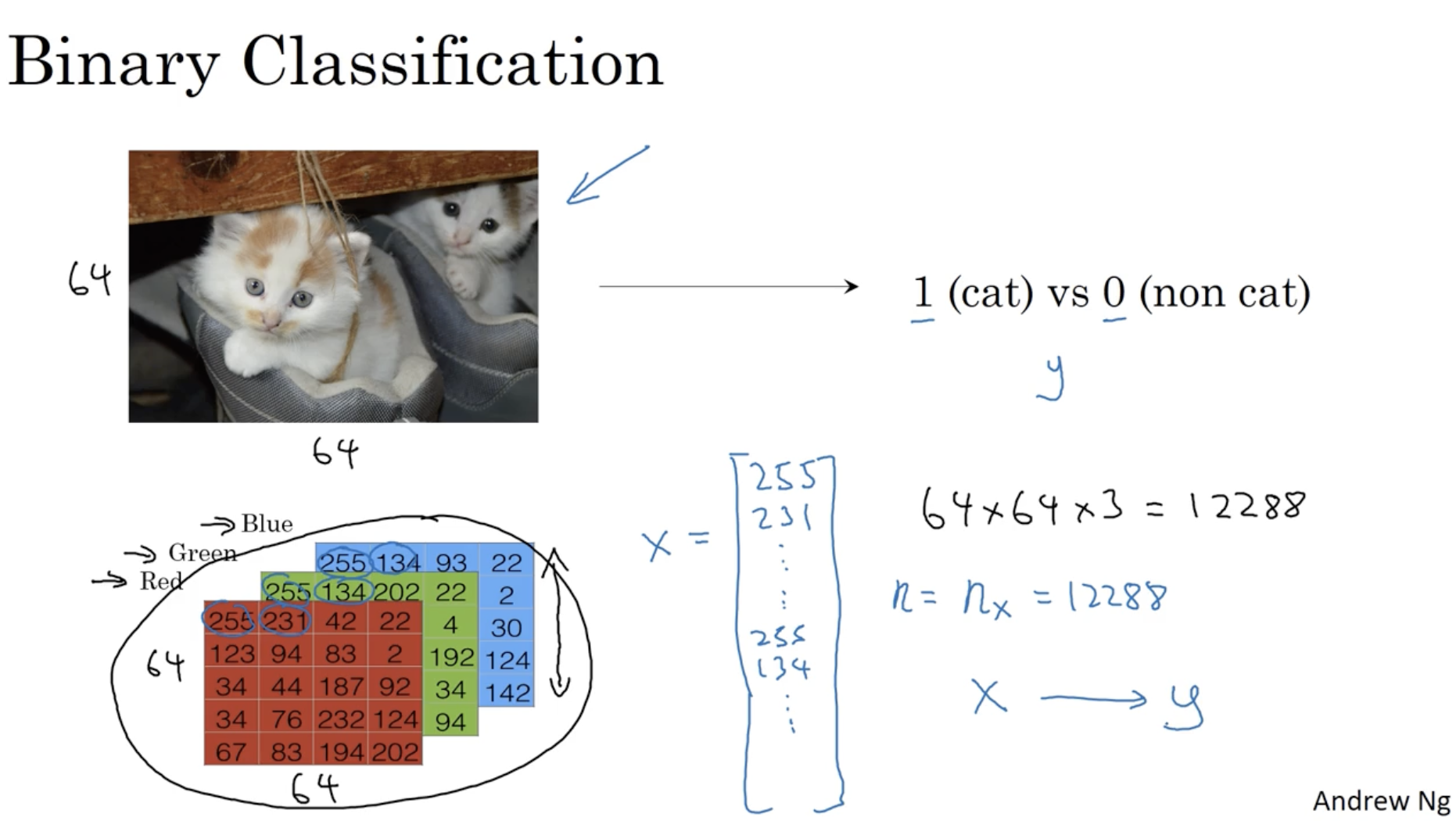
아래는 binary classification($y=1$ or $y=0$)에 대한 예시이다.

• 아래와 같이 이미지 데이터 ($64 \times 64$ pixels)가 들어 왔을 때, 이 이미지가 고양이인지($y=1$) 아닌지($y=0$)를 분류한다.
• 이미지 데이터를 vectorization하기 위해, 이미지의 각 픽셀에 해당하는 RGB 값들을 하나의 벡터로 묶는다. 아래 예시의 경우, 이미지 크기는 $64 \times 64$이며 RGB에 따라 총 $64\times64\times3$의 크기를 갖는다.
• 따라서 이미지 데이터 $x$는 다음과 같이 표현할 수 있다. $x=\begin{bmatrix}255 \\ 231 \\ | \\ 255 \\ 134 \\ | \\ 255 \\ 134 \\ |\end{bmatrix}$ 위에서부터 차례대로 R, G, B로 구분한다.
• 그리고 이때 $x$의 feature 차원은 $n_x(=n)$라고 표기하며,
  예시의 경우 $n_x=64\times64\times3=12288$이다.
  

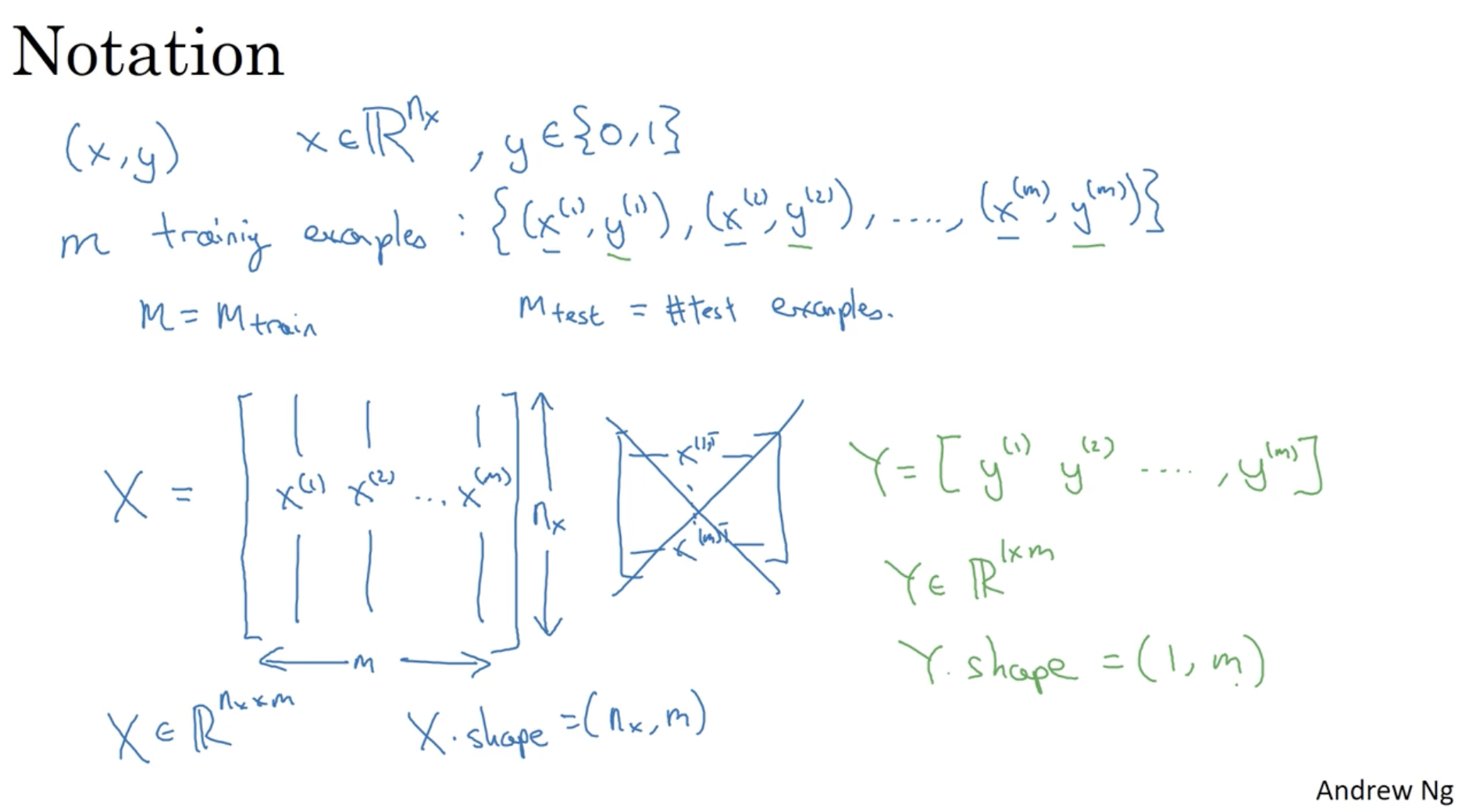
notation을 정리하면 다음과 같다.

• $(x, y)$ : 입력 데이터 $x\in \mathbb{R}^{n_x}$, 결과 데이터 $y=\{0,1\}$
• $m$ : 데이터셋의 크기. ex. $\{(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)}), ...,(x^{(m)},y^{(m)})\}$
• $M(=M_{train})$ : 학습 데이터셋의 크기
• $M_{test}$ : 테스트 데이터셋의 크기
• $X$ : 입력 데이터 $x^{(i)}(i=1,2,...,m)$의 행렬
  • $X=\begin{bmatrix}| & | & ... & | \\ x^{(1)} & x^{(2)} & ... & x^{(m)} \\ | & | & ... & | \\ \end{bmatrix} \in \mathbb{R}^{n_x\times m}$ (일반적으로 딥러닝에서는 ${x^{(1)}}^T$은 사용하지 않는다.)
  • Python에서는 $X$의 차원을 다음과 같이 표기하기도 한다. $X.shape=(n_x,m)$
• $Y$ : 결과 데이터 $y^{(i)}(i=1,2,...,m)$의 행렬
  • $Y=\begin{bmatrix}y^{(1)} & y^{(2)} & ... & y^{(m)}\end{bmatrix} \in \mathbb{R}^{1\times m}$
  • $Y.shape=(1,m)$
    

다음은 logistic regression에 대한 내용이다.

• 입력 데이터 $x$가 주어졌을 때, $y=1$일 확률을 구하는 것이 목적이다. $\hat y=P(y=1|x)$
• $x^{(i)}$의 차원은 $\mathbb{R}^{n_x}$이다.
• $x$의 각 feature의 weight를 조절하는 벡터 $w$의 차원은 $\mathbb{R}^{n_x}$이다. 그리고 bias $b$는 real number이다.
  • $w \in \mathbb{R}^{n_x}$, $b \in \mathbb{R}$
  • 예전 강의에서 $\hat y=\theta^Tx$와 같이 사용한 적이 있는데, 이는 $\hat y=w^Tx+b$와 같다. 다만 현재는 $w$와 $b$를 구분해서 하는 방법을 선호하기 때문에 $\theta$는 사용하지 않는다.
• $\hat y=P(y=1|x)$을 구할 때 일반적인 linear regression 모델을 적용하면, 값의 범위가 0~1을 벗어난다. 따라서 sigmoid 함수를 적용하여 값의 범위가 (0, 1)이 되도록 만든다.
  • $\hat y = \sigma(w^Tx+b)=\frac{1}{1+e^{-(w^Tx+b)}}$
    

다음은 Logistic regression의 cost function과 loss (error) function에 대한 내용이다.

• $\hat y = \sigma(w^Tx+b)=\frac{1}{1+e^{-(w^Tx+b)}}$
• 만약 $x^{(i)}$가 주어졌을 때 우리는 다음과 같이 학습하기를 원한다. $\hat y^{(i)} \approx y^{(i)}$.
• logistic regression의 Loss function $L(\hat y,y)$은 다음과 같이 정의한다.
  $L(\hat y, y)=-(y \ log \ \hat y +(1-y)log(1-\hat y) )$
  • $y$가 1일 때, $L(\hat y, y)=-log \ \hat y$ 와 같이 나오며, Loss를 줄이기 위해 $\hat y$는 1로 가야한다.
  • $y$가 0일 때, $L(\hat y, y)=-(1-y)log(1-\hat y)$ 와 같이 나오며, Loss를 줄이기 위해 $\hat y$는 0으로 가야한다.
• 다음으로 Cost function은 다음과 같이 정의한다.
  $J(w,b)=\frac{1}{m}\sum_{i=1}^{m}L(\hat y^{(i)}, y^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)} \ log \ \hat y^{(i)} +(1-y^{(i)})log(1-\hat y^{(i)})]$
• 즉, $L(\hat y, y)$는 하나의 데이터에 대한 error 값을 의미하고, $J(w,b)$는 전체 데이터에 대한 평균 error 값을 의미한다.
  

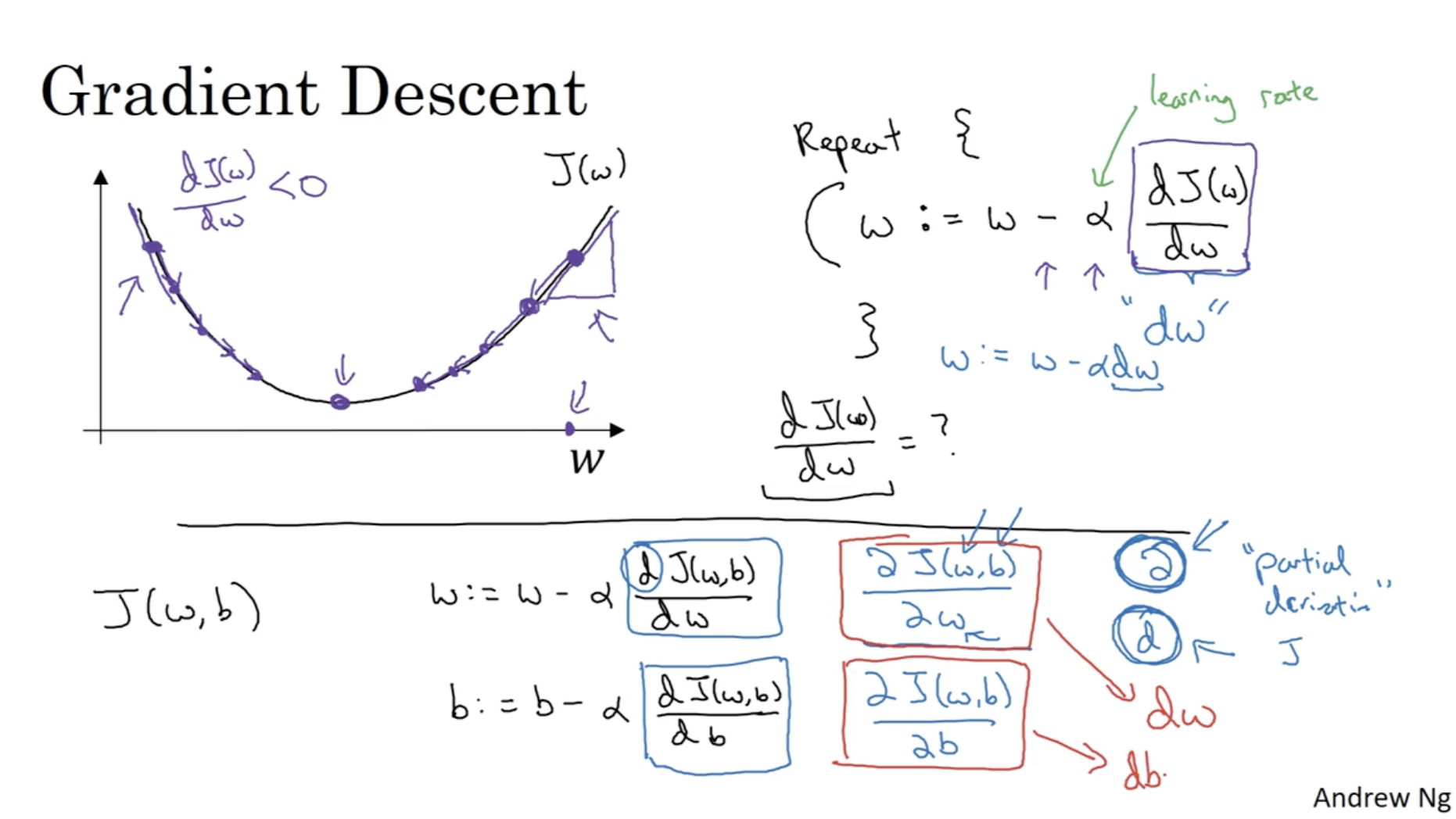
다음은 Gradient Descent에 대한 내용이다.

• 아래 그림과 같이 parameter $w, b$ 값에 따른 cost function $J(w,b)$ 값을 그려보면 convex한 함수가 나오는 것을 확인할 수 있다.
• 그리고 우리의 목적은 cost function $J(w,b)$의 값이 최소가 되는 $(w,b)$ 값을 찾는 것이다.
• 이렇게 cost function $J(w,b)$의 값이 최소가 되는 점을 "global optima(minimum)"이라고 한다.
  

이제 Gradient Descent alg.을 적용해보자.

• 아래 그래프와 같이 cost function의 global optima를 찾기 위해서 파라미터 $w$의 값은 기울기의 반대 방향으로 이동해야 한다. 따라서 $w$에 대한 gradient descent는 $w:=w-\alpha\frac{dJ(w)}{dw}$와 같이 작동한다.
• $\alpha$ : learning rate를 의미하여, 얼만큼 움직일지를 (step size를) 결정한다.
• 따라서 cost function $J(w, b)$에 대한 gradient descent alg.을 작성하면 다음과 같다.
  • $w:=w-\alpha\frac{\partial J(w,b)}{\partial w}$
  • $b:= b-\alpha\frac{\partial J(w,b)}{\partial b}$
  • 그리고 코드로 위 과정을 구현할 때, $\frac{\partial J(w,b)}{\partial w}, \frac{\partial J(w,b)}{\partial b}$은 각각 $dw,db$로 표기한다.
    

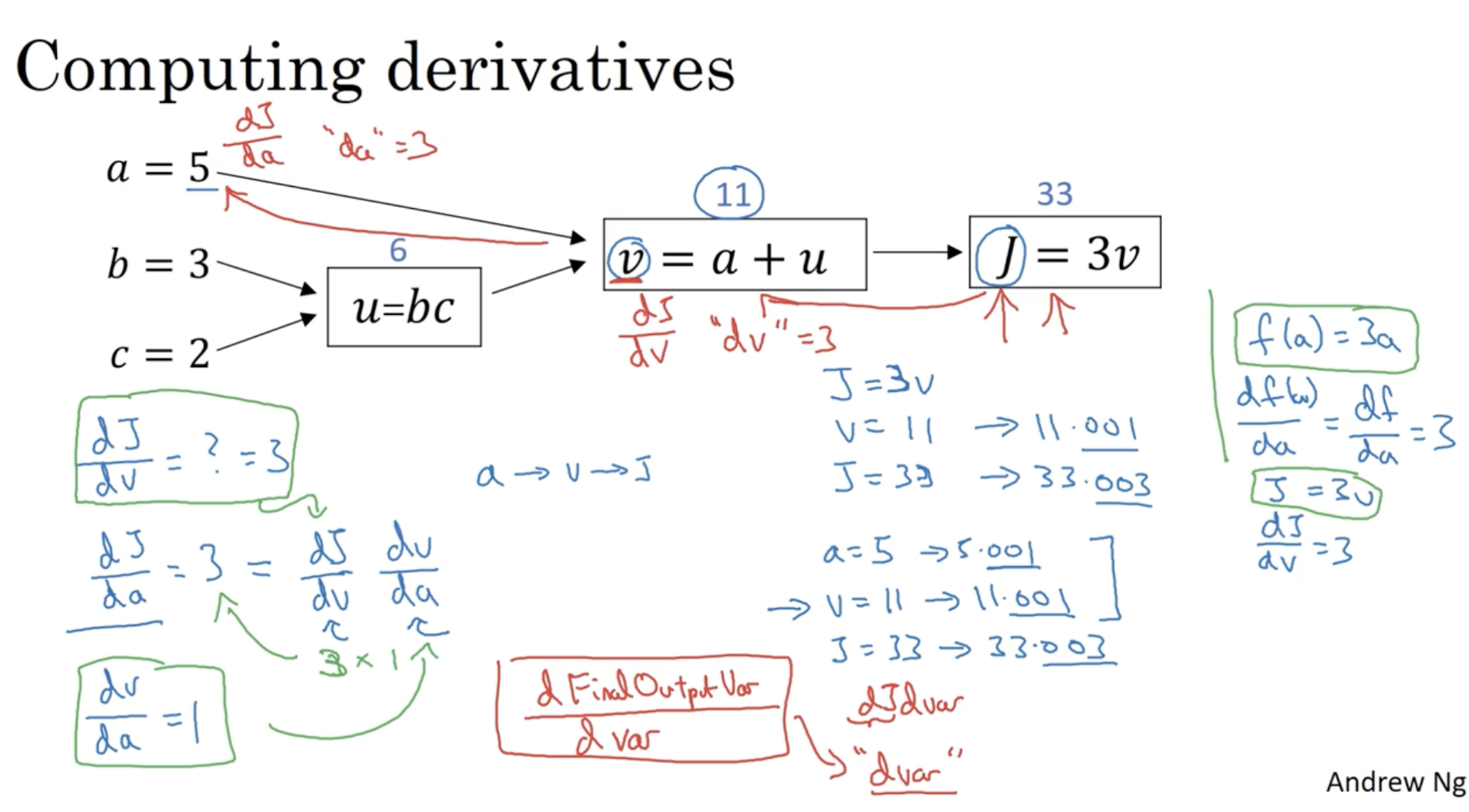
Neural Networks의 back propagation을 위해 미분값을 구하는 과정이 필요하다. 즉, 아래 예시에서 최종 output $J(a,b,c)$에 대한 입력값 $a,b,c$의 미분값 $\frac{dJ}{da},\frac{dJ}{db},\frac{dJ}{dc}$의 값이 있어야 각 feature에 대한 gradient descent alg. 적용이 가능하다.

• 아래에서 우선 $J$에 대한 $v$의 미분값을 구해보자. $\frac{dJ}{dv}=3$
• 그리고 $v$에 대한 $a$의 미분값과 $u$의 미분값을 구해보자. $\frac{dv}{da}=1, \frac{dv}{du}=1$
  • 여기서 "chain rule"에 의해 $J$에 대한 $a$의 미분값을 구할 수가 있다.
  • $\frac{dJ}{da}=\frac{dJ}{dv}\times\frac{dv}{da}=3\times1=3$ (파이썬 코드에서는 이를 "$da$"로 표기한다.)
• 다음으로 $u$에 대한 $b$의 미분값과 $c$의 미분값을 구해보자. $\frac{dv}{db}=c=2, \frac{dv}{dc}=b=3$
  • 위와 마찬가지로 chain rule에 의해 $J$에 대한 $b,c$의 미분값을 구할 수가 있다.
  • $\frac{dJ}{db}=\frac{dJ}{dv}\times\frac{dv}{db}=3\times2=6$ (파이썬 코드에서는 이를 "$db$"로 표기한다.)
  • $\frac{dJ}{dc}=\frac{dJ}{dv}\times\frac{dv}{dc}=3\times3=9$ (파이썬 코드에서는 이를 "$dc$"로 표기한다.)
• 파이썬 코드에서 $output$ 값에 대한 변수 $var$의 미분값은 "$dvar$"로 표기한다.
  

각 $dvar$에 대한 최종 결과는 아래와 같다.

그렇다면 위와 같은 방식을 logistic regression에 적용해보자.

• $z=w^Tx+b$
• $\hat y=a=\sigma(z)$
• $L(a,y)=-(y \ log \ a + (1-y)log(1-a))$
• 위 수식들을 graph 형태로 표현하면 아래와 같이 나온다. ($x$의 feature는 $x_1,x_2$ 두 개만 있다고 가정.)
  

그리고 $L(a,y)$에 대한 파라미터 $w_1,w_2,b$의 미분값 $\frac{\partial L(a,y)}{\partial w_1},\frac{\partial L(a,y)}{\partial w_2},\frac{\partial L(a,y)}{\partial b}$를 구해보자.

• 먼저 $L(a,y)$에 대한 $a$의 미분값은 다음과 같다. $\frac{\partial L(a,y)}{\partial a}=-\frac{y}{a}+\frac{1-y}{1-a}$ (= "da" in Python)
• 다음으로 $L(a,y)$에 대한 $z$의 미분값은 다음과 같다.
  $\frac{\partial L(a,y)}{\partial z}=\frac{\partial L(a,y)}{\partial a}\times\frac{\partial a}{\partial z}=(-\frac{y}{a}+\frac{1-y}{1-a})\times a(1-a)=a-y$ (= "dz" in Python)
• 그리고 $L(a,y)$에 대한 $w_1,w_2,b$의 미분값은 다음과 같다.
  • $\frac{\partial L(a,y)}{\partial w_1}=\frac{\partial L(a,y)}{\partial z}\times\frac{\partial z}{\partial w_1}=(a-y)\times x_1$ (= "dw1" in Python)
  • $\frac{\partial L(a,y)}{\partial w_2}=\frac{\partial L(a,y)}{\partial z}\times\frac{\partial z}{\partial w_2}=(a-y)\times x_2$ (= "dw2" in Python)
  • $\frac{\partial L(a,y)}{\partial b}=\frac{\partial L(a,y)}{\partial z}\times\frac{\partial z}{\partial b}=(a-y)\times 1$ (= "db" in Python)
• 따라서 위에서 구한 $\frac{dL(a,y)}{dw_1},\frac{dL(a,y)}{dw_2},\frac{dL(a,y)}{db}$ 값을 통해 gradient descent alg.을 적용하면 다음과 같다.
  • $w_1:=w_1-\alpha\times dw1$
  • $w_2:=w_2-\alpha\times dw2$
  • $b:=b-\alpha\times db$
    

위에서는 하나의 데이터에 대한 gradient descent의 과정을 살펴봤다. 다음으로 $m$개의 데이터셋에 대한 gradient descent 과정을 살펴본다.

• $J(w,b)=\frac{1}{m}\sum_{i=1}^mL(a^{(i)},y^{(i)})$
• 따라서 여러 개의 데이터에 대한 평균값을 기준으로 gradient descent를 적용하면 된다.
  • Ex. $\frac{\partial}{\partial w_1}J(w,b)=\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial w_1}L(a^{(i)},y^{(i)})=\frac{1}{m}\sum_{i=1}^m{dw1}^{(i)}$
    

코드로 구현하면 아래와 같다.

• $J,dw1,dw2,db$ 의 초기값을 0으로 세팅한다.
• $i=1 \to m$에 대하여 $J^{(i)},dw1^{(i)},dw2^{(i)},dw3^{(i)}$ 값을 구한 후, $J,dw1,dw2,db$ 에 누적한다.
• 누적된 $J,dw1,dw2,db$의 값을 $m$으로 나눠준다.
• 평균 $dw1,dw2,db$ 값을 가지고 gradient descent alg.을 적용한다.
• 하지만 위와 같은 방식으로 적용할 경우, 데이터 수 $m$ 만큼과 feature 수 $n$ 만큼 loop 문이 필요하다. 따라서 두 값이 클 경우 연산 비용이 기하급수적으로 증가할 수 있다.
• 따라서 효율적인 계산을 위해 "Vectorization" 기술이 적용될 필요가 있다.
  

좌측은 vectorization을 적용하지 않은 python 코드를 의미하고, 우측은 vectorization을 적용한 Python 코드를 의미한다.

• 좌측의 경우 일일이 $z$ 값을 갱신하지만, 우측은 $np.dot()$ 연산을 통해 한번에 $z$값을 구한다.
  

위를 직접 코드로 실행해보면 다음과 같은 결과가 나온다.

• 두 과정 모두 $z$ 값에는 변화가 없지만 (매우 매우 작은 차이만 존재하지만), 실행 속도는 vectorization을 적용한 버전이 훨씬 더 빠르다는 것을 확인할 수 있다.
  
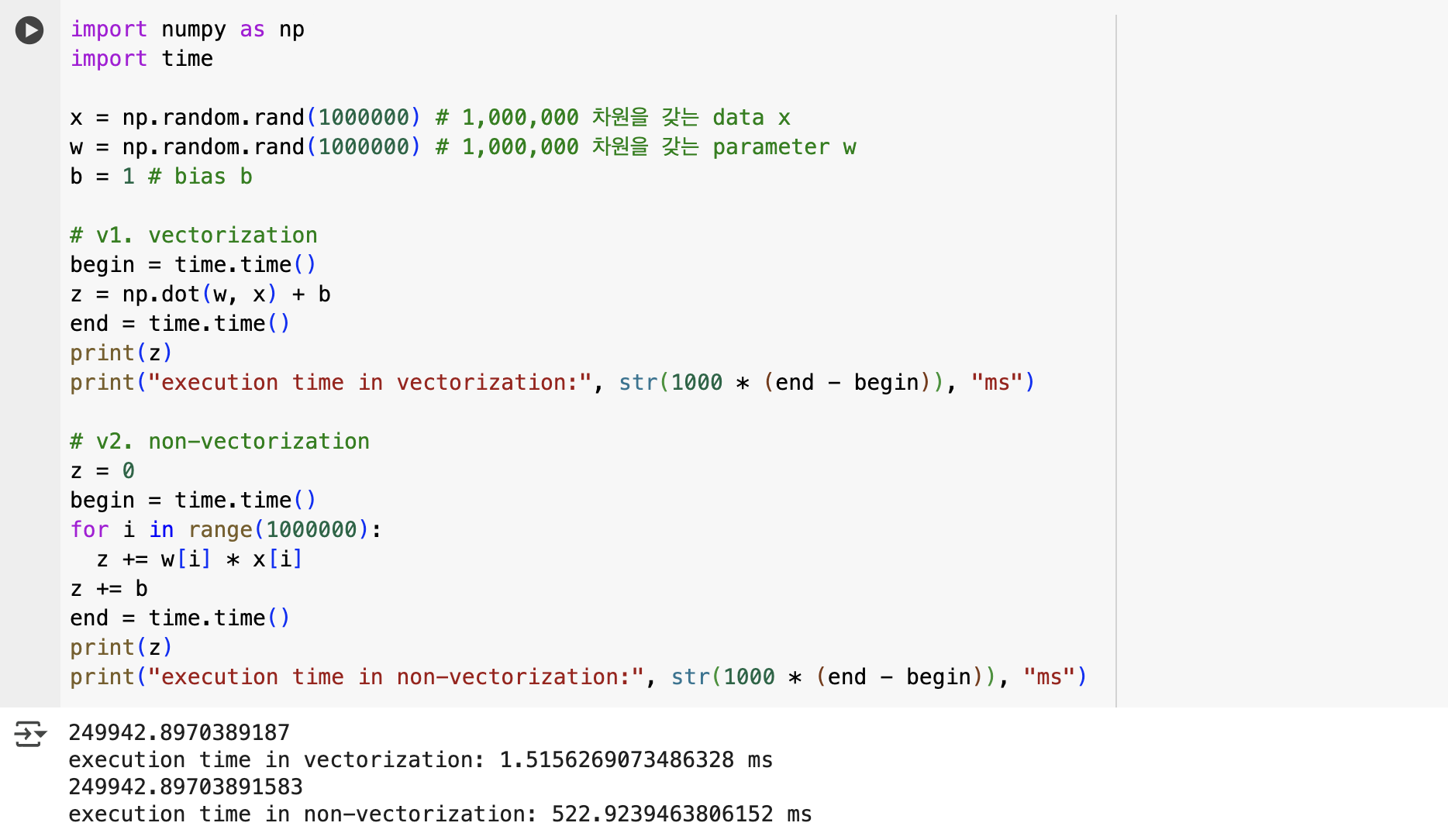
• 이처럼 컴퓨터에서 vectorization이 빠르고 가능한 이유는 CPU, GPU 등은 SIMD (single instruction multiple data) 명령어가 가능한 multi programming을 제공하기 때문이다. 그리고 특히 GPU는 병렬 처리 측면에서 강한 이점을 보여준다.

따라서 되도록이면 Neural Network를 구현할 때, 좌측과 같은 for-loop 대신, 우측과 같이 vectorization을 적용하는 것이 좋다.

또한 numpy는 다양한 기능을 제공하고 있어, 아래 그림과 같이 $v$ 벡터에 exp 연산이 적용된 $u$ 벡터를 구하고 싶다면, 좌측과 같이 for-loop을 통해 일일이 값을 넣는 것이 아니라,
우측처럼 u=np.exp(v) 코드를 사용하여 한번에 할 수 있다.

• 뿐만 아니라 numpy에서는 np.log(v), np.abs(v), np.maximum(v, 0), v**2, 1/v 등 다양한 기능을 제공하고 있다.
  

따라서 이전의 logistic regression 중 미분값을 구하는 과정에 vectorization을 적용하면 간단하게 dw = np.zeros((n, 1)), dw += x[i]dz[i]와 같이 구현할 수 있다.

그렇다면 $m$개의 데이터셋에 대한 각 $z^{(i)}, a^{(i)}$의 값은 어떻게 vectorization을 활용하여 구할 수가 있을까?

• 우선 행렬 $X$를 다음과 같이 정의한다. $X=\begin{bmatrix}| & | & ... & | \\ x^{(1)} & x^{(2)} & ... & x^{(m)} \\ | & | & ... & | \\ \end{bmatrix} \in \mathbb{R}^{n_{x}\times m}$
• 그리고 벡터 $w$는 다음과 같다. $w=\begin{bmatrix}w_1 \\ w_2 \\ ... \\ w_{n_x}\end{bmatrix} \in \mathbb{R}^{n_x \times 1}$
• 따라서 $z^{(i)}$의 값들의 집합 행렬 $Z \in \mathbb{R}^{1 \times m}$는 다음과 같다. $Z=w^TX+\begin{bmatrix}b & b & ... & b\end{bmatrix}$
• 위 vectorization을 python 코드로 적용하면 다음과 같다.
  • Z = np.dot(w.T, X) + b (여기서 $b\in \mathbb{R}$ 이지만, python의 "broadcasting"으로 인해 $\in \mathbb{R}^{1 \times m}$으로 자동으로 만들어진다.)
  • A = sigmoid(Z) (sigmoid는 예시로 작성한 것이다. 정확한 함수는 뒤에 나온다.)
    

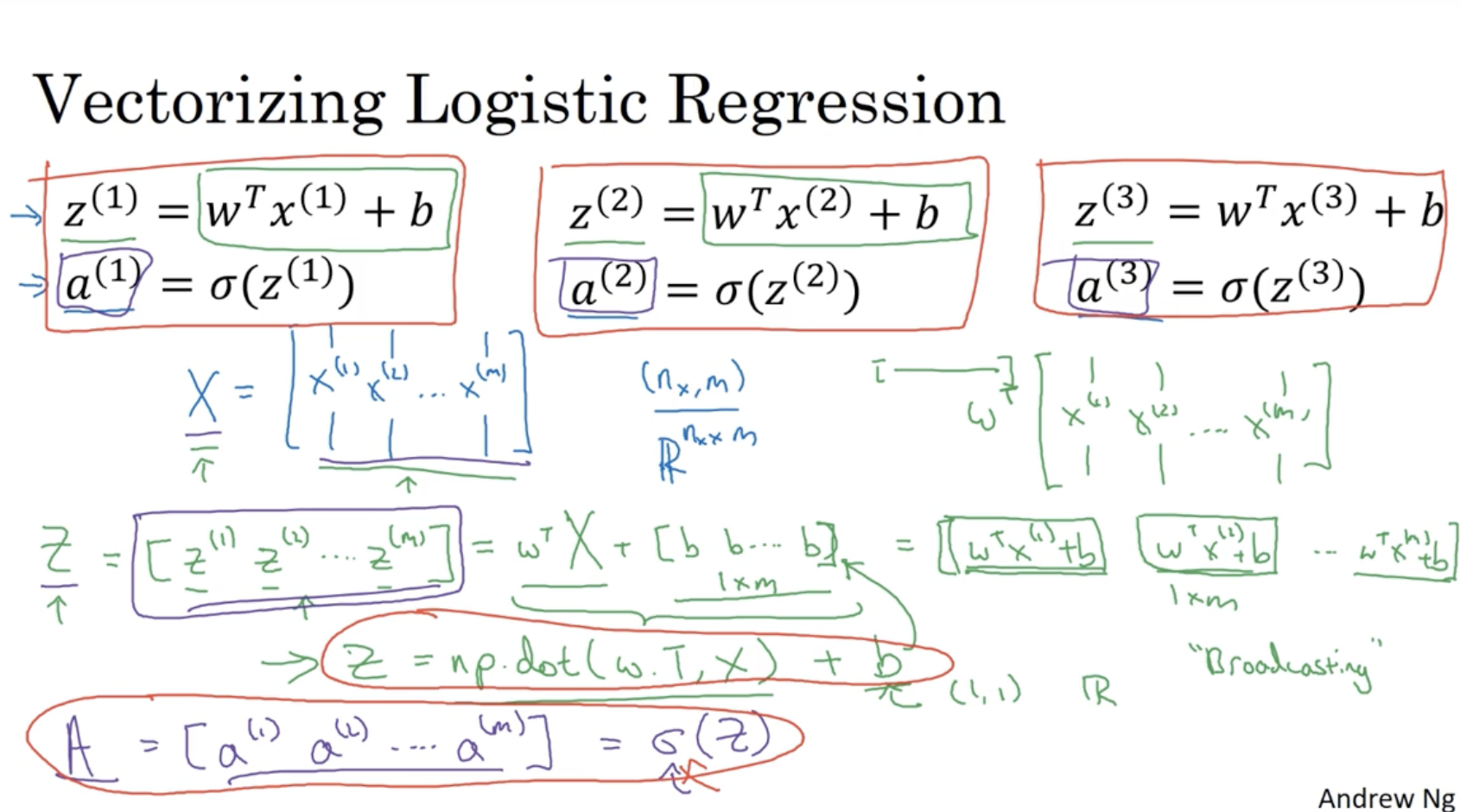
그럼 이제 나머지 값들도 vectorization을 적용해보자.

• $dz=\begin{bmatrix}dz^{(1)}, dz^{(2)}, ... , dz^{(m)}\end{bmatrix} \in \mathbb{R}^{1 \times m}$
  • $dz^{(i)}=a^{(i)}-y^{(i)}$
  • 따라서 Python에서 이를 구현하면, $dz=A-Y$로 구현이 가능하다.
• $dw=\frac{1}{m}\sum_{i=1}^{m}x^{(i)}dz^{(i)}$
  • $x^{(i)}=\begin{bmatrix}x^{(i)}_1 \\ x^{(i)}_2 \\ ... \\ x^{(i)}_n\end{bmatrix}$
  • 따라서 이를 vectorization 하면 다음과 같다. $dw=\frac{1}{m}X\cdot dz^T$
  • $dw \in \mathbb{R}^{n \times 1}$
• $db=\frac{1}{m}\sum_{i=1}^mdz^{(i)}$
  • python에서는 다음과 같이 구현 가능. db = 1/m * np.sum(dz)
    

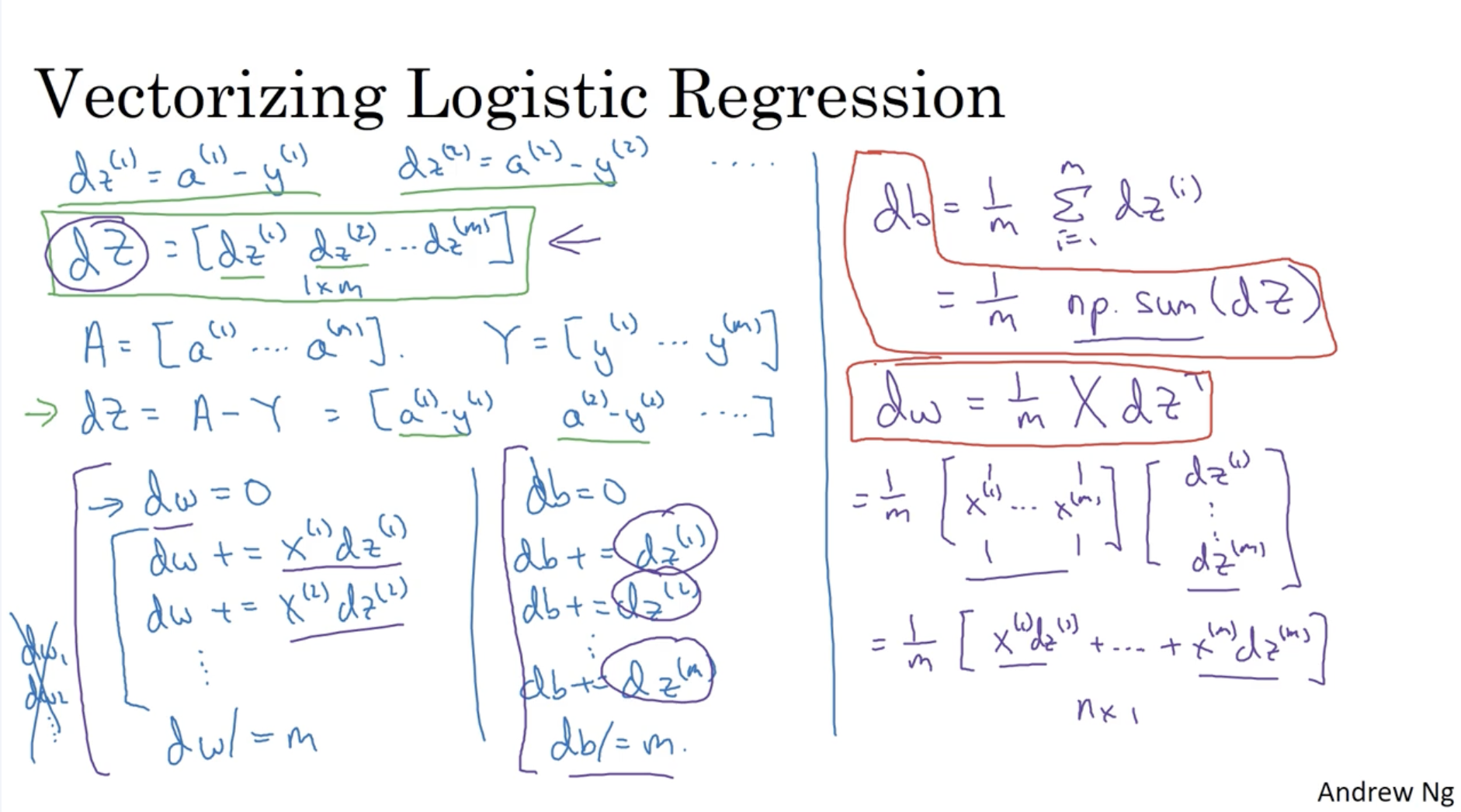
따라서 logistic regression을 Python에서 구현하면 우측과 같다.

• $Z=w^TX+b$
  • Z = np.dot(w.T, X) + b
  • $w \in \mathbb{R}^{n \times 1}$
  • $X \in \mathbb{R}^{n \times m}$
  • $b \in \mathbb{R}$
  • $Z \in \mathbb{R}^{1 \times m}$
• $A=\sigma(Z)$
  • A = sigma(Z)
  • $A \in \mathbb{R}^{1 \times m}$
• $dz=A-Y$
  • dz = A - Y
  • $Y \in \mathbb{R}^{1 \times m}$
  • $dz \in \mathbb{R}^{1 \times m}$
• $dw=\frac{1}{m}Xdz^T$
  • dw = 1/m * np.dot(X, dz.T)
  • $dw \in \mathbb{R}^{n \times 1}$
• $db=\frac{1}{m}\sum_{i=1}^{m}dz^{(i)}$
  • db = 1/m * np.sum(dz)
• gradient descent
  • $w := w- \alpha\times dw$
  • $b := b- \alpha\times db$