[딥러닝] Neural Networks and Deep Learning Week 3

출처 : https://www.coursera.org/specializations/deep-learning

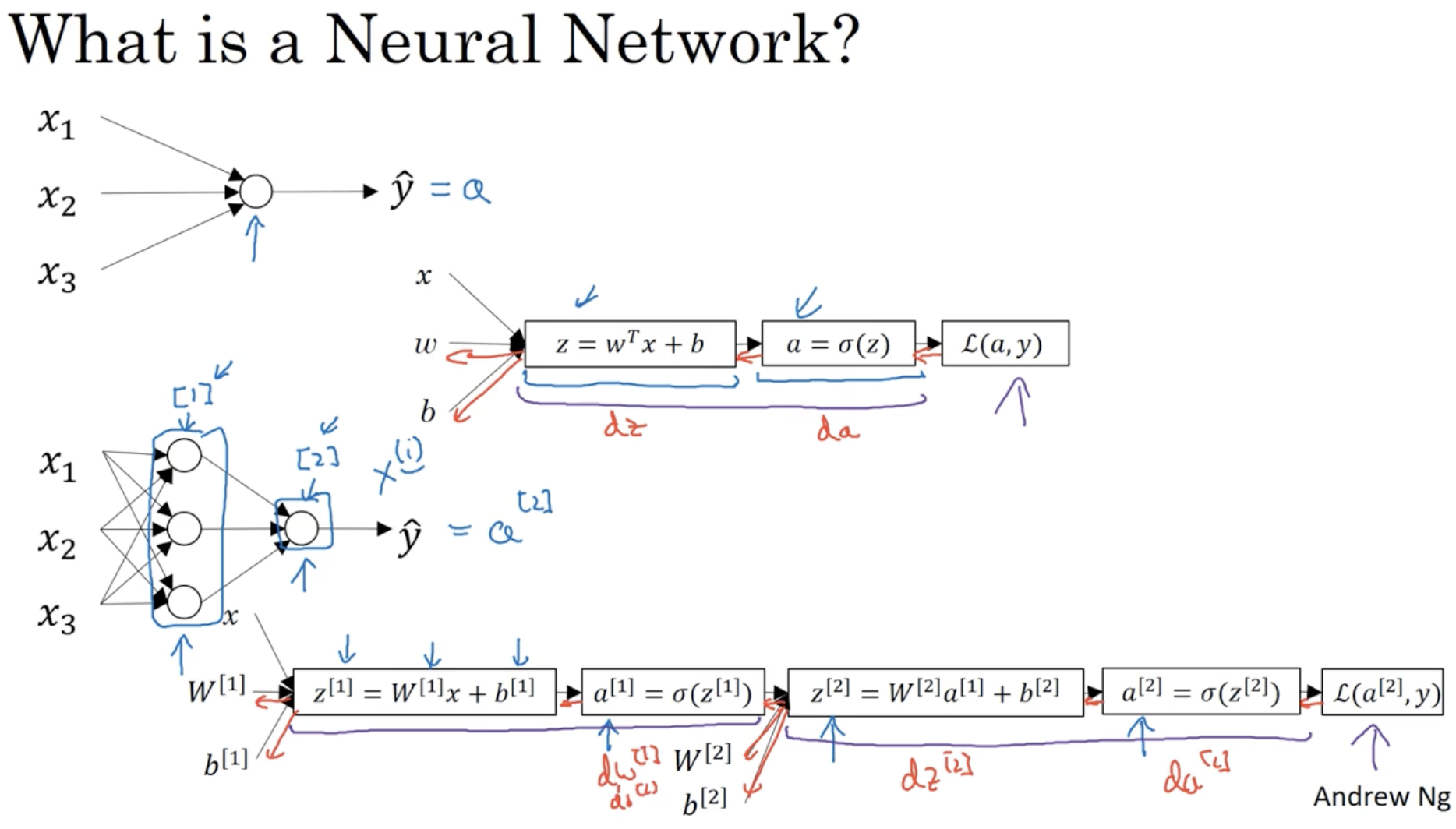
neural network의 개요는 다음과 같다.

• 이전에 봤던 Logistic regression을 여러 layer로 합친 것이라고 생각하면 편하다.
• 3개의 unit를 갖는 unit vector $a^{[1]}$를 만든다.
  • $z^{[1]}=W^{[1]}x+b^{[1]}$
  • $a^{[1]}=\sigma(z^{[1]})$
• unit 벡터 $a^{[1]}$을 가지고 다음 unit vector $a^{[2]}$를 구한다.
  • $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
  • $a^{[2]}=\sigma(z^{[2]})$
• 최종 값 $a^{[2]}=(\hat y)$를 가지고 Loss function $L(a^{[2]},y)$를 구한다.
• 그리고 위 과정은 forward propagation에 해당하며, back propagation을 적용하여 미분값을 구한 후 gradient descent alg.을 적용한다.
  • $da^{[2]}=\frac{\partial L(a^{[2]}, y)}{\partial a^{[2]}}$
  • $dz^{[2]}=\frac{\partial L(a^{[2]}, y)}{\partial z^{[2]}} = da^{[2]}\times \frac{\partial a^{[2]}}{\partial z^{[2]}}$
  • $dw^{[2]}=dz^{[2]}\times \frac{\partial z^{[2]}}{\partial w^{[2]}}$
  • $db^{[2]}=dz^{[2]}\times \frac{\partial z^{[2]}}{\partial b^{[2]}}$
  • ...
    

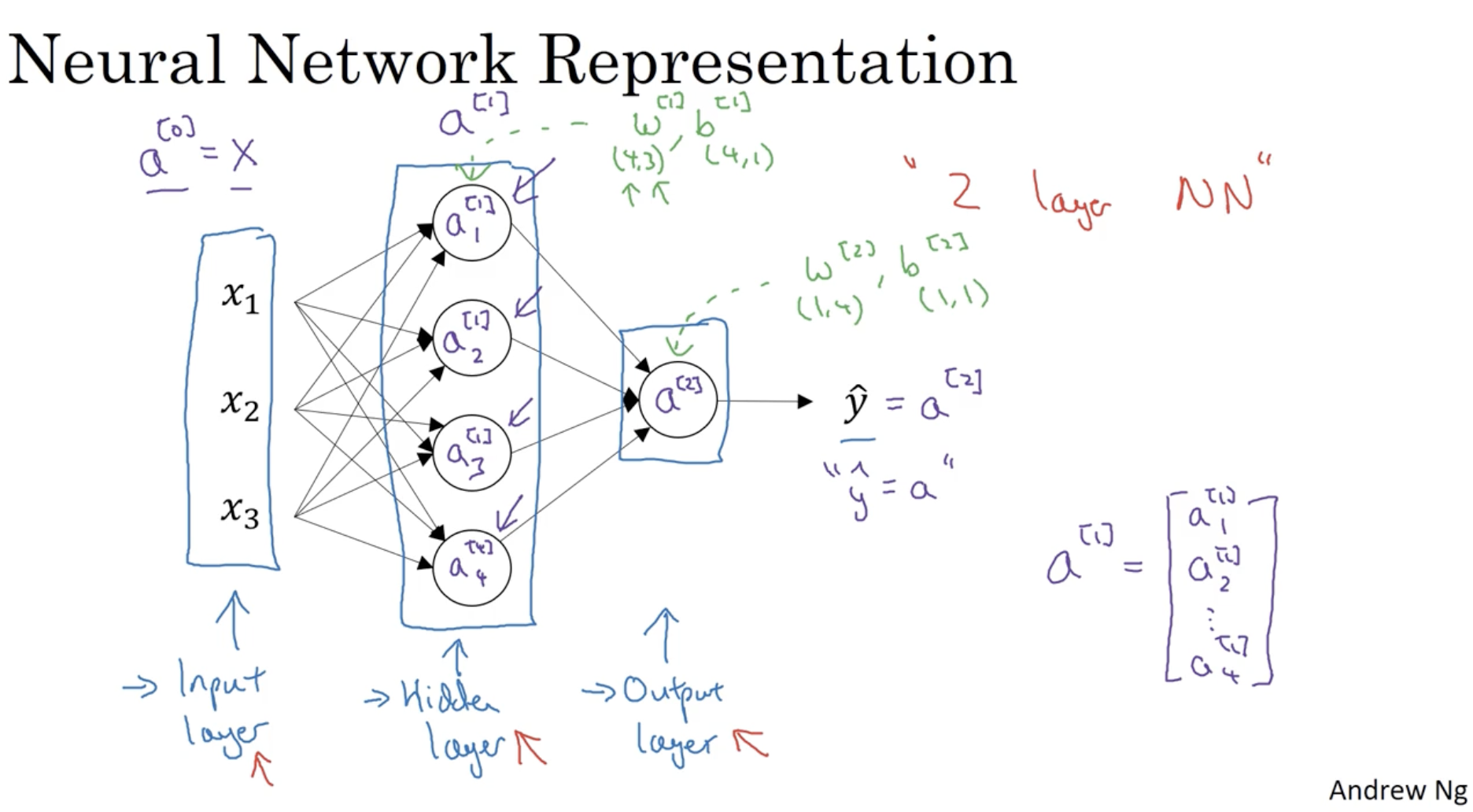
hidden layer가 1차원인 Neural Network의 구조는 아래와 같다.

• 먼저 입력 데이터 $x=\begin{bmatrix}x_1 \\ x_2 \\ x_3\end{bmatrix}$를 $a^{[0]}=x$로 본다.
• 다음으로 $W^{[1]}, b^{[1]}$를 가지고 다음 레이어의 유닛 벡터 $a^{[1]}$을 구한다.
  • 다음 레이어의 유닛 수에 따라 $W^{[1]}, b^{[1]}$의 차원이 결정된다.
• 마지막으로 $W^{[2]}, b^{[2]}$를 가지고 마지막 레이어의 유닛 벡터 $a^{[2]}$를 구한다.
  • 마찬가지로 마지막 레이어의 유닛 수에 따라 $W^{[2]}, b^{[2]}$의 차원이 결정된다.
• 따라서 최종 예측값 $\hat y=a^{[2]}(=a)$를 구한다.
  

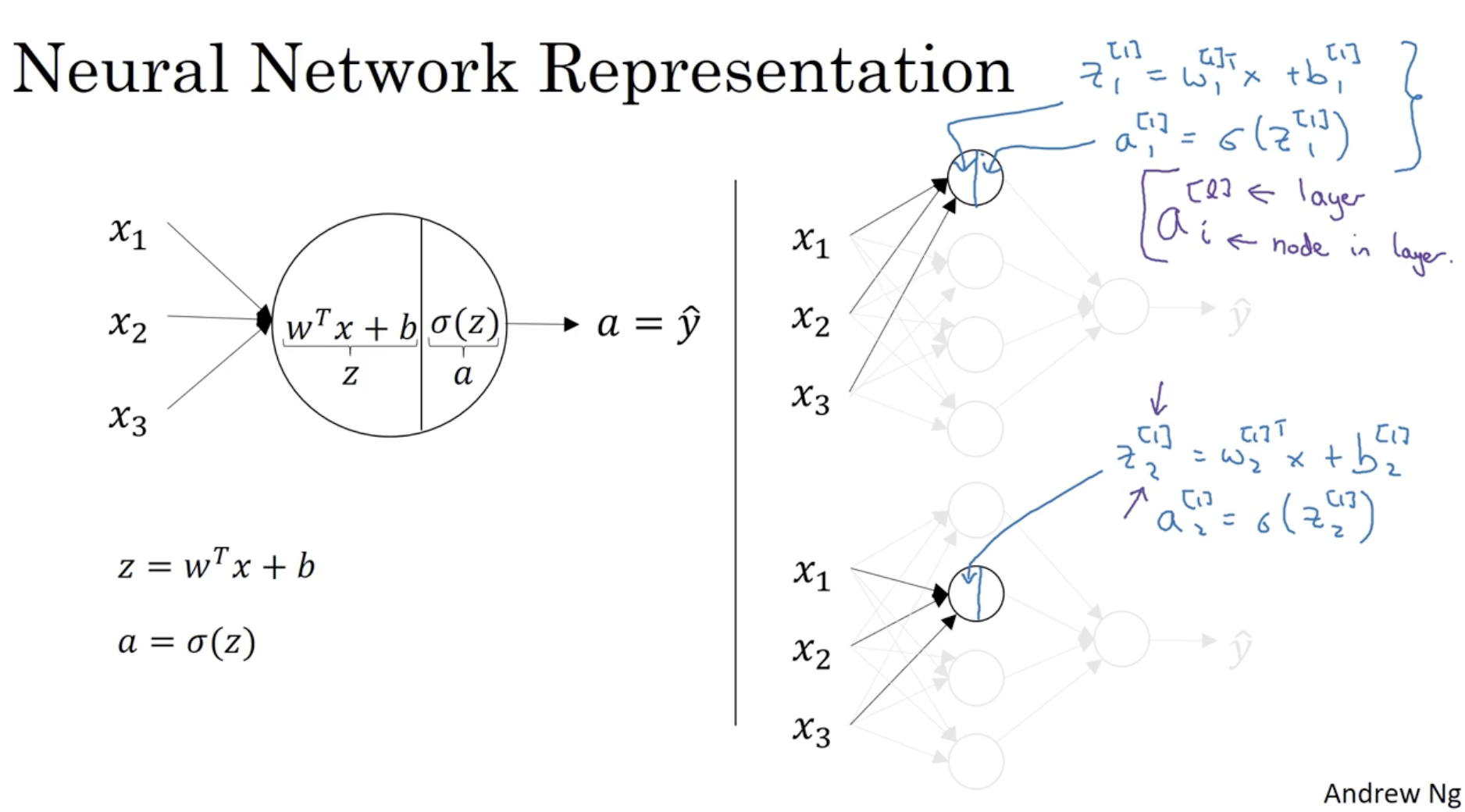
구체적으로 하나의 입력 데이터 $x$에 대해서 neural network가 어떤 식으로 동작하는 지 알아보자.

• $z=w^Tx+b$
  • $w \in \mathbb{R}^{n \times 1}, x \in \mathbb{R}^{n \times 1}, b \in \mathbb{R}$
  • $z \in \mathbb{R}$
• $a=\sigma(z)$
  • $a \in \mathbb{R}$
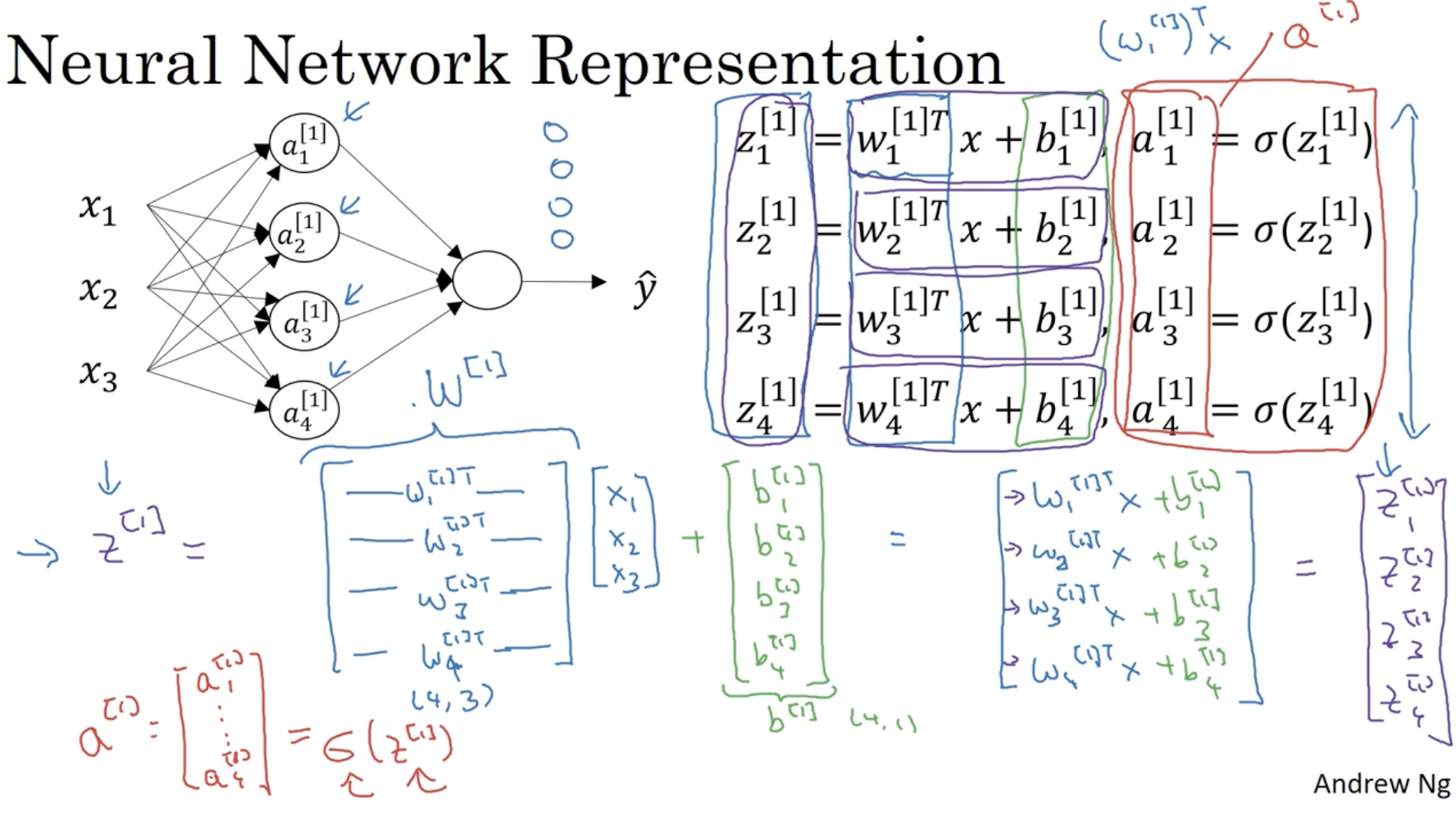
• 위 수식을 그대로 적용하여 각각의 hidden layer unit $a^{[1]}_1,a^{[1]}_2,a^{[1]}_3,a^{[1]}_4$를 구할 수가 있다.
  • $a^{[l]}_i$ : $l$은 layer를 의미, $i$는 node를 의미.
    

따라서 구체적으로 다 계산을 해보면 아래와 같은 결과를 얻을 수가 있다. (1번 레이어를 기준으로 본다.)
($z^{[1]}_1,a^{[1]}_1,...,z^{[1]}_4,a^{[1]}_4$)
그리고 이를 일일이 계산하는 것이 아니라 vectorization을 적용하면 아래와 같다.

• $W^{[1]}=\begin{bmatrix}-(w^{[1]}_1)^T- \\ -(w^{[1]}_2)^T- \\ -(w^{[1]}_3)^T- \\ -(w^{[1]}_4)^T- \\ \end{bmatrix} \in \mathbb{R}^{4 \times 3}$, $x=\begin{bmatrix}x_1 \\ x_2 \\ x_3\end{bmatrix} \in \mathbb{R}^{3 \times 1}$, $b^{[1]}=\begin{bmatrix}b_1^{[1]} \\ b_2^{[1]} \\ b_3^{[1]} \\ b_4^{[1]}\end{bmatrix} \in \mathbb{R}^{4 \times 1}$
• $z^{[1]}=\begin{bmatrix}z_1^{[1]} \\ z_2^{[1]} \\ z_3^{[1]} \\ z_4^{[1]}\end{bmatrix} \in \mathbb{R}^{4 \times 1}$, $a^{[1]}=\begin{bmatrix}a_1^{[1]} \\ a_2^{[1]} \\ a_3^{[1]} \\ a_4^{[1]}\end{bmatrix} \in \mathbb{R}^{4 \times 1}$
• 따라서 식을 정리하면 다음과 같다.
• $z^{[1]}=W^{[1]}x+b^{[1]}$
• $a^{[1]}=\sigma(z^{[1]})$
  

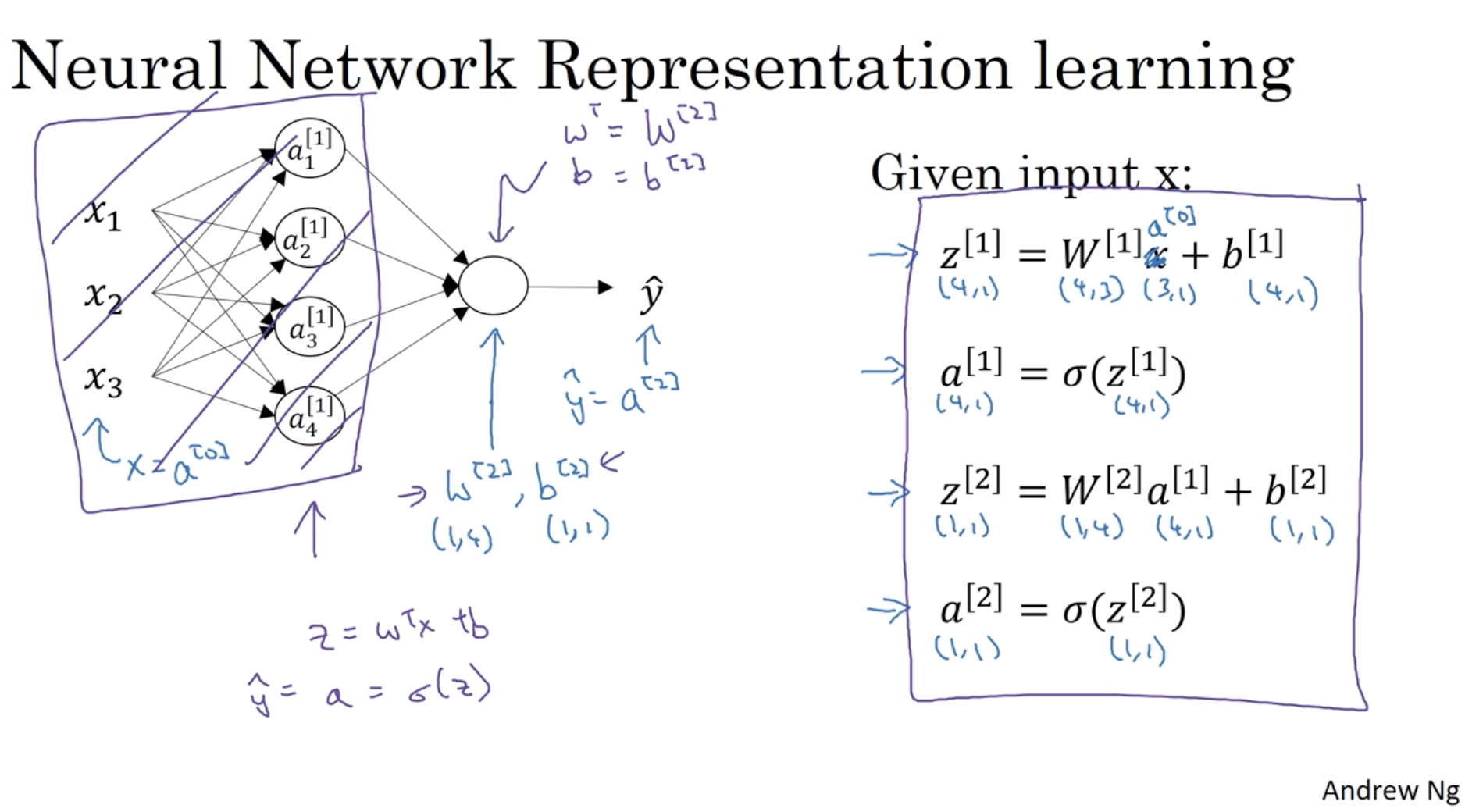
모든 레이어에 대해 깔끔하게 정리하면 아래와 같다.

• 하나의 데이터 $x$가 주어졌을 때.
• 1번 레이어 (hidden layer) :
  • $z^{[1]}=W^{[1]}x+b^{[1]}$
  • $a^{[1]}=\sigma(z^{[1]})$
• 2번 레이어 (output layer) :
  • $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
  • $a^{[2]}=\sigma(z^{[2]})$
    

그렇다면 1개의 데이터가 아닌 여러 개의 데이터에 대해서 적용한다면 어떨까? 아래를 보자.

• 보다시피 for 문을 통해서 $m$개의 데이터 $x^{(1)},x^{(2)},...,x^{(m)}$에 대해서 각각의 $z^{[l](1)}, a^{[l](1)},...,z^{[l](m)}, a^{[l](m)}$을 구하고 있음을 알 수 있다.
• 이처럼 for-loop를 통해서 구현할 경우, 연산 속도가 매우 느려질 것이다. 따라서 여기에 Vectorization을 적용한다.
  

Vectorization 방법은 간단하다.

• $X=\begin{bmatrix} | & | & ... & | \\ x^{(1)} & x^{(2)} & ... & x^{(m)} \\ | & | & ... & | \\ \end{bmatrix} \in \mathbb{R}^{n_x \times m}$ ($X=A^{[0]}$으로 본다.)
• $Z^{[l]}=\begin{bmatrix} | & | & ... & | \\ z^{[l](1)} & z^{[l](2)} & ... & z^{[l](m)} \\ | & | & ... & | \\ \end{bmatrix} \in \mathbb{R}^{ \text{\# of hidden units} \times m}$
• $A^{[l]}=\begin{bmatrix} | & | & ... & | \\ a^{[l](1)} & a^{[l](2)} & ... & a^{[l](m)} \\ | & | & ... & | \\ \end{bmatrix} \in \mathbb{R}^{ \text{\# of hidden units} \times m}$
• 따라서 식을 정리하면 다음과 같다.
  • $Z^{[1]}=W^{[1]}X+b^{[1]}$
  • $A^{[1]}=\sigma(Z^{[1]})$
  • $Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}$
  • $A^{[2]}=\sigma(Z^{[2]})$
    

사실 Neural Networks에서 Activation function는 sigmoid뿐만 아니라 다양한 함수가 존재한다.

• $sigmoid=\sigma(z)=\frac{1}{1+e^{-z}} \rightarrow (0, 1)$
• $tanh(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} \rightarrow (-1,1)$
• $ReLU=max(0,z) \rightarrow [0,\infty]$
• $Leaky \ ReLU=max(0.01z,z) \rightarrow [-\infty, \infty]$
• 보통 ReLU, tanh, sigmoid 순으로 성능이 좋다. (Leaky ReLU은 추천하지 않는다.)
• 따라서 hidden layer unit의 activation function으로 ReLU를 보통 많이 사용한다.
• 하지만, 최종 output layer unit의 activation function은 (예측값인) 0 ~ 1 사이의 값을 가져야 하기 때문에 무조건 sigmoid를 사용하여야 한다.
• 레이어마다 다른 activation function을 적용할 수 있다.
  $l$ 번째 레이어의 activation function 표기 : $g^{[l]}(z^{[l]})$
  

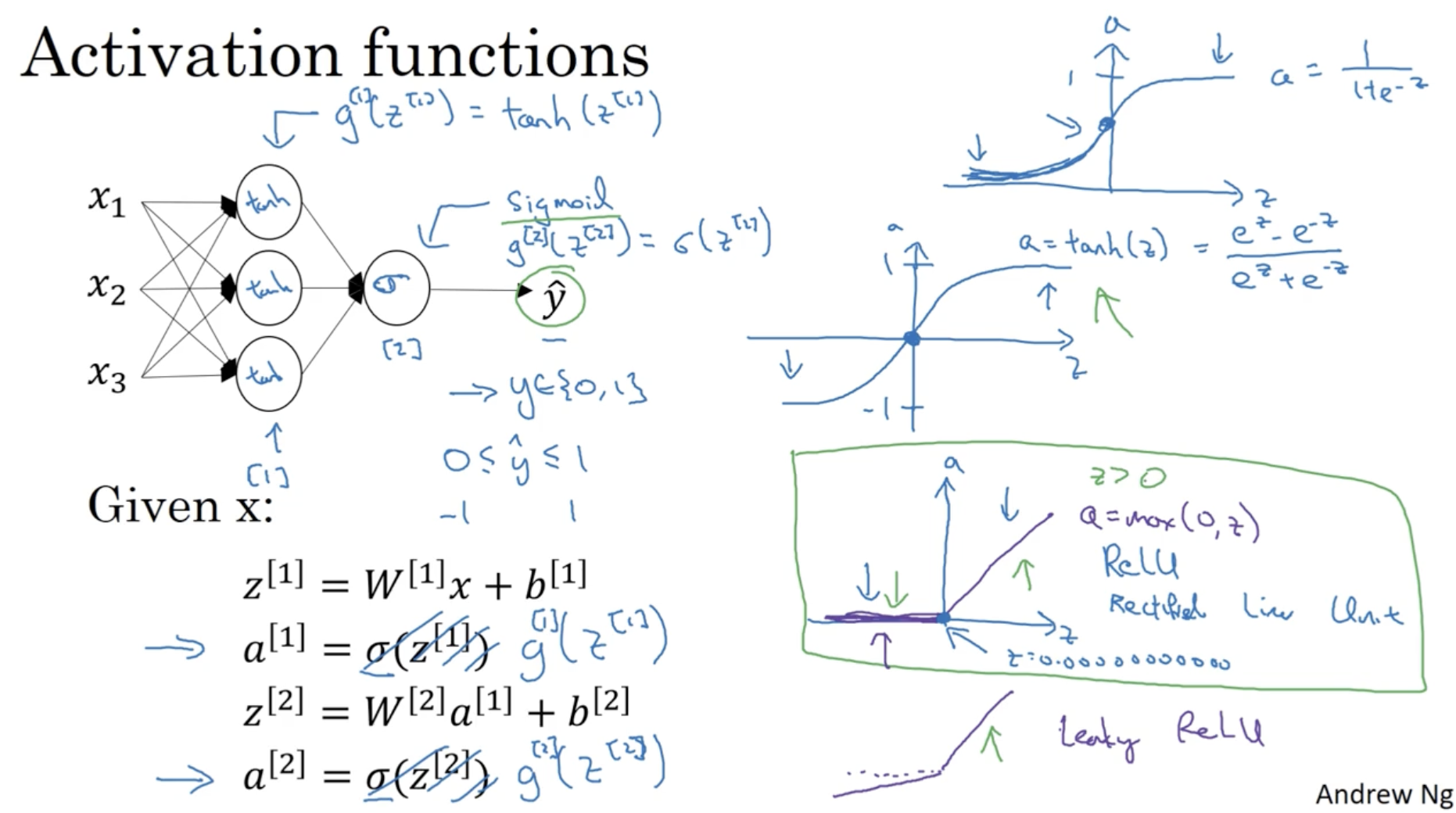
각 activation function을 그래프로 그려보면 아래와 같다.

• ReLU의 경우 0 이하의 값은 기울기 0이며, $z > 0$일 경우에는 기울기가 1이다. 따라서 gradient descent alg. 측면에서 속도가 매우 빠르다는 장점이 있다. 따라서 해당 activation function을 가장 많이 사용한다.
• 그렇다면 만약 $g(z)=z$와 같이 항상 기울기가 1이 되는 linear한 activation function을 적용하면 gradient descent 속도가 더 빨라지지 않을까? 다음 내용을 보자.
  

Neural Networks에서 linear function을 activation function으로 선택하지 않는 이유는
"linear activation function을 적용하면 Neural Networks의 이점이 없기 때문이다."

• 아래에서 우측 식을 보면, linear activation function ($a=g(z)=z$)을 적용할 경우, 모든 $a^{[l]}$에 대하여 결국에는 $a^{[l]}=w'x+b$와 같은 꼴로 나오게 된다. 이렇게 될 경우, 히든 레이어 간의 변별력은 없어진다.
• 아래 neural networks 구조처럼 히든 레이어 유닛에 linear activation function을 적용하고, 마지막에 sigmoid를 적용할 경우, 이는 그저 logistic regression에 불과하다. 즉, 뉴럴넷의 장점을 활용하지 못한다.
• 따라서 hidden layer unit에는 non-linear activation function이 적용되어야 한다.
  

물론 아래 뉴럴넷의 구조처럼 마지막에 linear activation function (혹은 ReLU)를 적용하는 경우도 있다. 이 경우는 집 가격 예측과 같이 선형성을 띄는 경우에 해당한다. (집 가격은 무조건 0 이상이기 때문에 ReLU도 적용 가능.)

이제 각 activation function의 미분 식을 알아보자.

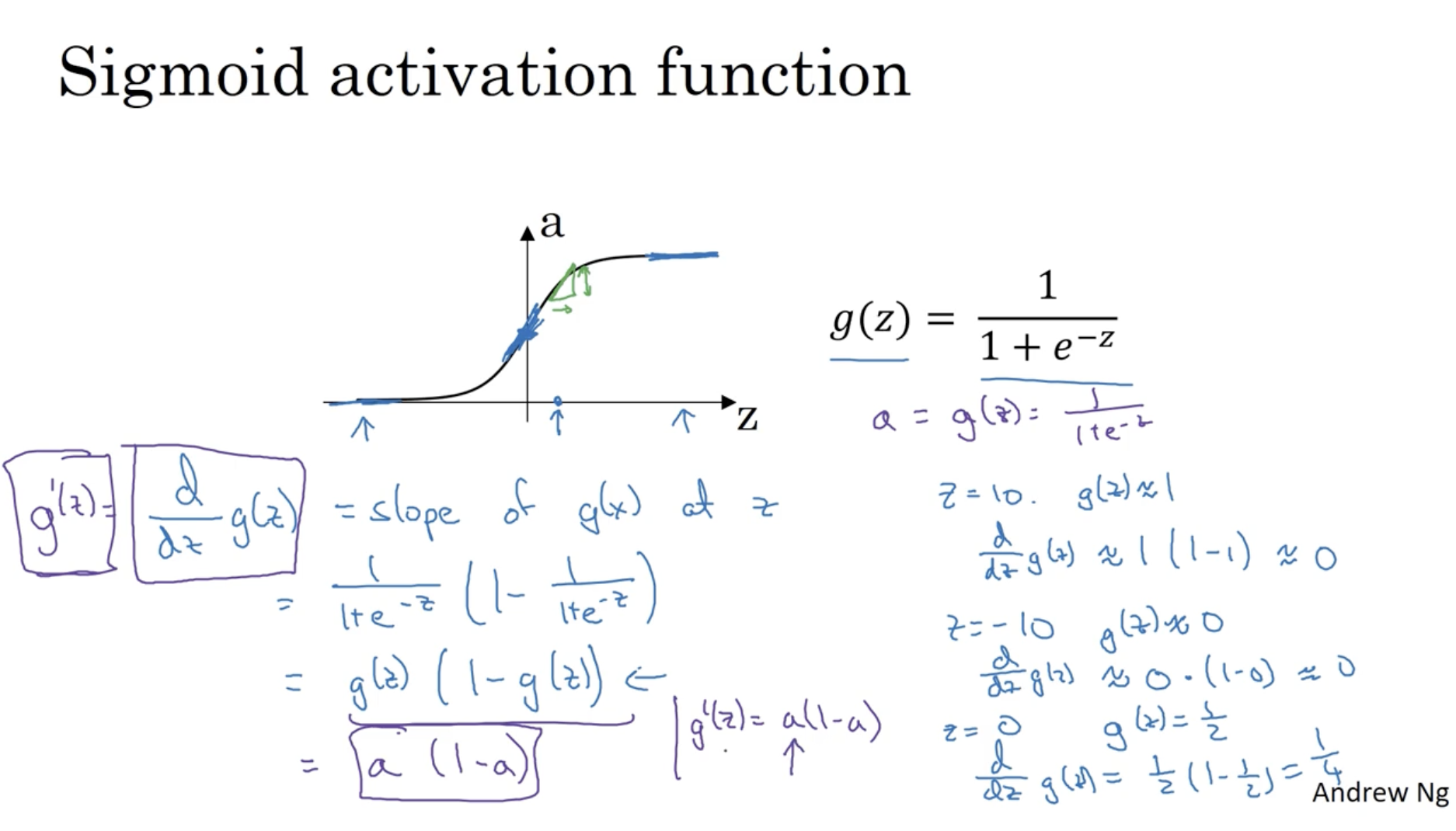
• 아래는 sigmoid 함수에 대한 미분값을 구하는 과정이다.
• sigmoid의 미분 식은 다음과 같다.
  $g'(z)=\frac{d}{dz}g(z)=g(z)(1-g(z))=a(1-a)$
• $g'(0)=\frac{1}{2}\times(1-\frac{1}{2})=\frac{1}{4}$
  

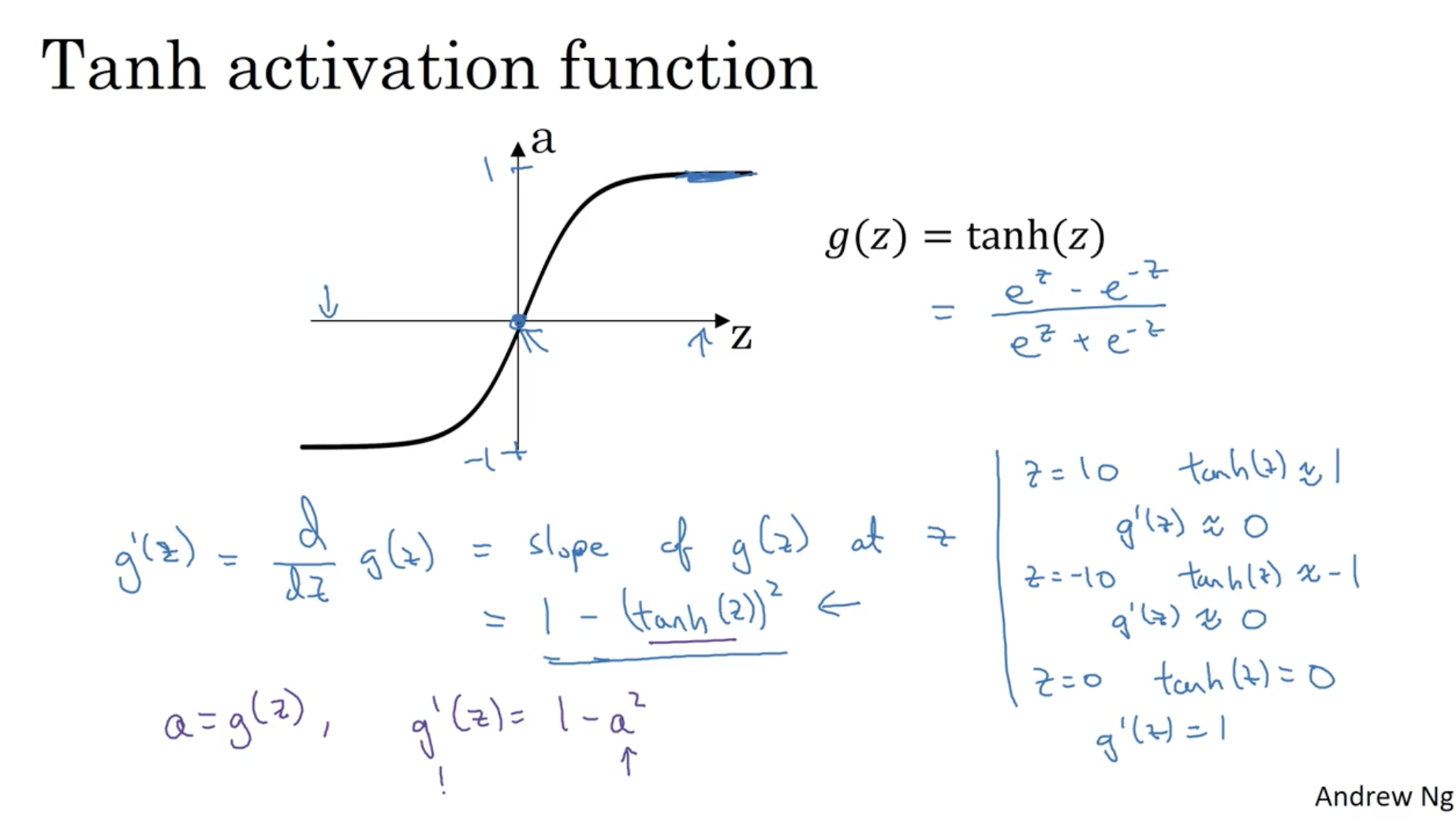
다음은 tanh의 미분값을 구하는 식이다.

• tanh의 미분 식은 다음과 같다.
  $g'(z)=\frac{d}{dz}g(z)=1-(g(z))^2=1-a^2$
• $g'(0)=1 - (0)^2=1$
  

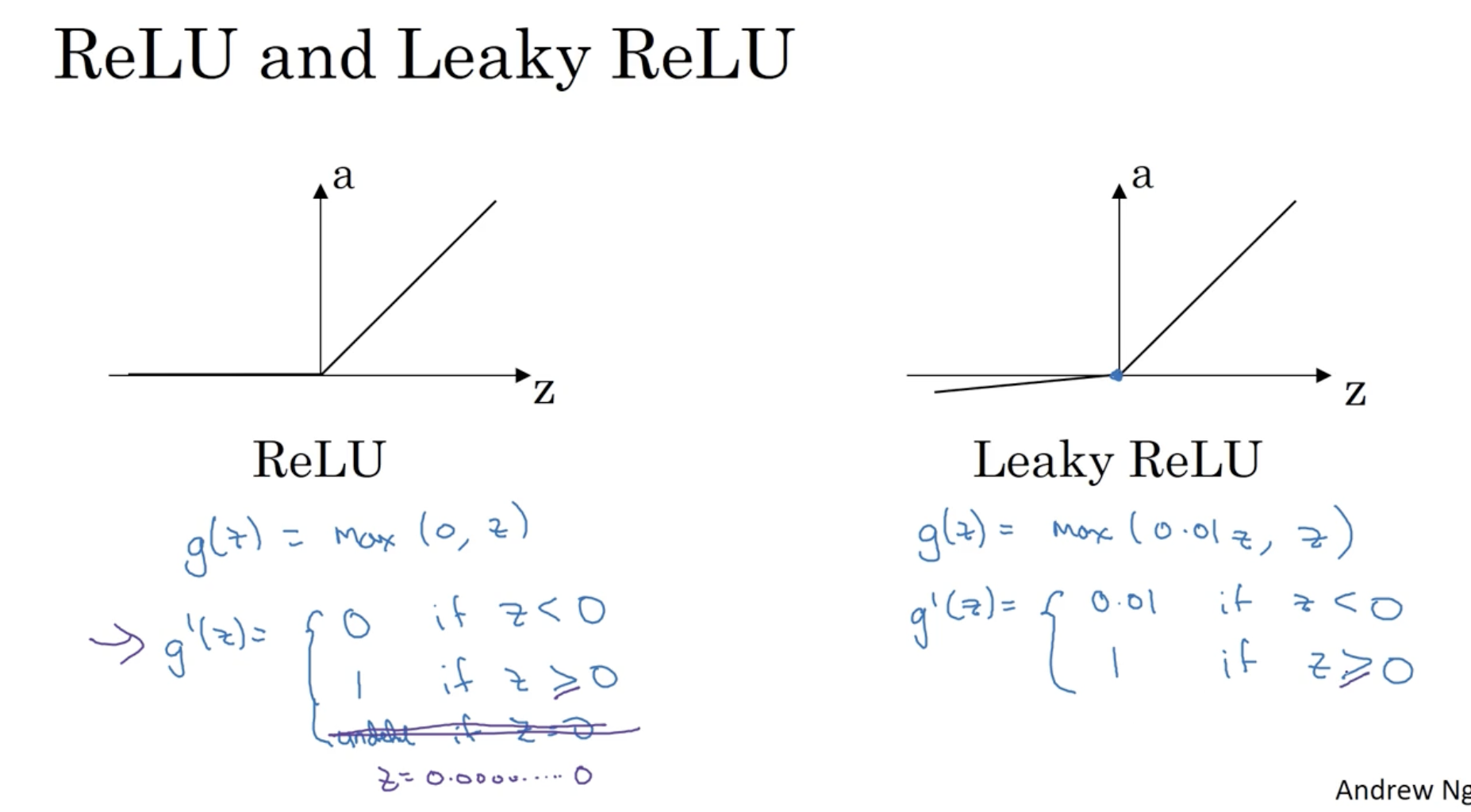
다음은 ReLU와 Leaky ReLU의 미분 공식이다.

• ReLU : $g'(z) = \begin{cases} 0, & \text{if } z < 0 \\ 1, & \text{if } z \ge 0 \end{cases}$ (컴퓨터에서는 정확히 0을 표현할 수 없기에 0일 때는 따로 고려하지 않아도 된다.)
• Leaky ReLU : $g'(z) = \begin{cases} 0.01, & \text{if } z < 0 \\ 1, & \text{if } z \ge 0 \end{cases}$
  

이제 Neural Network에 gradient descent를 적용하는 방법을 알아보자.

• 입력 데이터 $x$의 features 수는 $n_x=n^{[0]}$이며, hidden layer의 유닛 수는 $n^{[1]}$, output layer의 유닛 수는 $n^{[2]}=1$이다.
• 파라미터 정보는 다음과 같다.
  • $W^{[1]} \in \mathbb{R}^{n^{[1]}\times n^{[0]}}$
  • $b^{[1]} \in \mathbb{R}^{n^{[1]}\times 1}$
  • $W^{[2]} \in \mathbb{R}^{n^{[2]}\times n^{[1]}}$
  • $b^{[2]} \in \mathbb{R}^{n^{[2]}\times 1}$
• Cost function은 다음과 같다. $J(W^{[1]}, b^{[1]},W^{[2]}, b^{[2]})=\frac{1}{m}\sum_{i=1}^{m}L(\hat y^{(i)}, y^{(i)})$
• 따라서 gradient descent를 적용하면 다음과 같다.
  • $\text{predict}:(\hat y^{(1)},\hat y^{(2)},...,\hat y^{(m)})$
  • $dw^{[1]}=\frac{\partial J}{\partial W^{[1]}}, db^{[1]}=\frac{\partial J}{\partial b^{[1]}}, dw^{[2]}=\frac{\partial J}{\partial W^{[2]}}, db^{[2]}=\frac{\partial J}{\partial b^{[2]}}$
  • $W^{[1]}:=W^{[1]}-\alpha \times dw^{[1]}$
  • $b^{[1]}:=b^{[1]}-\alpha \times bw^{[1]}$
  • $W^{[2]}:=W^{[2]}-\alpha \times dw^{[2]}$
  • $b^{[2]}:=b^{[2]}-\alpha \times bw^{[2]}$
    

좀더 구체적으로 적으면 다음과 같다.

• 먼저 Forward Propagation을 통해 $Z^{[1]},A^{[1]}, Z^{[2]},A^{[2]}$의 값을 구한다.
• 다음으로 Back Propagation을 통해 $dz^{[2]},dw^{[2]},db^{[2]},dz^{[1]},dw^{[1]},db^{[1]}$ 값을 구한다.
  • $dz^{[2]}=A^{[2]}-Y$
  • $dw^{[2]}=\frac{1}{m}dz^{[2]}{A^{[1]}}^T$
  • $db^{[2]}=\frac{1}{m}np.sum(dz^{[2]}, \ axis=1, \ keepdims=True)$
  • $dz^{[1]}=({W^{[2]}}^Tdz^{[2]}) .* (g'^{[1]}(Z^{[1]}))$ (이 부분은 이해가 잘 안된다. 왜 이렇게 나오는 걸까.. 아래 chat gpt를 통해 알아냈다. 쉽게 생각해서 $dz^{[1]}=\frac{\partial J}{\partial A^{[1]}}\times\frac{\partial A^{[1]}}{\partial Z^{[1]}}$이다. 그러나 강의에서는 $\frac{\partial J}{\partial A^{[1]}}$를 따로 표기하지 않아서 헷갈렸던 것 같다.)
  • $db^{[1]}=\frac{1}{m}np.sum(dz^{[1]}, \ axis=1, \ keepdims=True)$
    
    $dz^{[1]}$의 유도 과정
    

Neural Networks의 미분 과정을 logistic regression과 비교했을 때 유사하다는 것을 확인할 수가 있다.

• $dw^{[2]}=dz^{[2]}{a^{[1]}}^T$ vs. $dw=dz\cdot x$
  • $z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$ 식에서 logistic regression의 $x$에 해당하는 $a^{[1]}$을 볼 수가 있다.
• 또한 Neural Networks에서는 foo$(W^{[l]},Z^{[l]},...)$와 dfoo$(dw^{[l]}, dz^{[l]}, ...)$의 차원이 같다는 것을 알 수가 있다.
  

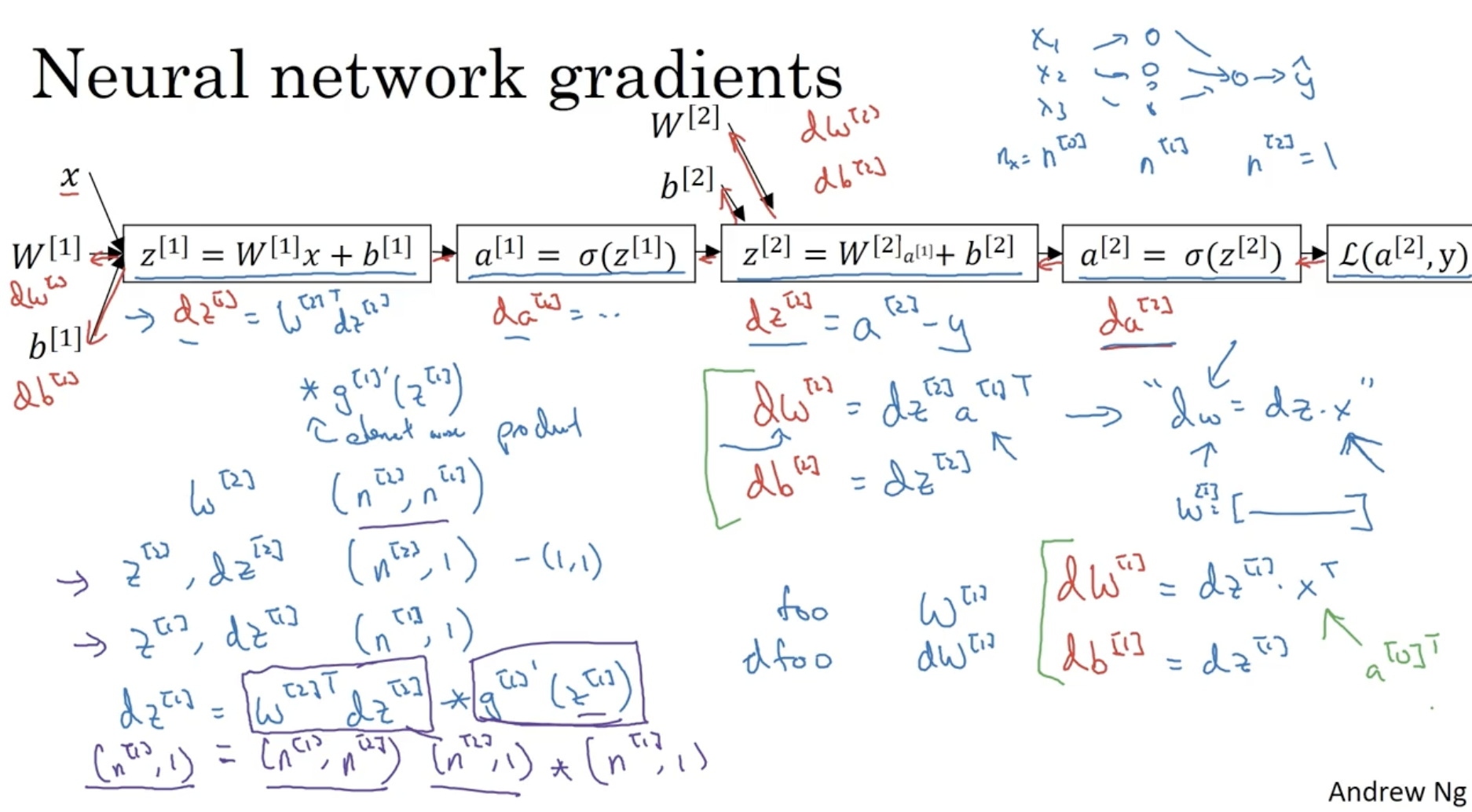
그리고 하나의 데이터에 대해서 적용하는 것 대신, Vectorization을 적용할 수도 있다.

• 좌측은 하나의 데이터에 대한 예시이며, 우측은 vectorization을 적용한 예시이다.
  

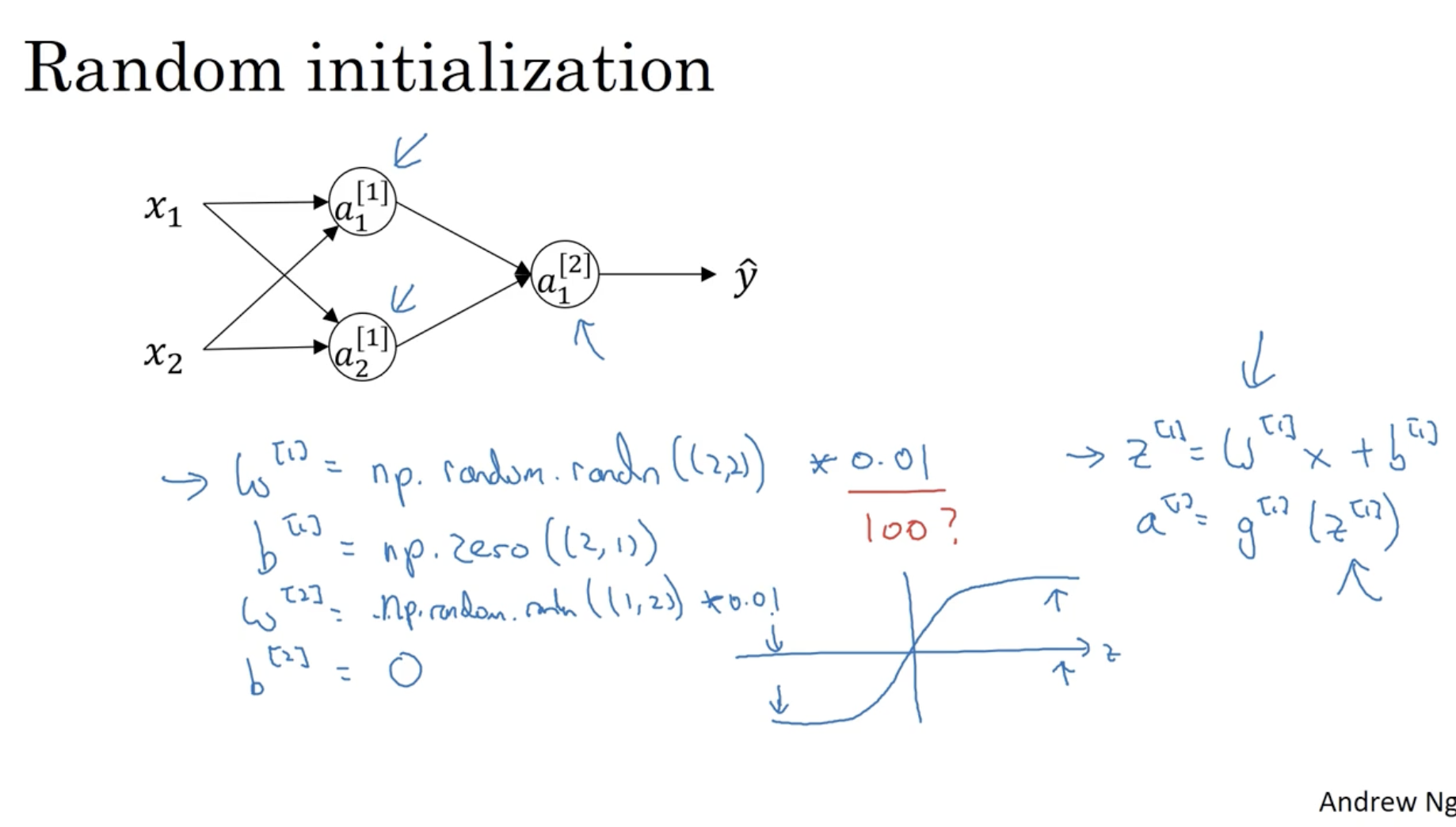
그렇다면 만약 초기 파라미터 $W, b$를 0으로 초기화한다면 어떻게 될까?

• 먼저 forward propagation을 적용했을 때, 같은 레이어의 유닛들의 값은 모두 동일하게 나올 것이다.
• 그리고 back propagation을 통해 gradient descent alg.을 적용하여 $W,b$값을 갱신해도 $W,b$의 원소값들은 모두 동일하게 나오고, 이로 인해 역시 다시 forward propagation을 진행해도 모든 유닛들의 값이 동일하게 나오게 된다.
• 이처럼 유닛들 간의 차이가 없어지게 되므로 이는 Nueral Networks.을 사용하는 의미가 없어진다.
  

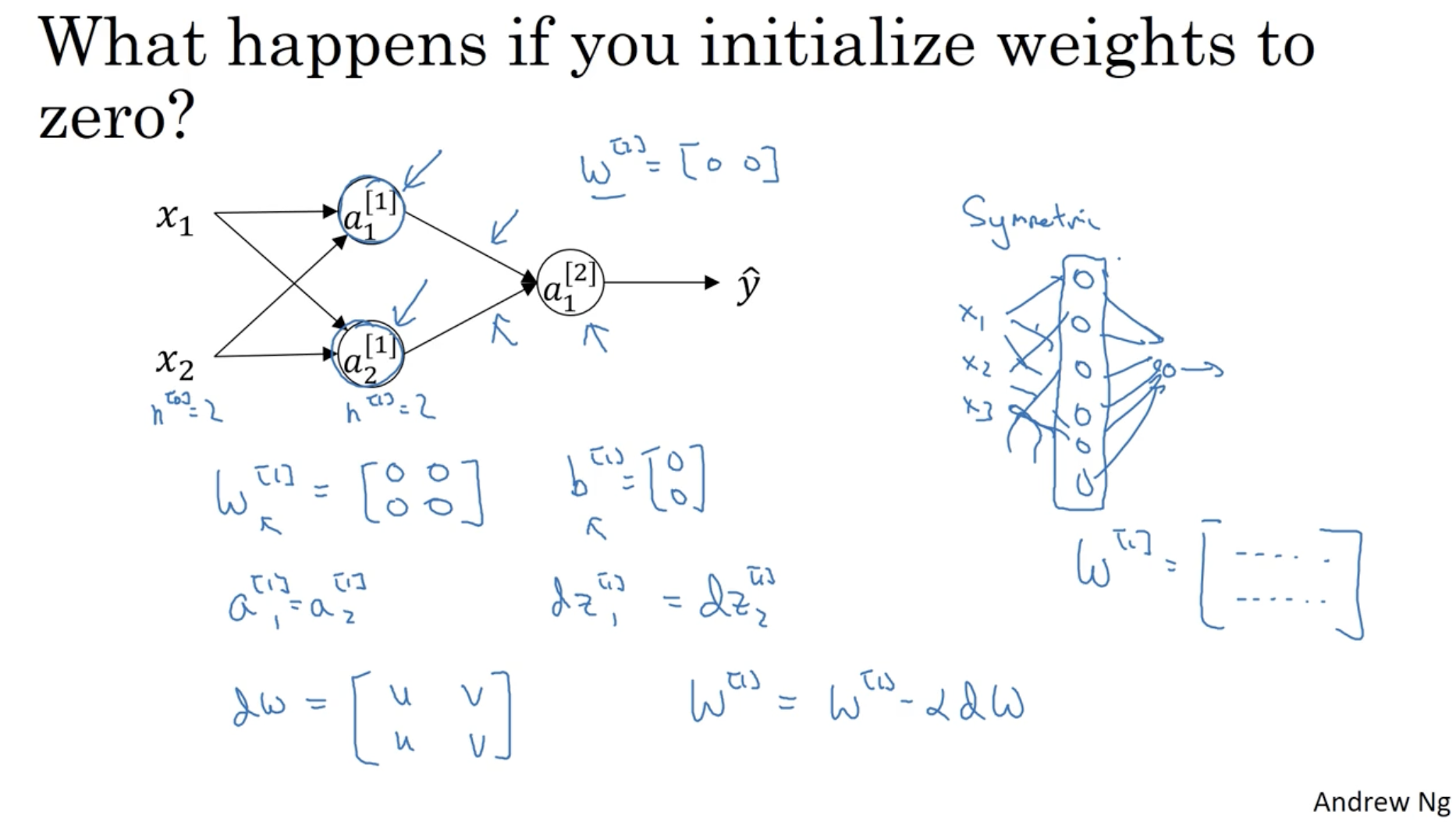
따라서 파라미터의 값을 랜덤하게 초기화하는 것이 좋다.

• $W^{[1]}=np.random.randn((2,2))*0.01$
  • 여기서 0.01을 곱해주는 이유는 초기 파라미터의 값이 매우 작게 나와야 gradient descent의 속도가 빠르기 때문이다.
  • 예를 들어, tanh activation function에 적용하는 $tanh(z=W^Tx+b)$ $z$의 값이 매우 크거나 작을 경우, 해당 값의 기울기는 0에 가까울 것이며, 이럴 경우 gradient descent 속도가 매우 느릴 것이다.
• $b^{[1]}=np.zeros((2,1))$
  • 하지만 weight parameter $W$와 달리 $b$는 0으로 초기화해도 괜찮다.