[프로그래머스][Python] 스티커 모으기(2)

[프로그래머스][Python] 스티커 모으기(2), level 3

문제

문제 설명

N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

제한 사항

sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

입출력 예

sticker	answer
[14, 6, 5, 11, 3, 9, 2, 10]	36
[1, 3, 2, 5, 4]	8

입출력 예 설명

입출력 예 #1

6, 11, 9, 10이 적힌 스티커를 떼어 냈을 때 36으로 최대가 됩니다.

입출력 예 #2

3, 5가 적힌 스티커를 떼어 냈을 때 8로 최대가 됩니다.

---

접근

조금 고민하다가 dp문제임을 알았다.
문제는 배열이 선형이 아닌 원형이라는 것
어떤 조건으로 원형을 반영해야하는지 고민하는데 시간이 오래 걸렸다..

이럴 때 시간을 많이 쓰는 이유는 연습이 부족해서도 있겠지만,
문제를 직관으로 풀려다가 꼬이는 경우가 대부분이다.
논리적으로 하나하나 풀어가는게 느려보여도 안정적인 시간 복잡도를 가지는 풀이이니,
조금 침착하게 하나씩 짚어가며 푸는 연습을 해야겠다.

풀이

dp 테이블은 sticker 길이의 배열 2개로 구성된 2차원 배열로 선언하였다.

dp[0]은 0번 스티커를 선택한 경우의 최대값을,
dp[1]은 1번 스티커를 선택한 경우의 최대값을 구하기 위한 배열이다.

왜 두 경우를 나누어야 하냐면,
1번 스티커를 선택하며 시작할 경우에는 상관없지만,
0번 스티커를 선택하며 시작할 경우에는 마지막 스티커를 사용하지 못하기 때문이다.

결국 이는 마지막 스티커를 사용할 수 있는 경우 와 그렇지 않은 경우 를 구분하기 위한 방법이다.

이제 dp 테이블을 입출력 예시로 나온 sticker를 이용해서 갱신해보자

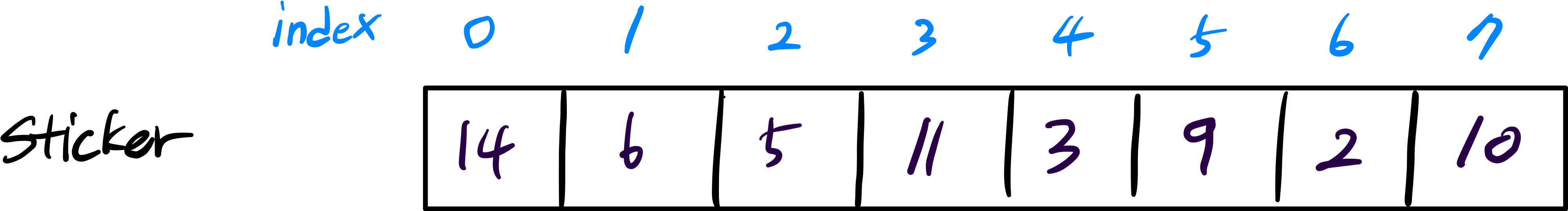
sticker[0]은 14,
sticker[1]은 6 이다.

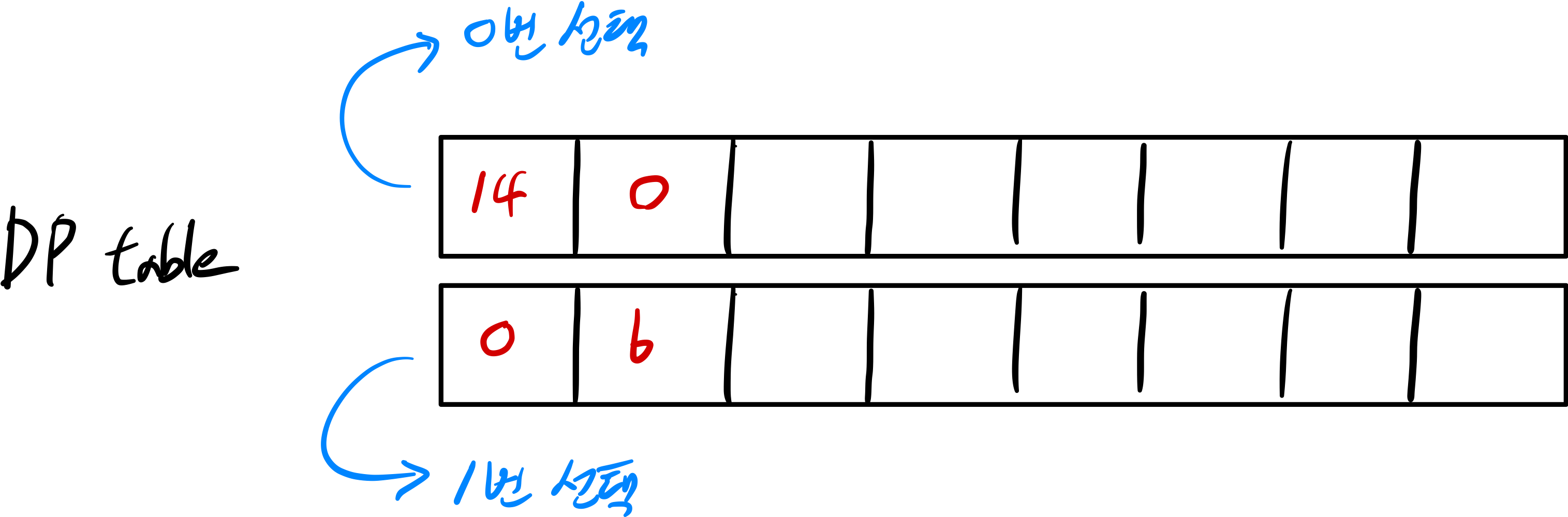
dp[0][1] 과 dp[1][0] 은 각각 선택되지 못했기 때문에 값이 없는것이 맞으나, 계산의 편의를 위해 0으로 초기화해주었다.

두 배열의 2번 인덱스는 각각
sticker[2] + dp[0][2-2]
sticker[2] + dp[1][2-2]로 갱신해주었다.
이 과정에서 3칸 뒤의 스티커를 사용할지 여부는 아직 계산에 반영하지 않는다.
3칸 뒤에 있는 스티커는 마지막 스티커이기 때문이며,
이는 배열을 순회하며 마지막에 계산해야할 요소이기 때문이다.

이후 부터 i번째 인덱스는 dp테이블의 max(i-2, i-3) 을 각 배열의 원소값에 더해주며 위와 같이 갱신한다.
마지막 요소만 남겨놓은 이유는,
dp 테이블을 2차원 배열로 선언한 이유인 '마지막 요소가 사용 가능한 경우와 그렇지 않은 경우를 구분하기 위해서'를 따로 설명하기 위함이다.

0번을 선택한 배열에선 마지막 스티커를 선택할 수 없기 때문에,
마지막 인덱스에 계산된 값(그림에서는 44)은 최대값 비교에 사용하지 않는다.
대신 뒤에서 2, 3번째인 34와 27이 그 대상이 된다.
이는 0번을 선택할 경우, 선택 가능한 스티커가 그 2개이기 때문이다.

1번을 선택한 배열에서는 그림에서 알 수 있듯 최대값으로 36을 가진다.

전체 배열에서 최대값의 후보들은 다음과 같다.

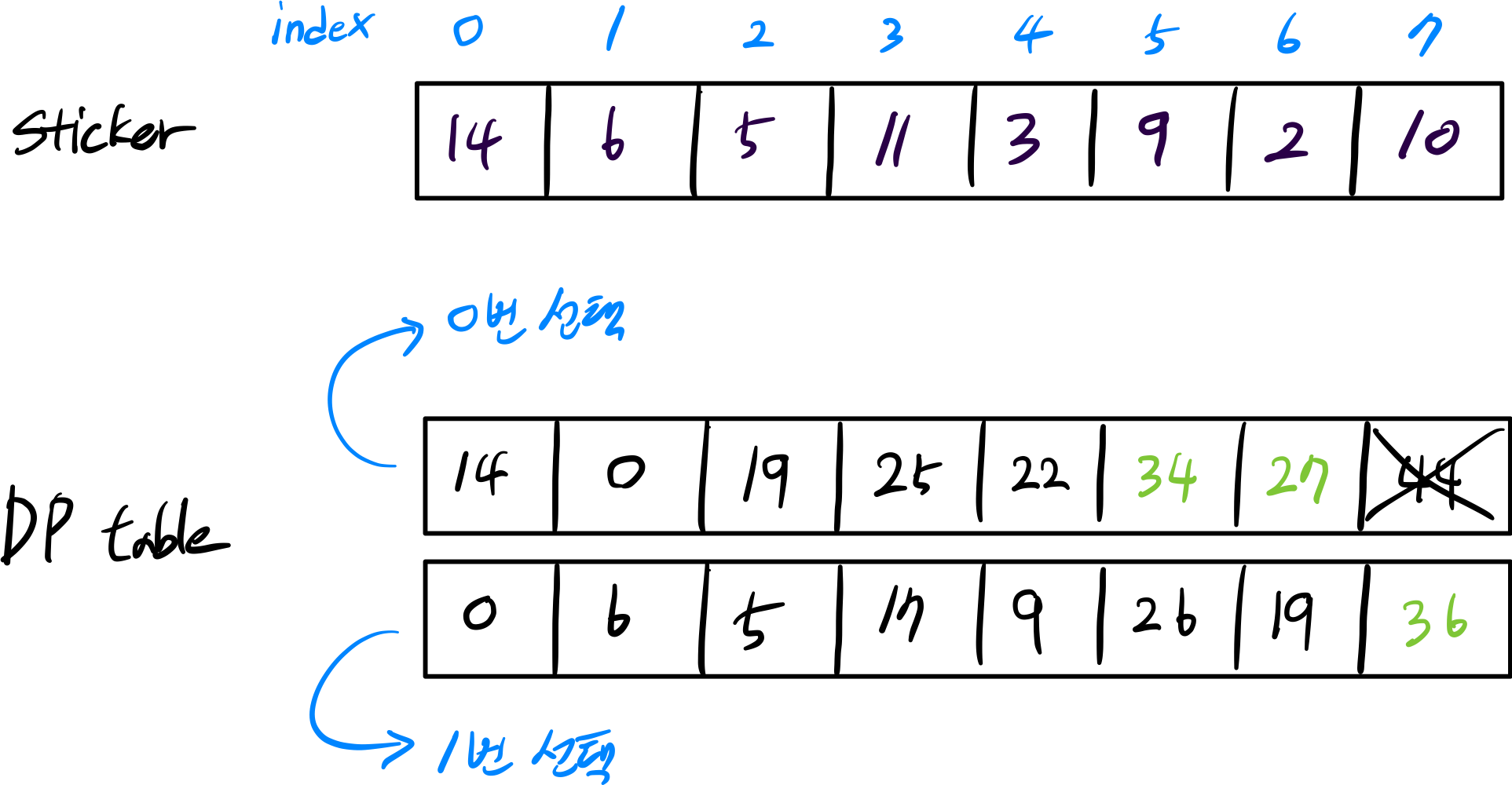
초록색으로 표시된 3개의 수 중 가장 큰 값인 36이 답이다.

코드

스티커 개수가 3개 이하인 경우에는 전체 스티커에서 하나만 선택 가능하기 때문에 조건문으로 분기했다.

def solution(sticker):
    answer = 0
    if len(sticker) <= 3:
        answer = max(sticker)
    else:
        dp = [[0] * len(sticker) for _ in range(2)]
        dp[0][0] = sticker[0]
        dp[1][0] = 0

        dp[0][1] = 0
        dp[1][1] = sticker[1]

        dp[0][2] = sticker[0] + sticker[2]
        dp[1][2] = sticker[2]

        for i in range(3, len(sticker)):
            dp[0][i] = sticker[i] + max(dp[0][i-2], dp[0][i-3])
            dp[1][i] = sticker[i] + max(dp[1][i-2], dp[1][i-3])

        answer = max(max(dp[0][-2], dp[0][-3]), max(dp[1]))
    return answer