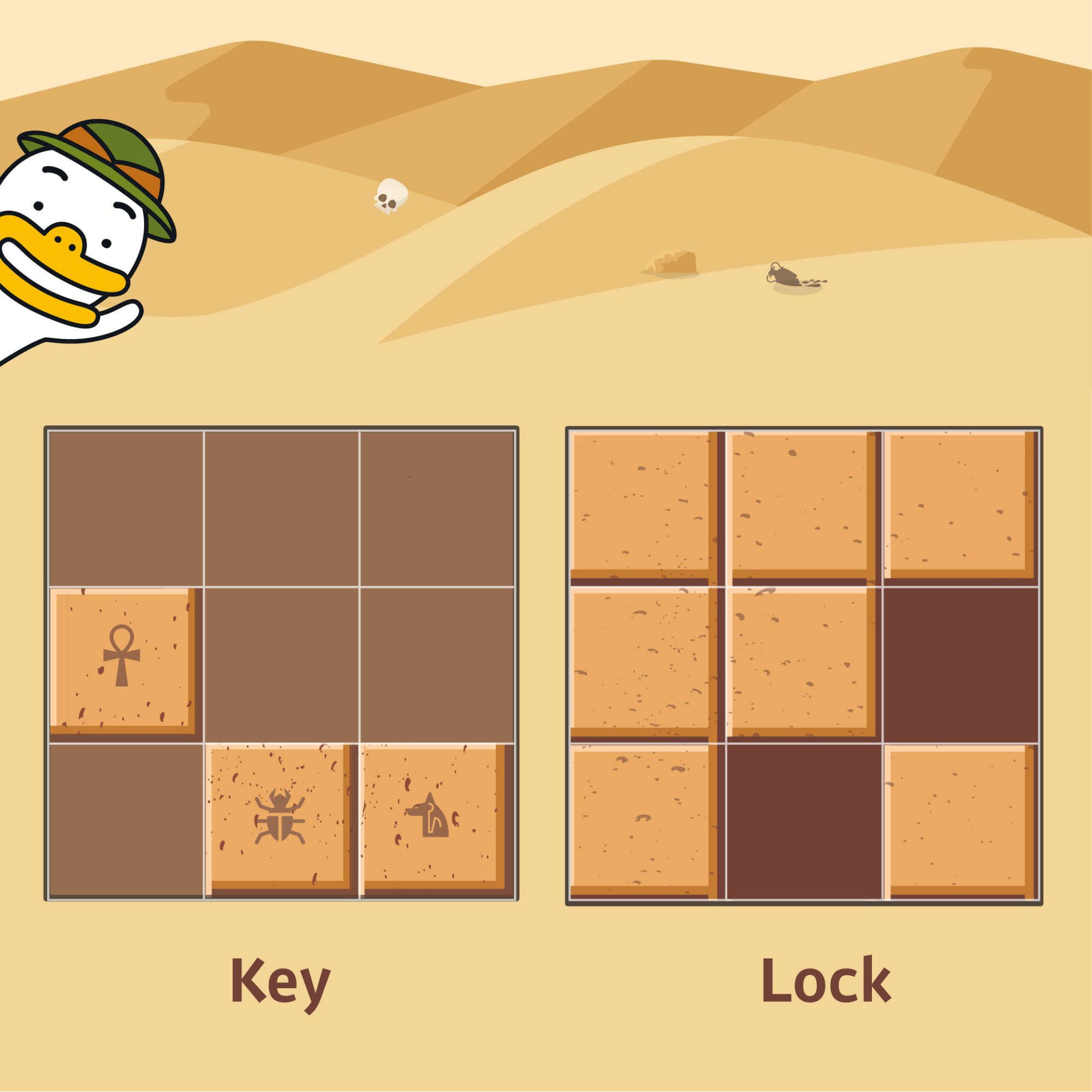
해당 문제는 프로그래머스에서 풀어볼 수 있기에 문제 자체는 생략하겠습니다.

문제 해결 방법

문제를 보자마자 떠오른 방법은

1. key 배열이 lock 의 배열 밖으로 넘어가 연산할 수 있어야하므로 lock 배열 자체를 len(key)-1 만큼 상하좌우로 늘려줍니다.
2. key 값을 rotate 시켜주며 늘어난 lock 배열에 넣어보기 즉 브루트포스입니다.
3. lv3 짜리 문제였고 이 정도문제가 브루트포스로 풀릴리 없을 거 같아 시간복잡도를 계산해 보았습니다.

시간복잡도를 먼저 계산해 제가 떠오른 방법이 맞는지 검증이 먼저 필요했습니다.

시간복잡도에서 탈락한다면 다른 방법을 떠올려야 했기 때문에 먼저 시간복잡도를 계산해줍니다.

배열의 크기가 최대 20x20 으로 크지 않지만, key 값이 lock 배열 밖으로 넘어가서 계산할 수 있기에 최대 계산 범위는 58x58 로 생각됩니다.

(key-1) x 2 만큼 앞뒤로 배열 연장시 19 x 2 + 20 = 58

58로 늘어났고 각 포인트마다 4번의 회전이 들어가 200 여번의 연산이 생각되고
회전 시 리스트 생성하는데 필요한 연산을 생각해보아도 연산량(시간복잡도) 자체는 문제가 될 거 같지 않았습니다.

이후 key array 값을 lock array 와 비교하는 최대 케이스의 연산량의 경우
58 x 58 x 20 x 20 x 4 = 5,382,400 번으로
백트래킹조차 필요하지 않는 1초이내 동작이 예상되었습니다.

저는 개인적으로 시간복잡도 문제를 생각해보았을때 문제 없을 것이라 판단하면 더 좋은 알고리즘이 있다해도 저는 바로 문제를 푸는 스타일입니다. 코테의 경우 시간이 남는 경우보다 부족한 경우가 많고, 문제를 넘어갔다가 다시 돌아 올 수 있기 때문에 만약 해당 문제가 찝찝하다면 표시 후 남은 시간에 풀어보면 되기 때문입니다.

문제 풀이

1. key 배열이 lock 의 배열 밖으로 넘어가 연산할 수 있어야하므로 lock 배열 자체를 len(key)-1 만큼 상하좌우로 늘려줍니다.

이건 자신의 취향대로 값을 늘려주면 될 거 같습니다. 저는 아래처럼 배열을 늘려주었습니다.

len(key) = 3, len(lock) = 3 이므로
최종적으로 늘어난 new_lock 의 array 는 (len(key)-1)x2 + len(lock) = 7
7x7 입니다.

    kn = len(key)
    prev_lock_zero = len(lock)+2*(kn-1)
    pb_lock = [[0] * prev_lock_zero for _ in range(kn-1)]
    new_lock = [p[:] for p in pb_lock]

    for line in lock:
        new_line = [0] * (kn-1) + line + [0] * (kn-1)
        new_lock.append(new_line[:])
    
    new_lock.extend(pb_lock)
    print(new_lock)
    
    ------
    출력:
    [[0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0], 
    [0, 0, 1, 1, 1, 0, 0], [0, 0, 1, 1, 0, 0, 0], 
    [0, 0, 1, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0], 
    [0, 0, 0, 0, 0, 0, 0]]

2. key 값을 rotate 시켜주며 늘어난 lock 배열에 넣어보기 즉 브루트포스입니다.

rotate 시키는 문제는 종종 나오므로 암기를 해두셔도 좋지만 저는 머리가 나빠 암기를 못하여 대충 그림을 한번 그려보고 원리를 파악 후 빠르게 그때그때 함수를 만드는 편입니다..

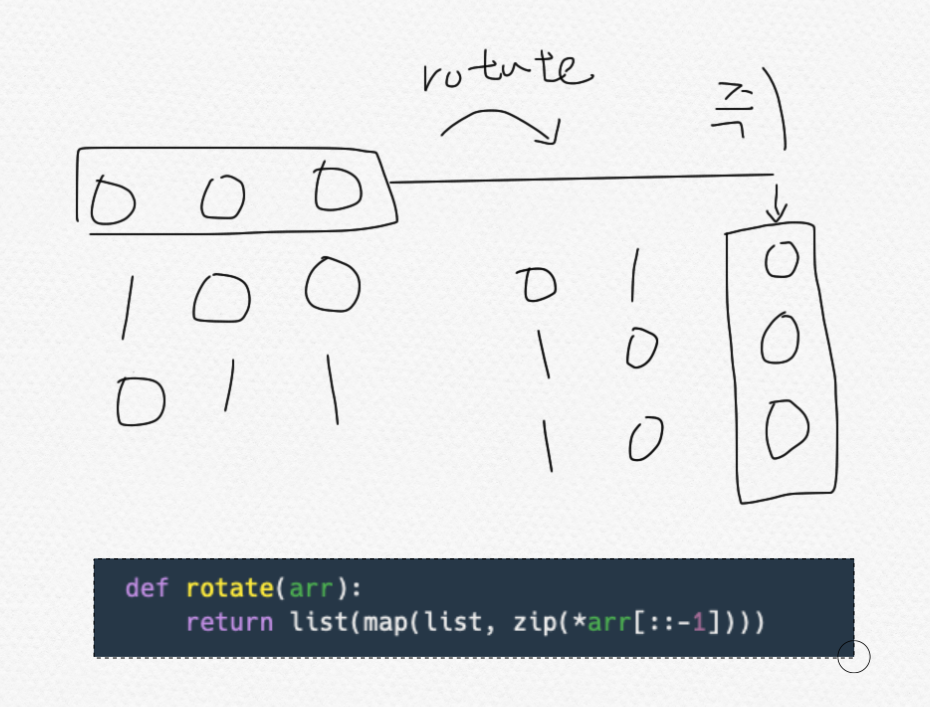
다음과 같이 그림이 그려지고 위 함수처럼 구현하면 될 거 같습니다.

최종 코드

def rotate(arr):
    return list(map(list, zip(*arr[::-1])))


def solution(key, lock):
    kn = len(key)
    prev_lock_zero = len(lock)+2*(kn-1)
    pb_lock = [[2] * prev_lock_zero for _ in range(kn-1)]
    new_lock = [p[:] for p in pb_lock]

    for line in lock:
        new_line = [2] * (kn-1) + line + [2] * (kn-1)
        new_lock.append(new_line[:])

    new_lock.extend(pb_lock)

    r90 = rotate(key)
    r180 = rotate(r90)
    r270 = rotate(r180)
    res = sum(l.count(0) for l in lock)

    for i in range(len(new_lock)-(len(key)-1)):
        for j in range(len(new_lock)-(len(key)-1)):
            for r in [key, r90, r180, r270]:
                cnt = res
                for k in range(len(r)):
                    for l in range(len(r)):
                        if new_lock[i+k][j+l] == 0 and r[k][l] == 1:
                            cnt -= 1
                        elif new_lock[i+k][j+l] == 1 and r[k][l] == 1:
                            cnt = 9999
                if cnt == 0:
                    return True

    return False

의식의 흐름대로 구현하여 예쁜 코드는 아니기에 부끄럽지만 간단한 문제는 간단하게 생각하고 푸는게 더 잘 풀리는 것 같습니다.

개인적으로 백트래킹도 아닌 단순 브루트포스로 lv3 치곤 쉬운편에 속하는 문제 같습니다.

하지만 확실히 카카오 문제들이 시각적 자료도 좋고 수학적인 문제보단 구현과 핵심 알고리즘을 아는지 물어보는 경우가 많아 재밌는 것 같습니다.

꾸준히 카카오 문제를 리뷰해보겠습니다.

문제를 풀며 배운점

List Comprehension(리스트 내포) 과 Generator Expression(제너레이터 표현식) 의 차이점을 명확히 이해는 계기가 되었습니다. 문제를 풀면서 둘의 차이가 있다는 점은 대충 알고 있었지만 명확히 설명하기 어려웠고 어떤 이점이 있는지 잘 몰랐습니다.

이번 문제를 풀며 0 갯수 카운트를 세며 Python 의 동작과정이 궁금하여 새롭게 공부한 내용을 공유합니다.

List Comprehension

리스트 내포(list comprehension)는 새로운 리스트를 간결하고 효율적으로 생성하는 방법입니다. 리스트 내포를 사용하면, 반복문을 한 줄로 작성할 수 있으며, 이는 코드의 가독성을 높여줍니다.

예를 들어, 2차원 배열에서 각 행의 첫 번째 요소를 추출하는 리스트 내포는 다음과 같습니다:

matrix = [
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]
]

first_elements = [row[0] for row in matrix]
print(first_elements)  # [1, 4, 7]

이 코드에서 first_elements는 matrix의 각 행의 첫 번째 요소로 이루어진 새로운 리스트입니다.

Generator Expression

반면에, row.count(0) for row in matrix는 리스트 내포가 아닌 제너레이터 표현식(generator expression)입니다. 이는 즉시 모든 값을 계산하여 리스트로 반환하는 것이 아니라, 필요한 시점에 값을 하나씩 생성하는 방식입니다. 이는 메모리 효율성을 높이는 데 유용합니다.

예를 들어, 제너레이터 표현식을 사용하여 2차원 배열에서 0의 개수를 세는 방법은 다음과 같습니다:

matrix = [
    [0, 1, 2, 0],
    [3, 0, 4, 5],
    [6, 7, 0, 0]
]

zero_count = sum(row.count(0) for row in matrix)
print(zero_count)  # 5

이 코드에서 row.count(0) for row in matrix는 제너레이터 표현식입니다. sum 함수는 이 제너레이터 표현식에서 값을 하나씩 가져와 더합니다. 이 방식은 메모리를 절약할 수 있지만, 리스트 내포와는 다르게 리스트 객체를 생성하지 않습니다.

차이점 요약

리스트 내포 (List Comprehension):

• 새로운 리스트를 만듭니다.
• 모든 값을 즉시 계산하여 메모리에 저장합니다.
• 문법: [expression for item in iterable]
• 리스트 내포 예시:

  list_comprehension = [row.count(0) for row in matrix]
  print(list_comprehension)  # [2, 1, 2]

제너레이터 표현식 (Generator Expression)

• 값을 하나씩 생성합니다.
• 필요할 때마다 값을 계산하므로 메모리 효율적입니다.
• 문법: (expression for item in iterable)
• 리스트가 아닌 제너레이터 객체를 반환합니다.
• 제너레이터 표현식 예시:

  generator_expression = (row.count(0) for row in matrix)
  print(list(generator_expression))  # [2, 1, 2]

두 예시는 동일한 값을 생성하지만, 리스트 내포는 리스트 객체를 반환하고, 제너레이터 표현식은 제너레이터 객체를 반환합니다. 제너레이터 객체는 필요할 때마다 값을 하나씩 생성합니다.

결론

리스트 내포와 제너레이터 표현식은 각기 다른 용도로 사용되며, 특정 상황에 맞게 선택하여 사용하는 것이 중요합니다. 메모리 사용량이 중요하지 않고 즉시 모든 값을 사용할 경우 리스트 내포를, 메모리 사용량이 중요하고 값이 필요할 때만 계산하고자 할 경우 제너레이터 표현식을 사용하는 것이 좋습니다.