[Python / 프로그래머스] 연습문제 올바른 괄호의 갯수 문제 풀이입니다. 이 글에는 최종적인 정답 코드가 포함되어있습니다.
해당 문제는 프로그래머스에서 풀어볼 수 있기에 자세한 문제 설명은 생략하겠습니다.
문제 해결 방법
괄호문제를 보면 가장 먼저 드는 생각은 스택입니다. 스택자료구조의 대명사로 괄호가 분류되는 이유는 다들 아시다시피 올바른 괄호를 구성하는데 스택자료구조처럼 닫힘이 먼저 나왔다면 반드시 스택안에 열림이 들어있어야하기 때문이며, 열림이 닫힘보다 먼저 스택을 빠져나와도 올바른 괄호라고 볼 수 없기 때문입니다.
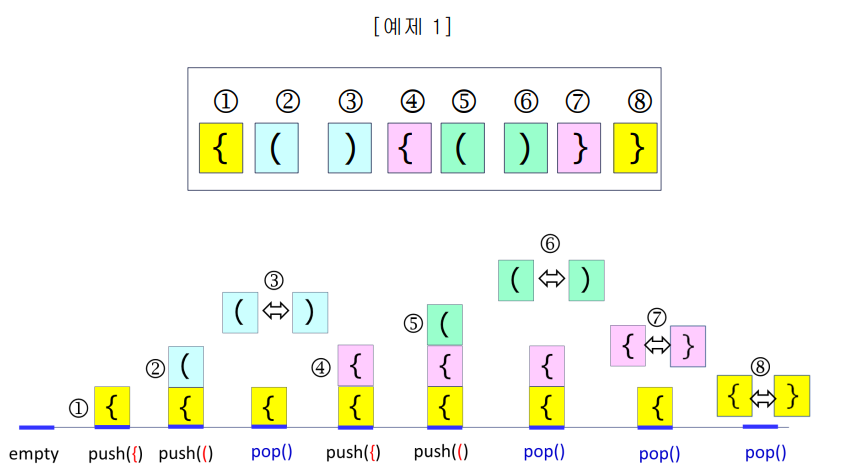
이렇듯 스택문제에 대해서 모든 경우의 수를 구하라는 스택 순열 문제의 경우 카탈란 수를 이용한 문제라고 볼 수 있습니다.
초기 카탈란 수를 모르고 문제를 풀어보았을 때 제가 접근했던 접근법은 괄호 1개를 타겟으로 하고 해당 괄호를 3가지 케이스로 분류해 모든 케이스를 체크해보려했습니다. 케이스는 다음과 같습니다.
괄호가 3개(n=3)일 때 나올 수 있는 경우의 수는 아래 5가지 입니다.
((())), (()()), ()()(), ()(()), (())()
그렇다면 n=4 일 때는 아래처럼 5*3 의 케이스를 가진다고 생각하였습니다.
- 예시 testCase (n=4)
- ()!{5가지}!
- (!{5가지}!)
- !{5가지}!()
그리고 그 중에서 겹치는 케이스인 2가지[()()()(), ()(())()] 케이스를 제외하면 13가지가 나올 수 있다고 판단하였습니다.
하지만 결과적으로 위 테스트케이스의 경우 한가지 체크가 안되는 지점이 있습니다. 바로 중간에 괄호가 닫히게 될 경우 확인이 불가능합니다.
ex) (())(())
이 문제를 해결하기 위해 괄호에 케이스 관리 중 첫번째 괄호 열림이 닫히는 지점에 대해서 관심을 가지게 되었습니다.
dp = [1, 1, 2, 5, ...]
- (){dp[3]} => 5가지 (dp[0] x dp[3])
- ((dp[1])){dp[2]} => 2가지 (dp[1] x dp[2])
- ({dp[2]})(dp[1]) => 2가지 (dp[2] x dp[1])
- ({dp[3]}) => 5가지 (dp[3] x dp[0])
총 14가지 케이스를 모두 체크할 수 있었습니다.
그리고 그 규칙을 발견 할 수 있었습니다.

이 규칙을 토대로 N:1, N:2 일 때도 확인해봄으로써 아래와 같은 점화식을 세울 수 있었습니다.
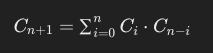
문제 풀이
이를 토대로 점화식을 세우고 간단하게 문제를 풀어보면 아래처럼 쉽게 문제 접근이 가능합니다.
# 카탈란수
def solution(n):
answer = 0
dp = [1, 1, 2, 5] + [0] * n
for i in range(3, n+1):
v = 0
for j in range(i):
v += dp[j]*dp[i-j-1]
dp[i] = v
return dp[n]마무리
카탈란 수를 모르고 문제를 풀게 된다면 DP 문제로 규칙이 안보이면 풀기 어려운 문제가 됩니다. 저도 항상 규칙을 발견하기까지 많은 시행착오와 시간이 소모되어 막상 코딩테스트에서 만나게되면 어려울 것 같습니다.
그러나 반대로 카탈란 수를 알고 문제를 보게된다면 해당 문제의 규칙을 알고 푸는 것이기 때문에 점화식을 아는 DP 문제가 됩니다. 다양한 DP 문제를 접하고 그 안에서 주로 사용되는 수학적 공식이나 점화식을 알아두는 것이 많은 도움이 될 것 같습니다.
추가적으로 카탈란 수의 경우 DP 를 사용하지 않으면 시간복잡도는 O(2^n)로 매우 풀기 어려워집니다. 이 문제의 경우 N <= 14로 풀이가 가능하지만 N이 50만 넘어가도 연산량이 1억을 가뿐히 넘어갑니다. 그렇기 때문에 DP로 O(N^3) 을 만들어야 풀 수 있는 다른 문제들도 같이 풀어보시면 좋을 것 같습니다.
