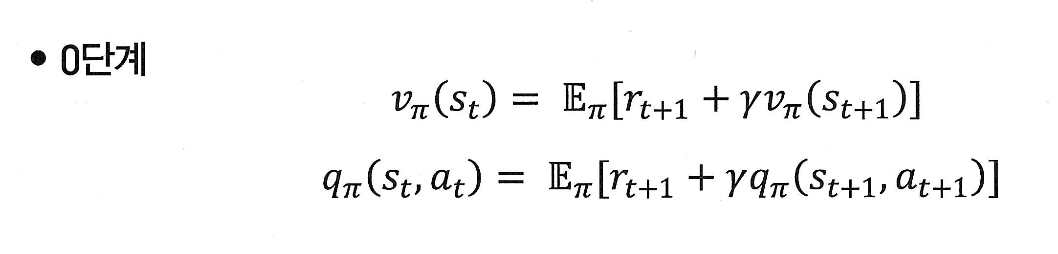벨만 방정식 : 특정 정책 π 하에서 각 상태(state)의 가치(Value)를 계산하기 위해 사용하는 핵심 수식이다.
0단계, 1단계, 2단계를 나눠 살펴볼 수 있다.
벨만 방정식
벨만 방정식 0단계
0단계 공식
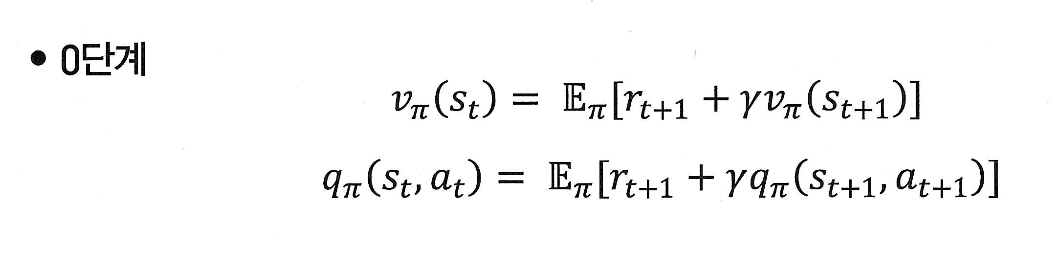
현재 상태 의 value란,
한 스탭 뒤에 받을 보상 과
그 다음 상태 에서의 를,
기대값(E) 형태로 더한 것이다.
( : 정책 𝜋를 따를 때, 현재 상태 에 있을 경우, 앞으로 받을 총 보상의 평균(기댓값)이다.)
=> 즉, 현재 상태 의 value는 다음 스텝에서 받을 보상 + 그 이후에 받을 총 보상의 평균(=미래 value)을 더한 것이다!
공식 유도
처음에는 이렇게 정의 되는데,
이 식을 재귀적으로 묶으면,
이렇게 된다.
기댓값이 필요한 이유
지금 강화학습에서는 미래에 어떤 일이 일어날지 정확히 모른다. 그래서 '평균적으로 이럴 것이다'라고 기대값(E)으로 계산해야 한다!
벨만 방정식 1단계
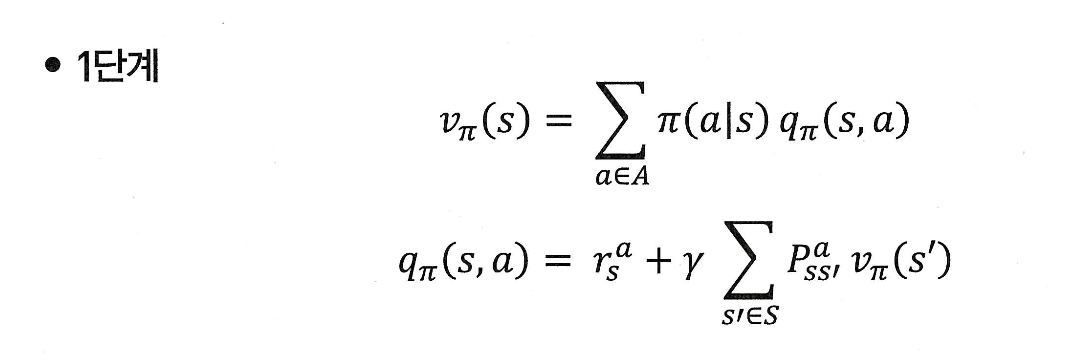
좋습니다! 지금 다루신 내용은 **벨만 기대 방정식 1단계 (Action-Value 기반)**이며, 크게 두 가지 핵심 식으로 구성되어 있습니다:
1) q -> v 계산
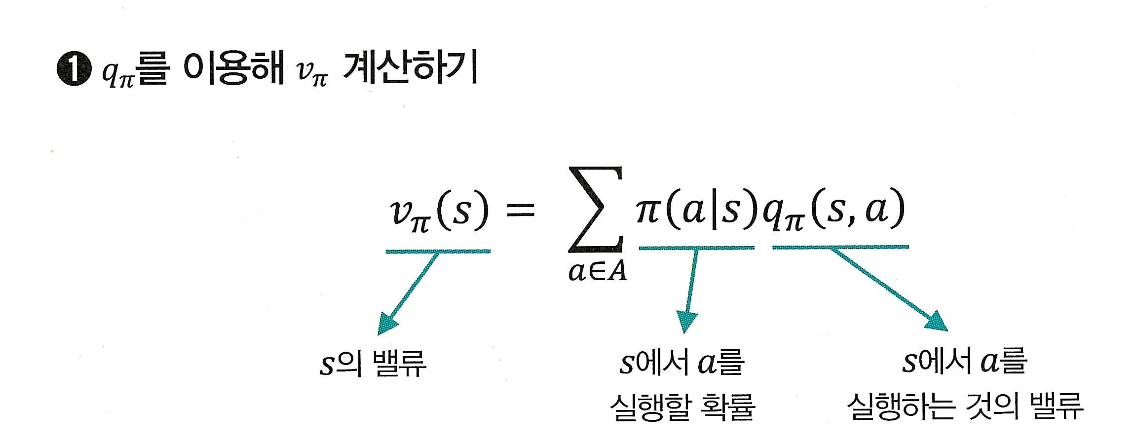
상태 의 value는, 그 상태(s)에서 어떤 액(a)션을 선택할지의 확률 와,
해당 액션을 실행했을 때의 가치 를 곱한 후,
모든 액션에 대해 평균(기댓값)을 낸 것이다!
예시)
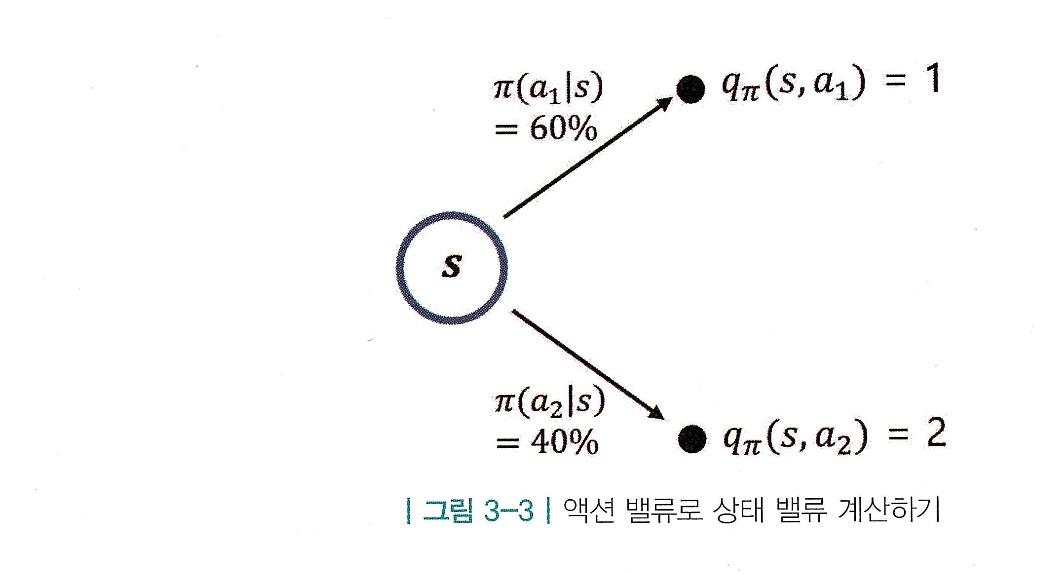
-
정책:
- ,
-
액션 가치:
- ,
→ 상태 가치:
2) v -> q 계산
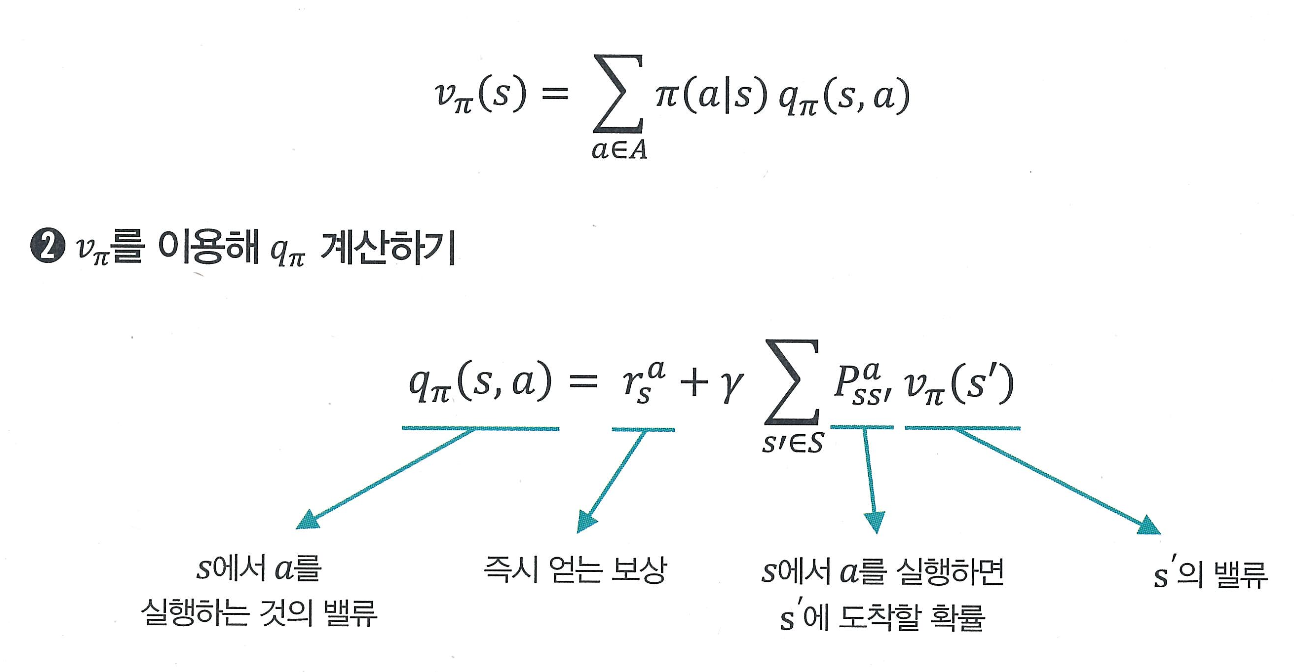
어떤 상태 에서 액션 를 실행하면 즉시 얻는 보상 와,
다음 상태 로 갈 확률 * 그 상태의 value 의 기대값
이 둘을 합친 것이 이다.
예시)
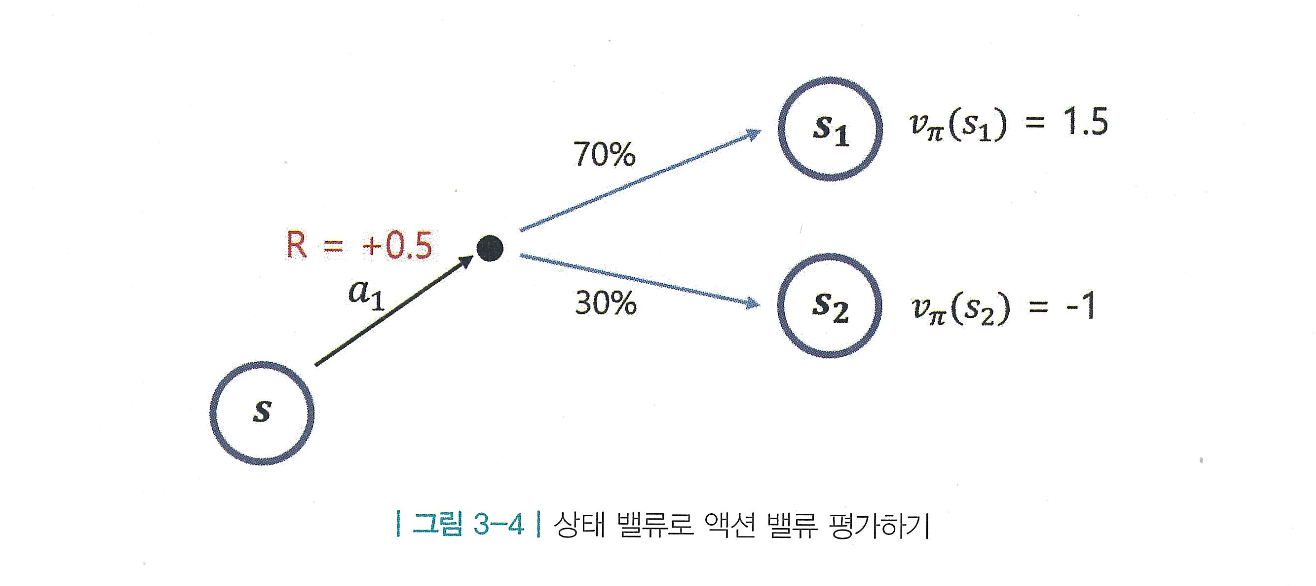
-
를 실행했을 때:
- 즉시 보상:
- : 확률 0.7,
- : 확률 0.3,
→ 액션 가치:
벨만 방정식 2단계
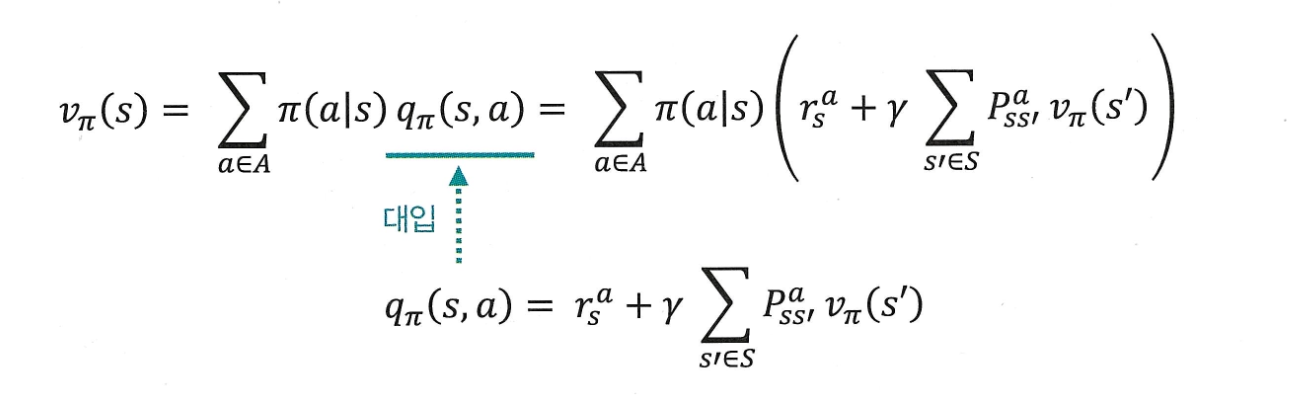
1단계 수식들을 그냥 대입만 하면 된다!
최종 수식
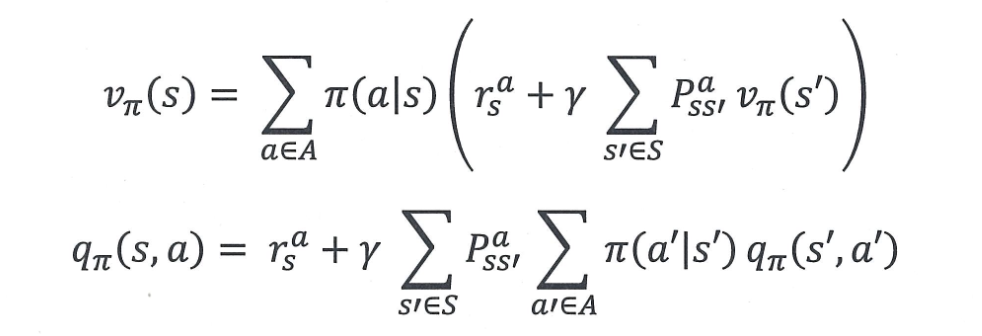
현재 상태의 가치는,
그 상태에서 어떤 행동을 할지 정한 후,그 행동으로 어떤 결과가 일어날지 고려해서
평균적으로 받을 보상을 계산한 값이다!
0단계와 2단계의 차이
0단계가 미래 보상에 대해 기대값(E)만 있다면, 2단계는 그 기대값을 확률과 가치로 풀어 썼다. (직접 계산 가능)
즉, 2단계는 기대값을 계산 가능한 형태로 완전히 전개한 식으로, 모델을 안 다면 이 수식만으로도 계산이 가능하다!
용도 구분
모델 기반 - 2단계 - r, P를 알고 있는 경우, 시뮬레이션만으로도 학습이 가능하다.
모델 프리 - 0단계 - r, P를 모르는 경우, 직접 행동하며 경험 기반 학습이 필요하다.
**현실 세계에서 강화학습할 때 대부분 모델 프리 상황이지만, 2단계 수식은 MDP 전체 구조를 수학적으로 가장 명확하게 설명해주는 식이다!
벨만 최적 방정식
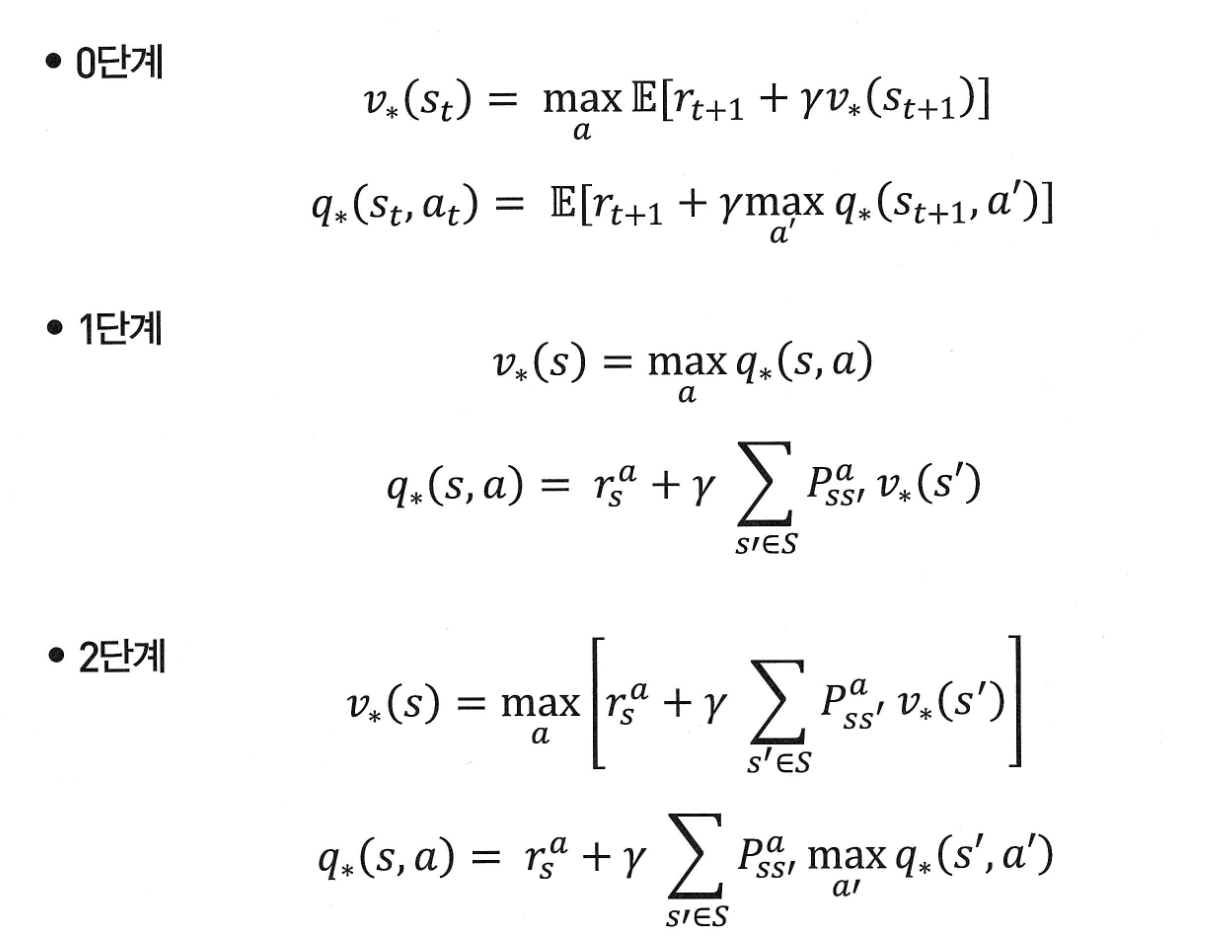
기존 벨만 방정식은 현재 상태의 value를 미래의 기댓값으로 표현한다. 하지만 이 방식은 정책이 고정되어 있을 때만 사용할 수 있다는 한계가 있다.
따라서 더 나은 정책을 찾기 위해 기대값이 아닌 가장 큰 value를 줄 수 있는 액션만 선택하는 방식의 벨만 최적 방정식이 등장하게 되었다!
0단계
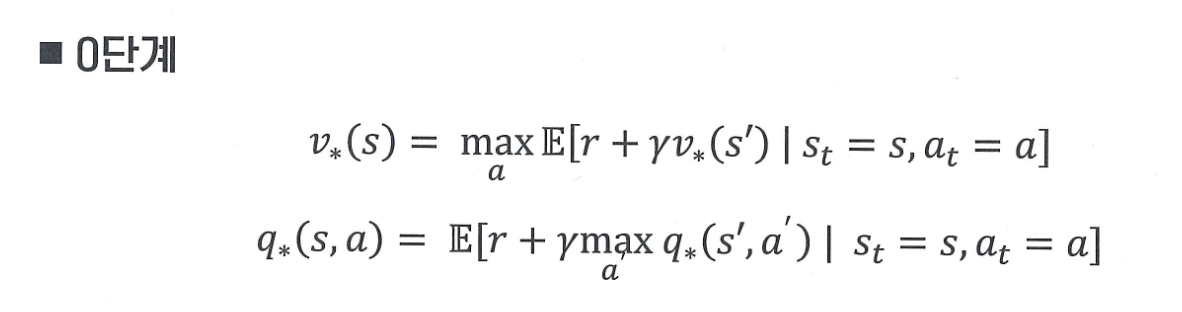
앞서 말했듯 기존 벨만 방정식은 고정된 정책에서만 사용 가능하였다. 그래서 최적의 정책을 찾고자 할 때, 기댓값(E) 대신, 최댓값(max) 연산으로 확장된 것이 벨만 최적 방정식이다!
즉, 최적 상태 가치 는 가능한 모든 액션 중에서 보상 + 미래 가치의 기대값이 가장 큰 액션을 선택했을 때의 기대 보상이다.
1단계
q -> v 계산

상태 s 의 최적 밸류는 s 에서 선택할 수 있는 액션들 중에 밸류가 가장 높은 액션의 밸류와 같다는 뜻이다.
쉽게 말해서, 지금 상태에서 할 수 있는 행동들 중 앞으로 가장 이득이 클 행동 하나를 고른다면, 그 행동이 주는 가치가 이 상태의 최적 가치라는 것이다!
벨만 포드 방정식과 다른 점은 더 이상 확률 π(a∣s)을 고려하지 않는다. 왜냐하면 최적 정책은 항상 가장 좋은 액션만 100% 선택하기 때문이다!
v -> q 계산
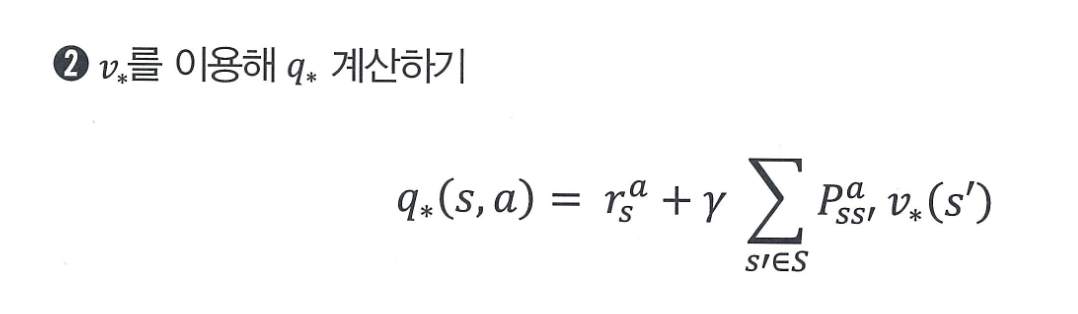
특정 상태 s에서 액션 a를 선택하면,
- 해당 액션에 따른 즉시 보상 를 받고
- 전이 확률 에 따라 다음 상태 로 이동하며
- 그 상태의 최적 가치 를 반영해
- 전체 기대 보상(즉, )을 계산한다!
이는 기존 벨만 방정식 1단계와 형태는 같지만, 정책에 따른 확률 평균 대신 항상 최적 행동만 고려한다는 점이 다르다!
2단계
2 단계 수식 또한 벨만 기대 방정식 때와 마찬가지로 1단계의 수식 2개를 조합
하여 만들 수 있다. 의 식에 의 식을 대입하면 끝이다!
1) 상태 가치 계산
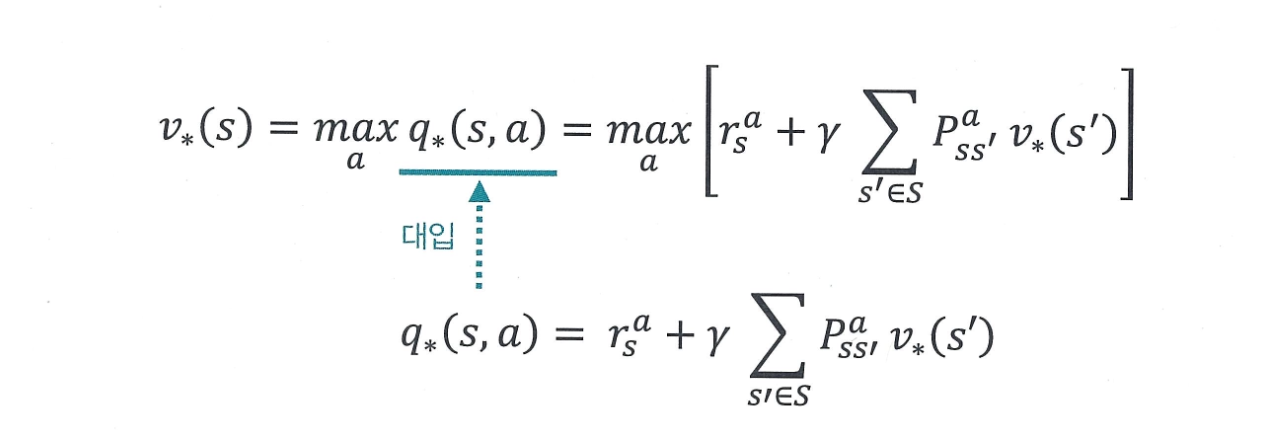
어떤 상태 에서 가능한 모든 액션 중에서,
- 즉시 보상 와
- 다음 상태 로 전이될 확률 ,
- 그 상태의 최적 가치 의 기대값
을 모두 계산한 뒤, 그 중 가장 큰 값을 주는 액션을 선택했을 때의 기대 보상이 바로 이다.
2) 액션 가치 계산
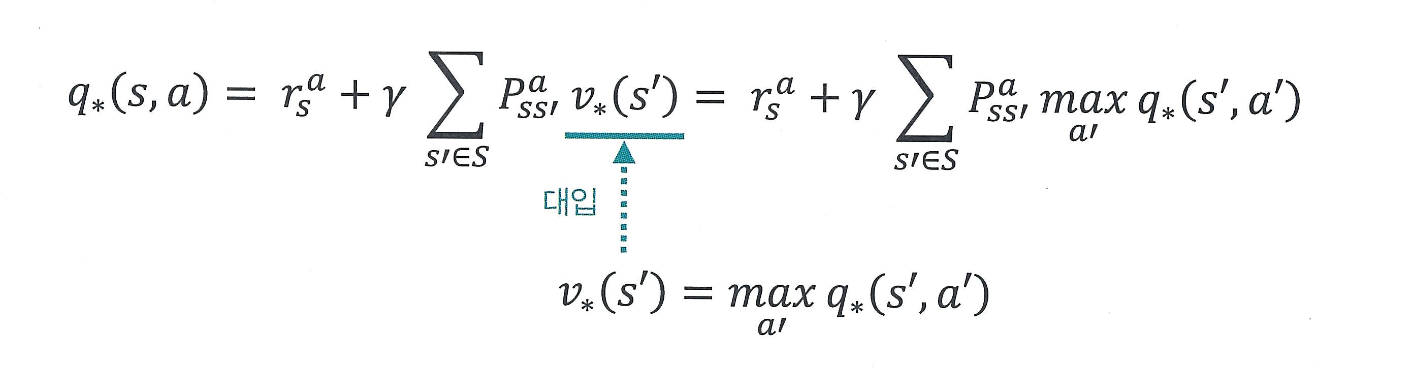
특정 상태 에서 액션 를 선택했을 때,
- 즉시 보상 를 받고
- 다음 상태 로 갈 확률에 따라
- 그 상태에서 가장 좋은 액션을 선택했을 때의 기대 보상까지 고려한 값이
바로 현재 상태-행동 쌍의 최적 가치 이다.
요약하자면,
- 는 "어떤 액션을 했을 때 가장 좋은가"에 대한 상태 단위 평가이고,
- 는 "특정 액션을 했을 때 얼마나 좋은가"에 대한 상태-행동 단위 평가이다.
그래서 이 두 수식은 서로를 통해 재귀적으로 계산 가능하며, 결국 최적의 정책을 찾는 데 사용된다고 한다!
추가적으로,
는, “이 상태에서 이 행동을 하면 얼마나 좋을까?”와 같은 하나의 행동 단위 평가이고,
(ex, 김치찌개를 먹기라는 행동의 총 기대 가치)
는 “이 상태 전체에서 평균적으로 얼마나 좋을까?”와 같은 상태 단위, 즉 여러 액션들을 모두 고려한 요약된 가치이다.
(ex) 이 가게에서 내가 뭘 먹을지를 고려한 전체 기대 만족도)
출처 - 바닥부터 배우는 강화 학습