기본미션
Ch. 04(04-1) 2번 문제 풀고, 풀이 과정 설명하기
- 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
✔1) 시그모이드 함수
2) 소프트맥스 함수
3) 로그 함수
4) 지수 함수
로지스틱 회귀(Logistic Regression)
우선 문제를 이해 하기 위해서 로지스틱 회귀(Logistic Regression)가 무엇인지 이해해야 한다.
회귀를 사용하여 데이터가 어디에 속하는지 분류하는 것이다. 이름에 회귀가 있어서 회귀로 착각할 수 있지만, 결론적으로 회귀를 이용해서 분류를 한다는 의미이다.
기본적으로 특징을 이용하여 선형회귀에 적용한다면. 책의 예시처럼
각 특징이 반영된 1차 함수의 각 계수 값(a..e)과 가중치 값(f)을 찾아 낼수 있겠지만
z = a * (Weight) + b * (Length) + c * (Diagonal) + d * (Height) + e * (Width) + f대략적인 선형 함수의 모양이 아래와 같아서 확율로 판단하기 난해한 구간도 발생한다.
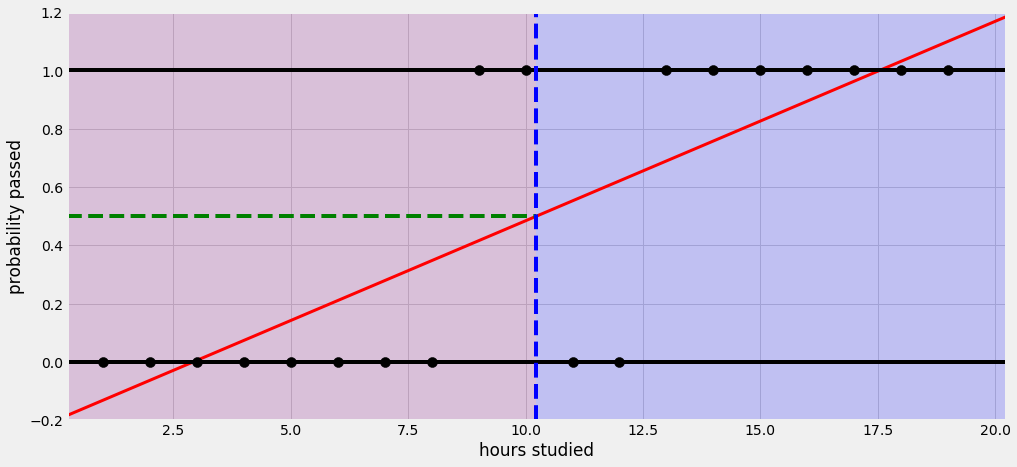출처 - https://hleecaster.com/ml-logistic-regression-concept/
확율을 통하여 분류를 하기위하여 시그모이드(sigmoid)함수(또는 로지스틱 함수)를 이용하면 0~1내의 값으로 확률로서 판단되기 때문에 특정 입력에 대하여 확율을 통하여 2진(이것이 맞냐, 틀리냐) 분류할 수 있다.
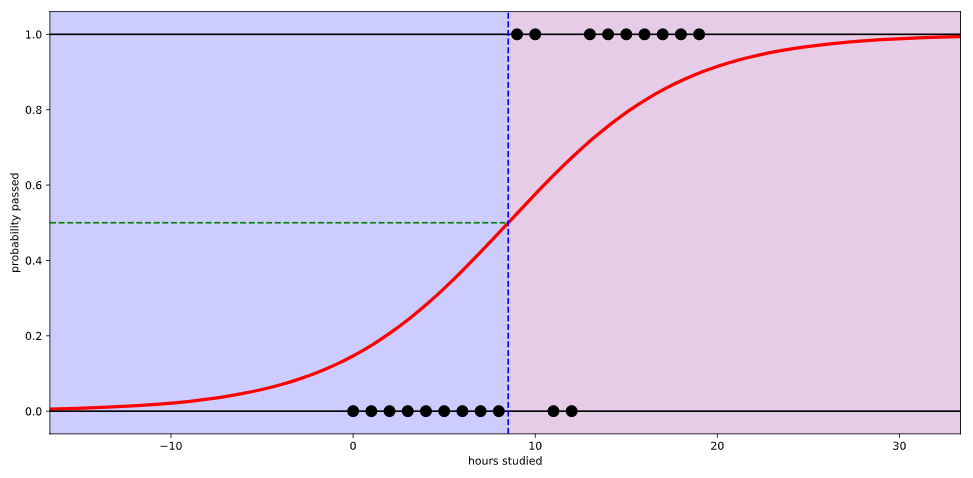출처 - https://hleecaster.com/ml-logistic-regression-concept/
참고. 시그모이드 함수의 수학식의 코드 표현 (책 참조)
1/(1+np.exp(-z))문제는 2진 분류이기 때문에 sigmoid로 분류 가능하다. 하지만 다중 분류인 경우 N개의 시그모이드를 통과해서 나오는 값이기 때문에 softmax를 한번더 돌려줘야 전체 합이 1인 확율로 표현할 수 있다.
선택미션
Ch.04(04-2) 과대적합/과소적합 손코딩 코랩 화면 캡쳐하기
개발자