벡터(Vector)
선형대수학을 위한 벡터란?
-
벡터(vector): 크기(magnitude)와 방향(direction)을 동시에 나타냄

-
2차원 뿐만 아니라 3, 4, 5, 6차원 이상으로 확장 가능
-
벡터는 크기와 방향만 신경쓰면됨, 어디서 시작하는지, 어디에 표현하는지 상관 없음
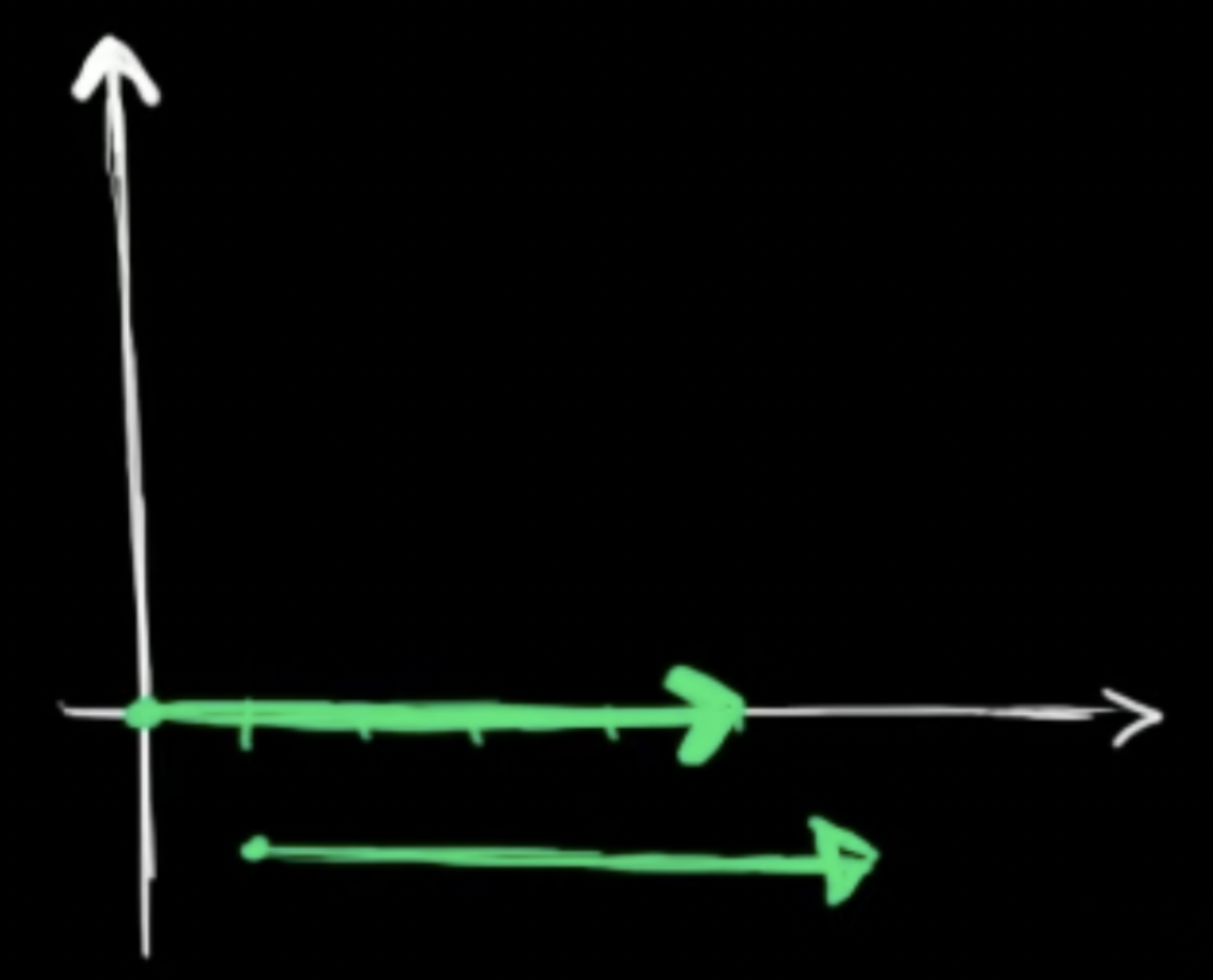
- 둘이 같음
-
수식으로 표현

- 첫번째 좌표: 수평으로 얼마나 움직엿는지
- 두번째 좌표: 수직으로 얼마나 움직였는지
-
다른 예시
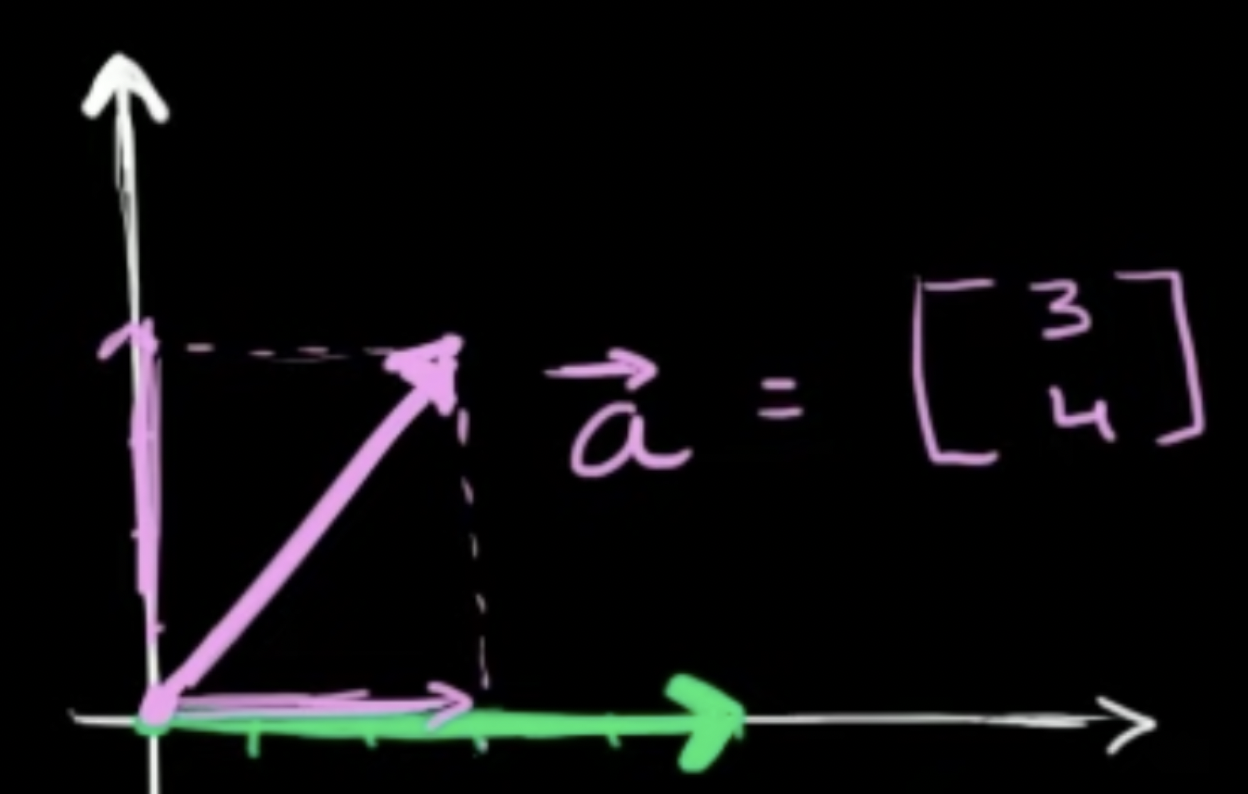
- 피타고라스 정리를 통해 벡터의 길이를 구할 수 있음 (magnitude: 5)
실좌표공간 (real coordinate space)

-
R: 실수좌표공간임을 의미, 2: 다루는 차원을 의미
- 2차원 실수좌표공간은 실수값을 가진 모든 2-tuple을 말함
- R^2를 다룬다는 것은 모든 가능한 실수값을 가지는 2-tuple을 다루는 것
- 영벡터(0,0): 크기는 없고 방향은 정해지지 않음
- 모든 2-tuple에 대해서 벡터들을 조합하여 2차원 실수좌표공간도 만들어낼 수 있음
-
튜플(tuple): 순서가 정해진 숫자들의 리스트
- 2-tuple: 숫자 2개의 순서리스트, 실수 2개의 순서리스트
-
R^3: 3차원 실수좌표 공간, 가능한 모든 실수값을 가지는 3-tuple 이용 가능
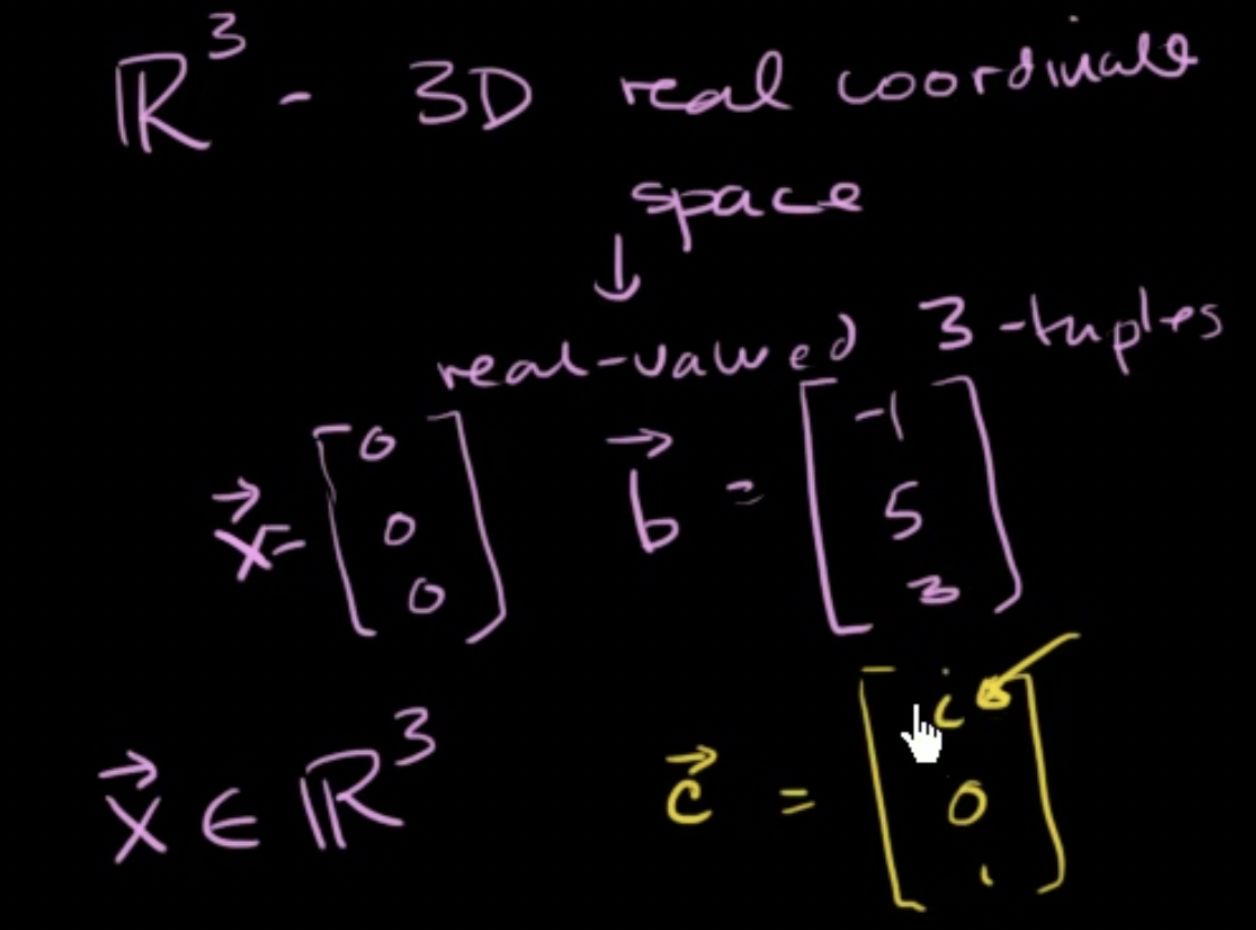
- x벡터와 b벡터는 R^3라는 집합의 원소
- 허수 성분을 가진 벡터는 R^3상의 벡터가 아님
대수와 그래프를 이용한 벡터의 덧셈
- 대응하는 값을 서로 더함, 벡터의 순서를 바꾸어도 같음
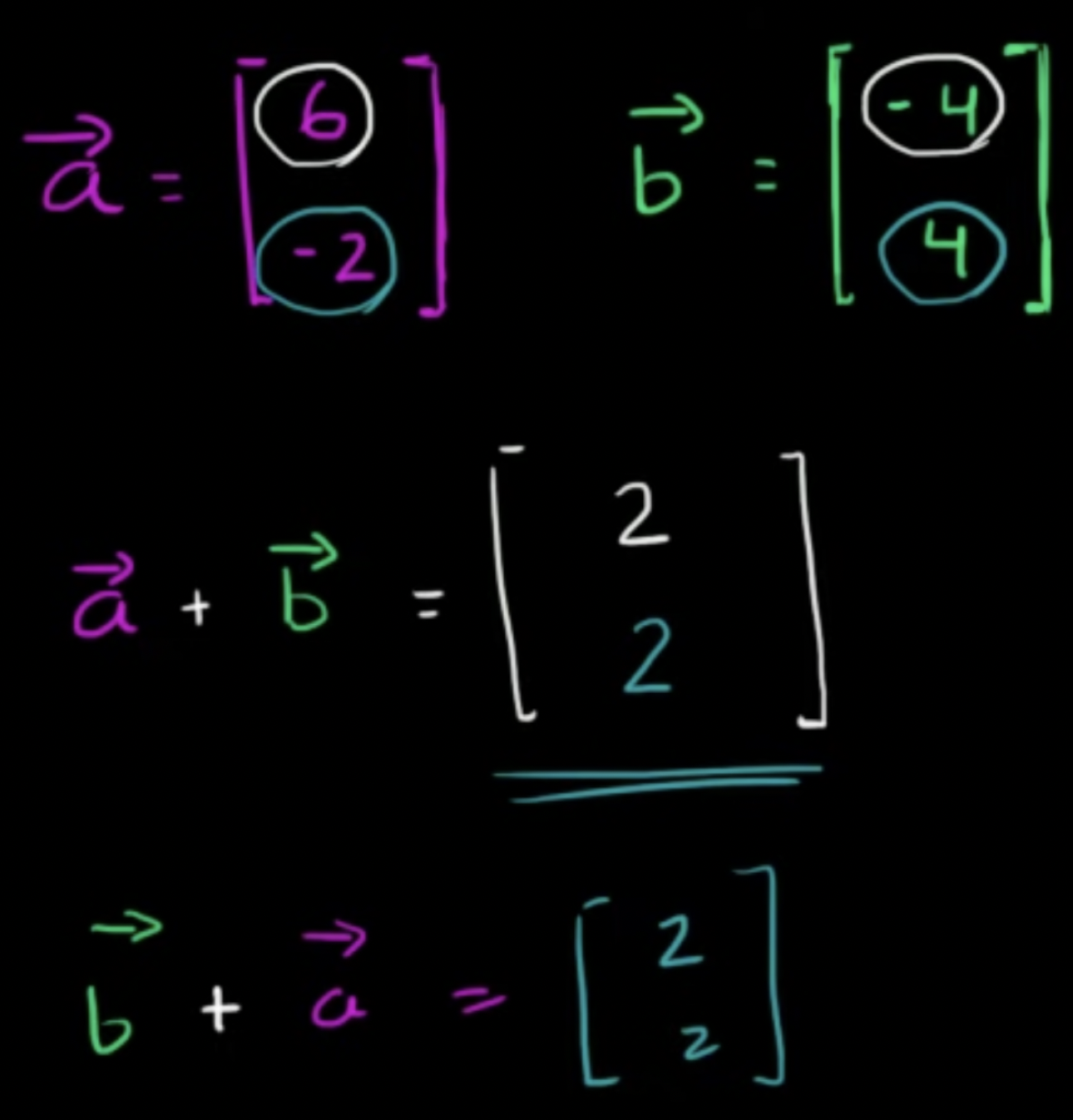
- 시각적으로 표현: 벡터 a가 간 곳에서 벡터 b의 꼬리를 거기에 두면 벡터합인 파란색 벡터의 머리까지 가게 됨
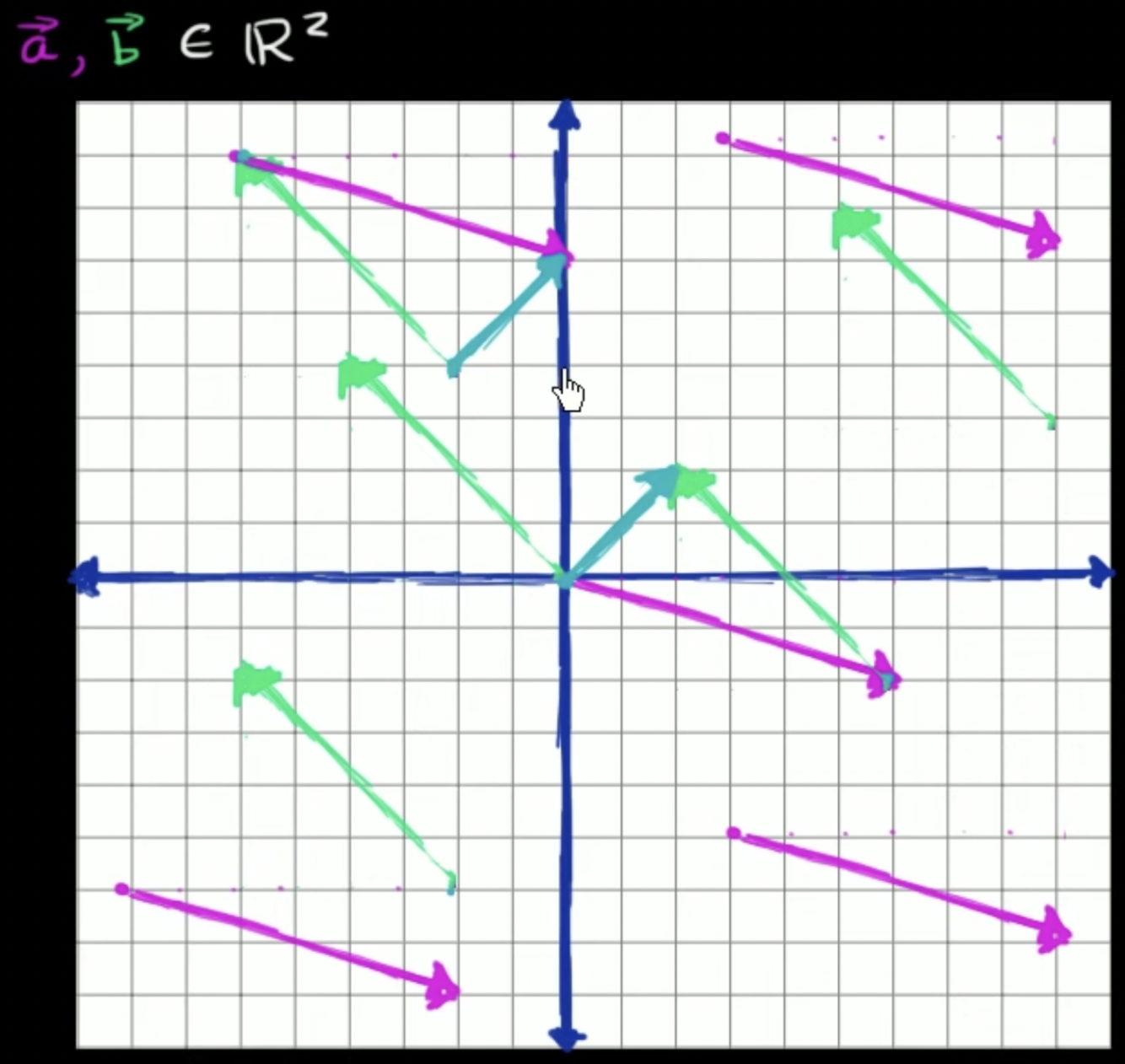
- 크기: 벡터의 길이, 방향: 벡터가 가리키는 방향
벡터와 스칼라의 곱셈
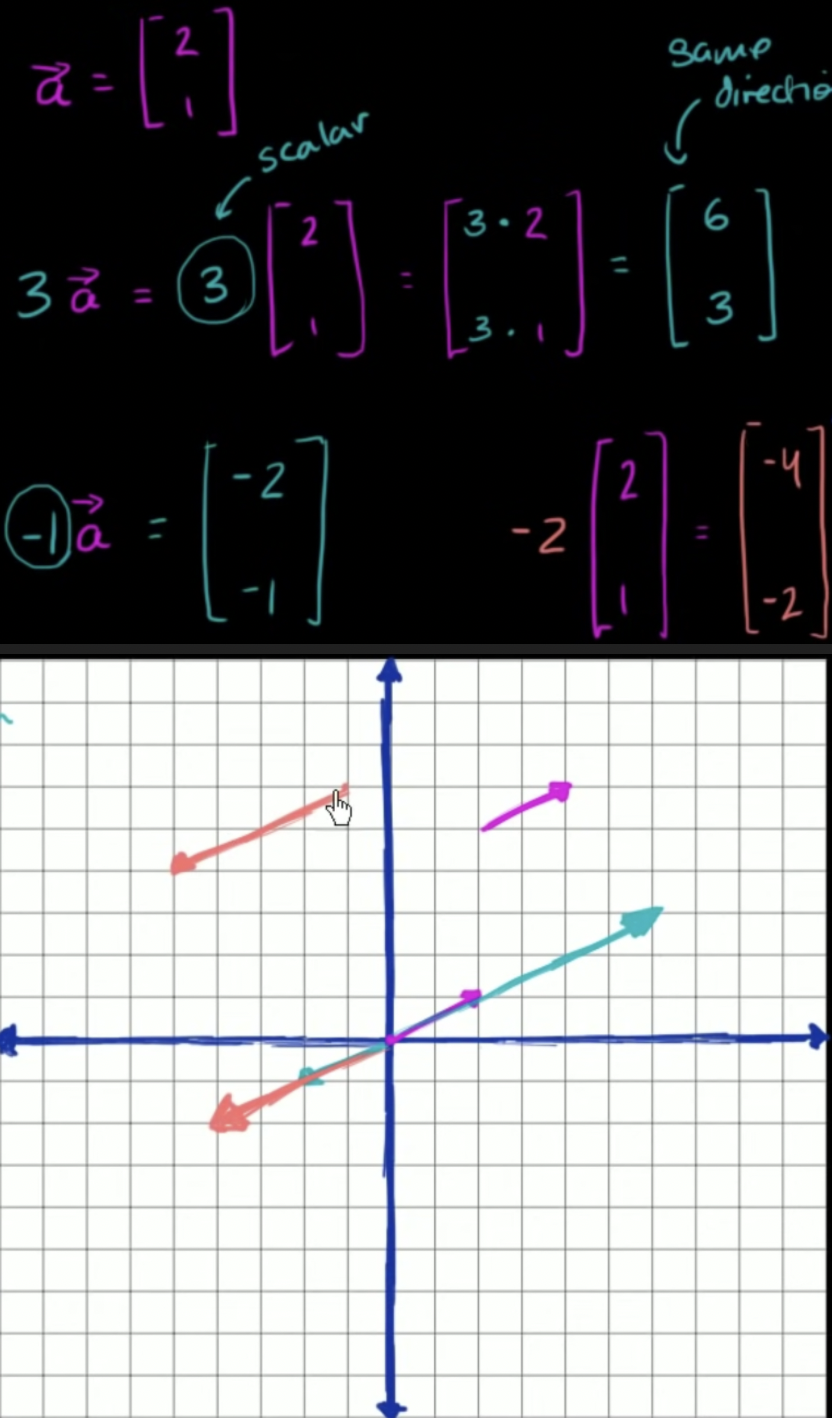
- 벡터의 각각의 성분에 스칼라를 곱해줌, 여전히 2차원 벡터
- 벡터의 방향은 변하지 않고 크기만 변함
- 스칼라만큼 확대됨, scalar, scale up(확대)의 어원은 같음
- 스칼라의 곱은 벡터를 확대함
- 벡터에 음수를 곱하면 방향은 완전히 반대로 됨
- 마이너스 부호가 벡터의 방향을 뒤집고 스칼라 값만큼 크기를 키움
벡터 예제
- 벡터는 어떤 점에서든 시작할 수 있음
- 보통 벡터의 시작점은 표준점(standard position)(0,0)
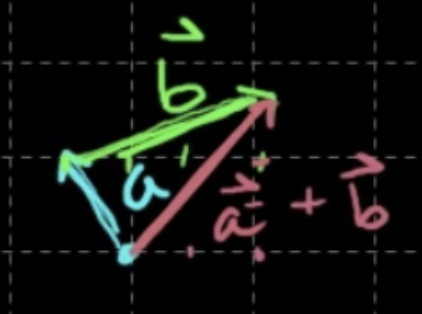
- 벡터의 합(벡터 a + 벡터 b) : 벡터 b의 꼬리를 a의 머리에 연결, a의 시작점과 b의 끝점을 연결
- 스칼라 곱: 벡터의 방향은 변하지 않고 길이만 배가 됨
- -(마이너스) 곱: 정반대의 방향으로 변함
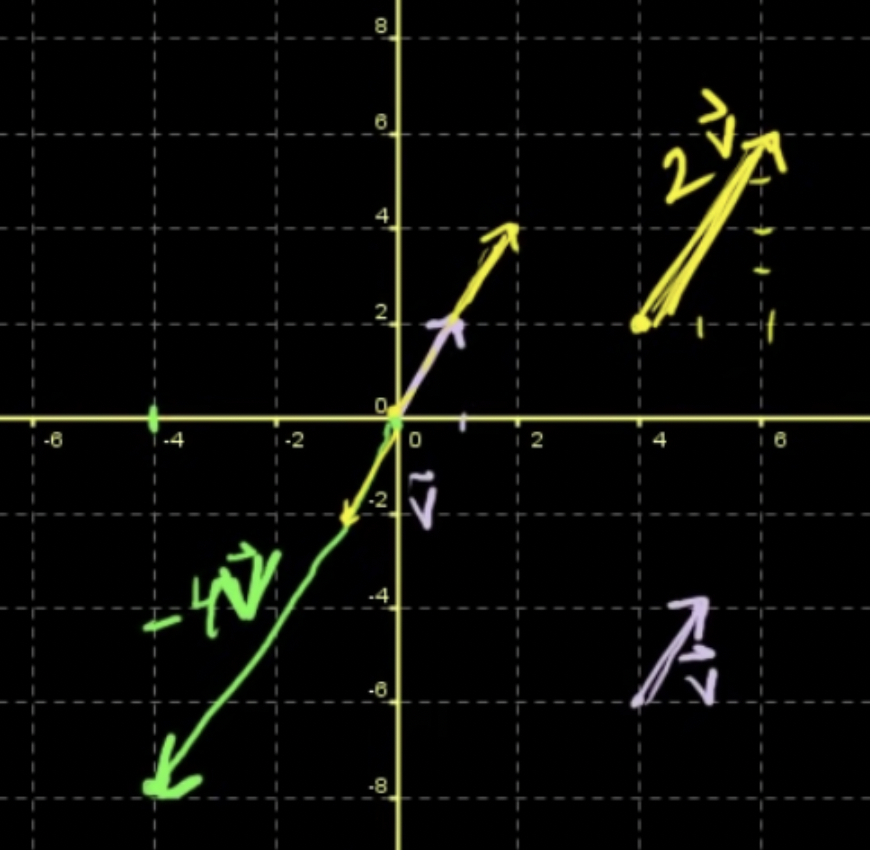
- -(마이너스) 곱: 정반대의 방향으로 변함
- 벡터의 차 (subtracting vectors): x - y = x + (-1 * y)
- 벡터 y에 (x-y)를 더하면 벡터 x
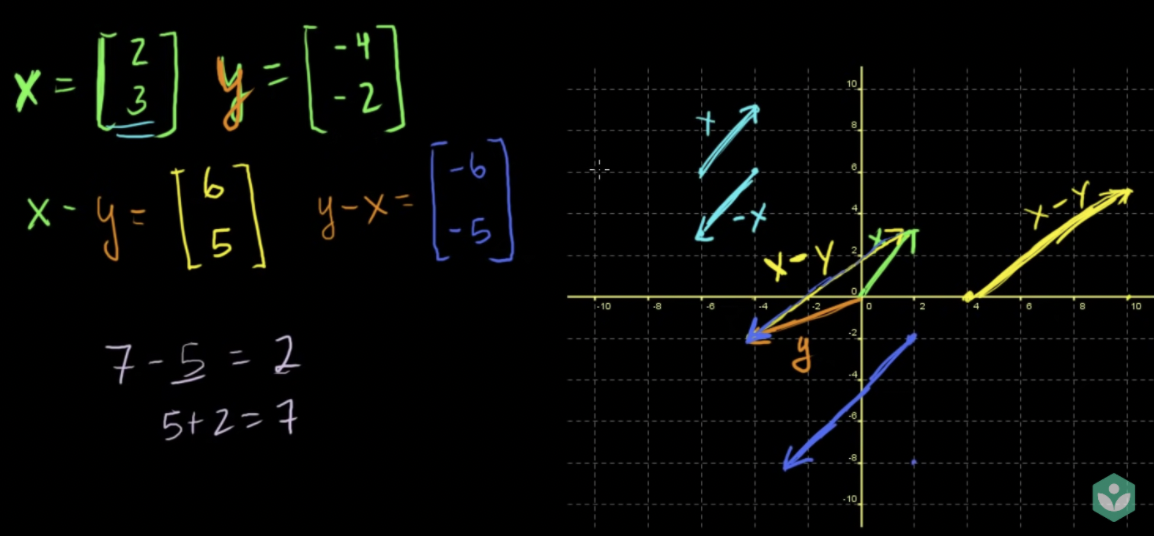
- 벡터 y에 (x-y)를 더하면 벡터 x
단위 벡터(Unit Vector)란?
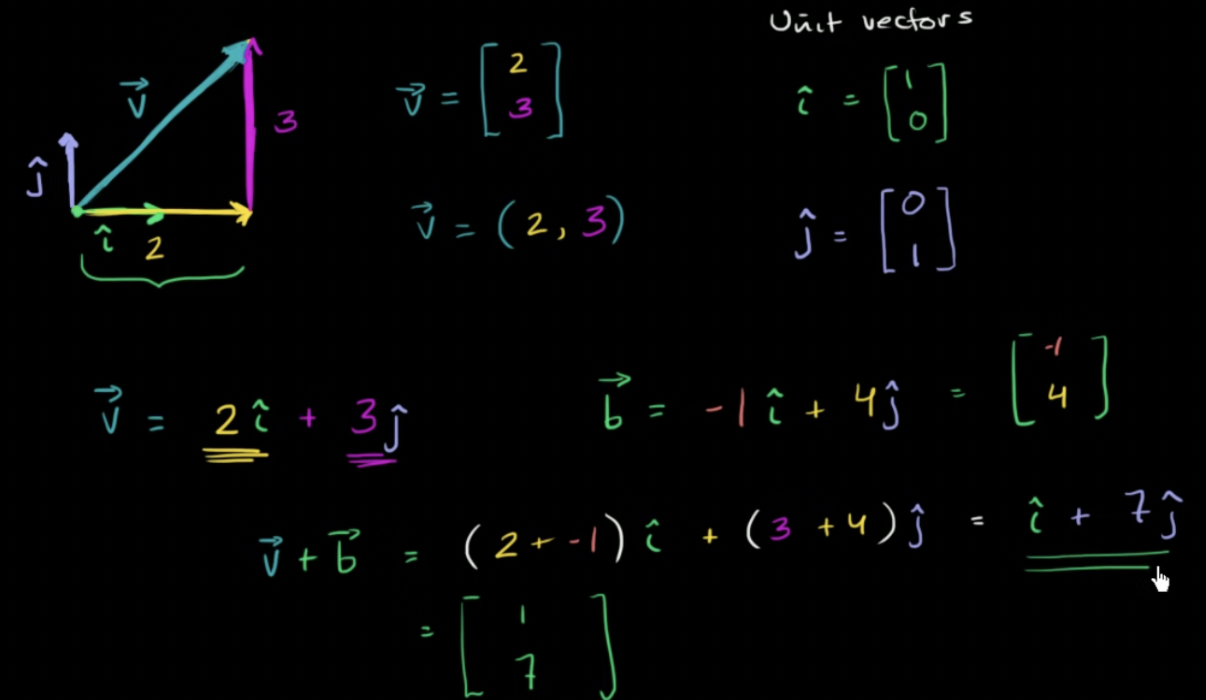
- 단위 벡터의 표현: 위에 ^을 씌움
- 단위 벡터: 크기가 1인 벡터
- 단위 벡터 값 각각을 제곱하여 더하면 합은 1
- 단위 벡터 i: 수평으로 1단위만큼 이동, 수직으로는 이동 x
- 단위 벡터 j: 수직으로 1단위만큼 이동, 수평으로는 이동 x
- 어떤 2차원 벡터든 i와 j의 합으로 표현할 수 있음
직선의 매개변수 표현
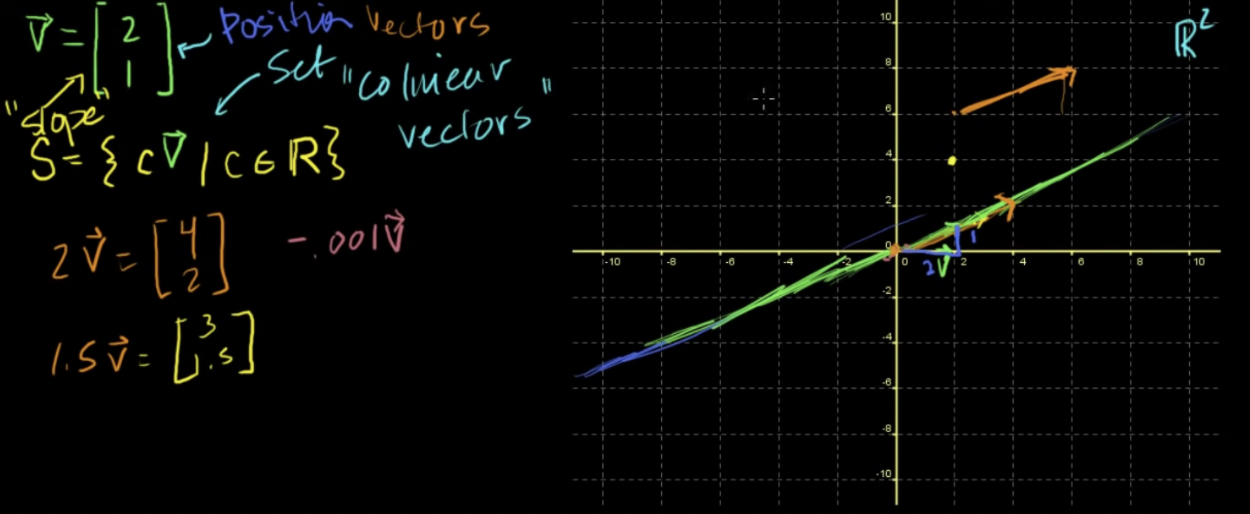
- 만들 수 있는 모든 벡터의 집합을 정의하면, 동일선상에 존재하는 벡터의 집합으로 시각화할 수 있음 (colinear vectors)
- 같은 기울기를 가진 다른 직선을 표현하고 싶다면 다른 벡터를 더함
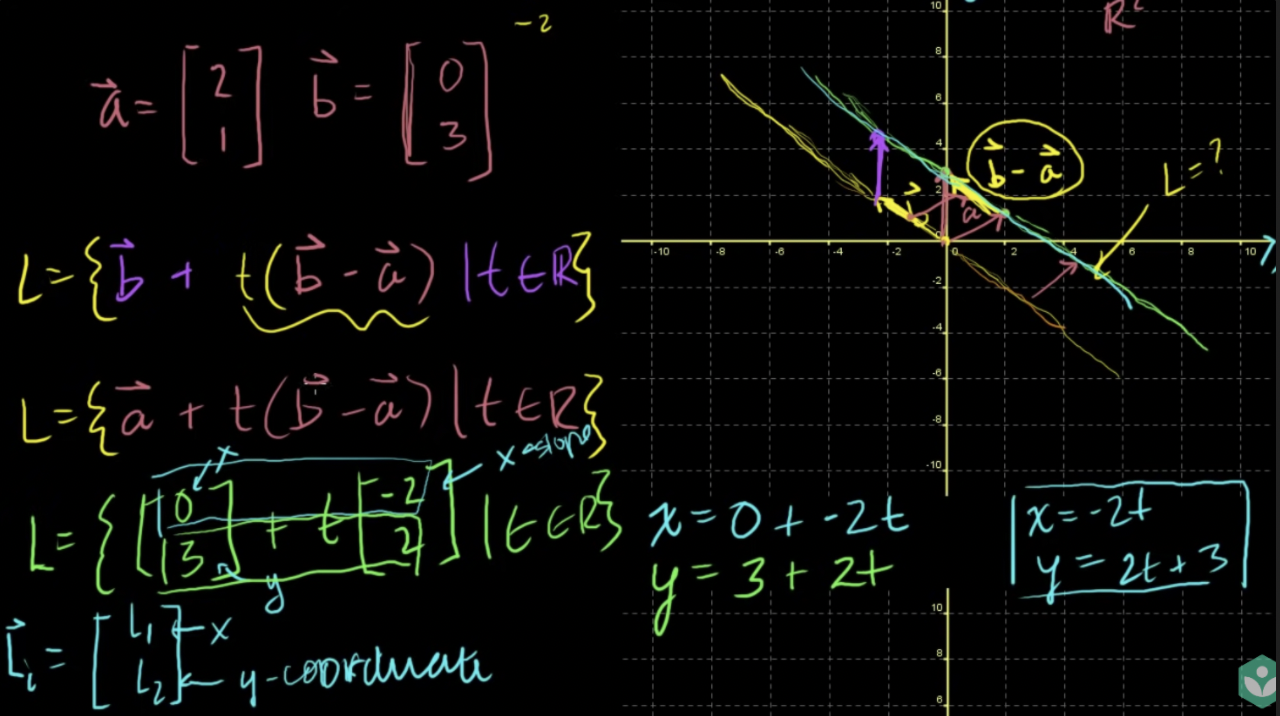
-
벡터의 집합을 매개변수 형식으로 나타내면 ‘x = …’, ‘y = …’형태로 나타낼 수 있음
-
3차원 공간에서 직선 혹은 곡선을 표현하려면 매개변수 방정식을 이용함

- x + y + z = k 는 직선이 아니고 평면임