선형대수학

벡터(vector) 선형대수학을 위한 벡터란? 벡터(vector): 크기(magnitude)와 방향(direction)을 동시에 나타냄 2차원 뿐만 아니라 3, 4, 5, 6차원 이상으로 확장 가능 벡터는 크기와 방향만 신경쓰면됨, 어디서 시작하는지, 어디에 표현

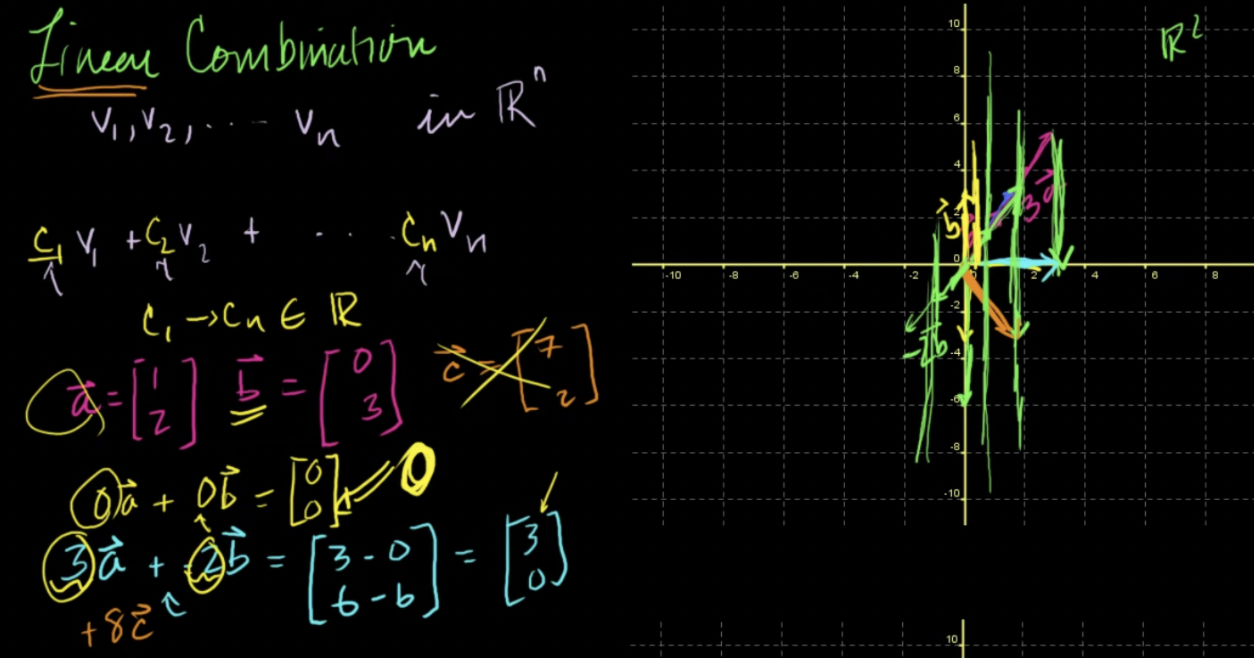
벡터들의 선형결합 각각의 벡터에 임의의 상수배를 한 것을 단순히 다 더하는 것벡터들끼리 곱을 하는 것이 아니라 임의의 상수를 곱한 것을 더하는 것이기에 ‘선형'결합이라고 부름생성: 벡터의 선형결합으로 나타낼 수 있는 모든 벡터벡터a와 벡터 b의 선형결합으로 R2 위의

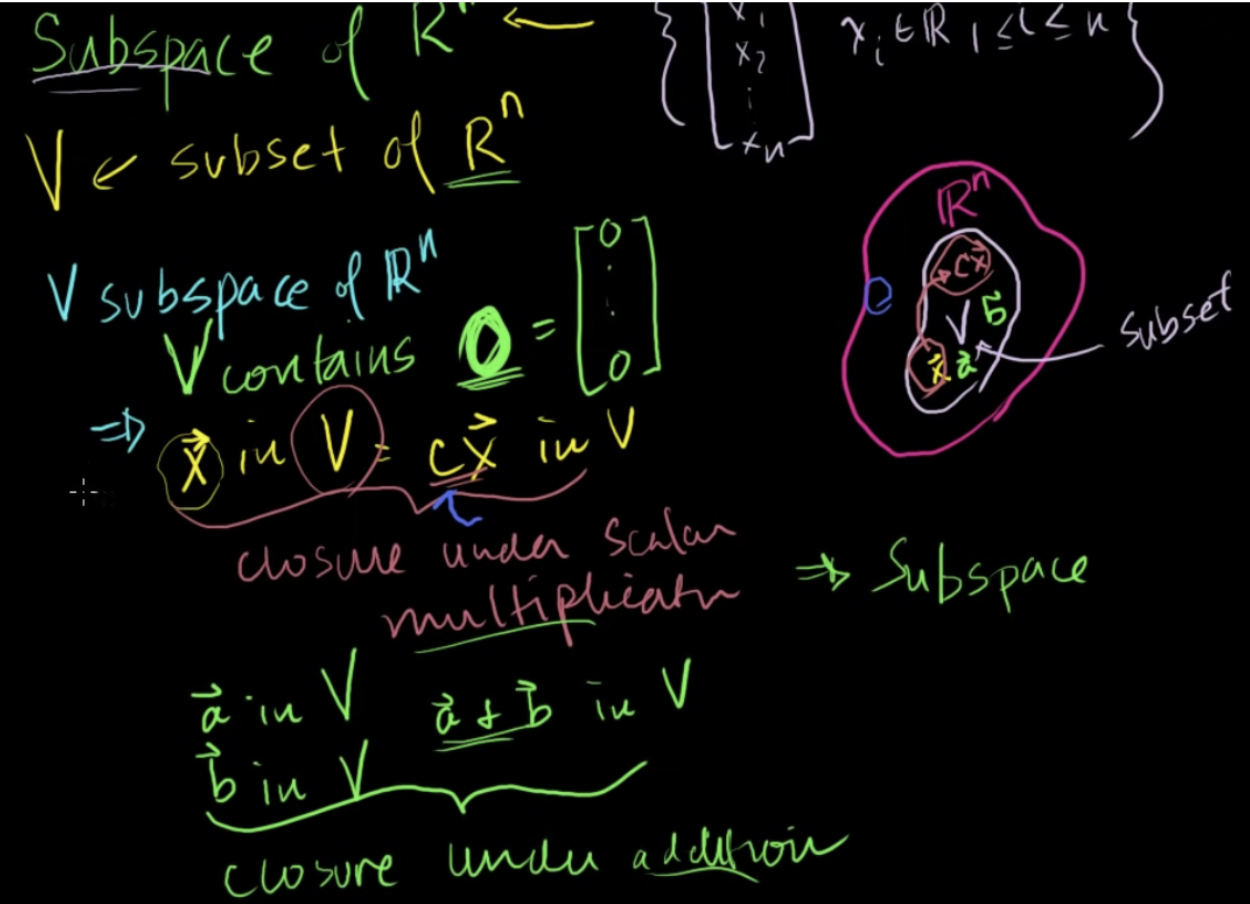
V가 Rn의 선형 부분공간(linear subspace라는 것은 3가지를 의미함V가 영벡터를 포함x가 V에 포함된 벡터라면 x에 임의의 스칼라를 곱한 값(cx)또한 V에 있음 (닫혀있음, closure)만약 집합의 임의의 원소를 가지고있다면 곱셈에 대해 닫혀있는 것스칼

벡터의 곱을 하기 위한 두 가지 방법 중 하나는 내적(Dot Product)내적은 a • b 로 표현함내적은 두 벡터를 곱하여 그 결과 스칼라값을 갖게됨길이(Length)는 || a || 로 표현길이: 각각의 성분을 제곱하고 모두 더한 값의 제곱근과 같음자기 자신과 내

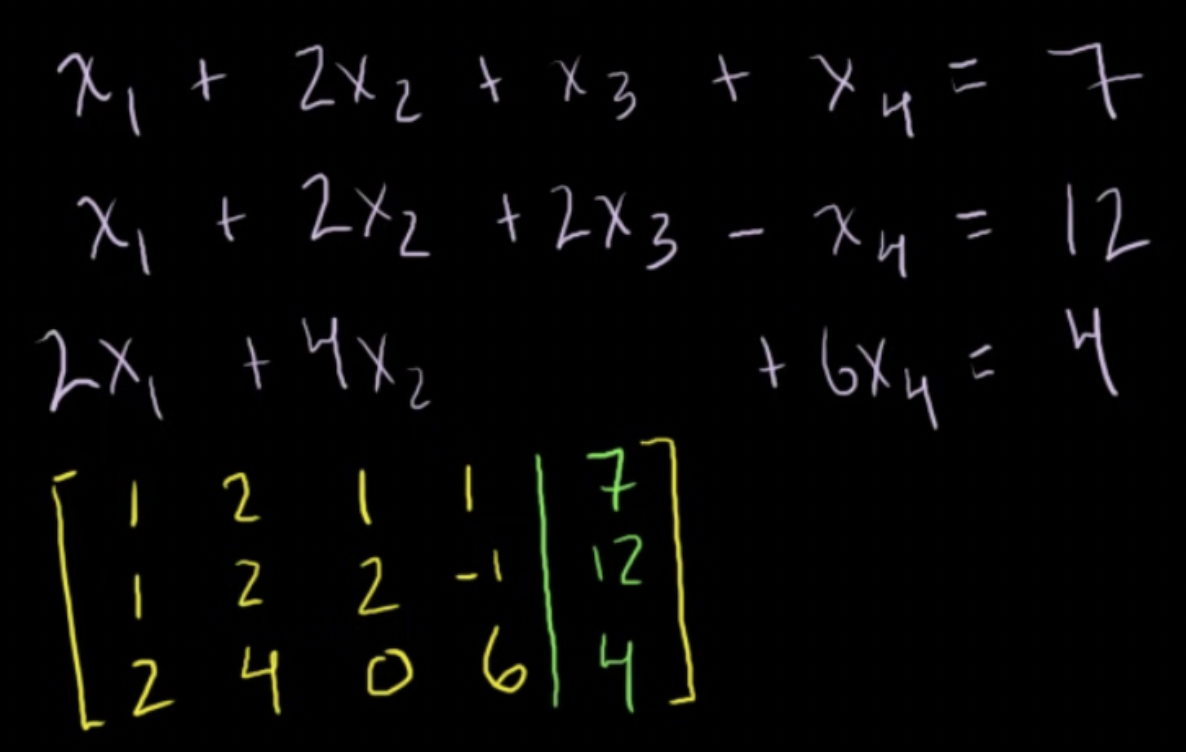
3개의 방정식을 행렬로 나타내고, 어떤 행이든 선형계수가 1이 되고 그에 해당하는 열의 나머지 수들이 0이 되게 함 기약행사다리꼴(Reduced Row Echelon Form) 피벗 성분(Pivot entry): 각 열에서 유일하게 0이 아닌 수zeroed out

행렬과 벡터를 곱할때 행렬에 곱하려는 벡터의 항목이 행렬의 열의 개수만큼 존재할 때만 가능함 행벡터와 열벡터의 곱을 해야할 때, 열벡터의 전치행렬을 활용하는 방법매트릭스 곱하기 벡터는 매트릭스의 행을 곱하려는 벡터와 내적시킨것과 같음매트릭스의 열벡터들의 선형조합으로