선형결합 & 선형종속
선형결합(Linear Combination)과 생성(Span)
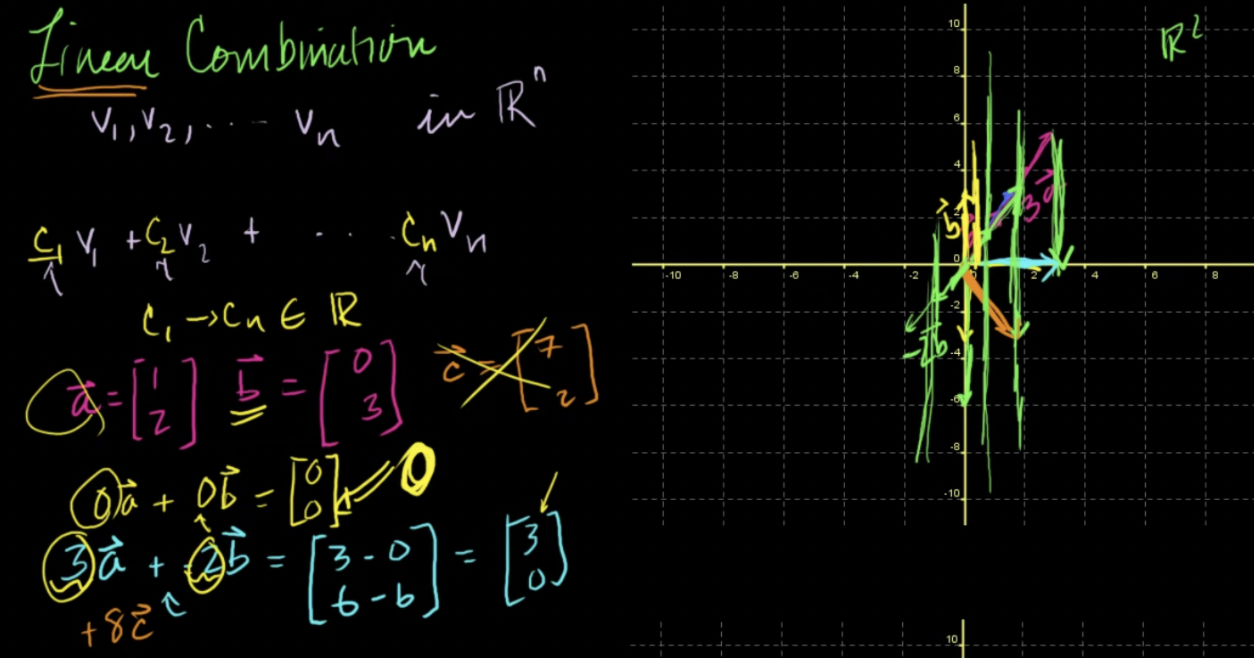
-
벡터들의 선형결합 각각의 벡터에 임의의 상수배를 한 것을 단순히 다 더하는 것
-
벡터들끼리 곱을 하는 것이 아니라 임의의 상수를 곱한 것을 더하는 것이기에 ‘선형'결합이라고 부름
-
생성: 벡터의 선형결합으로 나타낼 수 있는 모든 벡터
-
벡터a와 벡터 b의 선형결합으로 R2 위의 모든 점을 나타낼 수 있음
-
a와 b의 생성(span): R2 혹은 R2 위의 모든 벡터
-
그렇다고 아무 벡터 2개를 선형결합한다고 모든 점을 나타낼 수 잇는 것은 아님
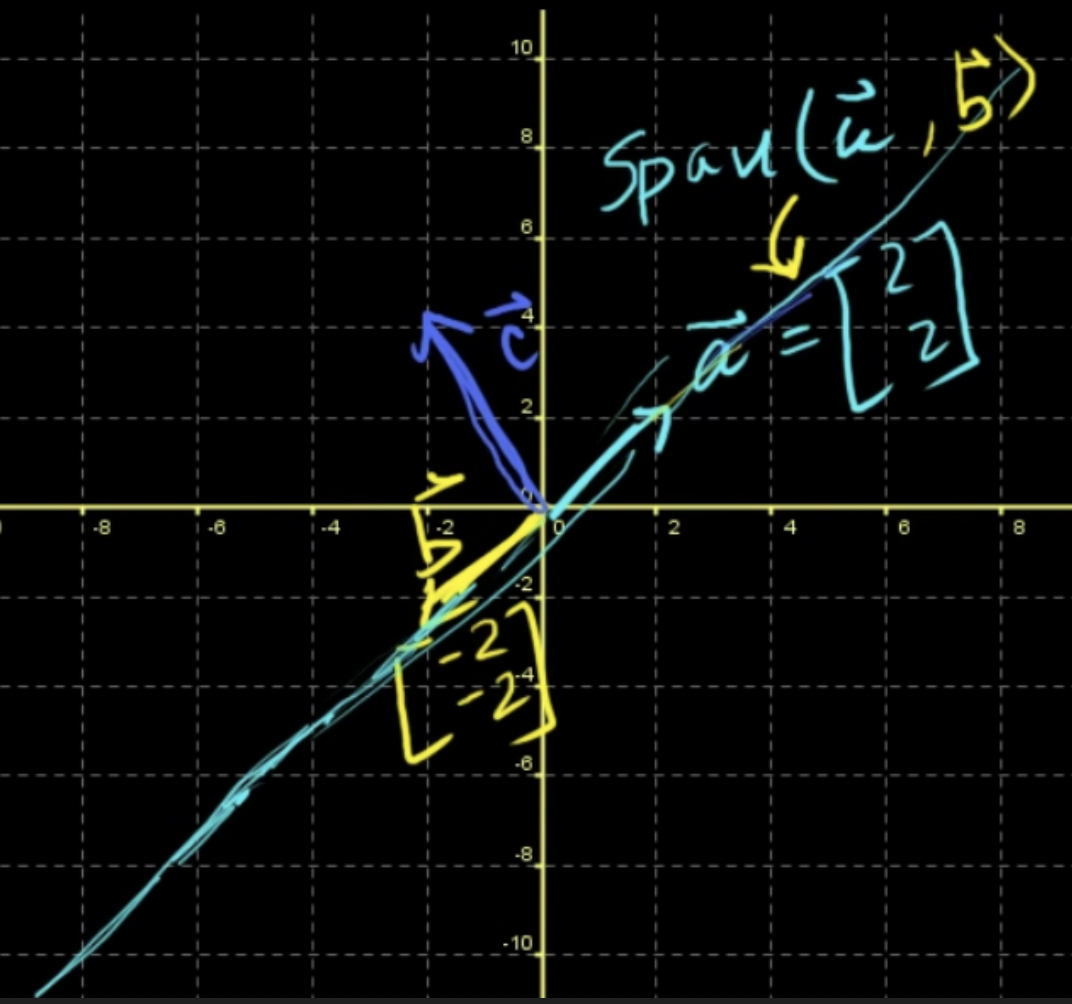
- (2,2)와 (-2,2)를 선형결합하면 어떠한 상수배를 하든 같은 하나의 선 위에 있게 됨
- 두 벡터는 같은 직선상에 있으면 안됨
- 영벡터는 0 이니까 아무리 상수배를 해도 영벡터의 생성(span)은 (0,0)
-
a의 생성: a 자신의 선형결합으로 얻을 수 있는 벡터, a의 크기를 바꾸면서 얻는 직선
-
R2의 어떤 벡터든 단위벡터 i(1,0), j(0,1)로 나타낼 수 있음
-
span(v1,v2,…,vn) = {C1v1+C2v2+…+Cnvn}
- 생성은 이 벡터들의 선형결합으로 나타낼 수 있는 공간 전체를 나타냄
선형독립(Linear Independence)이란?
- 벡터(2,3), 벡터(4,6)과 같은 경우 서로 상수배이므로 두 벡터의 선형결합 대신 한 벡터의 스칼라 겹합으로 줄일 수 있음
- R2의 두 벡터가 동일선상에 있을 때 생성은 직선 하나로 나타냄
→ 선형종속(linearly dependent): 집합의 한 벡터를 집합의 다른 벡터의 선형결합으로 나타낼 수 있는 것
-
R2를 표현하는 두 개의 벡터가 있을 때 R3를 표현하기 위하여 세번째 벡터를 추가할 때 만약 위 두개의 벡터와 동일평면상에 있다면 더이상의 방향성을 추가하지 못하기에 이 세 벡터의 집합은 선형종속이 됨

- R3로 나타내려면 세번째 벡터는 평면을 벗어나야 함
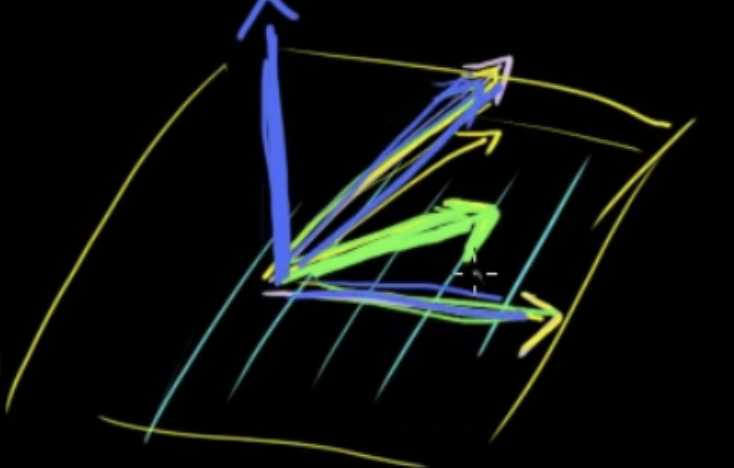
- 두 벡터 생성의 바깥에 있으면 두 벡터의 선형결합으로 나타낼 수 없으므로 선형독립
- R3로 나타내려면 세번째 벡터는 평면을 벗어나야 함
-
벡터가 여분(redundant)이라는 것은 생성에 영향을 미치지 않는다는 뜻, 아래 벡터1과 벡터2의 선형결합으로 만들어지는 벡터3 같은 경우
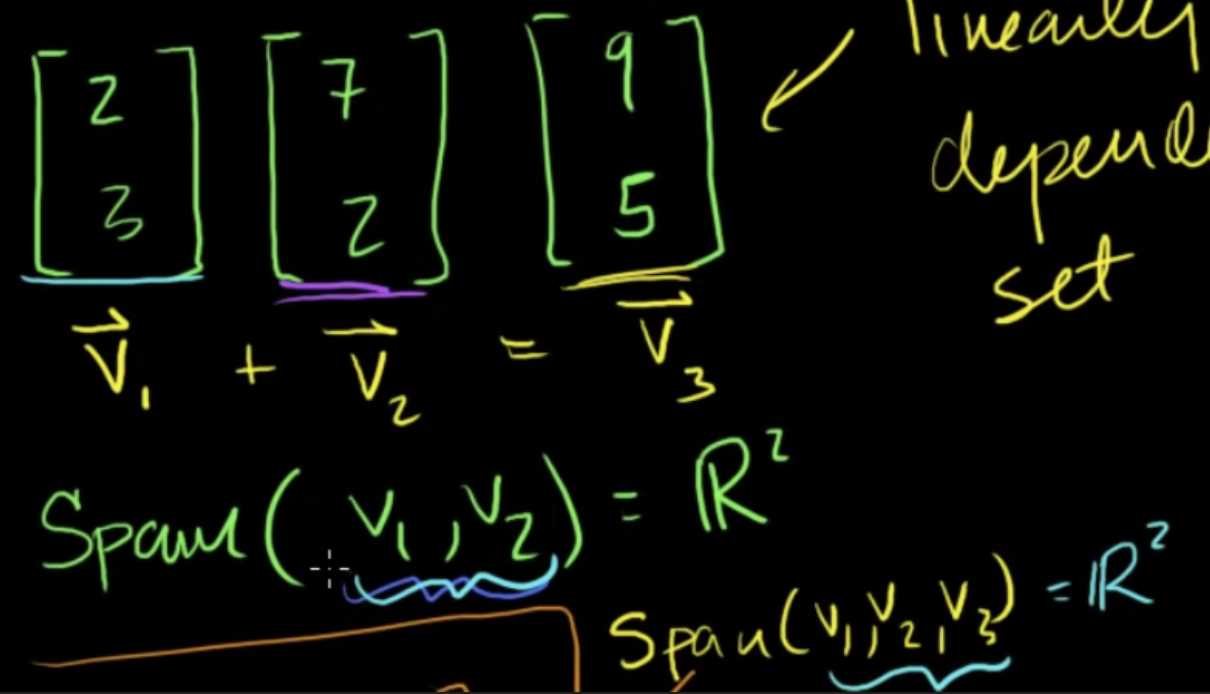
-
서로(벡터)의 선형결합으로 만들어 낼 수 없는 집합의 경우 선형독립(linearly independent)임
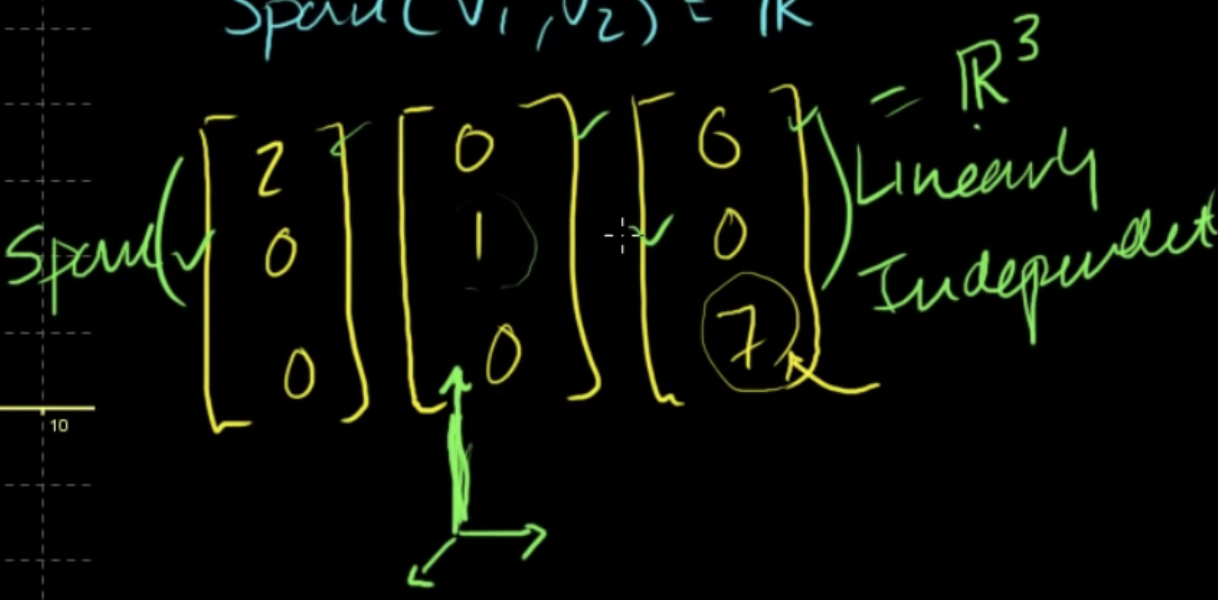
선형독립 더 알아보기
- 필요충분 = iff = if and only if = ↔

- 선형종속인 것은 오른쪽 방정식을 만족하는것과 필요충분조건임
- c가 모두 0이 아닐 때 (적어도 하나는 0 이 아닐 때)
- c가 모두 0이면 선형독립, 이 경우 벡터들의 생성은 R2

- 3개의 벡터로 식을 구할 경우 c하나를 임의로 설정해야 식을 풀 수 있음 (아래는 c가 모두 0이 아니므로 선형종속임을 나타냄)
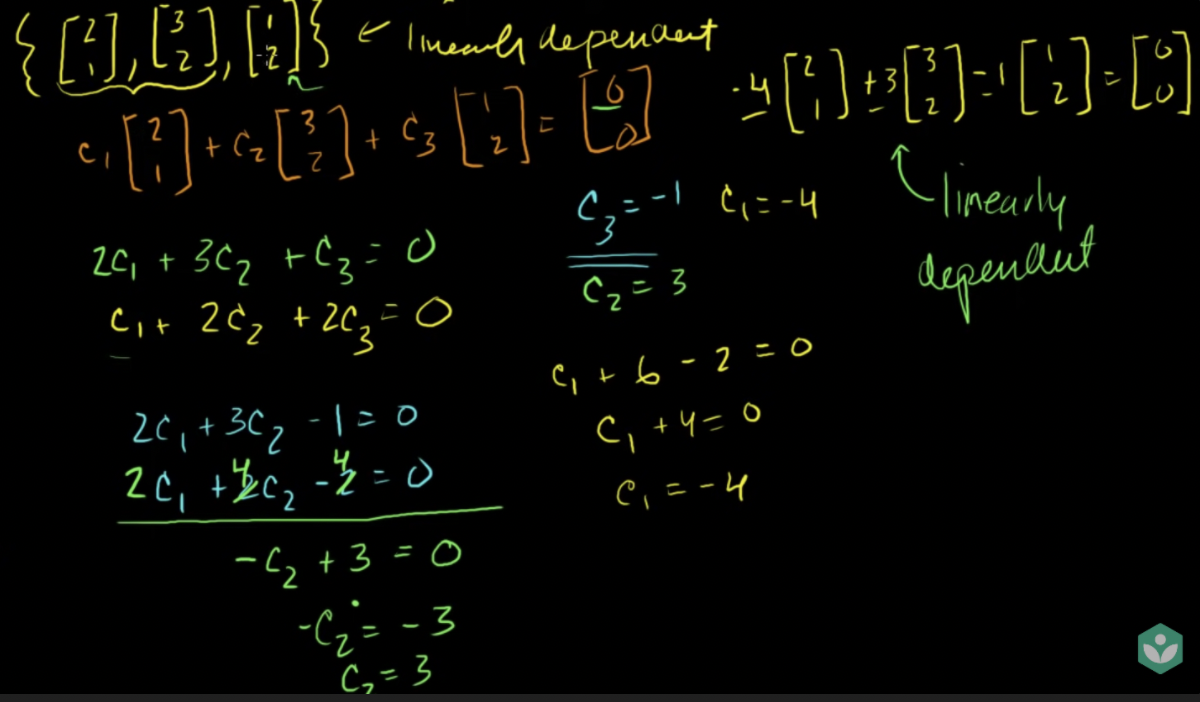
선형생성과 선형독립 예제
- 3차원 벡터이며 3개의 원소드를 가지고 있을 때 이들의 집합 S의 생성은 R3와 같을까?
- 이 벡터들은 모두 선형독립할까?
- 이 두 질문에 대한 답을 구해보자
- R3를 생성한다는 것은 세 벡터로 구성된 임의의 일차식이 R3의 임의의 벡터를 표현할 수 있다는 것
- R3의 임의의 벡터를 실수 a,b,c를 이용하여 표현
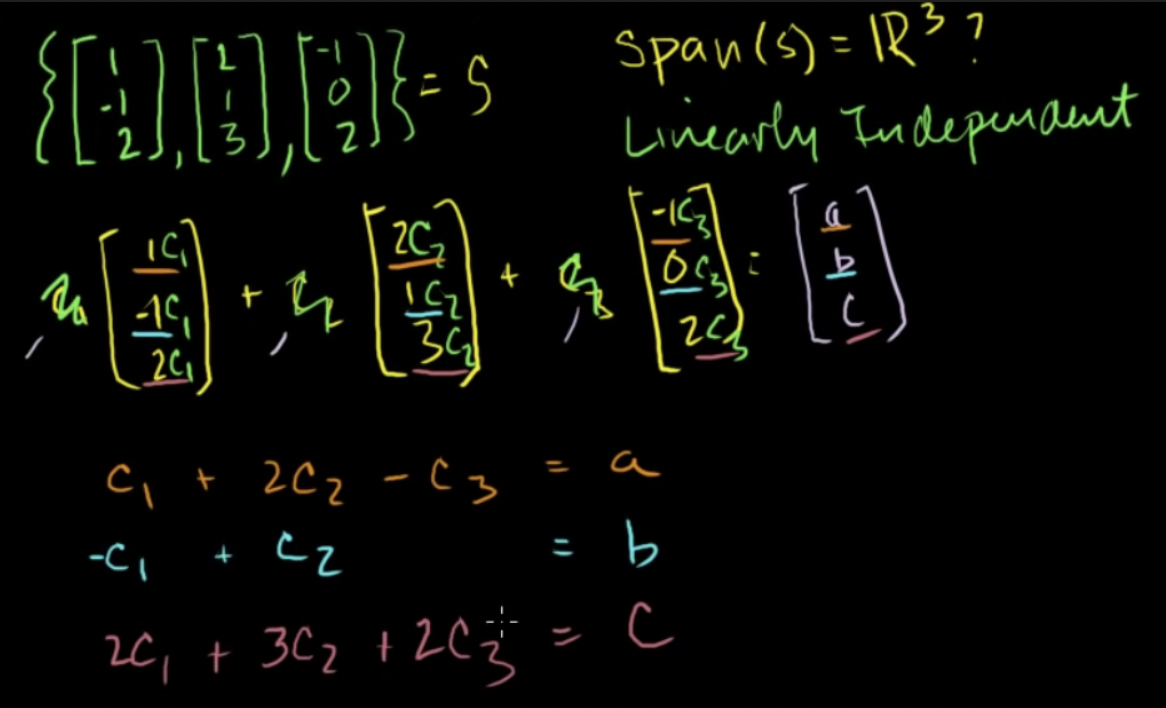
-
a,b,c의 값으로 R3의 임의의 벡터를 고를 수 있으므로 a, b, c = 0이라고 할 때 연립방정식을 통하여 c1, c2, c3 구할 수 있음
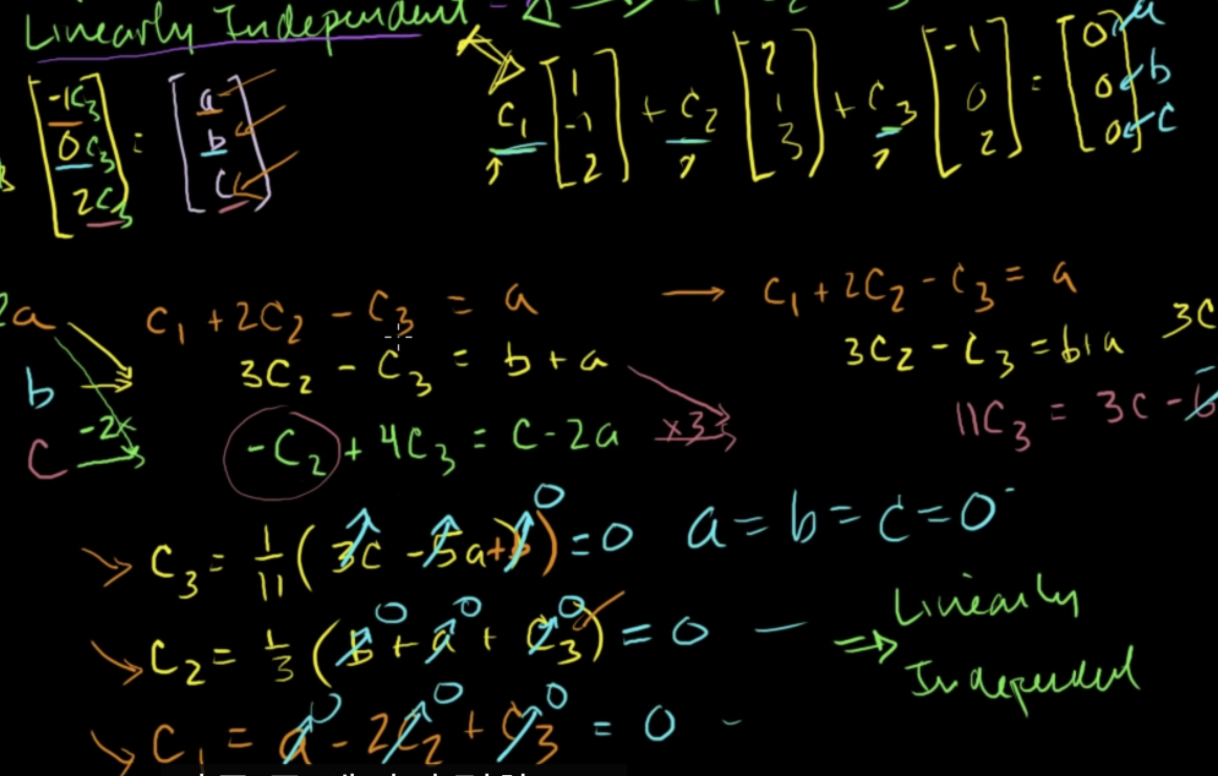
- 위의 경우 이 식의 유일한 해는, 즉 세 벡터 조합이 0의 벡터가 되려면 모든 계수(c1, c2, c3)가 0 이어야 함 → 선형독립, 이 중 어떠한 벡터도 다른 두 벡터의 결합으로 표현될 수 없다는 뜻
- 다른 두 벡터의 조합으로 표현되는 중복되는 벡터가 없다는 것이고, 정확히 세 개의 벡터가 R3를 생성한다는 것
- 그러므로 일반적으로 R3를 생성하는 세 개의 벡터가 있다면 그 벡터들은 선형독립한다는 것
- 세 개의 벡터가 세개의 요소로 된 집합이며 모두 선형 독립한다면 그 벡터들이 R3를 생성한다고 볼 수 있음