영공간과 열공간
행렬 벡터의 곱 (Matrix vector products)
- 행렬과 벡터를 곱할때 행렬에 곱하려는 벡터의 항목이 행렬의 열의 개수만큼 존재할 때만 가능함

-
행벡터와 열벡터의 곱을 해야할 때, 열벡터의 전치행렬을 활용하는 방법
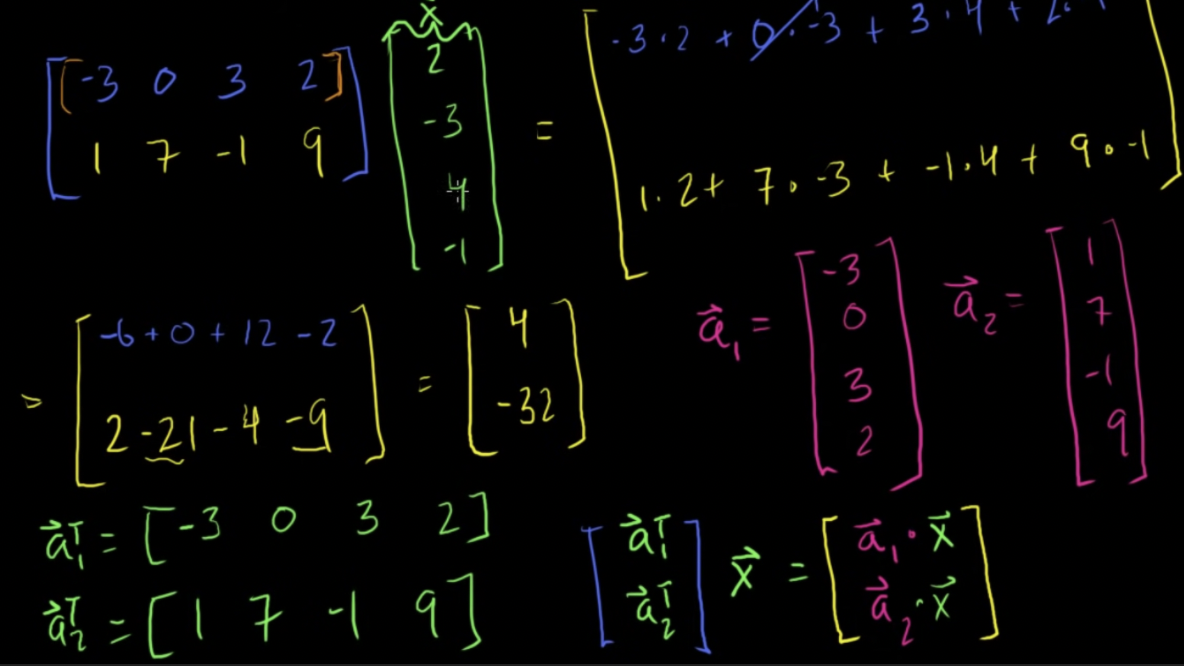
- 매트릭스 곱하기 벡터는 매트릭스의 행을 곱하려는 벡터와 내적시킨것과 같음
-
매트릭스의 열벡터들의 선형조합으로 나타내는 방법 (linear combination of column vectors of matrix)
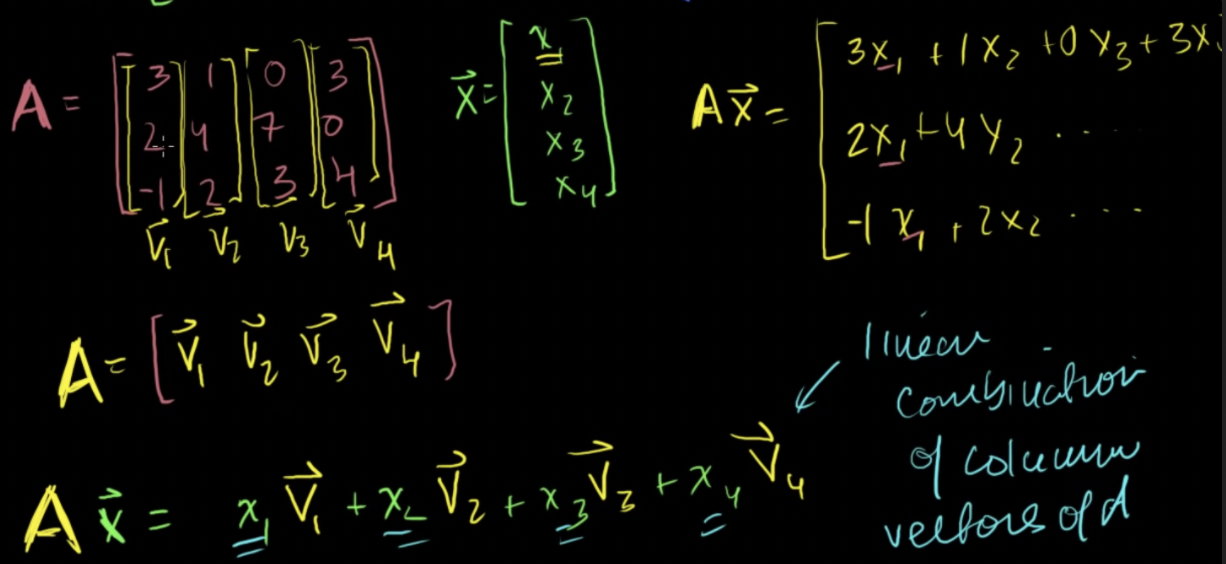
- 매트릭스가 각각의 열에 가중을 정하는 열벡터들의 선형결합
행렬의 영공간이란? (Null Space)
-
부분공간(subspace)의 특징

- 부분공간은 영벡터를 가짐
- 덧셈에 대해 닫혀있음 (v1과 v2가 부분공간의 원소일 때 v1+v2도 부분공간의 원소)
- 곱셈에 대해 닫혀있음 (실수 스칼라 c가 있을 때 c*v1도 부분공간의 원소)
-
영공간(Nullspace)
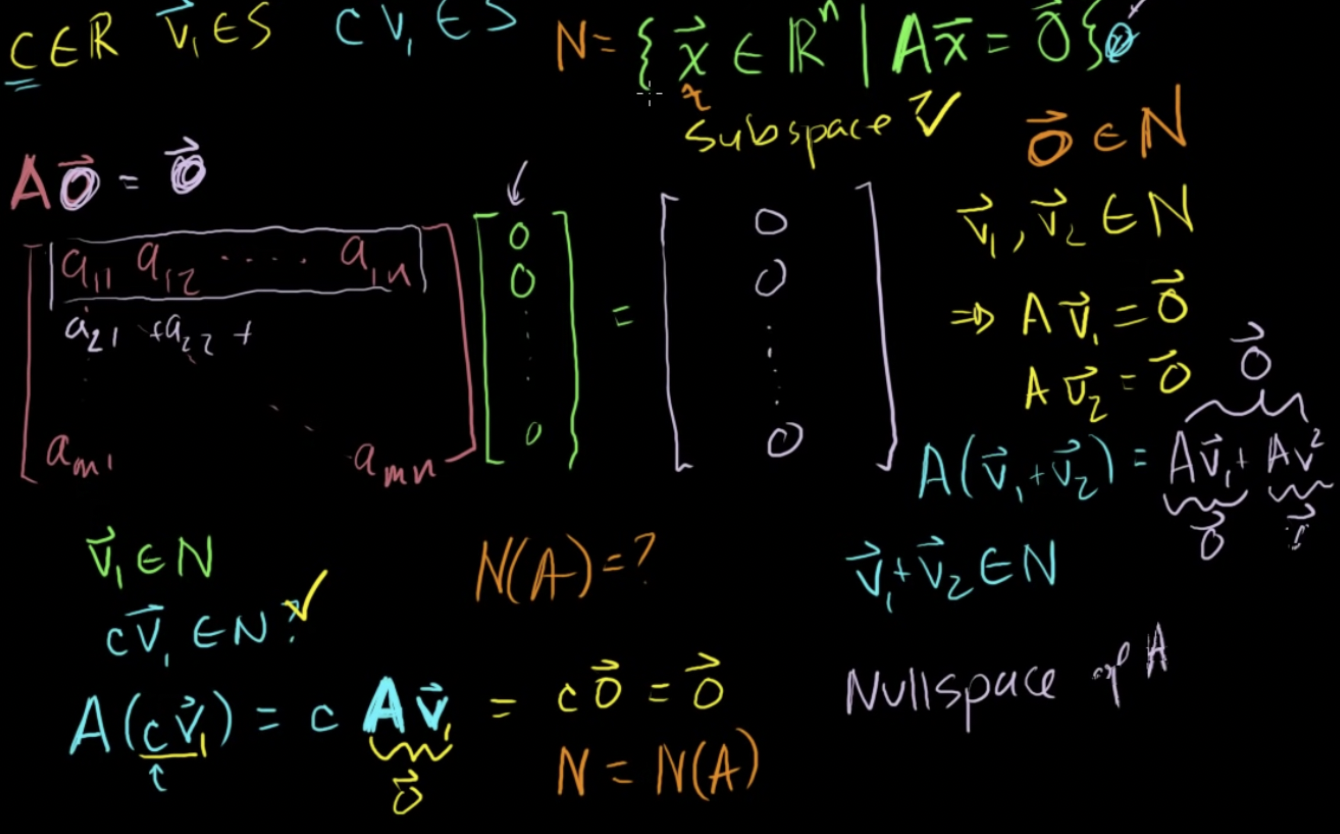
- 영벡터를 포함하고 덧셈, 곱셈에 닫혀있는 n을 a의 영공간이라고 부름
- N = N(A)
- N을 찾으라고 하면 a * x = 0을 만족하는 모든 x의 집합을 찾는 것
영공간 2: 행렬의 영공간 계산하기
-
영공간: 행렬과 곱했을 때 영벡터가 나오는 모든 벡터의 집합
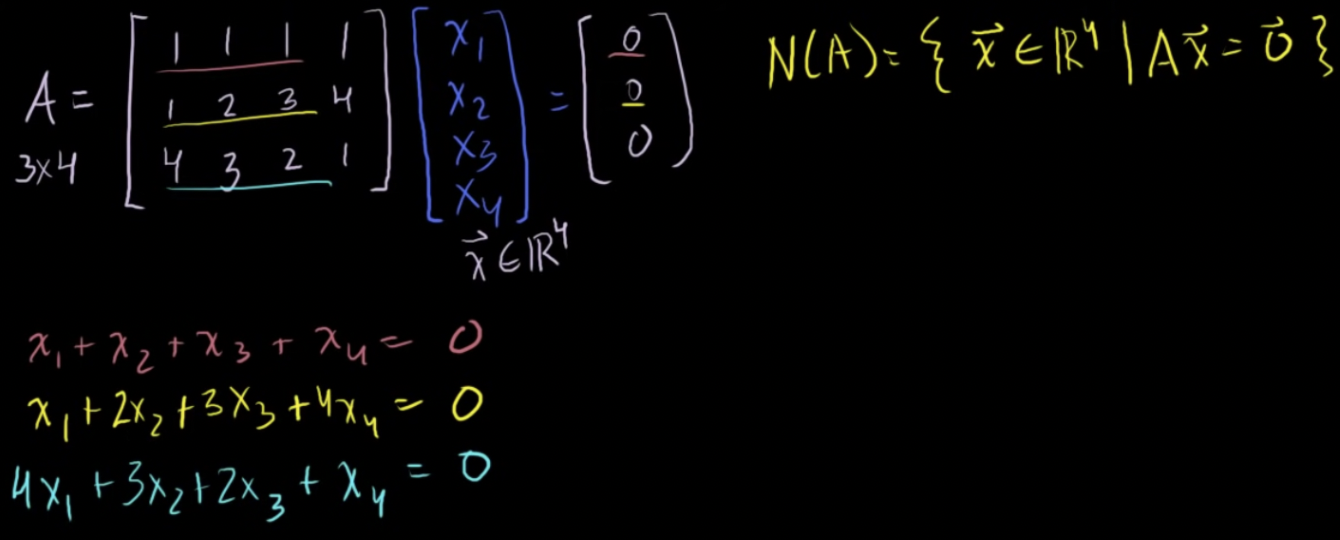
- 세개의 방정식을 첨가행렬꼴로 나타낸 다음 기약사다리행꼴로 바꿔 해를 구하면 그 해가 바로 영공간임
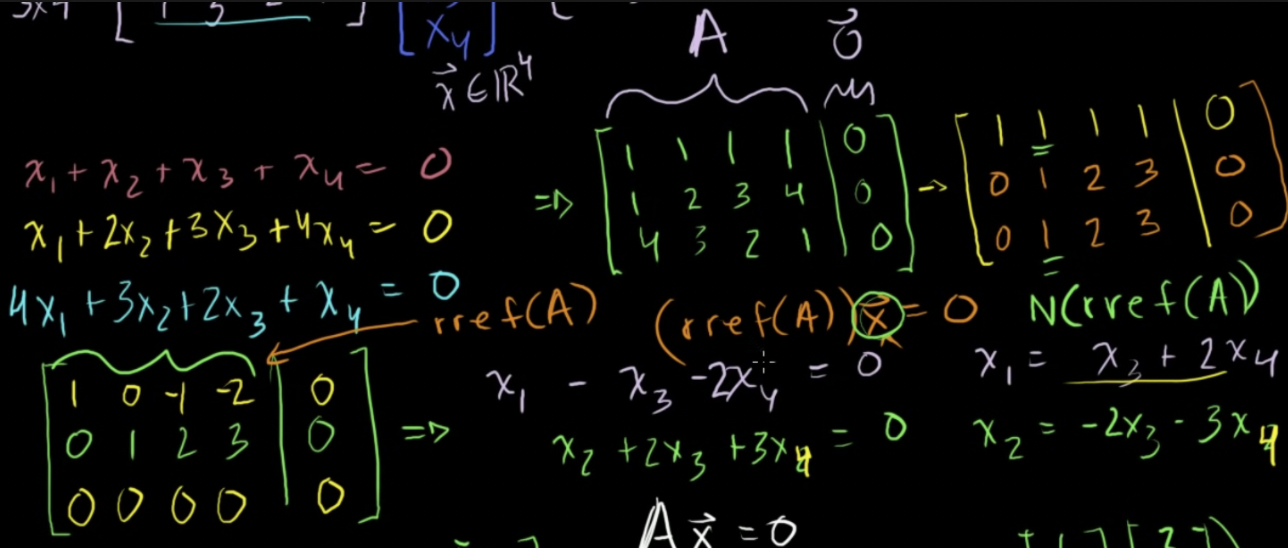
- 영공간은 두 벡터의 일차결합 → span(생성)으로 표현 가능
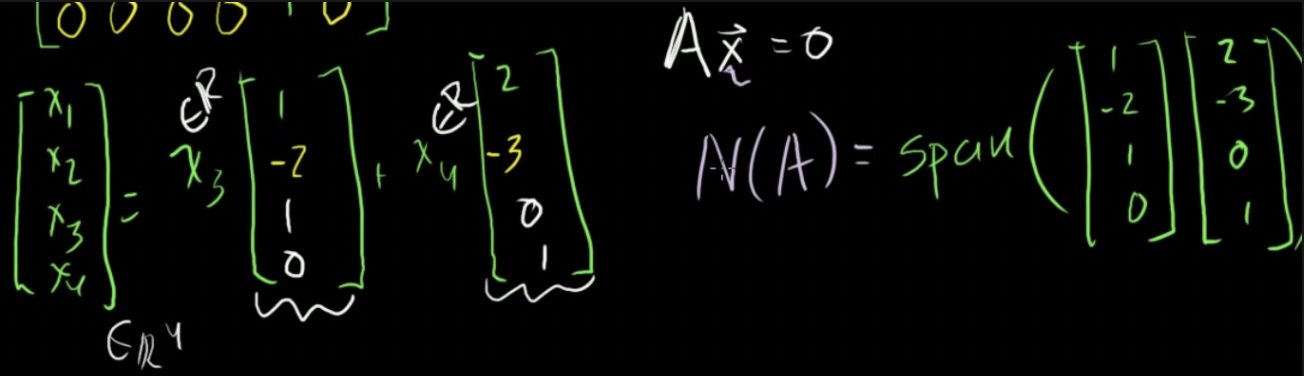
- 세개의 방정식을 첨가행렬꼴로 나타낸 다음 기약사다리행꼴로 바꿔 해를 구하면 그 해가 바로 영공간임
- A의 영공간은 기약사다리행꼴의 영공간과 같음

영공간 3: 선형 독립과의 관계
-
영공간의 정의

- x가 n차원 공간의 원소여야 하는 이유: 매트릭스가 mxn일 때 매트릭스와 벡터의 곱이 가능하려면 벡터는 nx1의 이어야하기 때문에
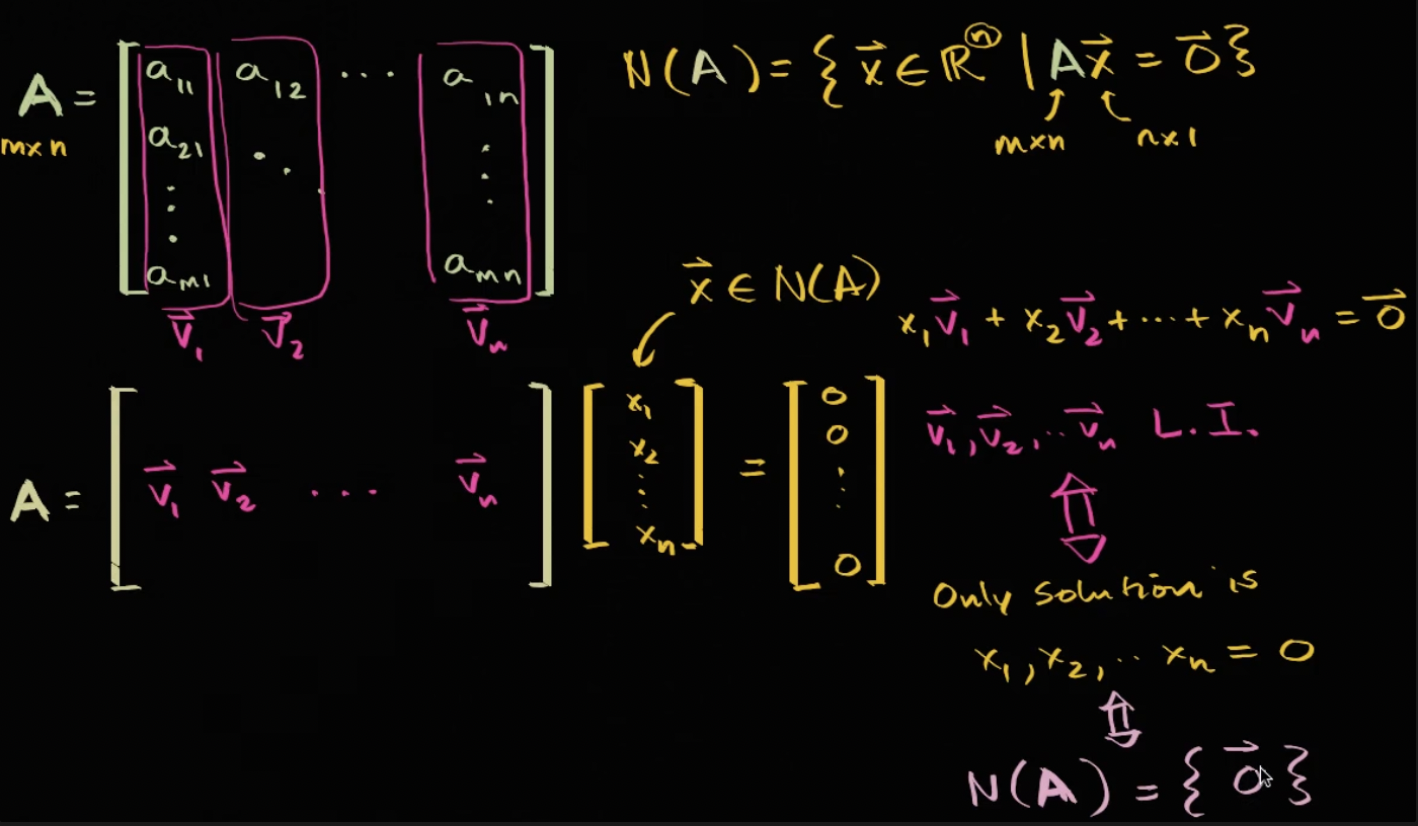
- v1~vn의 벡터들이 선형독립이면 이 식의 유일한 해(벡터에 곱해진 가중)는 x1,~xn이 모두 0인 때
- x1~xn이 모두 0일때 벡터 v1~vn이 모두 선형독립
- 유일한 해가 x1부터 xn까지 0일때 라는 것은 N(A)가 제로벡터 하나만을 포함한다는 것
- 매트릭스의 열벡터가 선형독립한다면 그 매트릭스의 영공간은 제로벡터만 포함함
- 매트릭스의 영공간이 제로벡터를 포함한다면 매트릭스의 열이 선형독립하는 것
행렬의 열공간 (Column Space)
-
열공간은 열벡터의 모든 가능한 선형결합의 공간 (벡터 집합의 생성)
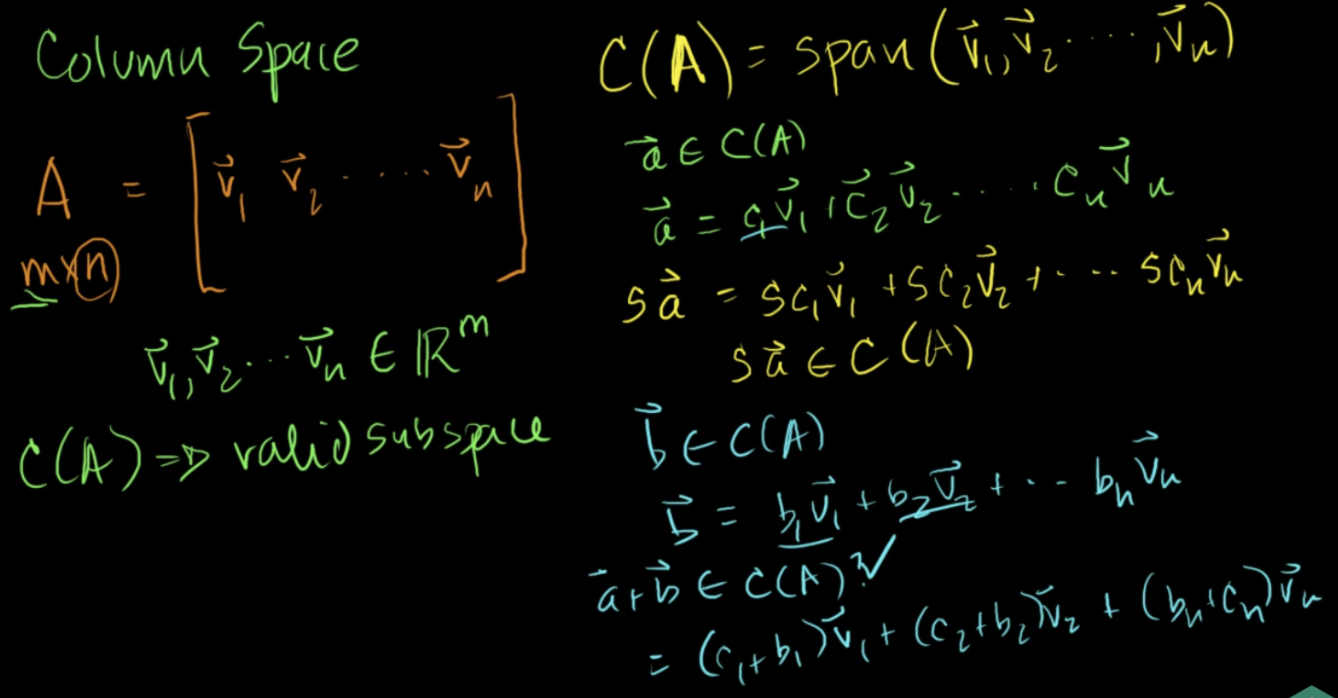
- 열공간 C(A) = span(v1, v2, …, vn)
- 곱셈에 대해 닫혀있음 (sa는 생성의 원소)
- 덧셈에 대해 닫혀있음 (a+b는 생성의 원소)
- 그러므로 열공간은 유효한 부분공간 (valid subspace)
-
열공간: Ax가 가질 수 있는 모든 값

- Ax가 가질 수 없는 어떠한 값과 같다고 가정하면 해가 존재하지 않음
- 해가 존재한다면 b2가 Ax가 가질 수 있는 값 중 하나일 때 Ax=b2를 만족시키는 x를 구할 수 있음
영공간과 열공간의 기저
-
열공간 구하기: 행렬A의 벡터의 span과 같음
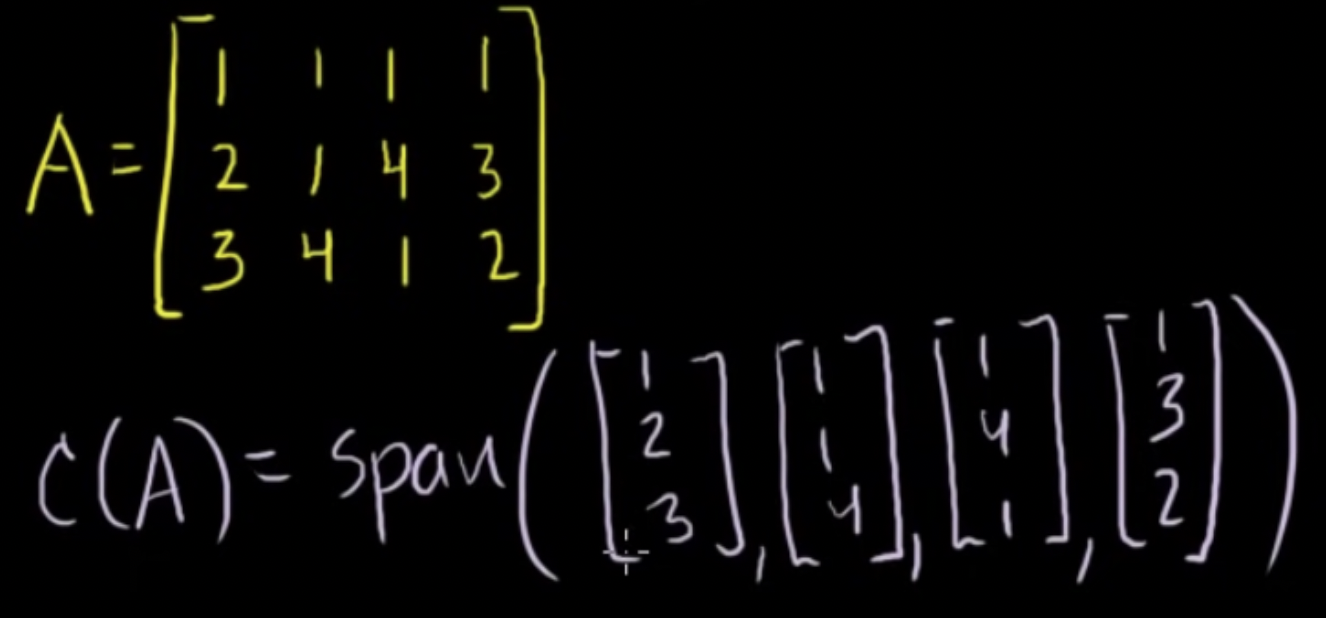
- 만약 벡터들이 선형 독립성을 가진다면 이 벡터들이 열공간 A의 기반이 됨
- 선형독립성의 존재여부는 행렬A의 영공간을 구하여 판별 가능하므로 영공간을 구해봄
- 행렬A의 영공간이 0벡터를 가진다면 선형독립성을 가짐
- 행렬A의 영공간은 각 열의 영공간과 같음(기약행사다리꼴의 형태)
- N(A) = N(rref(A))
-
영공간 구하기
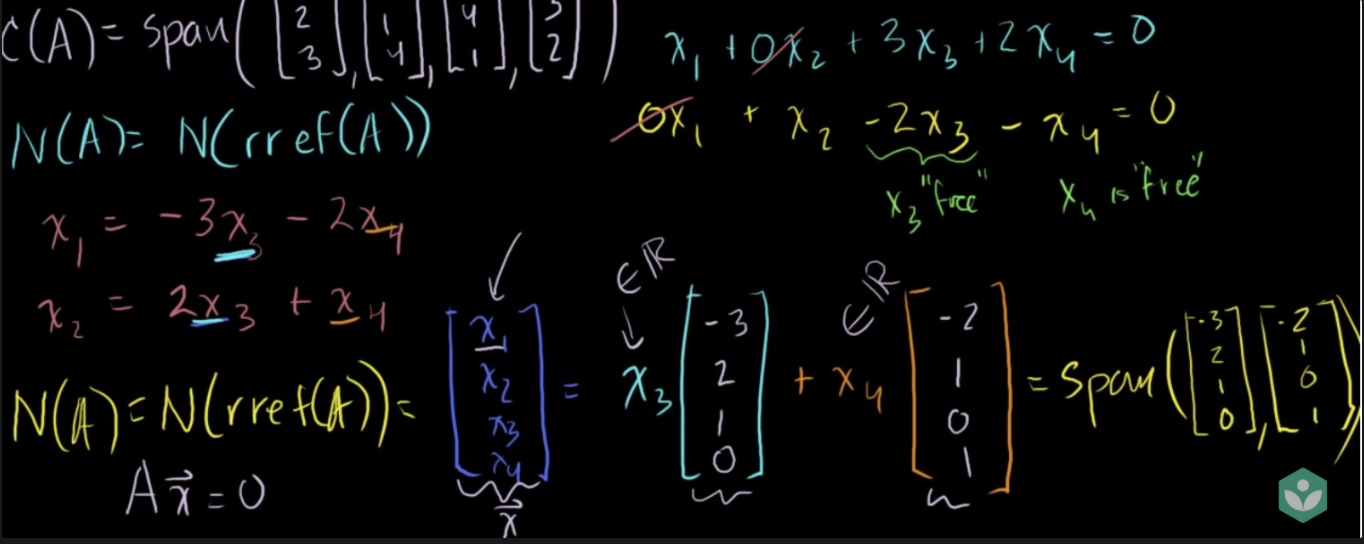
- 영공간은 두 벡터의 span값과 같음
-
선형 독립(Linearly independent)
- 답이 하나, Ax가 0이고 x가 0벡터인 것
- 행렬 A의 영공간은 0벡터인 것
- 영공간이 다른 벡터를 포함하면 선형 독립성을 갖지 않는 것
-
행렬 A의 영공간은 두 벡터의 모든 일차결합벡터를 포함하므로 0을 포함하여 무한한 개수의 벡터들을 포함함
- 하나 이상의 솔루션을 가지기에 일차독립성을 지님 (Linearly dependent set)
- 선형독립적이지 않으르모 열벡터들이 A의 열공간의 기저(부분공간을 생성하는 벡터집합)가 아님
-
기저를 찾기 위해선서 우선 중복벡터를 없애야 함(서로 다른 벡터로 한 벡터를 표현할 수 있다면 없애야 함)
-
자유변수와 피봇변수로 솔루션 풀기
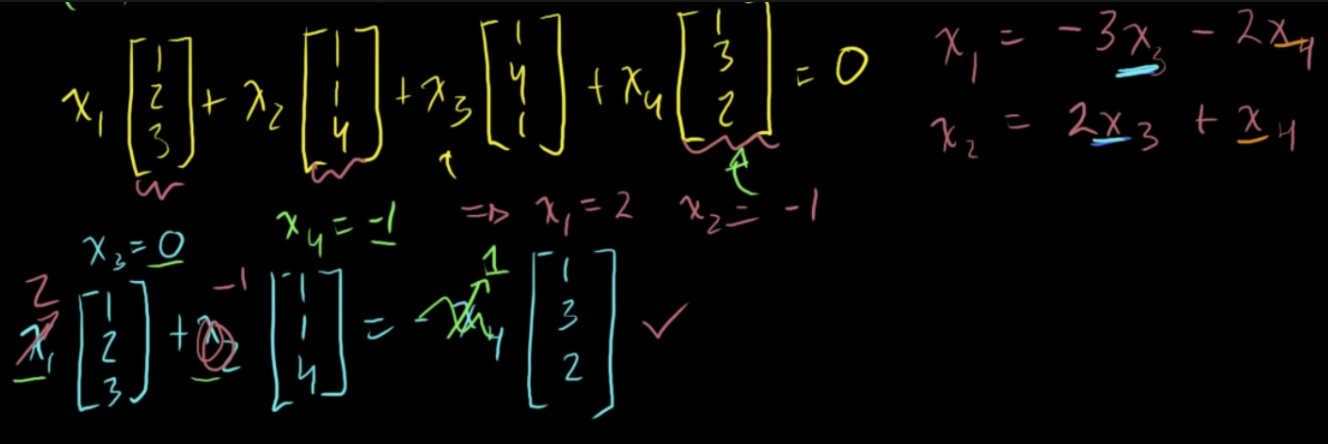
- 네번째 벡터를 첫번째, 두번째 벡터로 표현
- 네번째 벡터는 필요가 없음 → 첫번째와 두번째 벡터의 조합으로도 표현이 가능
- 세번째 벡터도 마찬가지

-
A의 열공간 C(A) = span(v1,v2)

-
v1과 v2가 A의 행 생성을 위한 기반(basis) → 벡터들이 선형독립성을 이룸
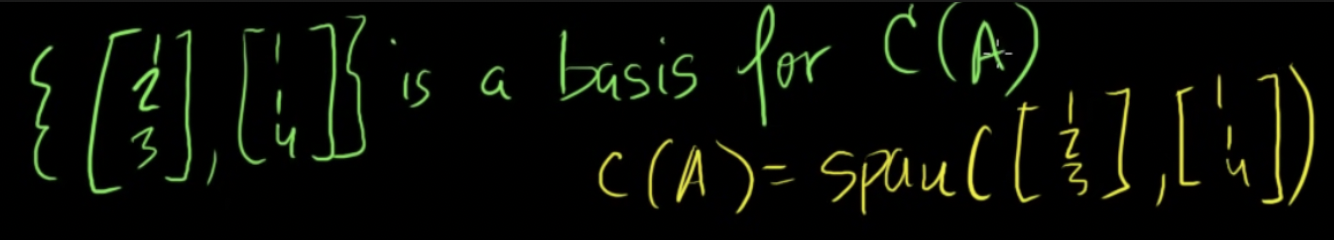
R3에 있는 열공간을 평면으로 시각화하기
-
위에서 본 A의 열공간 시각화하기
-
생성은 R3안에 어떠한 평면을 이룸
-
열 생성의 기반을 찾고, 두 기반벡터의 외적을 이용해 법선벡터를 찾은 후 법선벡터와 평면에서 기반 벡터 하나를 뺀 벡터와의 내적을 이용해 구하기
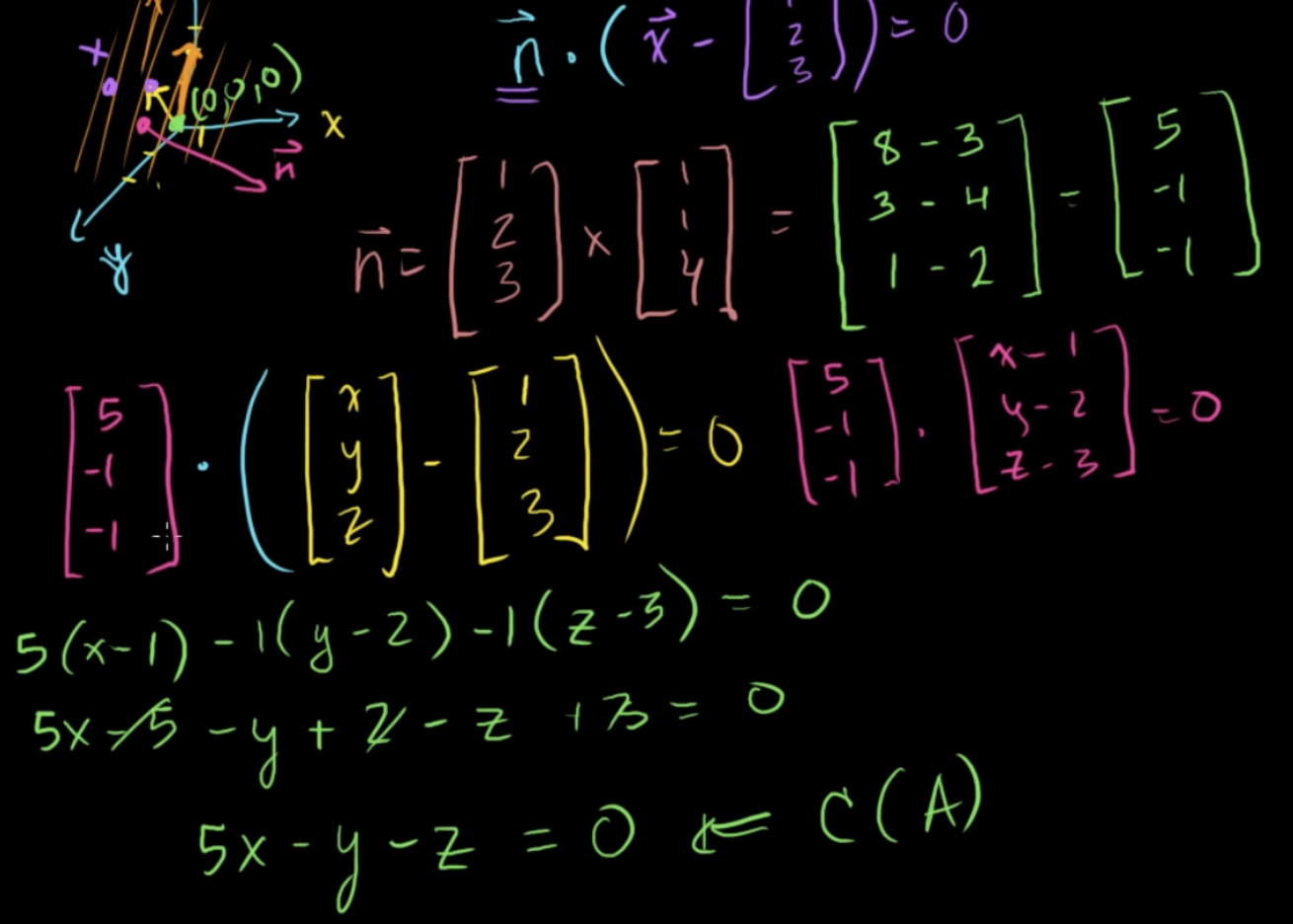
- 법선벡터와의 내적을 이용해 평면의 방정식을 구함
- 법선벡터: R3안의 어떠한 두 벡터의 외적
-
다른 방법으로 찾기 (열 생성의 다른 정의 이용)
- x가 Rn의 성분인 Ax의 유효한 모든 솔루션이라는 것
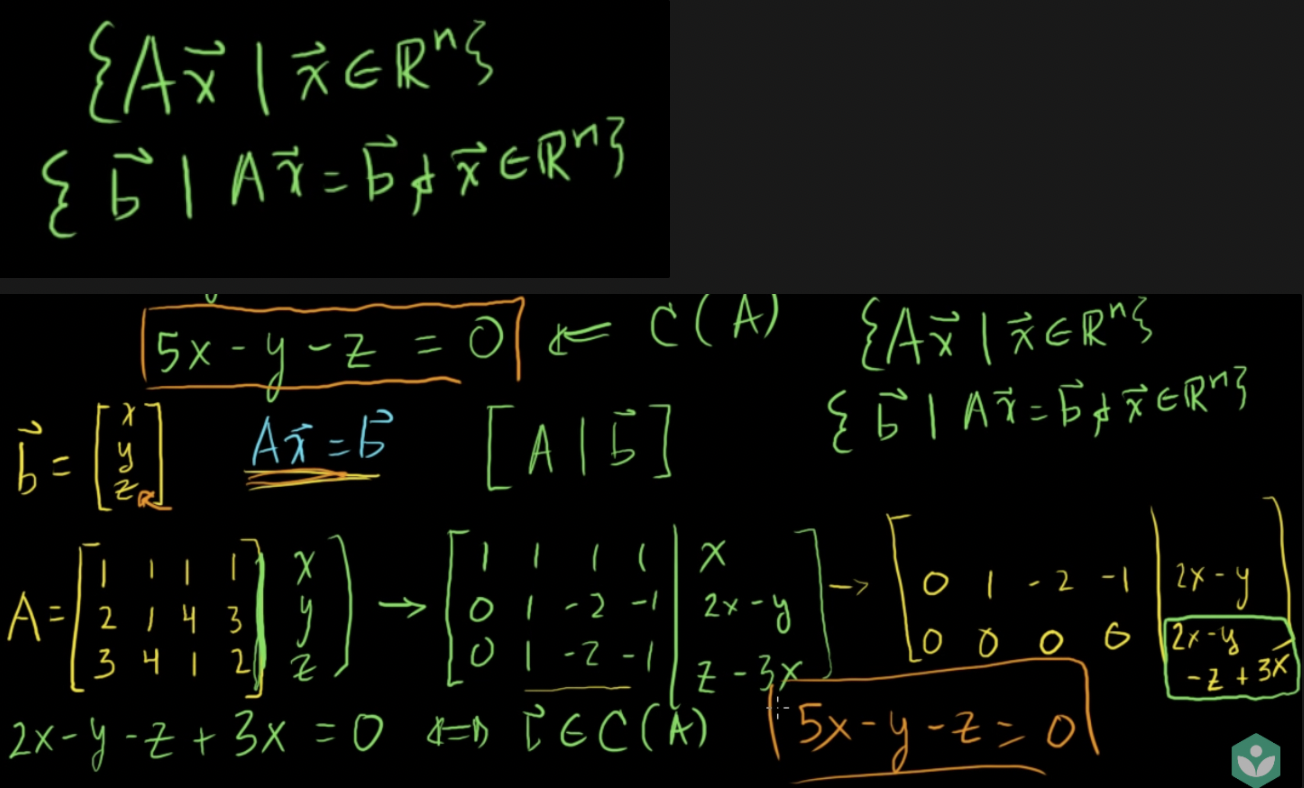
- x가 Rn의 성분인 Ax의 유효한 모든 솔루션이라는 것
증명 : 어떠한 부분간의 기저도 원소의 수가 같습니다.
-
집합 A에 n개의 원소가 있을 때 V를 생성하는 어떠한 집합이던지 최소 n개의 원소를 가짐

-
n보다 적은 원소가 있을때 어떤 모순이 생기는지 살펴보기

-
벡터공간의 어떤 기반 벡터, V의 부분집합의 기반벡터는 모두 같은 원소 개수를 가짐
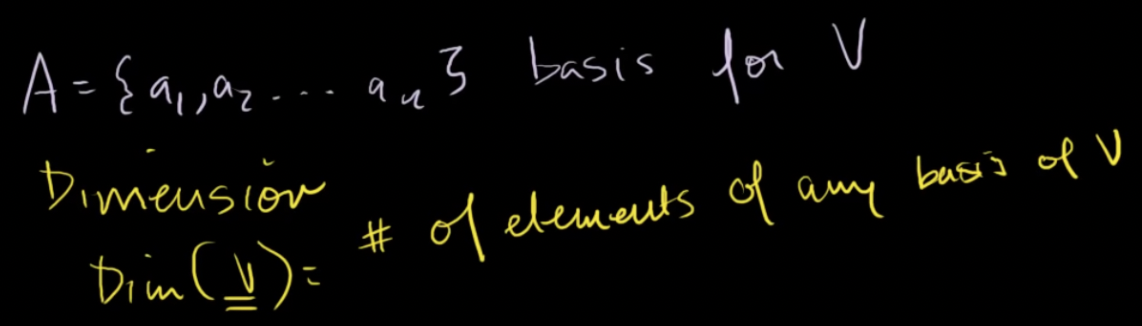
- Dimesnison of V (V의 차원): 원소의 개수
- V의 기반들 모두 같은 개수의 원소를 가짐
-
영공간의 차원
-
영공간 구하기
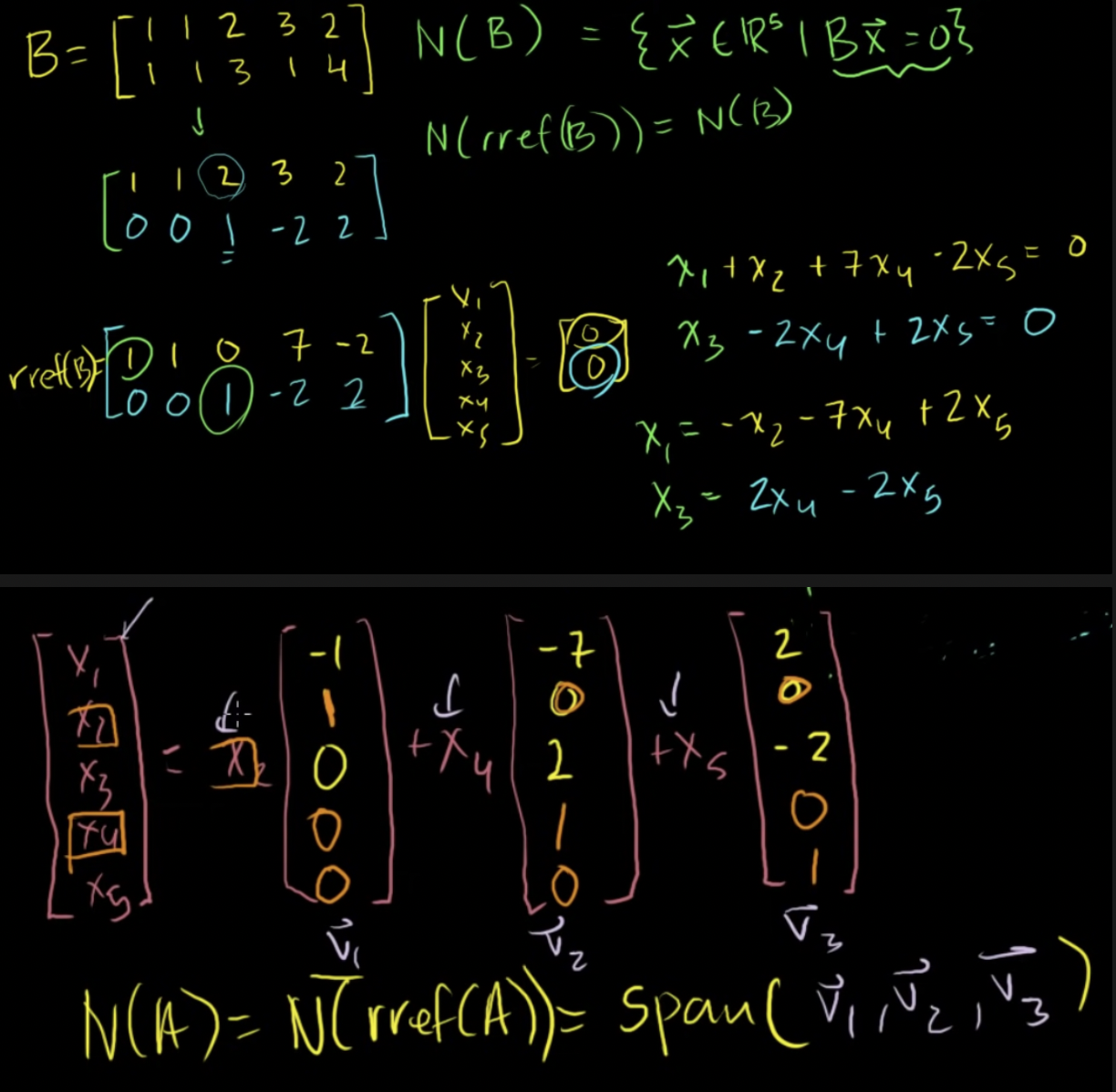
- 벡터들이 선형독립인가? → 선형독립이라면 이 벡터들이 영공간의 기반을 이룸
- 어떠한 벡터도 다른 벡터들의 선형결합식으로 표현할 수 없기에 선형독립임
- v1,v2,v3는 B의 영공간의 기반(basis)
- 차원(Dimension of a subsapce): 부분집합에 대한 기반에 있는 요소들의 개수 (number of elements in a basis for the subspace)
- 어떤 부분집합의 기반들은 모두 같은 개수의 요소를 지님
- B의 영공간의 차원은 → B의 기반 집합안에 존재하는 벡터의 개수, 3차원
- 다른말로 B의 무효성(nullity)라고 함
- 무효성: 3
- 어떤 행렬의 무효성(nullity)은 자유변수의 열 개수, 기약행사다리꼴의 피봇 열이 나닌 것의 개수와 같음 (number of free variables, non-pivot columns in rref(A))
- 자유변수는 다른 벡터들의 선형결합식으로 나타낼 수 없는 벡터들의 개수이기 때문
- 행렬의 무효성은 그 행렬의 기약행사다리꼴 안에 존재하는 피봇 열이 아닌 열의 개수와 같음
- 벡터들이 선형독립인가? → 선형독립이라면 이 벡터들이 영공간의 기반을 이룸
열공간의 차원
-
행렬 A의 열공간은 A의 열벡터들의 선형결합식과 같음 (열벡터들의 생성)

-
열공간의 기반(basis) 구하기 → 기햑행사다리꼴을 구하고 어떤 열이 피봇 열인지 찾음, 그 열들이 기반을 만듦, 랭크를 구하려면 그 열의 개수(피봇 열의 개수)를 셈
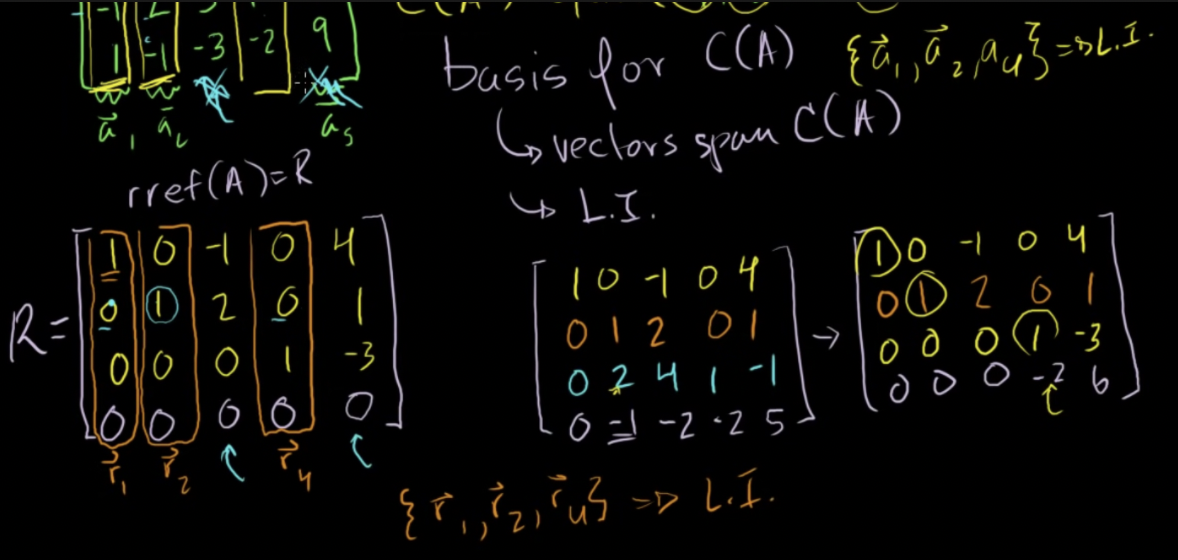
- 피봇이 아닌 열들은 피봇 열들의 선형 결합으로 나타낼 수 있음
- 피봇열들은 서로 선형독립
- a1, a2, a4는 A의 열공간의 기반을 이룸
- 나머지 두개는 이 벡터들의 선형결합식으로 표현이 가능하고 그들은 선형독립성을 지니기 때문
-
A의 열공간의 차원: 열공간의 기반 안에 있는 벡터의 개수, 모든 기반은 같은 개수의 벡터를 가짐
-
Dimension(C(A)) = 3 → (a1, a2, a4)
-
열공간의 차원은 랭크(rank)라고 함
- 모든 열공간을 생성하는 선형독립인 열 벡터들의 개수, 다른 벡터들을 나타낼 수 있는 선형독립적인 열 벡터들의 개수
-
rank(A) = 3
기저 열과 축열과의 관계
-
어떠한 기약행사다리꼴 행렬의 추축열(pivot column)의 집합도 선형독립임
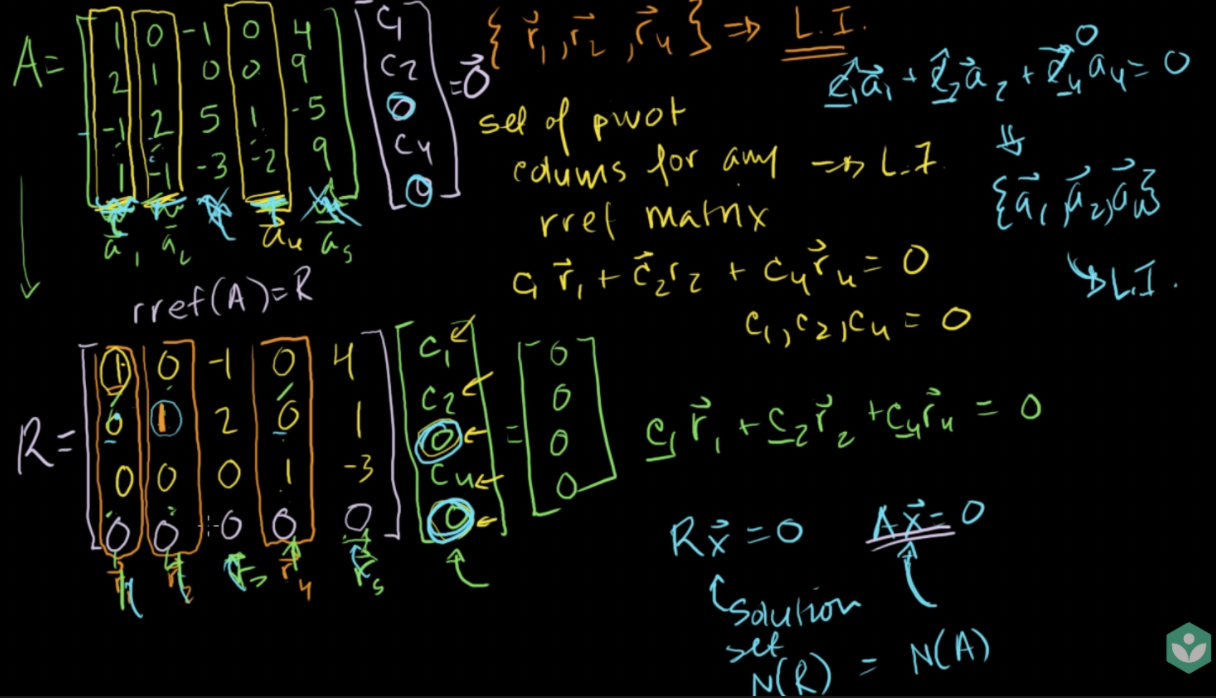
- 각 열의 1은 유일한 위치에 존재하기 때문, 다른 열은 그 자리에 0이 있을 것
- c1r1 + c2r2 + c4r4 = 0은 해가 한 개임
- c1, c2, c4 = 0
- 해집합은 영공간
후보 기저의 A의 열공간 생성
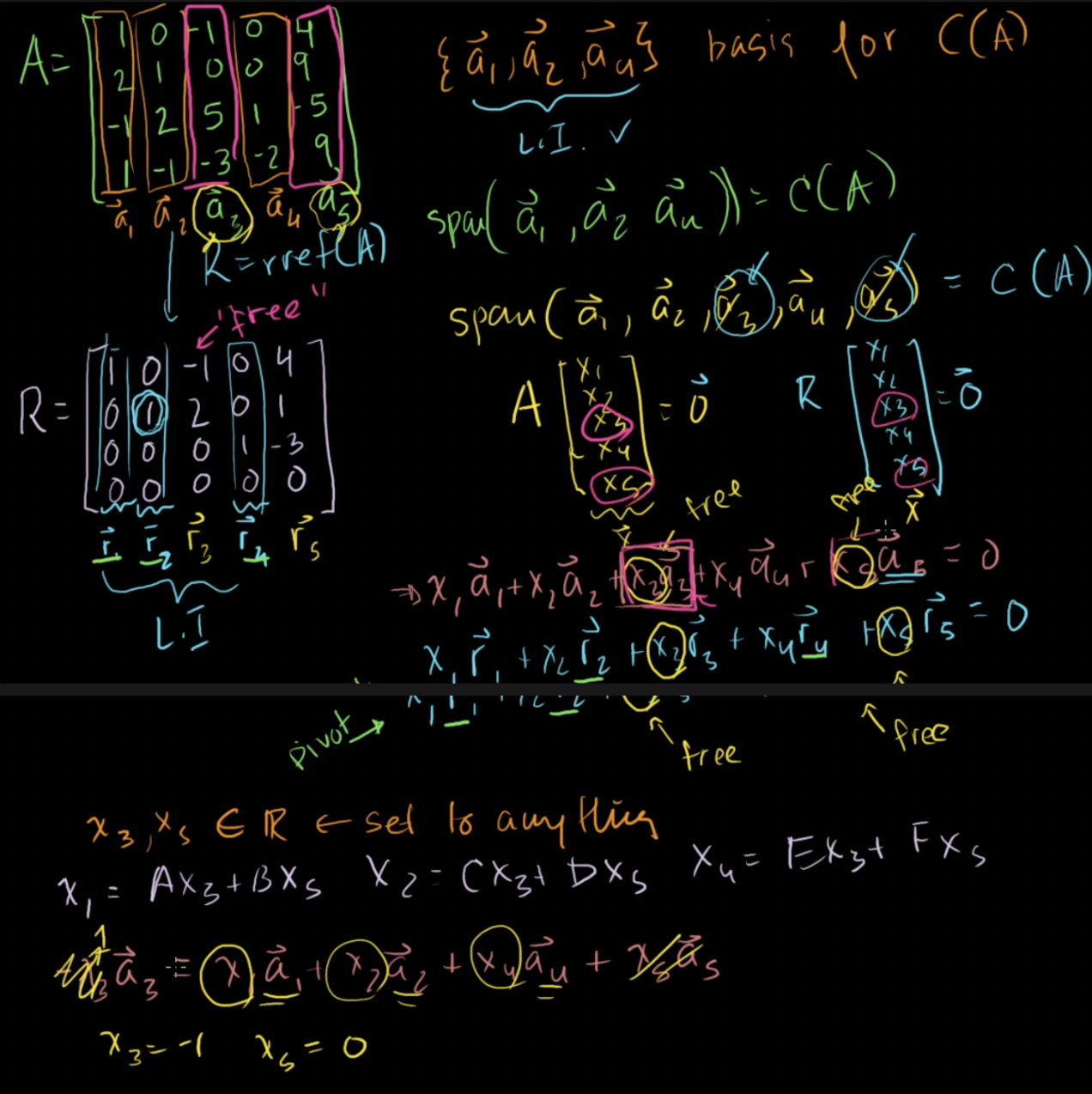
- 자유벡터들은 다른 벡터들의 선형결합으로 나타낼 수 있음
- 피봇 열들의 열벡터들이 열공간의 기반을 나타냄