연립방정식을 풀기위한 행렬
행 사다리꼴 행렬을 이용하여 3차 연립방정식과 4개의 변수 풀기
-
3개의 방정식을 행렬로 나타내고, 어떤 행이든 선형계수가 1이 되고 그에 해당하는 열의 나머지 수들이 0이 되게 함
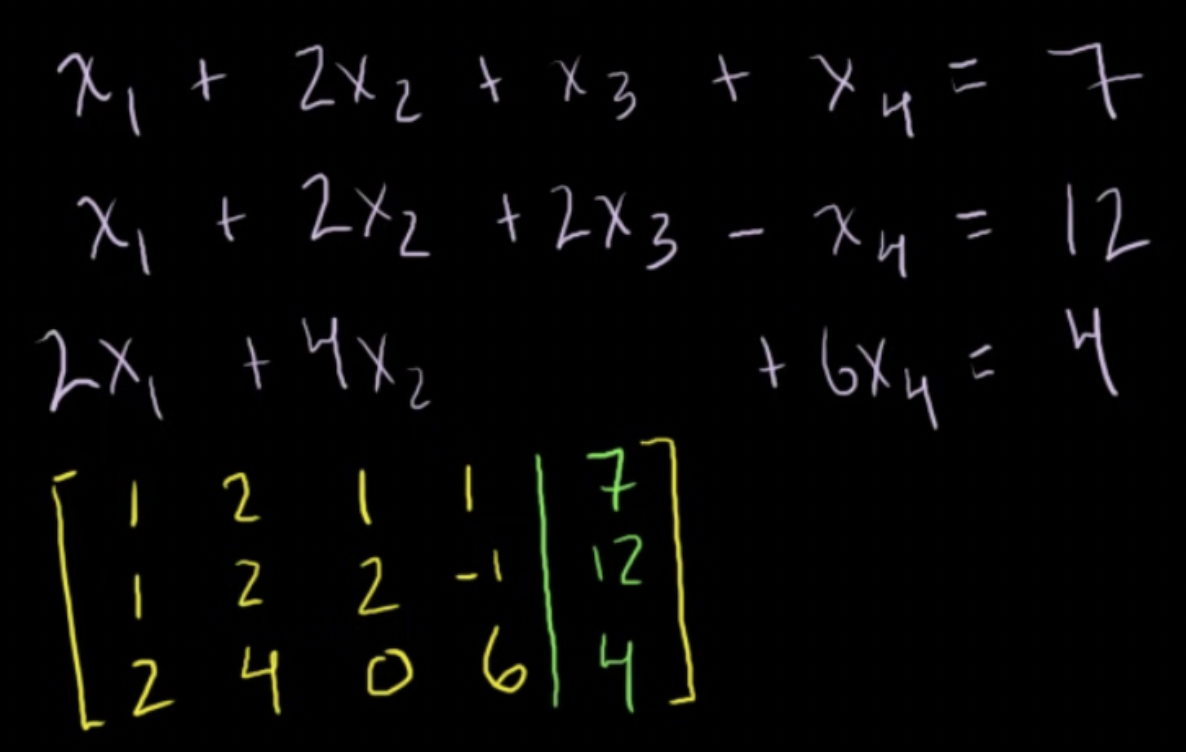
-
기약행사다리꼴(Reduced Row Echelon Form)
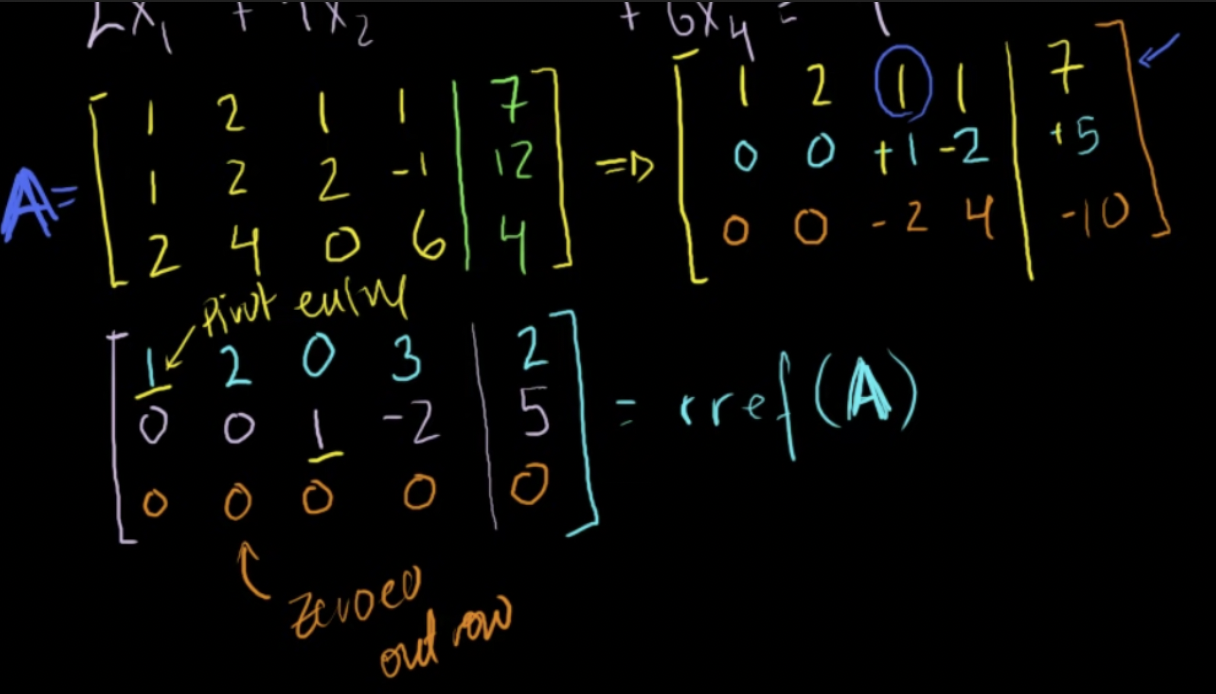
- 피벗 성분(Pivot entry): 각 열에서 유일하게 0이 아닌 수
- zeroed out row: 0으로 된 행, 관례적으로 주로 마지막행에 작성
- 자유변수(Free variables): 피벗성분과 관련 없는 변수
-
4개의 미지수를 가진 3개의 방정식의 해는 R4상의 평면 (Plane in R4)
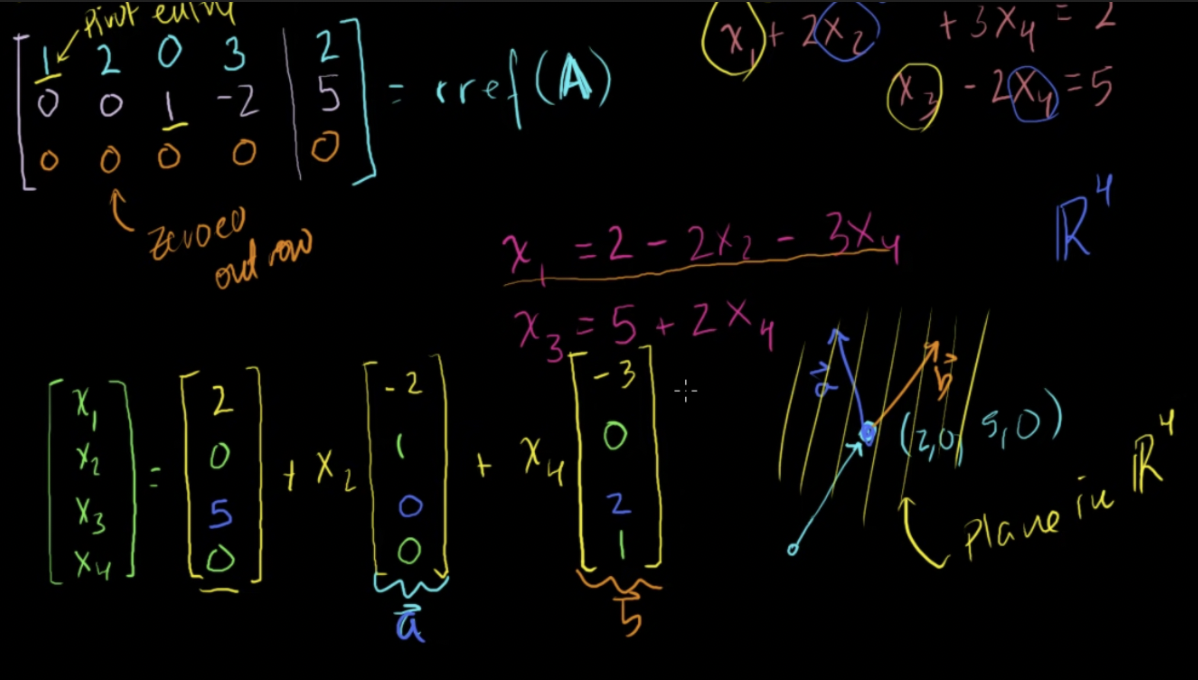
행렬을 이용하여 선형계 풀기
-
첨가행렬(Auggmented Matrix)을 사용해 기약행 사다리꼴로 만들기

-
피벗성분은 열의 유일한 성분
-
각 행의 피벗성분은 이전 행 피벗성분의 오른쪽에 있음
-
자유번수 없음
-
모든 열에 피벗성분이 있음
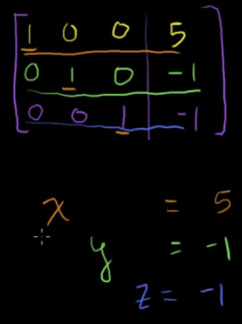
-
행 사다리꼴을 이용하여 선형계는 해가 없다는 것을 알아보기
-
네 개의 변수로 이루어진 세 개의 선형방정식 확대행렬을 이용하여 기약행사다리꼴로 만들기
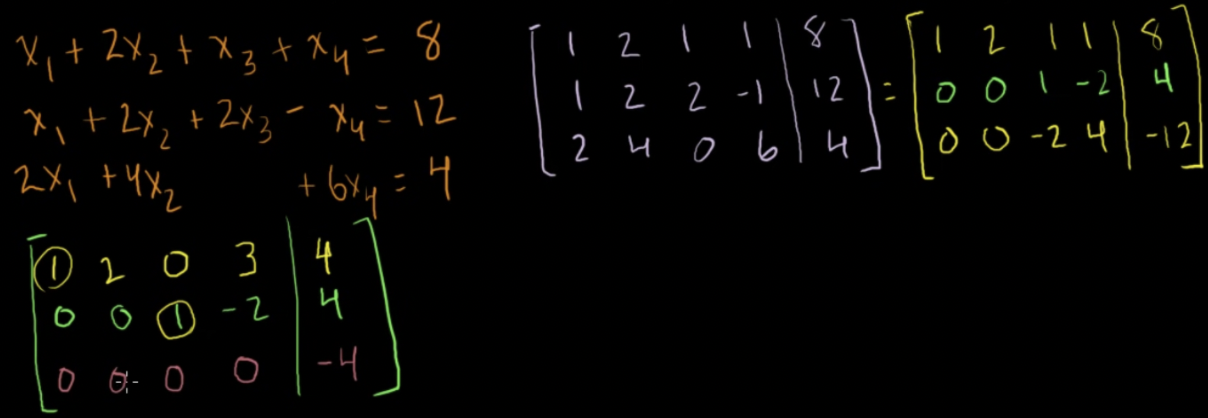
- 각각의 열에서 유일하게 0이 아닌 항인 기준성분 두개가 있음
- 기준성분이 다른 기준성분보다 아래쪽 행의 위치하며 오른쪽 열에 존재함
- 기준성분이 없는 두번째, 네번째 열이 자유변수
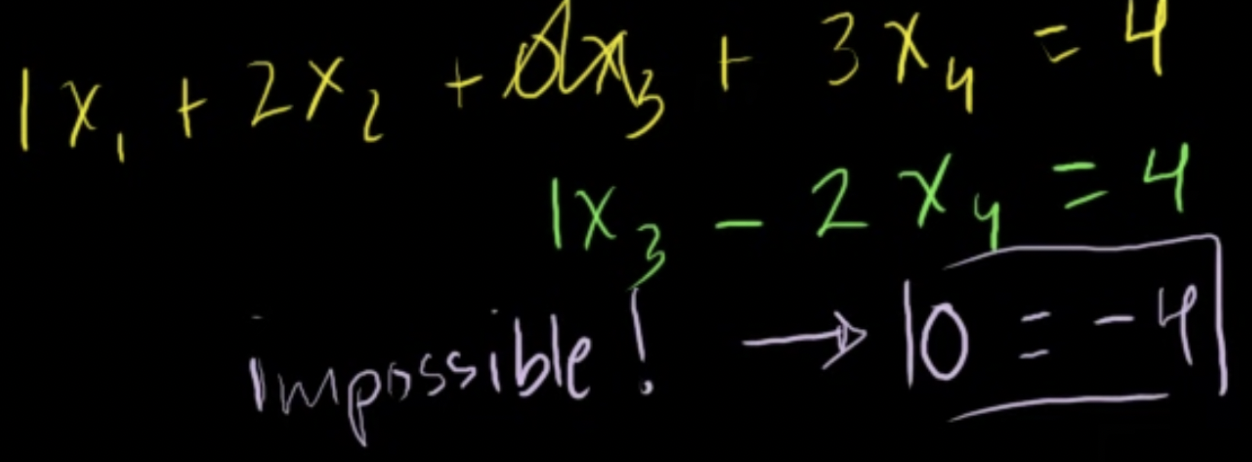
- 0은 -4와 같을 수 없음 (impossible)
- 세개의 연립방성식의 교점, 즉 세 식을 모두 만족하는 답을 찾는 것은 불가능함
- 4차원의 공간에서 교차하지 않는 것
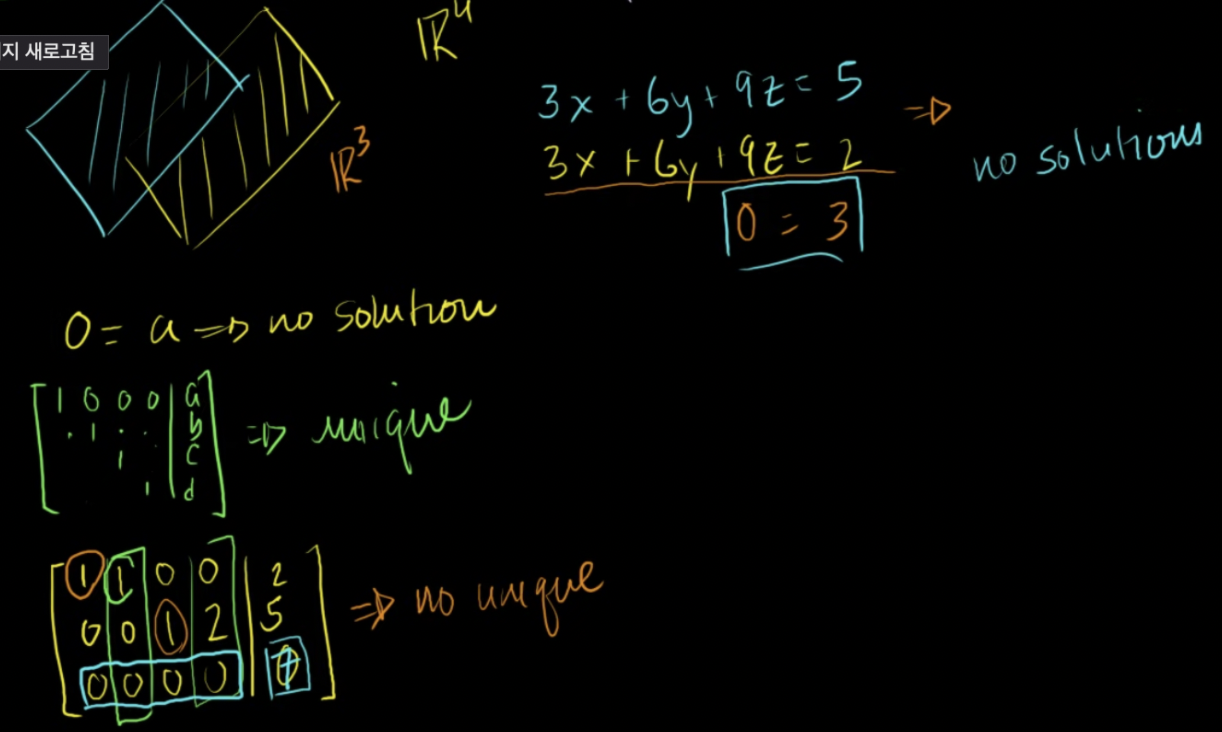
- 0이 어떤것과 같다는 식은 ‘해가 없다는 것’ (no solution)
- 기준 성분이 열의 개수만큼 존재한다면 유일한 해가 존재함(unique solution)
- 자유변수가 있고 마지막행이 전부 0 이라면 무한한 해를 가짐 (No unique solution)
- 모든 항목이 0일 경우에만 자유변수가 존재하고, 무한한 해를 가짐