강화학습기초(1) - MDP, Bellman Equation

본 글은 DeepMind David Silver 교수님의 UCL 강의와 RLCode 이웅원님의 Fundamental of Reinforcement Learning 자료를 기반으로 공부한 내용을 요약한 것이다.

Reinforcement Learning

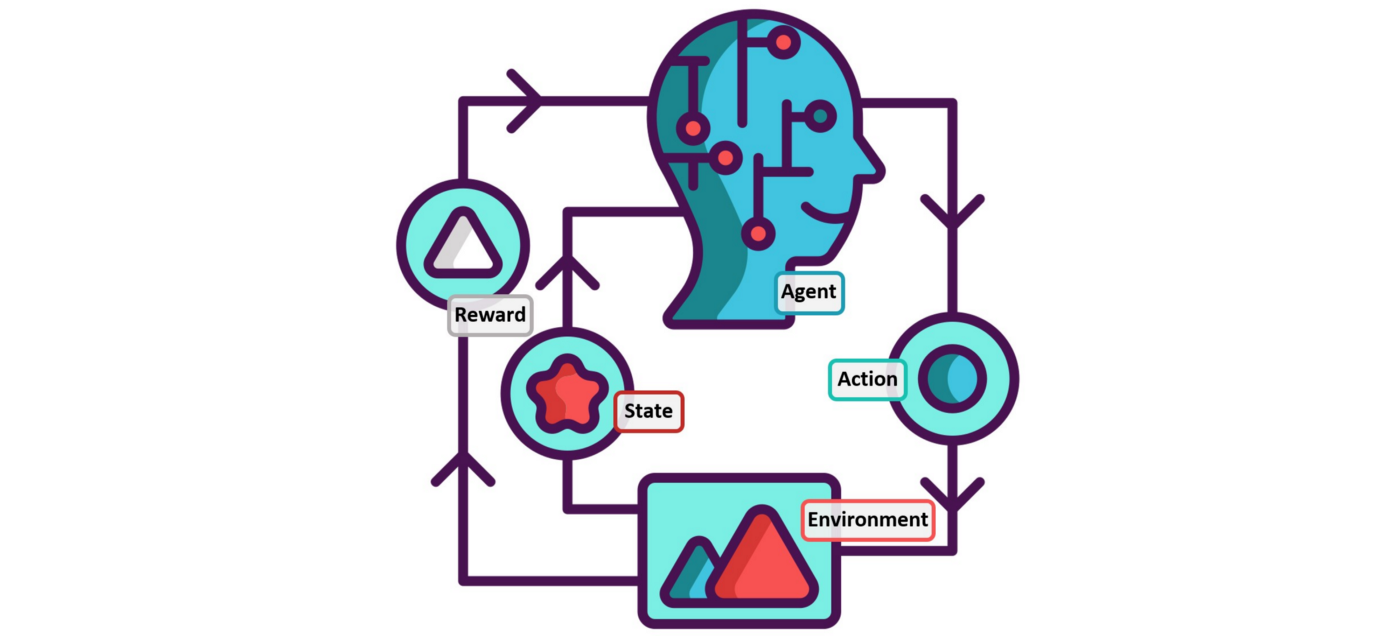
강화학습(Reinforcement Learning)이란, 아래와 같이 environment와 상호작용을 주고 받는 agent가 reward 값을 기반으로 특정 기능을 수행할 수 있도록 학습하는 방식의 일종이다.

Time-step $t$에서,
1. Environment는 agent에게 state $s_t$를 제공한다.
2. Agent는 이에 따라 action $s_t$를 선택한다.
3. Environment는 $(s_t$, $a_t)$에 따른 reward $r_{t+1}$와 다음 state $s_{t+1}$을 제공한다.

Markov Decision Process (MDP)

이 때, environment에서 제공하는 immediate reward $r_{t+1}$이 현재 state $s_t$와 action $a_t$에만 의존하는 경우(time-step $t$ 이전의 값들과는 무관한 경우), 이를 Markov Decision Process (MDP)라고 일컫는다. 앞으로의 모든 내용은 기본적으로 MDP임을 가정한다.

Markov property
: Current state completely characterizes the state of the world.

MDP는 <S, A, R, P, $\gamma$>의 tuple로 정의되며, 각 구성성분의 정의는 아래와 같다.

• S : 가능한 모든 state의 집합

• A : 가능한 모든 action의 집합

• R : 현재 (state, action) 쌍에 대한 immediate reward의 분포

• P : 현재 (state, action) 쌍에 대한 다음 state의 분포 (transition probability)

• $\gamma$ : Discount factor (0~1)
  *0에 가까울수록 당장의 reward에 더 큰 가치를 매겨 근시안적인 판단을, 1에 가까울수록 미래의 reward에 큰 가치를 매겨 미래지향적인 판단을 내릴 수 있다.

특히, 분포 $R$과 $P$를 수식으로 나타내면 아래와 같다.
(Notation에 대해 덧붙이자면, $S_{t}$, $A_{t}$, $R_{t}$ 등과 같은 대문자는 time-step $t$에 해당하는 값들이 담기는 placeholder, 즉 random variable이다. 반면 $s$, $a$ 등과 같은 소문자는 specific value를 의미한다.)

Tradition probability $P_{ss'}^a$의 값이 1이 아닌 경우는 noise가 포함된 stochastic world로 이해하면 좋다. 예를 들어, 격자 상의 agent가 위로 이동하는 action을 취하였더라도 미지의 외부 요인으로 다른 방향으로 움직이거나 움직이지 않는 등의 결과로 이어질 수 있는 경우가 해당된다.

한편, state $S_t$로부터 최종 state에 도달할 때까지 얻어지는 모든 reward를 고려한 값을 return $G_t$라고 하며, discount factor $\gamma$를 통해 cumulative discounted reward의 형태로 아래와 같이 정의된다.

이러한 MDP에 놓이는 agent는 정해진 policy $\pi$에 따라 action을 선택하게 된다. 보통 deterministic(action이 한가지로 결정)하기보단 stochastic(각 action을 선택할 확률로 표현)한 경우가 많으며, 이를 수식으로 표현하면 아래와 같다.

따라서, 강화학습은 최대의 return을 받게 하는 optimal policy $\pi$*를 찾는 과정이라고도 볼 수 있다.
(변수 뒤에 붙는 '*'는 optimum을 의미한다.)

Optimal policy $\pi$*
$\pi^*=\argmax_\pi E[\sum_{t\ge0}\gamma^tR_t|\pi]$    with $S_0$~$P(\cdot)$, $A_t$~$\pi(\cdot|S_t)$, $S_{t+1}$~$P(\cdot|S_t,A_t)$

Value Function

Agent가 최대의 reward를 받는 optimal policy를 탐색하기 위해선 각 time-step의 state와 action의 가치를 판단할 수 있는 지표가 있어야 한다. 그에 해당하는 것이 아래의 두 value function이다.

Value function (State-value function)
$V^\pi(s)= E[\sum_{t \ge 0} \gamma^t r_t|s_0=s,\pi]$

Q-value function (Action-value function)
$Q^\pi(s, a)= E[\sum_{t \ge 0} \gamma^t r_t|s_0=s,$ $a_0=a,$ $\pi]$

앞으로 자주 사용될 함수들이며, 각각 state-value function, Q-value function이라고 명칭을 통일하도록 하겠다.

State-value function의 경우, 1) state $s$로부터 2) policy $\pi$를 따랐을 때 얻게 될 cumulative reward의 기댓값이다. 쉽게 말해, 'state $s$의 long-term value'라고 볼 수 있다.

반면 Q-value function의 경우, 1) state $s$에서 2) action $a$를 선택하고 3) 이후 policy $\pi$를 따랐을 때 얻게 될 cumulative reward의 기댓값이다. 즉, '$(s, a)$ 쌍의 long-term value'라고 볼 수 있겠다.

Stochastic world의 기댓값에 해당하는 위 value function들에 대해, 아래와 같이 optimal value function도 정의할 수 있다.

Optimal state-value function
$V^*(s)=$ $\max_\pi$$E[\sum_{t \ge 0} \gamma^t r_t|s_0=s,\pi]$
          $= E[\sum_{t \ge 0} \gamma^t r_t|s_0=s$$,\pi^*$$]$

Optimal Q-value function
$Q^*(s, a)=$ $\max_\pi$$E[\sum_{t \ge 0} \gamma^t r_t|s_0=s,a_0=a,\pi]$
             $=E[\sum_{t \ge 0} \gamma^t r_t|s_0=s,a_0=a$$,\pi^*$$]$

Bellman Equation

이처럼 정의된 value-function들에 대한 유용한 관계식이 바로 아래의 Bellman equation이다. 연속된 두 time-step의 value function에 대한 점화식임을 쉽게 확인할 수 있다.

Bellman equation of state-value function
$v_\pi(s)$ $=E_\pi[R_{t+1}+\gamma$$v_\pi (S_{t+1})$$|S_t=s]$                 (expectation)
         $=\sum_{a \in A}\pi(a|s)(R_s^a+\gamma\sum_{s'\in S}P_{ss'}^a$$v_\pi(s')$$)$
$v_*(s)$ $=\max_\pi v_\pi(s)=\max_aq_*(s,a)$                   (optimality)
         $=\max_a(R_s^a+\gamma\sum_{s'\in S}P_{ss'}^a$$v_*(s')$$)$

Bellman equation of Q-value function
$q_\pi(s,a)$ $=E_\pi[R_{t+1}+\gamma$$q_\pi(S_{t+1},A_{t+1})$$|S_t=s, A_t=a]$      (expectation)
            $=R_s^a+\gamma\sum_{s'\in S}P_{ss'}^a\sum_{a'\in A}\pi(a'|s')$$q_\pi(s',a')$
$q_*(s,a)$ $=\max_\pi q_\pi(s,a)$                                                (optimality)
             $= R_s^a+\gamma\sum_{s'\in S}P_{ss'}^a\max_{a'}$$q_*(s',a')$

다음 글에서 다루게 될 dynamic programming을 비롯해 모든 강화학습 방식에서 기본적으로 활용되는 중요한 관계식이다. 특히, optimality equation은 policy $\pi$와 무관함을 기억하자.

---

References

• UCL Course on RL, David Silver
• Reinforcement Learning: An Introduction, Richard S. Sutton
• Fundamental of Reinforcement Learning, 이웅원