강화학습기초(2) - Dynamic Programming

본 글에서는 강화학습의 가장 고전적인 방식에 해당하는 dynamic programming(DP) 기법에 관해 다뤄보도록 하겠다.

Dynamic Programming

Dynamic programming이란, 최적화 이론의 한 기술로서 큰 문제를 작은 부분 문제로 나누어, 과거에 구한 부분 문제의 결과를 활용해 큰 문제를 해결하는 방식의 알고리즘을 총칭한다.

주어진 MDP에 대한 optimal policy를 구하는 강화학습에도 dynamic programming을 적용할 수 있는데, policy에 대한 의존성에 따라 1) Policy iteration과 2) Value iteration으로 구분된다. 또한 해당 방식에선 MDP의 (S, A, R, P, $\gamma$)에 대한 모든 정보를 알고 있다고 가정한다. (이는 dynamic programming의 커다란 제약 조건이기도 하다.)

Policy Iteration

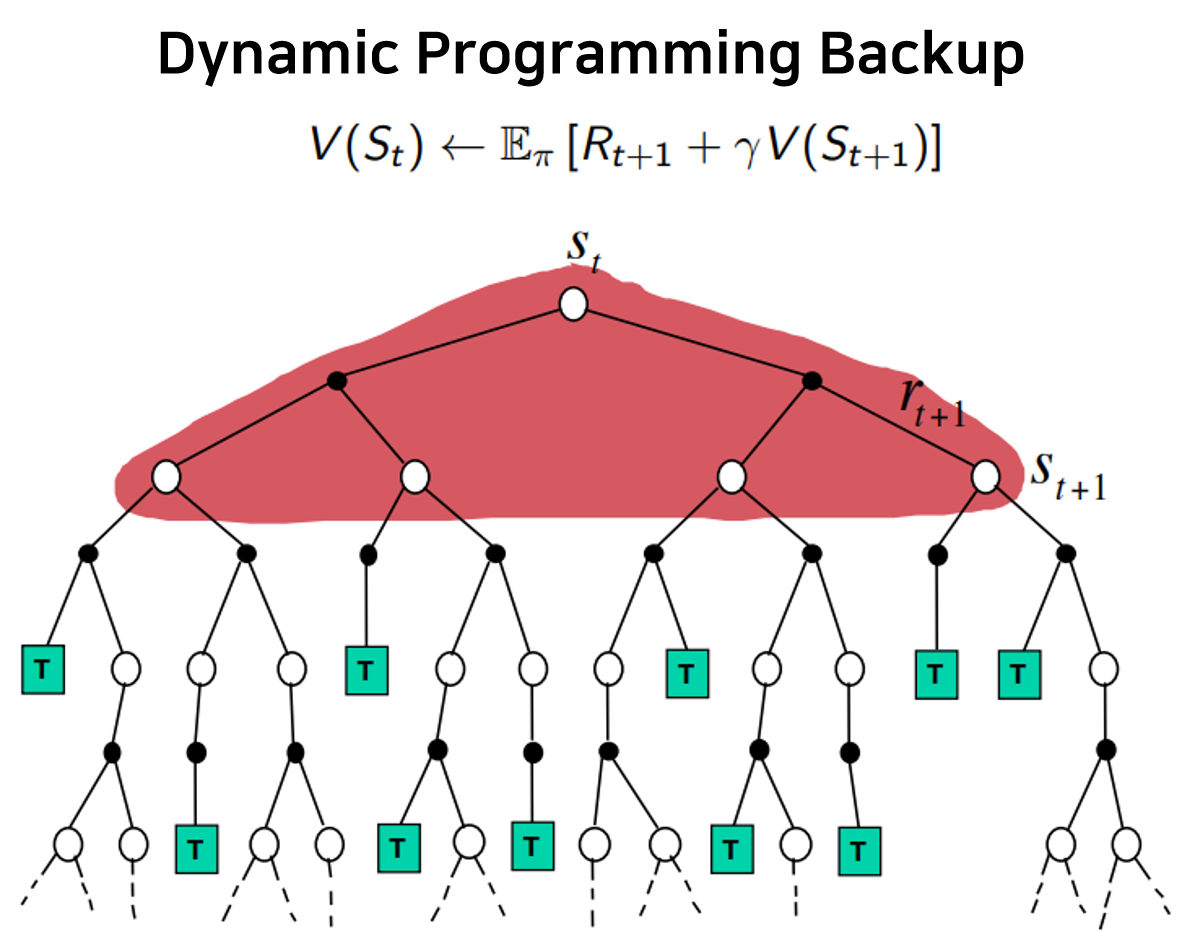
현재 policy $\pi$에 대해, Bellman expectation equation으로 value function을 update하는 방식이다.

우선 초깃값은 zero-initialized value function과 random policy로 두며(보통 각 state에서 가능한 action에 대해 확률값이 모두 동일하도록 초기화), 아래 Bellman equation을 통해 모든 state의 value function을 동시다발적으로 update한다.

위 식에서 유의해야 할 점은 value $v(s)$의 아랫첨자로 iteration number $k$가 추가되었다는 것인데(time index가 아님에 유의하자), 한 번의 update가 한 번의 iteration에 해당한다. 즉, k-th iteration의 값들로 (k+1)-th iteration의 값들을 계산하는 것이다.

이러한 iteration을 여러 번 반복하면 true value function에 점차 수렴하게 되는데, 이를 evaluation이라고 하며, 충분한 iteration 만큼의 evaluation을 거친 후 policy $\pi$를 update하는 과정을 improvement라고 한다. (이는 MDP에 대한 완전한 정보가 보장된 planning에서의 용어로, 추후 다룰 learning에서는 각각 prediction과 control이라는 용어를 사용한다.)

Policy improvement의 경우, state $s$에 대해 $R_s^a+\gamma P_{ss'}^av_k(s')$이 가장 큰 state $s'$으로의 action $a$를 선택하는 greedy algorithm으로 진행된다. 해당 값이 같은 state가 다수 존재할 경우, 균일한 확률분포를 가지게 된다.

이후, 수정된 policy $\pi'$에 대해 다시 value evaluation과 policy improvement을 반복하여 수행하게 되며, 이를 통해 update된 policy $\pi$는 점차 optimal policy $\pi^*$로 수렴하게 된다.

Policy Iteration : Evaluation $\rarr$ Improvement $\rarr$ Evaluation $\rarr$ $\cdot$$\cdot$$\cdot$

Value Iteration

Policy iteration과는 달리, 현재의 policy와 무관한 Bellman optimality equation을 이용하여 value function을 maximize하는 방향으로 update를 진행하는 방식이다.

다시 말해, policy iteration에서는 모든 action에 대한 return 값으로 policy의 probability distribution에 따른 기댓값을 계산했다면, value iteration에서는 최대의 return을 가져오는 action 한 가지의 return 값만을 반영하는 것이다.

이 또한 모든 state의 value function은 zero-initialize 해주며(policy는 별도로 고려해주지 않음), 아래 Bellman equation을 통해 모든 state의 value function을 동시다발적으로 update한다.

이러한 value iteration의 특징은 evaluation 단계에서 충분한 iteration을 거쳐 value update를 수행하면 단 한 차례의 evaluation 만으로도 optimum에 도달할 수 있다는 것이다. Maximum return을 얻는 방향으로만 value function이 반복되어 계산되고, 결국 각 state의 value function을 계산할 때 택한 action의 방향으로 policy가 결정되리란 것을 쉽게 예상할 수 있다.

Value Iteration : Evaluation $\rarr$ Improvement

앞서 살펴본 DP 기법은 MDP에 대한 모든 정보를 가지고 있어야 가능한 planning으로, environment로부터 전달되는 reward만을 가지고 optimal policy를 estimate하는 learning과는 다르다. 또한, evaluation 단계에서의 계산량이 state의 개수에 exponential하게 증가하는 curse of dimensionality에 빠지게 되는 한계점이 있다.

이에, 다음 글에서는 MDP가 상당히 크거나 완전히 알지 못하는 경우 사용할 수 있는 Monte-Carlo learning에 대해 다뤄보고자 한다.

---

References

• UCL Course on RL, David Silver
• Reinforcement Learning: An Introduction, Richard S. Sutton
• Fundamental of Reinforcement Learning, 이웅원