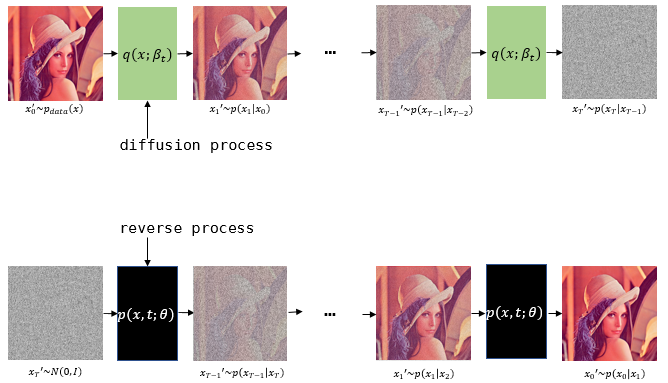
Stable Diffusion(2) - Diffusion Models

구명규·2023년 3월 10일

Diffusion Models

'23 Individual Research

목록 보기

2/19

Stable diffusion이 나오기 전, diffusion model의 근간을 이룬 논문들을 소개하며 기본적인 개념을 다뤄보도록 한다.

1. 'Deep Unsupervised Learning using Nonequilibrium Thermodynamics' (Sohl-Dickstein et al., ICML 2015)

: Diffusion probabilistic process를 비지도학습을 위한 방법론으로 처음 활용한 논문으로, Flexibility와 tractability를 동시에 만족하는 생성 모델을 제안하였다.

1. Introduction

Input으로부터 단번에 latent vector를 얻어내는 것이 아닌, small perturbation(Markov diffusion kernel)을 여러 번 적용하여 tractable하게 만드는 방식이다.
어떠한 target distribution도 diffusion process로 capture 가능하다.
"We restrict the forward (inference) process to a simple functional form, in such a way that the reverse (generative) process will have the same functional form."

2. Algorithm

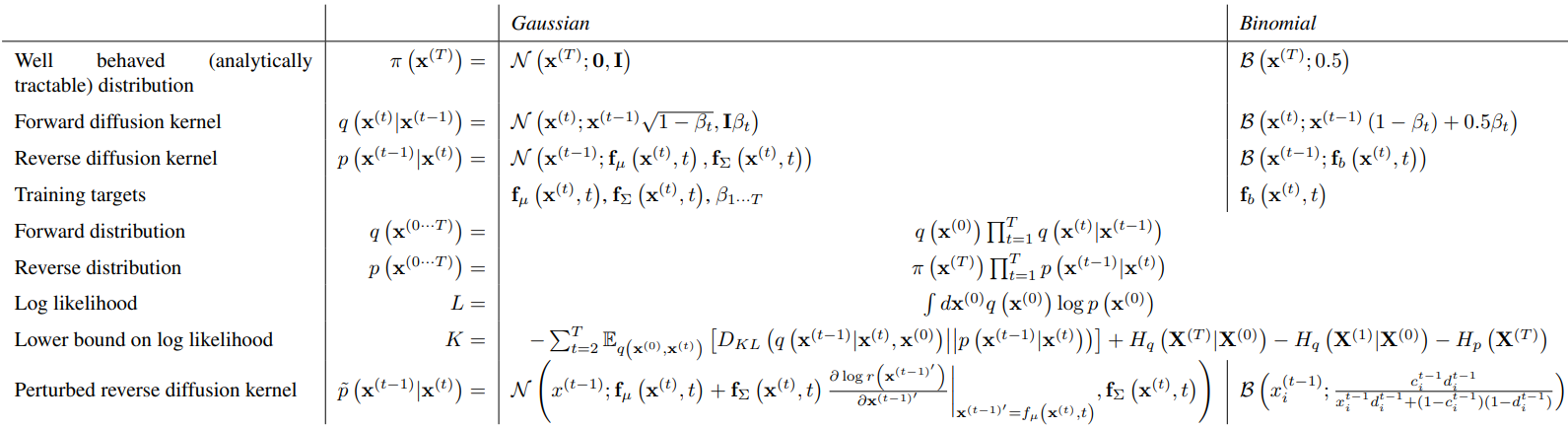
Forward(inference) diffusion process : Repeated application of a Markov diffusion kernel $q(x^{(t)}|x^{(t-1)})$ with diffusion rate, $\beta_t$ .
$\rarr$ Gaussian diffusion into a Gaussian distribution with identity-covariance, or binomial diffusion into an independent binomial distribution(bit flip)

Reverse generative distribution : Forward process의 reverse trajectory로, $p(x^{(t-1)}|x^{(t)})$ kernel의 repeated application.
$\rarr$ $q$ 가 작은 $\beta_t$ 값의 Gaussian(binomial) distribution을 갖는다면 $p$ 는 $q$ 와 identical functional form을 가진다(Tragectory가 길수록 $\beta$ 의 값은 작아짐). 즉, $q$ 도 Gaussian(binomial)로 설정 가능하다.
Training: Model log likelihood $L=E[log\text{ }p(x^{(0)})]=\int dx^{(0)}q(x^{(0)})log\text{ }p(x^{(0)})$ 를 maximize하도록 학습한다. Lower bound strategy( $L\ge K$ )를 사용한다.
$\rarr$ $\hat{p}(x^{(t-1)}|x^{(t)})=argmax_{p(x^{(t-1)}|x^{(t)})}\text{ }K$ ,
$\text{ }\text{ }\text{ }\text{ }K=-\sum_{t=2}^T\int dx^{(0)}dx^{(t)}q(x^{(0)},x^{(t)})D_{KL}(q(x^{(t-1)}|x^{(t)},x^{(0)})||p(x^{(t-1)}|x^{(t)}))$
$\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }+H_q(X^{(T)}|X^{(0)})-H_q(X^{(1)}|X^{(0)})-H_p(X^{(T)})$

$\Rarr$ Forward diffusion에서의 diffusion rate $\beta_t$ 와, reverse diffusion에서 각각 mean과 covariance를 출력하는 함수 $f_\mu(x^{(t)},t)$ 와 $f_\Sigma(x^{(t)}, t)$ 가 $K$ 를 maximize하도록 학습!
Denoising이나 inpainting을 위해선 모델 분포 $p(x^{(0)})$ 에 bounded positive function $r(x^{(0)})$ 를 곱해야 하는데( $\hat{p}(x^{(0)})\propto p(x^{(0)})r(x^{(0)})$ ), 두 분포를 곱하는 것은 costly & difficult하다. 하지만 diffusion model에서는 각 step에서의 small perturbation으로 간주하여 단순화가 가능하다. 본 논문에서는 이를 time-step에 따라 constant하게 두었다.

2. 'Denoising Diffusion Probabilistic Models' (Ho et al., NeurIPS 2020)

: a.k.a. DDPM. 기존 diffusion model의 $L_{t-1}$ loss term과 parameter estimation 과정을 더 학습이 잘 되는 방향으로 발전시켰다.

1. Introduction

본 논문은 diffusion model이 high quality sample을 생성하는 capability를 보여주었다는 것에 의의를 둔다.
특정 parameterization of diffusion models가 denoising score matching과 동일하다는 것을 보였다.

2. Background

: 역시나 true data distribution $p_\theta(x_0)$ 를 학습하는 것이 목표이다.

Forward(diffusion) process : Posterior $q(x_{1:T}|x_0)$
$q(x_{1:T}|x_0):=\prod_{t=1}^Tq(x_t|x_{t-1}),$ $q(x_t|x_{t-1}):=N(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_tI)$
*Variance 값을 1로 유지 + 임의의 timestep $t$ 에 대한 $x_t$ sampling 가능
: $q(x_t|x_0)=N(x_t;\sqrt{\overline{\alpha}_t}x_0, (1-\overline{\alpha}_t)I)$ , $\text{ }\text{ }\alpha_t:=1-\beta_t$ , $\overline\alpha_t:=\prod_{s=1}^t\alpha_s$
Reverse process : Joint distribution $p_\theta(x_{0:T})$
$p_\theta(x_{0:T}):=p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t),$ $p_\theta(x_{t-1}|x_t):=N(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))$
Variational lower bound on negative log likelihood
$L:=E_q[D_{KL}(q(x_T|x_0)||p(x_T))+\sum_{t>1}D_{KL}(q(x_{t-1}|x_t,x_0)||p_\theta(x_{t-1}|x_t))-log\text{ }p_\theta(x_0|x_1)]$
$\text{ }\text{ }\text{ }\rarr L_T$ (regularization term) $+L_{t-1}$ (denoising process term) $+L_0$ (reconstruction term)
* $q(x_{t-1}|x_t)$ 는 intractable하나 $q(x_{t-1}|x_t, x_0)$ 는 tractable!

3. Diffusion models and denoising autoencoders

Forward process : Diffusion rate $\beta_t$ 를 고정시켜 parameter의 학습이 이뤄지지 않는다.
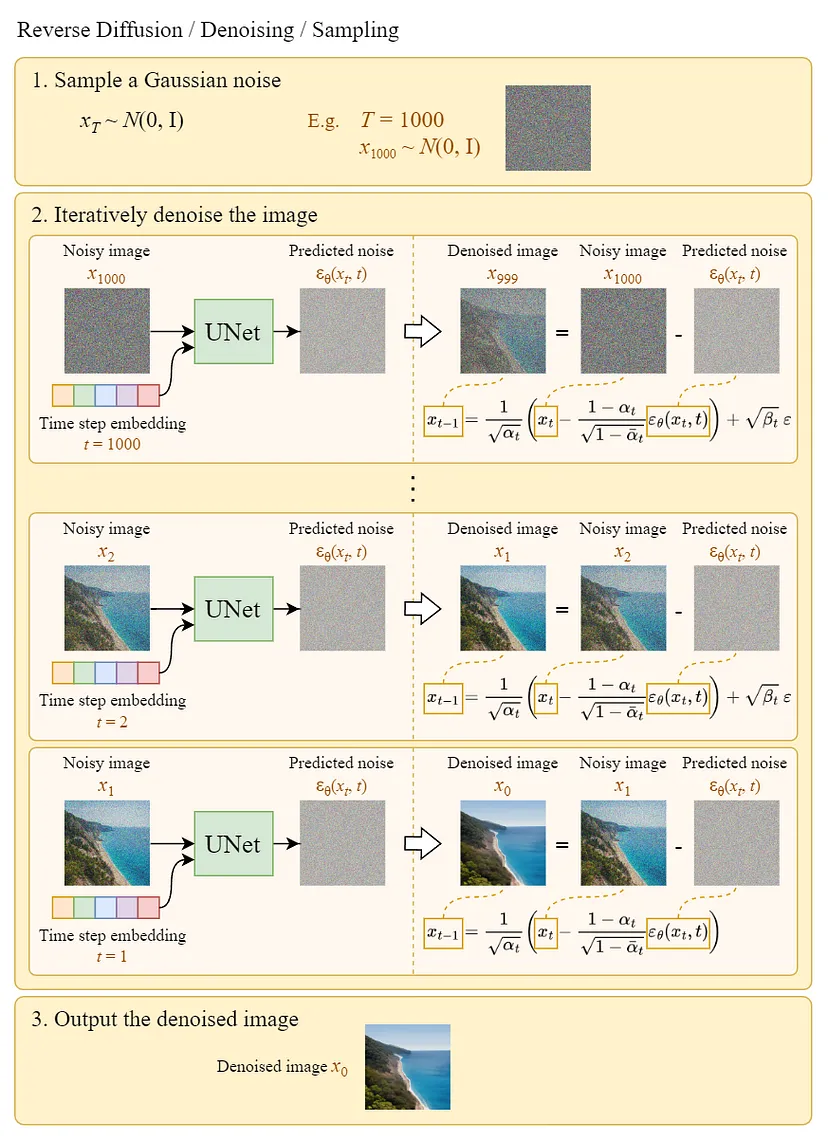
Reverse process : $p_\theta(x_{t-1}|x_t)=N(x_{t-1};\mu_\theta(x_t,t),\Sigma_\theta(x_t,t))$
- $L_T$ (regularization term) : Forward process $q$ 와 $p(x_T)$ 를 각각 untrained parameter를 가지는 정규분포로 가정했기 때문에 $L_T$ term으로는 학습이 진행되지 않는다.
  (Fixed noise scheduling으로도 충분히 많은 diffusion kernel을 통해 'isotropic Gaussian' latent space를 획득할 수 있어 regularization이 불필요하다.)
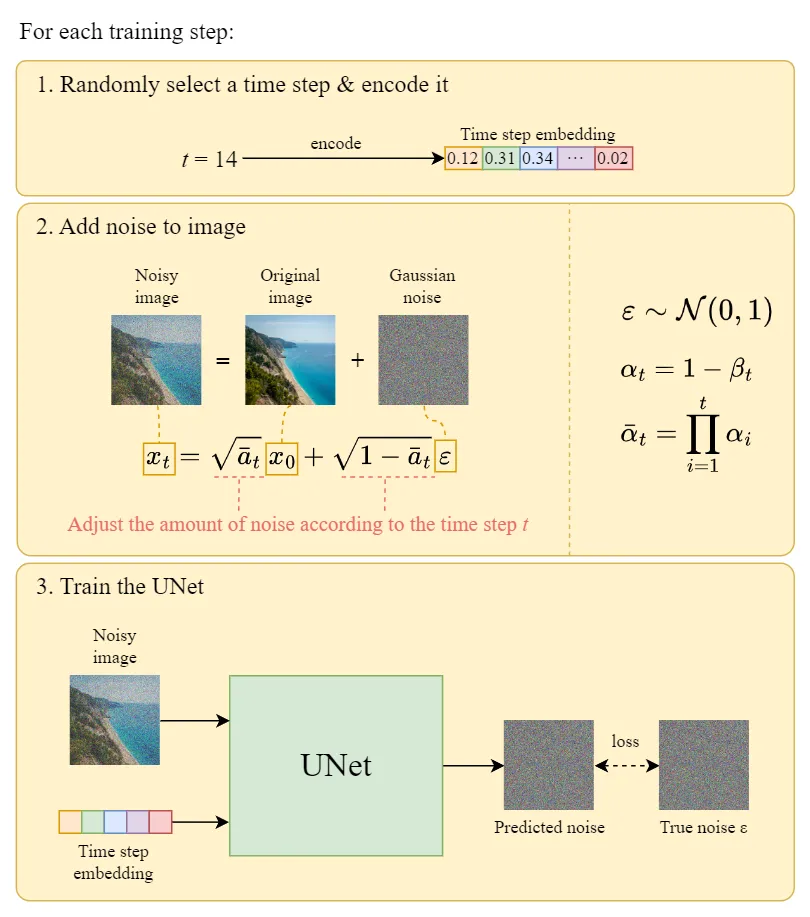
- $L_{t-1}$ (denoising process term) : 1) $q(x_{t-1}|x_t,x_0)$ 와 $p_\theta(x_{t-1}|x_t)$ 를 구성하는 2) $\mu_\theta$ , 3) $\Sigma_\theta$ 를 구해야 한다.
  - $q(x_{t-1}|x_t,x_0)$ $=N(x_{t-1};\tilde\mu_t(x_t,x_0),\tilde\beta_tI)$ ,
    where $\tilde\mu_t(x_t,x_0):=\frac{\sqrt{\overline\alpha_{t-1}}\beta_t}{1-\overline\alpha_t}x_0+\frac{\sqrt{\alpha_t}(1-\overline\alpha_{t-1})}{1-\overline\alpha_t}x_t$ , $\tilde\beta_t=\frac{1-\overline\alpha_{t-1}}{1-\overline\alpha_t}\beta_t$
    and $x_t=\sqrt{\overline\alpha_t}x_0+\sqrt{1-\overline\alpha_t}\epsilon$ (reparameterization)
  - $\Sigma_\theta(x_t,t)$ $=\sigma_t^2I=\tilde{\beta}_tI$ : Untrained time dependent constants
  위 식을 $L_{t-1}$ 항에 대입하면, $\mu_\theta(x_t,t)$ 가 forward process posterior mean인 $\tilde\mu_t(x_t,x_0)$ 를 predict할 때 최소의 loss 값을 가지며, 해당 값에 $x_t$ 의 reparameterization 식을 대입하면 $\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\overline\alpha_t}}\epsilon)$ 로 표현된다. 즉, $x_t$ 는 학습 과정에서 sampling되어 주어지므로, $\mu_\theta(x_t,t)$ 가 $\epsilon$ 의 함수로 나타내어지는 값을 predict해야 한다.
  
  이 때, $x_t$ 로부터 $\epsilon$ 값을 approximate하는 $\epsilon_\theta(x_t)$ 를 정의하여 $\mu_\theta(x_t,t)$ 식을 아래와 같은 denoising matching의 관점으로 새롭게 정의하면,
  
  $\mu_\theta(x_t,t)=\tilde\mu_t(x_t,\frac{1}{\sqrt{\overline\alpha_t}}(x_t-\sqrt{1-\overline\alpha_t}\epsilon_\theta(x_t)))=\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta}{\sqrt{1-\overline\alpha_t}}\epsilon_\theta(x_t,t))$
  
  이며, 이를 다시 $L_{t-1}$ 항에 대입하면, 아래와 같은 loss term이 만들어진다.
  
  $E_{x_0,\epsilon}[\frac{\beta_t^2}{2\sigma_t^2\alpha_t(1-\overline\alpha_t)}||\epsilon-\epsilon_\theta(\sqrt{\overline\alpha_t}x_0+\sqrt{1-\overline\alpha_t}\epsilon,t)||^2]$
- $L_0$ (reconstruction term) $=N(x_0;\mu_\theta(x_1,1),\sigma_1^2I)$
  $\rarr$ 위 $L_{t-1}$ loss term을 통해 충분히 학습 가능하며 무시할 경우 sample quality가 좋아지는 것으로 알려져 있다.

Data scaling, reverse process decoder, and $L_0$
- {0,1, ..., 255}의 픽셀 값을 [-1, 1]의 범위로 scale하였다.
Simplified training objective
- $L_{simple}(\theta):=E_{t,x_0,\epsilon}[||\epsilon-\epsilon_\theta(\sqrt{\overline{\alpha}_t}x_0+\sqrt{1-\overline{\alpha}_t}\epsilon,t)||^2]$
$\rarr$ $t$ 에 dependent한 상수 값을 생략하여 L2 loss와 같은 형태의 objective function을 구하였다. 이는 작은 $t$ 의 loss term에 대해 down-weight하는 효과를 가진다.

*Denoising (sampling) process가 모든 timestep에 대해 진행되므로 매우 느리다는 한계가 존재한다.

4. Experiments

T=1000, linearly increasing constant : $\beta_1=10^{-4}$ to $\beta_T=0.02$
U-Net backbone with group normalization
Simplified objective가 training에서의 codelength는 안좋게 나왔지만 최고의 sample quality를 보여준다. 또한 $\epsilon$ 에 대한 prediction이 해당 objective에 더 적합했다고 한다.

3. 'Denoising Diffusion Implicit Models' (Song et al., ICLR 2021)

a.k.a. DDIM. 기존의 DDPM을 non-Markovian diffusion process에 대해 일반화한 모델이다.
$q(x_t|x_{t-1},x_0)$ 로 process를 재정의하며, $p(x_{t-1}|x_t)$ 의 Gaussian noise $\sigma_𝑡$ 를 0으로 두면 deterministic generative process가 가능해진다. 즉, 임의의 noise에 대한 image가 유일하게 결정된다.
DDPM보다 더 적은 sampling step으로 fast sampling이 가능하며, 요샌 DDPM으로 학습시킨 모델을 DDIM의 generation 방식으로 sampling하는 것이 일반적이다.

4. 'Score-based Generative Modeling with Differential Equations' (Song et al., ICLR 2021)

별개의 방향으로 연구된 'score-based method'가 'diffusion model'과 동일함을 밝힌 논문이다.
Taylor expansion을 통해 $x_t$ 에 대한 sampling 관계식을 아래와 같이 표현 가능하다.
$x_t\approx x_{t-1}-\frac{\beta(t)\Delta t}{2}x_{t-1}+\sqrt{\beta(t)\Delta t}N(0,I)$
위 관계식을 stochastic differential equation(SDE)의 형태로 나타내면, 아래와 같다.
$dx_t=-\frac{1}{2}\beta(t)x_tdt+\sqrt{\beta(t)}d\omega_t$
위 식의 RHS은 앞선 drift term(pulls towards mode) $\beta(t)$ 와 diffusion term(injects noise) $g(t)$ 로 구분 가능하다.
$dx_t=f(t)x_tdt+g(t)d\overline{\omega}_t$

dx_t=[-\frac{1}{2}\beta(t)x_t-\beta(t)\nabla_{x_t}log q_t(x_t)]dt+\sqrt{\beta(t)}d\overline{\omega}_t

핵심은 score function $\nabla_{x_t}\log q_t(x_t)$ 를 optimize 하는 것이며, 이는 intractible하므로 $\nabla_{x_t}\log q_t(x_t|x_0)$ 을 학습하도록 수정하였다.

$\Rarr$ $x_t$ 에 대한 reparameterization으로 수식을 정리하면 기존 DDPM의 loss term과 동일해진다.

위와 같이, diffusion model을 처음으로 제시한 논문과 해당 모델의 실용성을 발전시킨 DDPM, DDIM 논문을 통해 diffusion model의 기초 내용을 다뤄보았다. 다음 글에선 stable diffusion 모델을 다뤄보기 전 마지막으로 conditioning algorithm에 해당하는 attention과 classifier-free conditioning에 대해 살펴보도록 하겠다.