강화학습기초(8) - Advanced Models

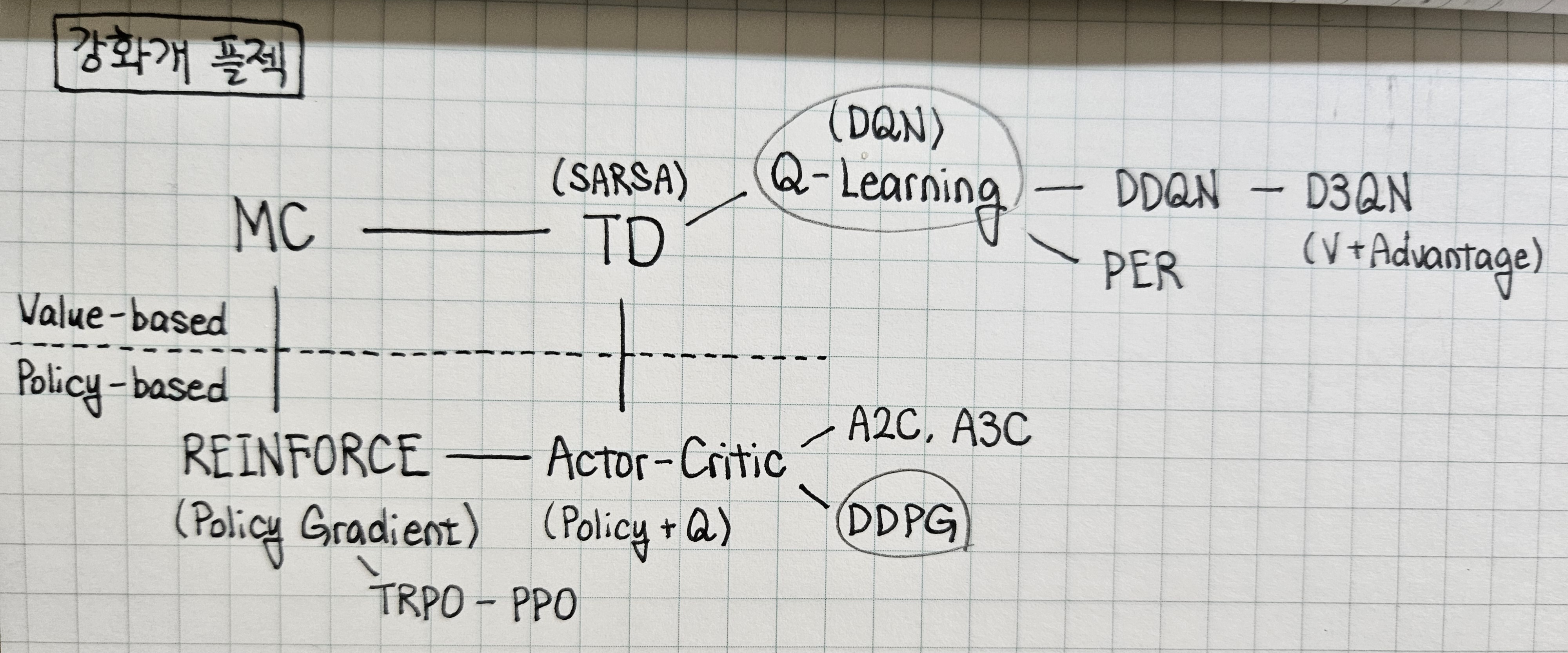
앞선 기본 모델들에 대한 요약 및 DDQN, D3QN, PER, A2C, A3C, PPO, TRPO, DDPG 등의 advanced model에 대한 내용 정리.

Value-based Greedy Algorithms

• Q-value function을 episode마다 return 값으로 근사하는 MC와 time-step마다 immediate reward 값으로 근사하는 TD(SARSA).

- MC : $\Delta w=\alpha ($$G_t$$-\hat{q}(S_t,A_t,w))\nabla_w\hat{q}(S_t,A_t,w)$

- TD(0) : $\Delta w=\alpha ($$R_{t+1}+\gamma \max_{A_{t+1}}\hat{q}(S_{t+1}, A_{t+1},w)$$-\hat{q}(S_t,A_t,w))\nabla_w\hat{q}(S_t,A_t,w)$

- TD($\lambda$) : $\Delta w=\alpha ($$G_t^\lambda$$-\hat{q}(S_t,A_t,w))\nabla_w\hat{v}(S_t,w)$, $G_t^\lambda=(1-\lambda)\sum_{n=1}^\infin\lambda^{n-1}G_t^{(n)}$

• TD 방식의 importance sampling(off-policy)에서 behavior policy와 target policy를 분리한 Q-Learning (DQN).
  • Behavior policy로 $A_t$ 추출한 뒤 target policy로 target $\hat{q}(S_{t+1},A_{t+1},w)$ 추출. 그에 대한 gradient로 behavior policy 학습, 일정 주기마다 target policy로 update(학습에 대한 target을 어느 정도 고정시켜두며 학습 안정화).

Policy-based Algorithms (Policy Gradient)

Policy(action probability) 자체를 estimate하여 학습의 variance를 줄이고 stochastic policy 구현 가능.

• 매 episode마다 return 값으로 policy를 update하는 MC Policy Gradient(REINFORCE).
• 매 time-step마다 immediate reward 값으로 policy를 update하는 TD Policy Gradient(Actor-Critic)
  • 단, 참고할 value function이 없으므로 이를 estimate하는 critic network 설정, experience replay 사용 X.
    - $\Delta\theta_{\text{actor}}=\alpha\nabla_\theta log\pi_\theta(s,a)\text{ }Q_w(s,a)$
    - $\Delta w_{\text{critic}}=\alpha (R_{t+1}+\gamma Q_w(S_{t+1}, A_{t+1})-Q_w(S_t,A_t))\nabla_w Q_w(S_t,A_t)$

Advanced Models

[DQN 후속 모델]

• DDQN (Double DQN)
  : 기존 Q-learning에서 target으로 사용한 $R_{t+1}+\gamma$$\max_{A_{t+1}}$$\hat{q}(S_{t+1}, A_{t+1},w)$는 overestimated target.
  : Target policy의 maximum 대신 behavior policy를 maximize하는 action을 target policy에 입력한 값을 target으로 사용.

  $\max_{A_{t+1}}\hat{q}_{\text{target}}(S_{t+1}, A_{t+1},w) \rarr \hat{q}_{\text{target}}(S_{t+1}, \argmax_{A_{t+1}}\hat{q}_{\text{behavior}}(S_{t+1}, A_{t+1}), w)$

• D3QN (Dueling DQN)
  : Network가 Q-value function이 아닌, state-value function과 advantage function을 출력. (Q-value = State-value + Advantage)
  : 이 때, 1) 모든 action에 대해 advantage function의 평균은 0이다 혹은 2) Greedy policy에 대해 advantage function은 0의 고정값을 가진다라는 prior information을 사용해 advantage function에 대한 parameter를 학습시킴.
  : 이로 인해 매 time-step마다 선택하지 않은 action에 대한 value function의 값도 함께 update됨.

• PER (DQN + Prioritized Experience Replay)
  : 학습 초기 exploration 과정에서의 transition은 가치가 떨어지므로 TD error가 큰 transition일수록 더 많이 추출.
  : 학습 초기엔 TD error가 큰 특정 transition에 더 가중치를 두고, 학습이 진행될수록 점점 고르게 부여하는 importance sampling weight 도입.

---

[Policy Gradient 후속 모델]

• TRPO (Trust Region Policy Optimization)
  : Policy gradient의 성능 정체와 비효율적인 sampling 문제를 해결하고자 loss function 재정의. 특정 constraint 이내에서 'surrogate' objective를 최대화하는 방향으로 policy를 update하는 Trust Region Methods 적용. 어렵다...

• PPO (Proximal Policy Optimization)
  : TRPO와 마찬가지로 importance sampling을 통해 기존의 sample 재사용(probability ratio 추가). TRPO의 복잡한 constraint를 적용하는 대신, policy update의 step size를 제한하는 clipping 적용(first-order method).

---

[Actor-Critic 후속 모델]

• A2C (Advantage Actor-Critic)
  : 기존의 Critic network가 Q-value를 estimate하고, 이를 target으로 삼아 Actor network가 학습됨. 하지만 action-independent한 변수를 더해주어도 loss gradient 값에 영향을 주지 않는다는 점에 착안하여 Actor network를 advantage function으로 학습시키도록 하고, Critic network는 Q-value 대신 이에 필요한 state-value를 estimate하도록 수정. (단, 매 time-step마다 update하지 않고 N개의 sample을 모아 한 번의 update를 진행하고 sample들을 모두 폐기하는 방식 사용.)

• A3C (Asynchronous Advantage Actor-Critic)
  : A2C 모델에서 발생하는 sample간 correlation 문제를 해결하기 위해 고안. 서로 독립적인 환경의 Actor-Learner로 sample을 저장하여, 각 Actor-Learner가 모은 sample로 global network update. Actor-Learner는 다시 global network로부터 자신을 update하며 학습 진행.

• DDPG (Deep Deterministic Policy Gradient)
  : Policy based Actor-Critic algorithm에서, actor network가 각 action에 대한 확률값이 아닌, 특정 action 자체를 출력하도록 수정. Action의 확률 분포에 따른 gradient의 평균값 계산 대신, 정해진 action에 대한 Q-value function의 gradient 계산으로 충분.

• TD3 (Twin Delayed DDPG)
  : Critic network를 하나 더 추가하여 그 중 작은 값으로 actor network update.

• SAC (Soft Actor-Critic)
  : 기존 actor-critic의 loss에 entropy term을 추가.

[Actor-Critic] $\Rarr$ $a_t\sim \pi_\theta(\cdot|s_t)$
Actor: $\theta\larr\theta+\alpha_\theta\gamma^t$$Q_w(s_t,a_t)$$\nabla_\theta ln\pi_\theta(a_t|s_t)$
Critic: $w\larr w+\alpha_w\nabla_wQ_w(s_t,a_t)(r_{t+1}+\gamma Q_w(s_{t+1}, a_{t+1})-Q_w(s_t, a_t))$

[A2C] $\Rarr$ $a_t\sim \pi_\theta(\cdot|s_t)$
Actor: $\theta\larr\theta+\alpha_\theta\gamma^t$$(r_{t+1}+\gamma V_w(s_{t+1})-V_w(s_t))$$\nabla_\theta ln\pi_\theta(a_t|s_t)$
Critic: $w\larr w+\alpha_w\nabla_wV_w(s_t)(r_{t+1}+\gamma V_w(s_{t+1})-V_w(s_t))$

[DDPG] $\Rarr$ $a_t=\pi_\theta(s_k)+e$
Actor: $\theta\larr\theta+\alpha_\theta$$\nabla_\theta Q_w(s, \pi_\theta(s))$
Critic: $w\larr w-\alpha_w\nabla_w(r_{t+1}+\gamma Q_{w^-}(s_{t+1}, \pi_{\theta^-}(s_{t+1}))-Q_w(s_t, a_t))^2$

---

TO DO

• Rainbow (DDQN + PER + ...)

---

References

• 혁펜하임의 “트이는” 강화 학습 (Reinforcement learning)
• 최신 강화학습 알고리즘 요약
• Deep Learning Bible