강화학습기초(7) - Policy Gradient, REINFORCE, Actor-Critic

본 글에서는 강화학습 기초내용의 마지막으로 policy gradient에 대해서 알아보도록 한다.

앞서 다룬 강화학습은 모두 1) value function을 evaluate/predict하고, 2) greedy algorithm으로 policy를 수립하는 value-based 방식였다. 이는 특정 state에 대한 optimal action이 하나로 결정되는 deterministic model을 생성하는데, 가위바위보와 같이 stochastic policy를 갖는 (가위, 바위, 보를 random하게 내는 것이 optimal) 경우엔 위 방법으로는 학습이 불가능하다. 이에 대해 UCL 강의에서 David Silver가 제시한 또 하나의 예시를 살펴보자.

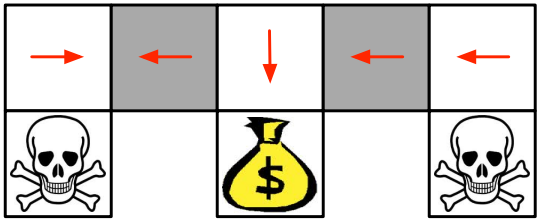
위 그림과 같은 gridworld에서, agent는 해골을 피해 돈주머니를 찾아내야 한다. 하지만 만약 현재 agent가 인접해있는 칸들에 대한 정보만을 state로 정의한다면 회색으로 칠해진 칸들은 동일한 state로 간주된다. 따라서, 정해진 policy에 따라 동일한 action만을 취하게 되고, agent의 시작 위치에 따라 목적지에 결코 도착할 수 없게 된다.

이러한 문제를 해결하기 위해선 회색 칸에서 일정 확률에 따라 양방향으로 모두 움직이는 stochastic policy가 필요하며, 이는 value function을 고려하지 않고 곧바로 policy를 approximate하는 방식인 policy gradient를 통해 해결 가능하다.

Policy Gradient

이전 글에서 살펴본 value function approximation과 달리, policy gradient에선 마찬가지로 approximator를 정의하되, 아래와 같이 value function이 아닌 policy 자체를 approximate하게 된다.

Parameter $w$로 구성되어 value function을 estimate하는 $\hat{v}(S,w)$와 parameter $\theta$로 구성되어 각 action을 수행할 확률에 해당하는 policy를 estimate하는 $\pi_\theta(s,a)$를 서로 구분할 수 있도록 하자.

이러한 policy-based reinforcement learning은 각 action을 택할 확률값을 estimate하므로 선택 가능한 action이 다수거나 action 자체가 연속적인 경우 효과적이다. 또한 value-based 학습보다 안정적인데, 아래에서 구체적으로 살펴보자.

Value-based greedy updates : $\theta_{\pi'}=argmax_\theta E_{\pi_\theta}[Q^\pi(s,a)]$
$V^{\pi_0}\text{ }-$(small change)$\rarr\text{ }\pi_1\text{ }-$(large change)$\rarr V^{\pi_1}\\ \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }-$(large change)$\rarr\text{ }\pi_2\text{ }-$(large change)$\rarr\cdots\\$
Policy gradient updates : $\theta_{\pi'}=\theta_\pi+\alpha\frac{dJ(\theta)}{d\theta}|_{\theta=\theta^\pi}$
$V^{\pi_0}\text{ }-$(small change)$\rarr\text{ }\pi_1\text{ }-$(small change)$\rarr V^{\pi_1}\\ \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }-$(small change)$\rarr\text{ }\pi_2\text{ }-$(small change)$\rarr\cdots$

위와 같이, predicted value function으로 greedy하게 policy를 수립할 경우, value function의 작은 변화에도 선택하게 되는 action이 휙휙 변할 수 있어 학습이 potentially unstable하다. 한편, gradient ascent 방식으로 parameter $\theta$를 incremental하게 update하는 경우 policy의 분포 자체가 smooth하게 변하므로 stable learning을 기대해볼 수 있다.

하지만 policy-based 학습도 local optimum에 빠지기 쉬우며 학습 과정이 inefficient하고 variance가 높다는 단점을 가지고 있다.

한편, value function approximator에 대한 loss function은 아래와 같이 비교적 자명하게 정의할 수 있었다.

하지만 policy approximator를 학습시키기 위한 loss function (objective function) $J(\theta)$는 아래와 같이 MDP의 조건에 따라 다양하게 구성해볼 수 있다.

1. 종료 state가 결정되는 episodic environment의 경우, start value를 사용
   : $J_1(\theta)=V^{\pi_\theta}(s_1)=E_{\pi_\theta}[v_1]$
   
   
2. 종료 state 없이 계속 진행되는 continuing environment의 경우, average value를 사용
   : $J_{avV}(\theta)=\sum_s d^{\pi_\theta}(s)V^{\pi_\theta}(s)$
   혹은, average reward per time-step을 사용
   : $J_{avR}(\theta)=\sum_s d^{\pi_\theta}(s)\sum_a\pi_\theta(s,a)R_s^a$

이 때, $d^{\pi_\theta}(s)$는 'stationary distribution of Markov chain for $\pi_\theta$'로, 아래와 같이 정의되며, 충분한 time-step이 지났을 때, 각 state $s$에 머무를 확률 분포라고 볼 수 있다.

위에서 정의된 objective function을 하나씩 살펴보면, 우선 start value $J_1(\theta)$의 경우, 정해진 초기 state $s_1$에 대해, 이로부터 예상되는 whole episode return의 기댓값임을 알 수 있다. 한편 average value $J_{avV}(\theta)$는 모든 state에 대해 예상되는 return의 평균값이며, average reward per time-step $J_{avR}(\theta)$는 모든 state에 대해 예상되는 immediate reward의 평균값이라고 볼 수 있다. 그렇다면 이러한 loss function에 대한 학습은 어떻게 진행할 수 있을까.

Finite Difference Policy Gradient

가장 직관적으로, 아래와 같이 n-dimension의 parameter vector $\theta$에 대해, 각 성분을 $\epsilon$만큼 변화시켜가며 n개의 성분에 대한 gradient 값을 각각 구하는 numerical한 방법을 생각해볼 수 있다.

이는 policy가 미분가능하지 않더라도 사용 가능하며, 단순한 MDP 내에선 충분한 학습성능을 보인다. 하지만, parameter space가 커질수록 학습이 noisy해지고 inefficient해진다는 단점이 있다.

따라서 이번엔 policy가 미분가능하다는 전제 하에, episode마다 gradient를 직접 구해주는 analytical한 방식을 살펴보도록 하자.

Score Function

앞서 정의한 average reward per time-step에 대해, parameter $\epsilon$에 대한 gradient 값을 유도해보자. 아래와 같이, log 함수에 대한 미분 형태로 바꿔주면 gradient of log probability에 대한 기댓값으로 표현할 수 있다.

위 gradient 식에서 parameter $\theta$의 update 방향을 제시하는 $\nabla_\theta log\pi_\theta(s,a)$ 항을 score function이라 칭하며, 이는 아래 그림과 함께 해석해볼 수 있다.

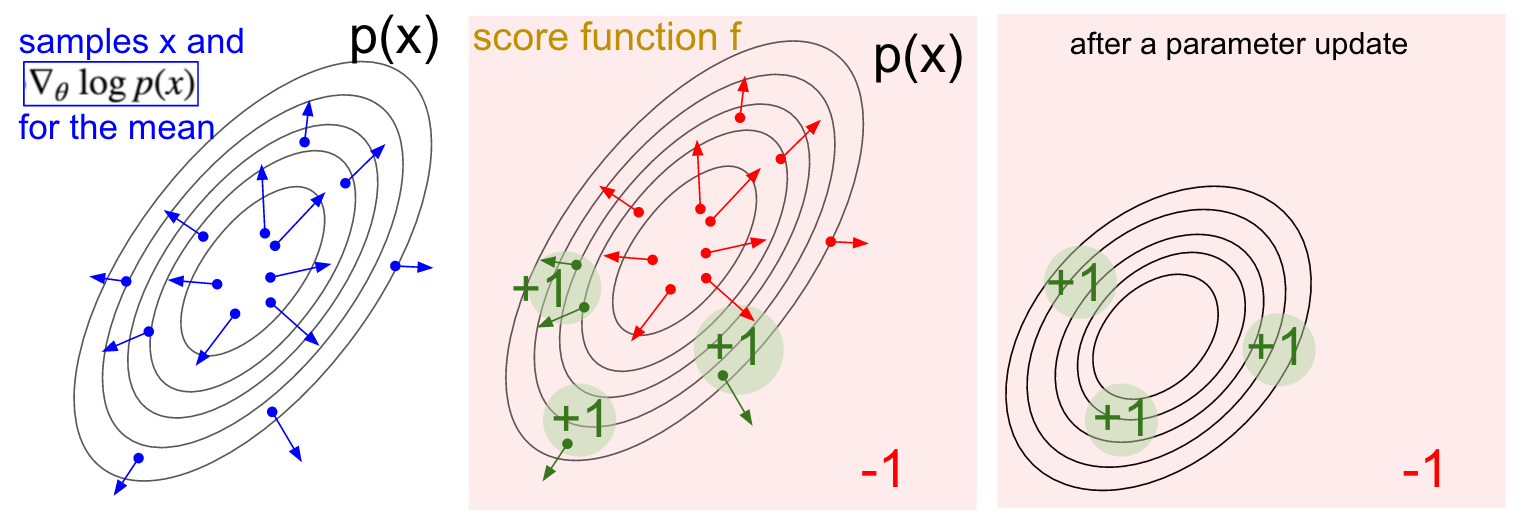
왼쪽 그림은 Gaussian distribution $p(x)$를 따르는 $x$를 sampling한 뒤, log probability의 gradient vector를 표시한 것으로, $p(x)$를 policy approximator $\pi_\theta(s,a)$로 볼 수 있다. 이 때, 가운데 그림과 같이 reward의 분포가 초록색 영역은 +1, 나머지 붉은색 영역은 -1로 형성되어 있다면, parameter $\theta$는 분포 $\pi_\theta(s,a)$가 초록색 화살표의 방향으로 이동할 수 있도록 update된다. 그 결과, 평균적으로 높은 reward를 얻을 수 있도록 오른쪽 그림과 같은 $\pi_\theta(s,a)$가 형성되며, 이것이 policy gradient가 올바르게 update되는 원리라고 볼 수 있다.

Policy Gradient Theorem

하지만 사실 위 유도과정엔 논리적 비약이 존재한다. 그 이유는, 바로 stationary distribution $d(s)$의 분포가 policy를 구성하는 parameter $\theta$와 independent하지 않기 때문이다. 따라서 $\theta$에 대한 gradient 연산자가 곧바로 log probability 항에 씌워져서는 안된다.

다행히도 아래의 Policy Gradient Theorem에 의해, 위 유도과정은 모든 objective function에 대해 성립하며, 자세한 증명은 생략하도록 하겠다.

Policy Gradient Theorem
For any differentiable policy $\pi_\theta(s,a)$, for any of the policy objective functions $J=J_1, J_{avR}, \text{ or }\frac{1}{1-\gamma}J_{avV}$, the policy gradient is,

$\nabla_\theta J(\theta) =E_{\pi_\theta}[\nabla_\theta \text{ }log\pi_\theta(s,a)\text{ }Q^{\pi_\theta}(s,a)]$

Stochastic Policy

한편, 위 gradient 값으로 학습될 policy approximator에는 출력값의 조건에 대한 inference가 주어져야 한다. 예를 들어, gridworld에서는 (up, down, left, right, stay) action set에 대한 확률값이 총합이 1이 되도록 출력되어야 하며, input으로 [0, 100]의 입력값을 받는 robot controller의 경우 해당 범위 내의 scalar 값이 올바르게 출력되어야 할 것이다.

이를 위해, Sigmoid 함수와 Softmax 함수를 각각 아래와 같은 상황에 적용할 수 있다.

• 각 state에서 가능한 action이 두 가지인 discrete action space나 continuous action space의 경우
  : Sigmoid 함수($\sigma(t)={\frac {1}{1+e^{-t}}}$)를 이용한다.
  *Action이 두 가지인 경우, sigmoid의 [0, 1] 범위를 갖는 함수값이 한 action을 택할 확률값에 해당하며, 앞선 robot controller의 경우, 출력값을 100만큼 scaling하면 된다.

• 각 state에서 가능한 action이 세 가지 이상인 discrete action space의 경우
  : Softmax 함수($p_j=\frac{e^{z_j}}{\sum_{k=1}^Ke^{z_j}}$)를 이용한다.
  *이를 통해 총합이 1인 유효한 확률값을 얻어낼 수 있다.

Monte-Carlo Policy Gradient : REINFORCE

하지만 policy-based 방식은 value function과 이를 통한 action의 선택과정을 policy에 대한 estimation을 통해 일괄적으로 수행하므로 Policy Gradient Theorem의 $Q^{\pi_\theta}(s,a)$에 대입할 value function 값을 별도로 구해줄 필요가 있다.

이 때, MC에서와 같이, 현재의 policy estimator에 따라 episode를 sampling한 뒤, 지나온 state에 대한 return 값을 계산해 대입할 수 있으며, 이러한 방법을 해당 모델의 논문에서 칭한 대로 'REINFORCE'라 하겠다. 이를 수식으로 나타내면 아래와 같다.

Time-step $t$로부터의 reward에 해당하는 $v_t$는 $Q^{\pi_\theta}(s,a)$에 대한 unbiased sample이라고 볼 수 있기에 사용 가능한 것이다. 이는 MC의 낮은 bias와 높은 variance의 특징을 그대로 물려받게 된다.

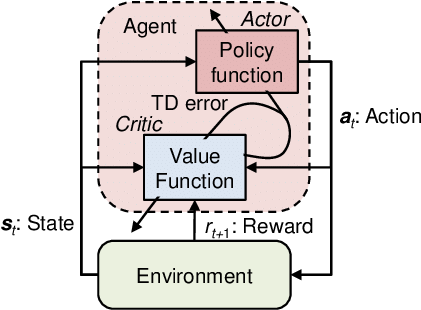
Actor-Critic Policy Gradient

앞선 REINFORCE algorithm은 sampled return 값을 사용하기 때문에 MC의 높은 variance를 보인다는 문제점이 있다. 이에, 현재 필요한 Q-value function도 sampling으로 얻어내지 않고, 새로운 function으로 approximate하여 time-step마다 parameter update를 수행할 수 있도록 하는 방식이 actor-critic policy gradient이다.

따라서 actor-critic algorithm은 아래와 같이 두 가지 parameter를 각각 update하는 부분으로 나누어볼 수 있다.

• Critic : Q-value function을 approximate하는 $w$를 update한다.
• Actor : Critic이 제시한 방향에 따라, policy를 approximate하는 $\theta$를 update한다.

이를 수식으로 나타내면 아래와 같다.

위와 같이 각각 Q-value function과 policy를 approximate하는 $w$, $\theta$는 각 time-step마다 TD(0)의 방식으로 동시에 update해주면 된다. 이전 글에서 다룬 TD(0)에 대한 gradient descent 식에 위 function approximator를 대입하면 아래와 같다.

이처럼, actor-critic algorithm은 policy gradient에서 필요한 value function을 approximator를 통해 time-step마다 계산할 수 있도록 함으로써 학습의 variance를 낮출 수 있다.

비교하자면 Q-learning과 SARSA는 value function만을 학습하고, policy gradient는 policy만을, actor-critic method는 둘을 동시에 학습하는 것이다.

Baseline :: Advantage Function

한편, 학습의 variance를 낮추는 또 다른 방법으로 baseline을 활용할 수 있다. Episode sample를 사용하며 sampling된 state에 대한 dependency가 높아져 variance가 증가한 것이므로, 현재 state에서 action과 무관한 기준치(baseline)를 설정하여 그로부터의 차이만을 parameter update에 반영하는 것이다. 이에, baseline function을 $B(s)$라 하면, 아래와 같은 식이 성립한다. (단, 언급했듯 action $a$와 independent하다는 전제가 주어져야 한다.)

위처럼, objective function의 gradient 식에 baseline function을 대입하면 action에 independent한 성질에 의해 기댓값이 0이 된다. 따라서, 특정 gradient 식의 target value에서 baseline을 빼주어도 그 기댓값은 변하지 않으며, variance 값만 감소시켜줄 수 있는 것이다.

State-value function은 훌륭한 baseline function이 될 수 있다. 이에, policy gradient의 Q-value function에서 state-value function을 뺀 함수를 아래와 같이 advantage function $A^{\pi_\theta}(s,a)$라고 정의할 수 있다.

이를 policy gradient 식에 대입하면 아래와 같다.

하지만, 위와 같이 advantage function을 사용하기 위해서는 아래와 같이 각각 state-value function과 Q-value function을 estimate하는 두 개의 approximator를 사용해야 한다.

이는 critic에서 학습시켜야 하는 parameter가 $w$와 $v$ 두 가지가 되어 inefficient하다. 하지만 Q-value function이 immidiate reward와 state-value function의 합이라는 관계를 이용하면 아래와 같이 advantage funtion에 대한 unbiased estimate을 state-value function으로만 구성된 TD error $\delta^{\pi_\theta}$로 표현할 수 있다.

따라서 policy gradient 식에 TD error를 대입하면 아래와 같다.

앞서 critic에서 정의한 Q-value function approximator $Q_w(s,a)$와 같이, 위 식에서의 TD error 값을 estimate하는 approximator $\delta_v$를 정의할 수 있다.

Actor-critic algorithm에선 parameter $\theta$와 Q-value function을 approximate하는 $w$를 동시에 학습시켰다면, advantage function을 이용하는 경우 parameter $\theta$와 state-value를 approximate하는 $v$를 동시에 학습시켜주면 된다.

한편, 앞서 TD($\gamma$)를 통해 TD(0)의 높은 bias를 낮춰주었듯이, 위 policy gradient에도 $\gamma$-return 값을 사용해 bias 값을 조절할 수 있다.

지금까지 7편의 글을 통해 reinforcement learning의 기초적인 내용을 살펴보았다. 개념의 흐름을 간단히 요약하면 아래와 같다.

1. MDP에서 정의되는 Value Function과 그들의 관계식인 Bellman Equation
2. Planning에 해당하는 DP (Policy Iteration/Value Iteration)
3. Learning에 해당하는 MC와 TD (SARSA)
4. Behavior policy를 분리한 Off-Policy Control (Imporatnce Sampling/Q-Learning)
5. Tabular 방식을 벗어난 Value Function Approximation과 Deep Q-Networks
6. Policy만을 estimate하는 Policy Gradient와 value function도 함께 estimate하는 REINFORCE/Actor-Critic

---

References

• UCL Course on RL, David Silver
• Reinforcement Learning: An Introduction, Richard S. Sutton
• Fundamental of Reinforcement Learning, 이웅원
• Deep Reinforcement Learning: Pong from Pixels, Andrej Karpathy