지난 Euron 동아리 활동에서 Transformer가 과연 시계열 특성을 갖지 않는 image에 대해서 얼마나 효용성이 있을지에 관해 의논했다. VATT 논문이 Transformer 구조를 이용해 Multi-modal task를 수행하는 model을 만들고자 하며 맥락을 갖는 특성이 있다는 이유로 학습 데이터의 type을 video로 사용했다는 부분에 대해서 의문을 갖고 시작한 논의였다. 그에 관해 일부 답을 얻을 수 있는 논문으로 제시된 "Are Transformers Effective for Time Series Forecasting?"을 이번에 리뷰해보려고 한다.
(참고한 링크
https://velog.io/@ha_yoonji99/%EB%85%BC%EB%AC%B8%EB%A6%AC%EB%B7%B0-Are-Transformers-Effective-for-Time-Series-Forecasting-AAAI-2023-NLinear-DLinear
https://today-1.tistory.com/60
https://data-newbie.tistory.com/944
https://seollane22.tistory.com/23
https://dacon.io/forum/401774
Intro
이론적 배경
Transformer 구조
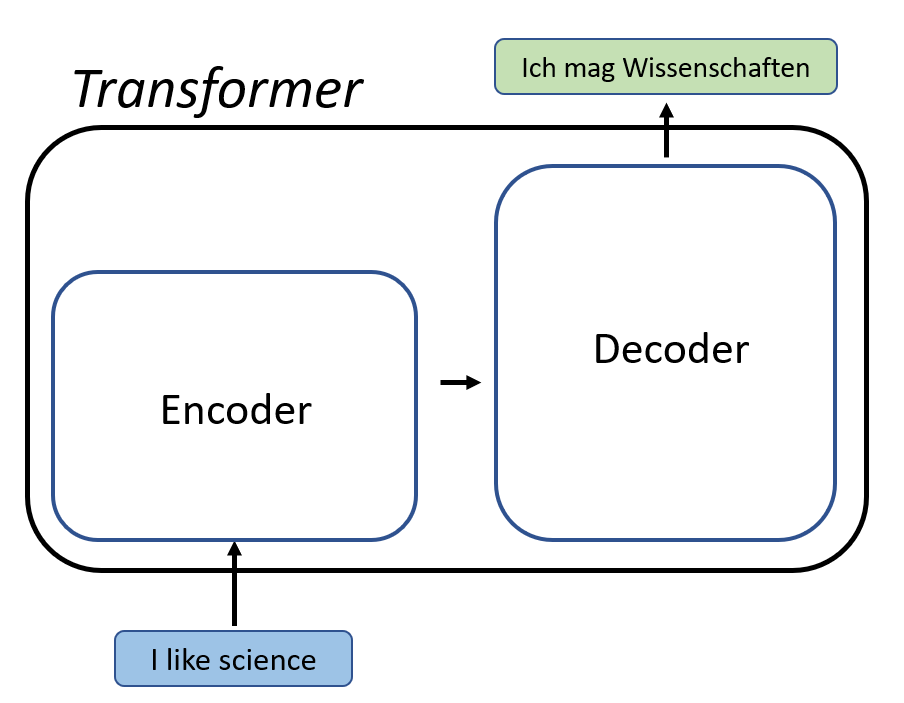아주 간단하게 표현한 Transformer 구조이다. 이는 self-attention이라는 특수한 구조를 활용하는데 이런 특성이 Transformer model이 sequential data를 다루는 task에 능하게 해준다. Transformer는 Encoder와 Decoder로 이루어져 있는데 변형된 Transformer 구조들 중에서는 둘 중 하나만 있는 경우도 많다. 주로 맥락 정보를 담고 있는 task에 강점을 보이는데 이 때문에 NLP에서 각광받고 있다. NLP에서 유명한 BERT는 Transformer의 encoder 구조를 응용해서 변형한 언어 인식 모델이고, 최근 Generative AI로 가장 주목받은 ChatGPT는 Transformer의 decoder 구조를 응용해서 변형한 언어 생성 모델이다.
Long Term Time Series Forecasting
긴 시간 동안의 series에 대해서 예측하는 task를 LTSF라고 줄여 부른다. 이 task는 주기성과 추세를 갖는 시계열 데이터에 대해서 다음 추세를 예측하는 task를 지칭하는 경우가 많다.
과연 Transformer가 LTSF에 대해서 강점이 있는가?
Transformer에서 가장 특징적인 부분은 self-attention 구조이다. 이 구조는 순서대로 들어온 정보에 대해서 앞뒤 내용의 맥락 정보를 인지하는 것에 강점을 갖고 있는데 이 논문에서는 이것이 과연 LSTF task에도 유용한지 의문을 던지고 있다. 특히 시계열 데이터는 time order에 대한 정보가 중요하게 작용할텐데 Transformer의 self-attention 구조는 그 order 정보를 누락시킬 수 있기 때문에 시계열 정보를 다루는데 있어서 한계가 있지 않느냐는 의견이 있었다. 게다가 look-back window sizes를 증가시켜도 예측 오류가 감소하지 않는 현상으로 인해 Transformer가 시간 순에 대한 관계 특성을 추출하지 못한다는 것을 발견한 예도 있다.
Transformer for LTSF
Preliminaries: TSF Problem Formulation
Iterated Multi-Step forcasting(IMS)과 Direct Multi-Step forcasting(DMS)을 비교하고 있다. 단순히 요약하자면, DMS가 LTSF에서 더 긴 시계열을 다룰 수록 유리하다. IMS는 one step 시계열 예측 모델을 이용해서 여러 time step의 내용을 예측하는 방식이고, DMS는 예측하고자 하는 하나의 time step마다 별개의 모델을 생성하는 방식이다. 어쩌면 자명하게 time step이 길어질 수록 IMS는 error가 누적될 것이므로 DMS에 비해 성능이 낮은 것은 당연하다.
Transformer-Based LTSF Solutions
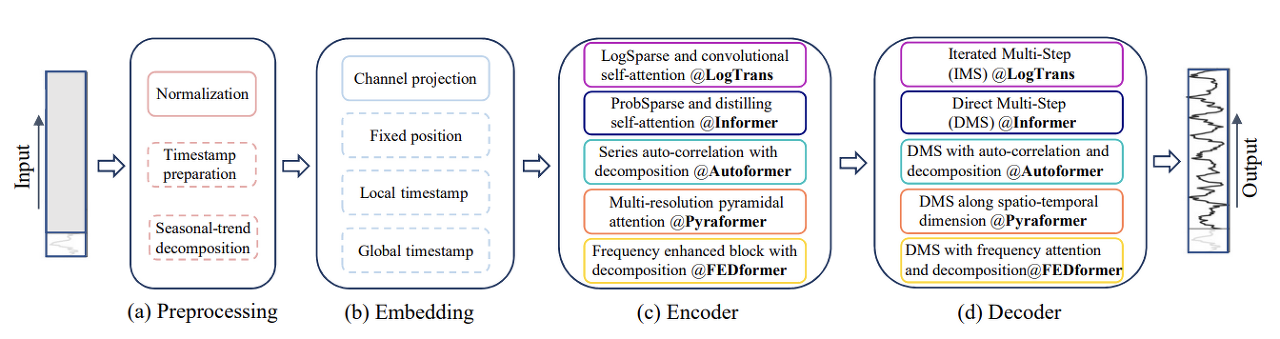이는 Transformer 구조를 기반으로 한 LTSF 문제를 해결하고자 하는 시도이다. Transformer는 self-attention을 통해 장기적인 시계열 문제에 대해서 적절히 과거 정보를 누락하여 가까운 거리 내의 맥락을 파악하는 것에 강점을 갖고 있었다면 장기적으로 order에 대한 정보와 그 사이의 의존성을 추출해야 하는 LTSF 시계열 문제를 해결하기 위해서는 그러한 transformer의 특성을 조절할 필요성이 있었다. 여러 연구적 시도들이 Transformer의 LTSF 문제 해결 능력을 증대시키기 위해서 노력을 해왔고 그 중에서는 vanilla Transformer가 LTSF task를 효과적으로 수행할 수 있도록 한 것도 있었다.
Time Series Decomposition
보통 TSF task를 위한 model을 normalization을 하기 위해서는 zero-mean을 data preprocessing에 사용한다. 그에 비해 Autoformer는 seasonal-trend decomposition을 적용했다. 시계열 요소 분해는 시계열 분석에 있어서 표준 방식인데 시계열이 갖는 변동성을 분해하여 복잡한 변동성의 요인들을 알아볼 수 있도록 하는 것이다. Autoformer는 seasonal-trend decomposition block을 모듈 내부에 배치한 것은 시계열의 세부적인 변동성을 더 깊게 파악할 수 있도록 해주었다.
Time Series Decomposition을 적용하는 연구에는 moving average kernel을 통해 순환하는 변동성을 추출하고자 했고, 이를 통해 seasonal trend를 얻었다.
Input embedding strategies
self-attention layer는 input series의 positional information 즉 order 정보를 고려하지 않고 전체 데이터를 사용한다. 그러나 시계열 데이터는 각각의 local positional information이 매우 중요하기 때문에 예측을 적용할 때 time step의 local position을 고려해야 한다. 여기서 hierachicla time stamps와 agnostic timestamps 같은 global info 또한 분석에 사용해야 한다.
그래서 이런 location info를 transformer model 내에서 보존하기 위해 input embedding에 있어 여러 방법론이 제시되었고, 그 중 고정된 position info를 넣어주는 fixed positional encoding과 channel projection 등이 있다. 그 외에도 학습 가능한 temporal embedding을 input sequence에 적용하거나 CNN layer를 배치하는 등의 방식도 있다.
Self-attention Schemes
transformer의 self-attention은 sequential data 사이의 sementic dependency를 추출하는 기능을 한다. 이 방식은 input sequence 길이의 2배 수준의 complexity를 갖는 부작용이 있다. 이를 해결하고자 quadratic complexity를 해소하고 효율성을 개선하고자 하는 연구가 있어 왔다.
1. Introduce Sparsity Bias
2. Introduce the low-rank property
Decoders
vanilla transformer의 decoder는 layers를 지나서 autoregressive한 방식으로 output 값을 하나 씩 출력한다. 이러한 IMS 방식은 오류가 축적되고 속도도 느려지는 문제가 있다. 그래서 Decoder의 구조를 변형하여 IMS가 아닌 DMS 방식으로 LSTF task를 다루도록 한 것들이 있다.
그러나 위와 같은 연구에도 불구하고 transformer의 sementic dependency를 추출하는 특성은 시계열 데이터를 다루는 것에 분명한 한계가 있고 input sequence와 함께 넣어주는 positional information에만 의존하기 때문에 general하지 않다는 문제도 있었다.
An Embarassingly Simple Baseline
논문의 저자들은 그들의 주장대로 transformer가 더이상 LTSF에 강하지 않을 수 있다는 것을 증명하기 위해서 위와 같은 단순한 DMS model baseline을 제시하였다.
성능 비교를 위해 제시된 모델은 다음과 같다.
(출처: https://seollane22.tistory.com/23)
-
DLinear
이 모델은 Decomposition을 이용한다. Decomposition의 매커니즘은 autoformer에서 제안된 것과 같은데, 먼저 raw 데이터를 요소분해를 통해 trend와 reminder(seasonal) 변동으로 분리한다. 이후 각 요소에 레이어를 하나씩 배치하여 각 변동을 따로 학습한 뒤 마지막에 그 결과를 합친다. 이것은 분명한 트렌드가 있을 때 그 성능을 강화할 수 있도록 설계한 것이다. -
NLinear
이 모델은 인풋 시리즈를 그 인풋의 마지막 값으로 모두 빼준다. 그렇게 일종의 차분을 진행한 후 레이어를 통과시키며 마지막 최종 예측단계에서 다시 마지막 값으로 더해주어 아웃풋을 완성한다. 이러한 과정은 인풋 시리즈/시퀀스에 대한 간단한 표준화(정규화)이며, 이는 인풋이 데이터 셋 안에서 분포가 급격하게 변하는 지점에 잘 적합하도록 하기 위함이다.
Experiments
Transformer와의 비교
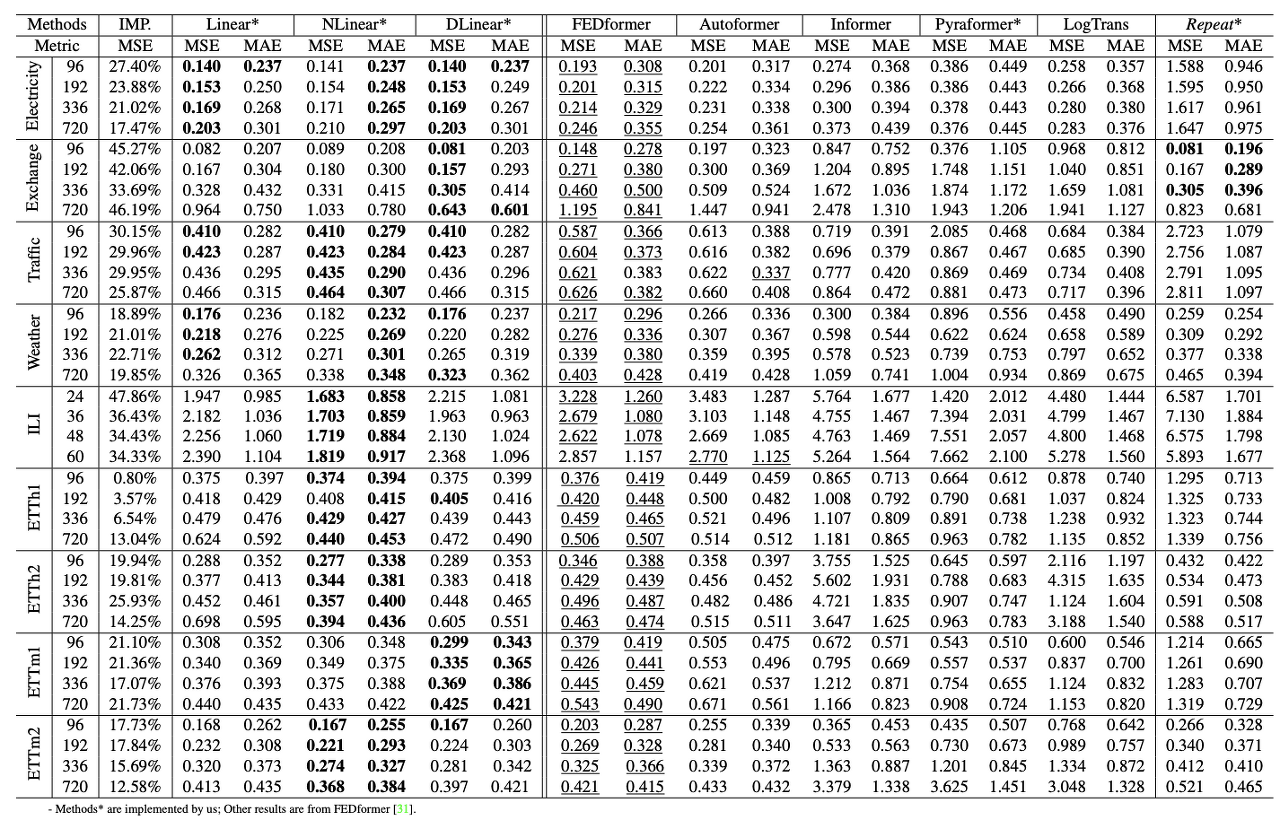다변량 예측 실험에 대해서 L-Linear 모델이 FED-former보다 더 좋은 성능을 보이고 있었다. 거의 대부분의 상황에서 훨씬 높은 성능을 보인다는 점에서 transformer보다 훨씬 단순한 형태의 linear based model이 더 시계열 데이터를 잘 다룰 수 있다는 결론을 내릴 수 있었다.
More Analyses on LTSF-Transformer
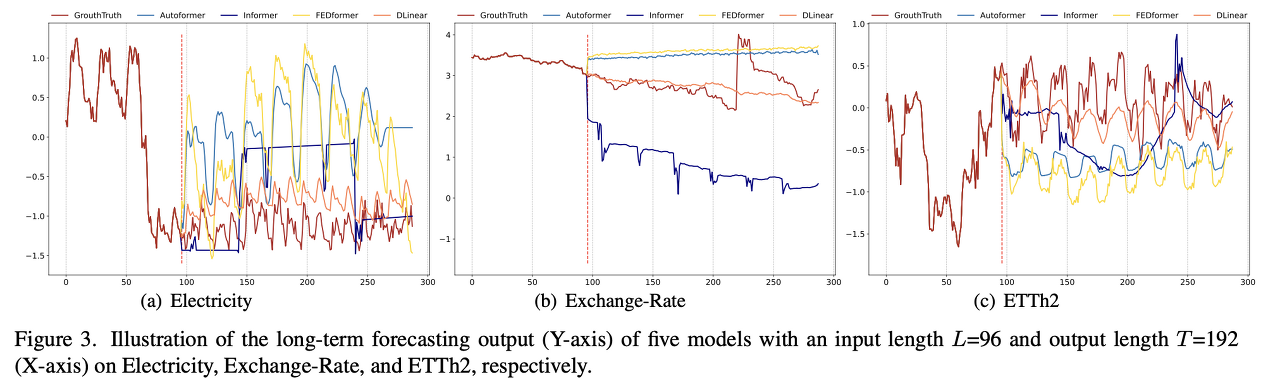
Can existing LTSF-Transformer extract temporal relations well from longer input sequences?
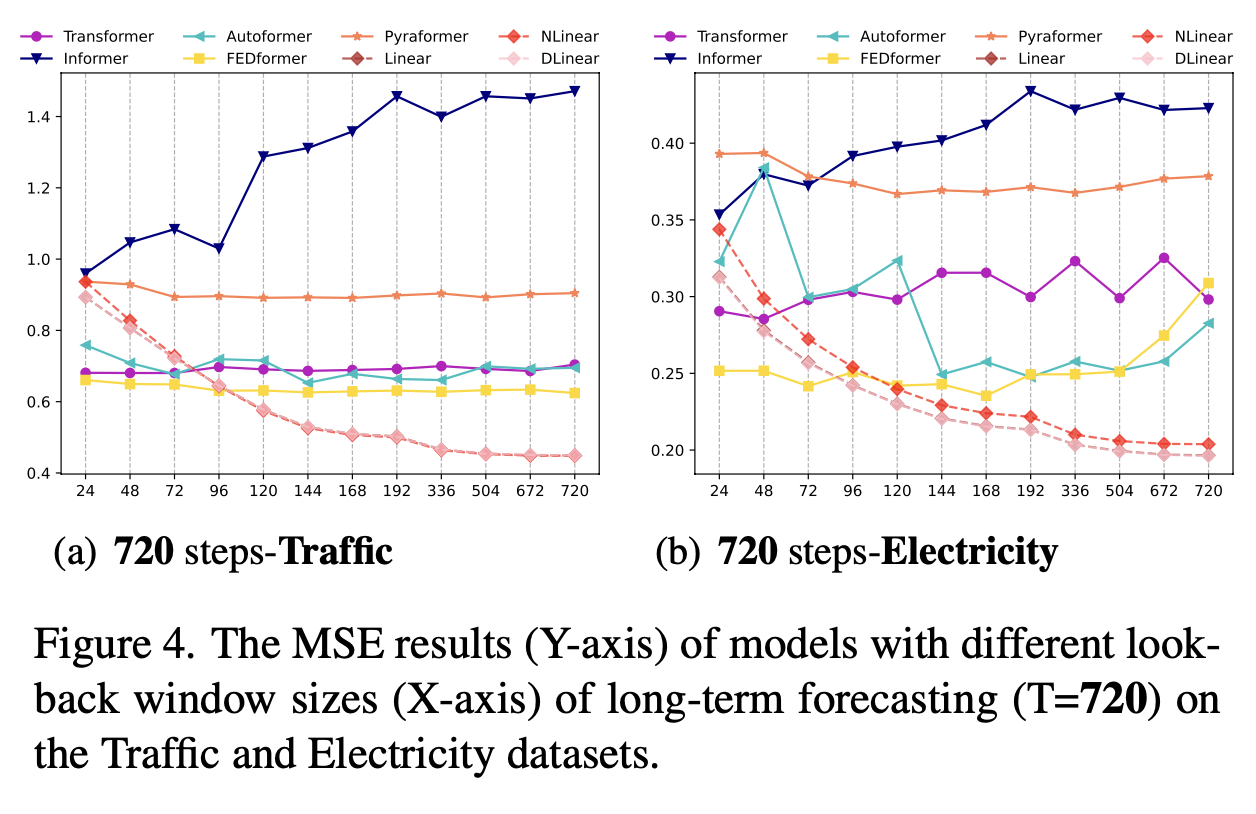
What can be learned for long-term forecasting?
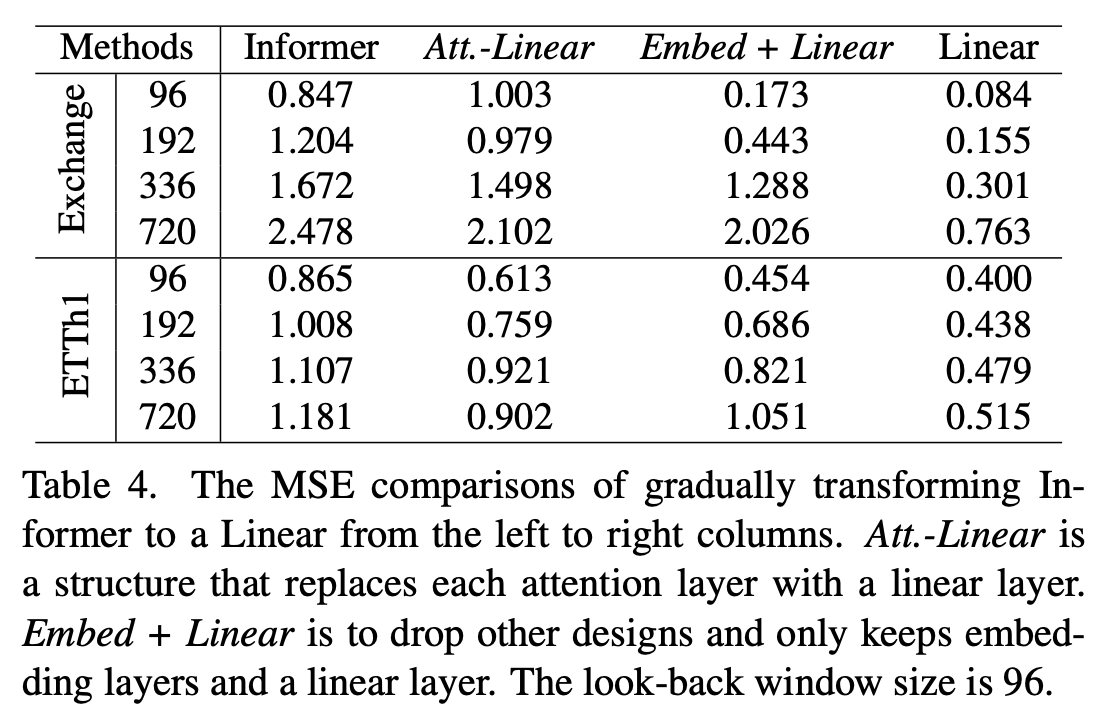
Are the self-attention scheme effective for LTSF?
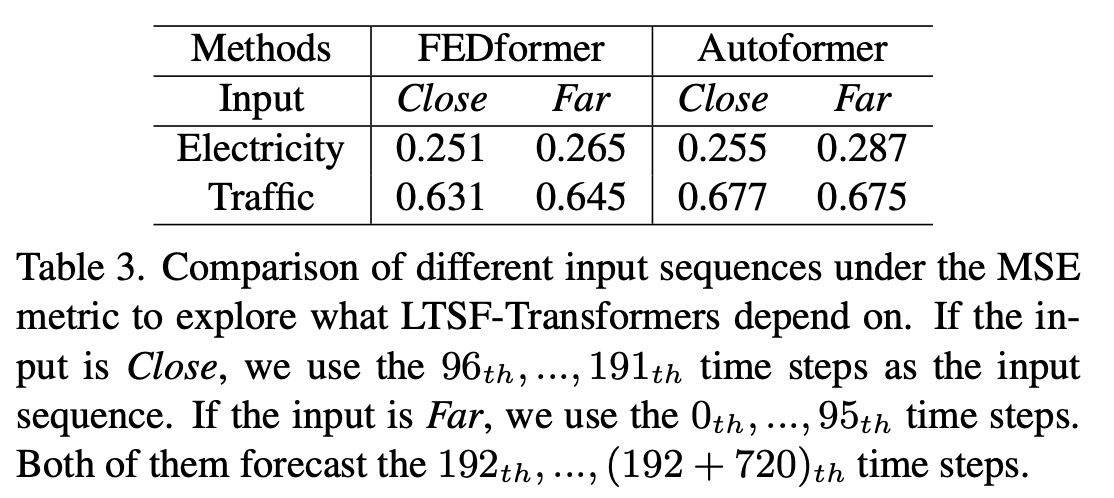
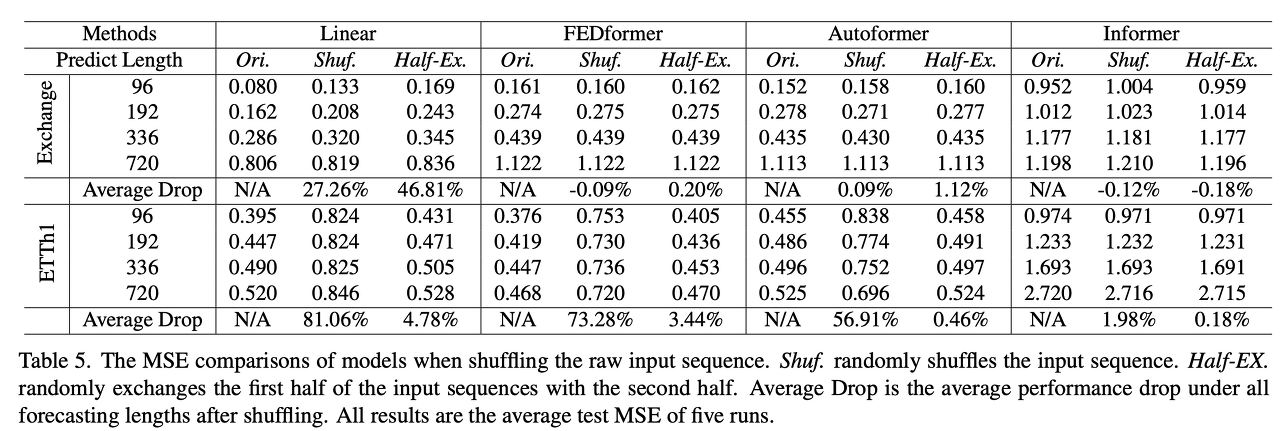
Can existing LTSF-Transformer preserve temporal order well?
Have effective are different embedding strategies?
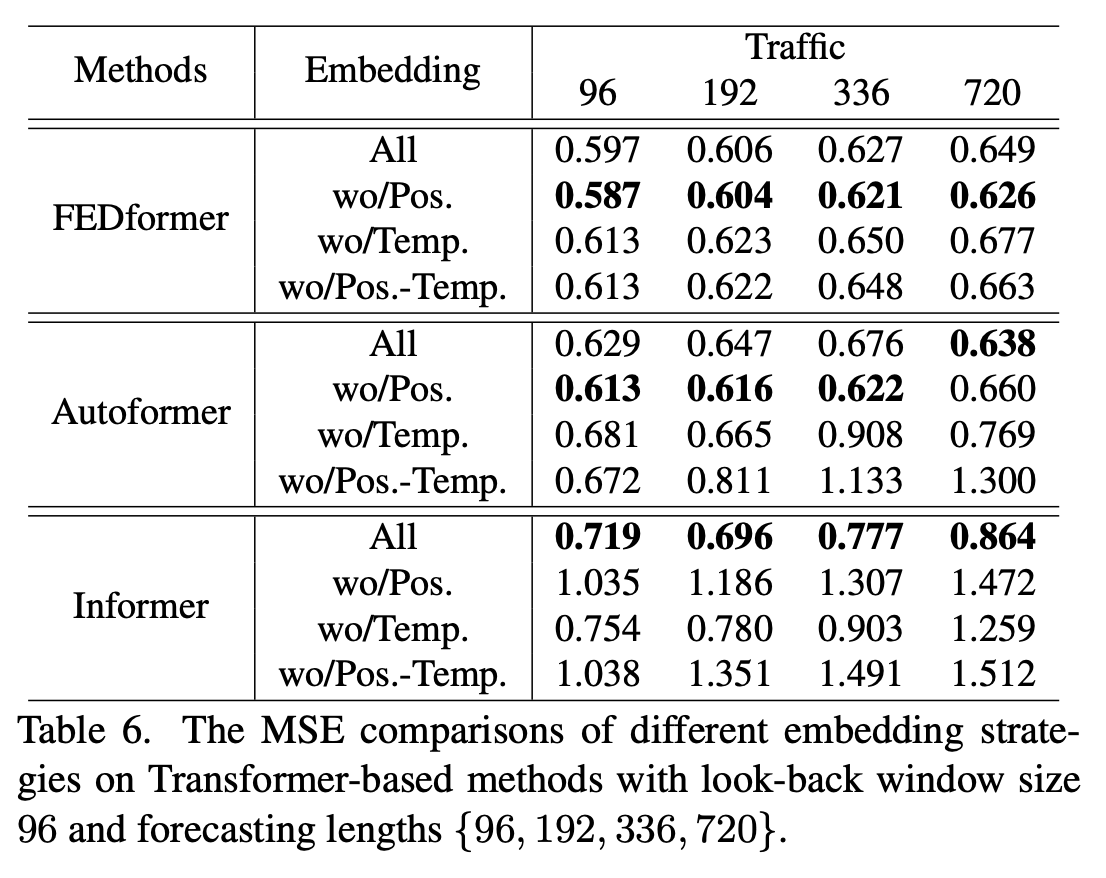
Is training data size a limiting factor for existing LTSF-Transformer?
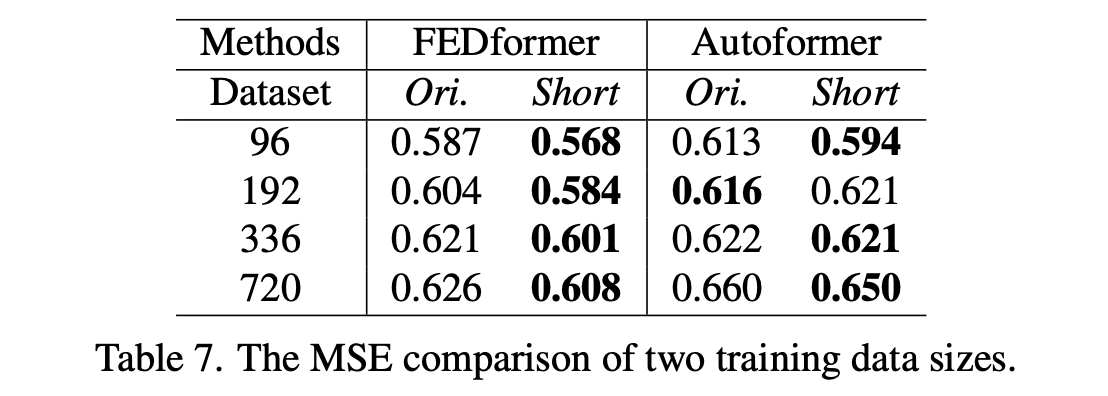
Is efficieny really a top-level priority?
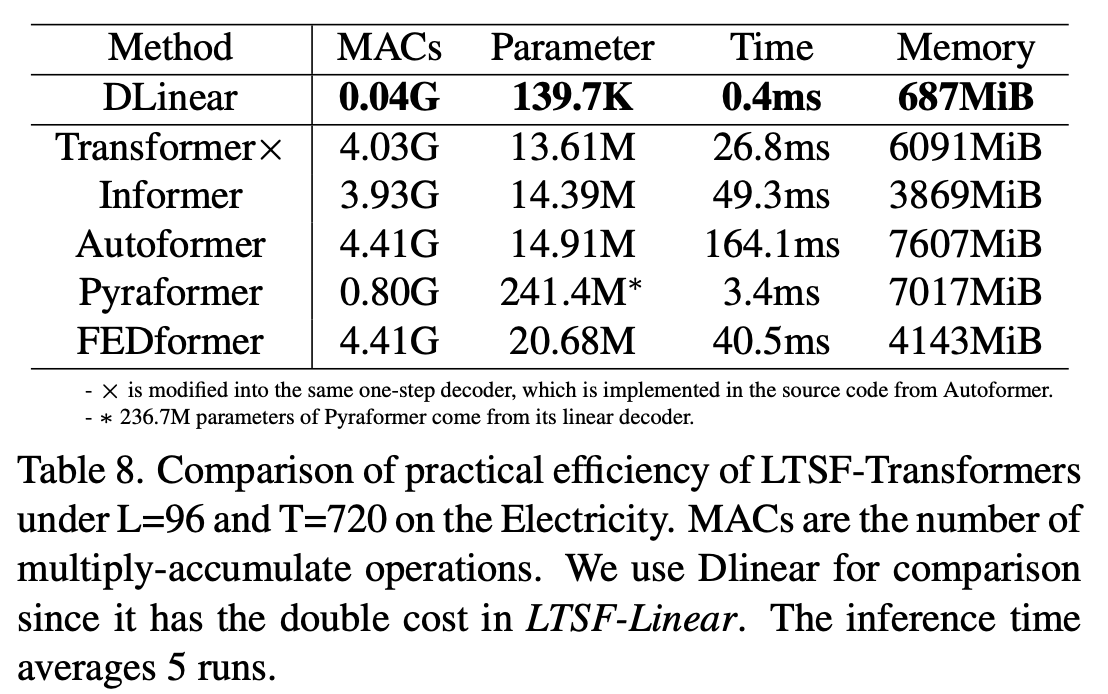
Conclusion
(추가 예정)
