TIL(20.03.24) Immersive # 7 Time complexity

Time complexity (시간 복잡도)

What is Time complexity?

시간 복잡도는 알고리즘을 실행하는 데 걸리는 시간을 설명하는 계산 복잡도입니다. 시간 복잡도는 일반적으로 알고리즘에 의해 수행되는 기본 동작의 수를 세어, 각 기본 동작에 일정한 시간이 걸린다고 가정을 함으로서 추정을 합니다. 시간 복잡도와 더불어 공간 복잡도라는 개념이 있습니다.

공간복잡도는 알고리즘의 공간(메모리) 효율성을 의미합니다.

시간 복잡도의 표기법으로는 Big-O(빅-오),big-Ω(빅-오메가),big-Θ(빅-세타) 표기법이 있습니다.

시간 복잡도의 표기법중에 빅오 표기법을 대표적으로 사용합니다. 세가지 표기법에서 빅오 표기법을 가장 많이 사용하는 이유는 빅-오 표기법의 개념에 있습니다.

빅-오메가 표기법은 하한선을 기준으로 하고 빅-세타 표기법은 상한선과 하한선 사이를 기준으로 합니다. 빅오 표기법은 상한선을 기준으로 표기를 합니다. 항상 실생활에 있어 최악의 경우를 대비 해야합니다. 빅-오메가 표기법과 빅-세타 표기법은 최악의 경우의 수를 따져 주지 않았고 빅-오 표기법은 최악의 수 까지 따졌기 때문에 시간 복잡도에서 빅-오 표기법이 가장 많이 쓰인다는 것을 알 수 있습니다. 여기서 중요한 것은 빅-오 표기법을 썻다고 해서 상한선 즉 최악의 경우의 수 까지 고려 햇을뿐 빅-오 표기법이 꼭 최악의 경우의 수는 아니라는 것 입니다.

빅-오 표기법 상한선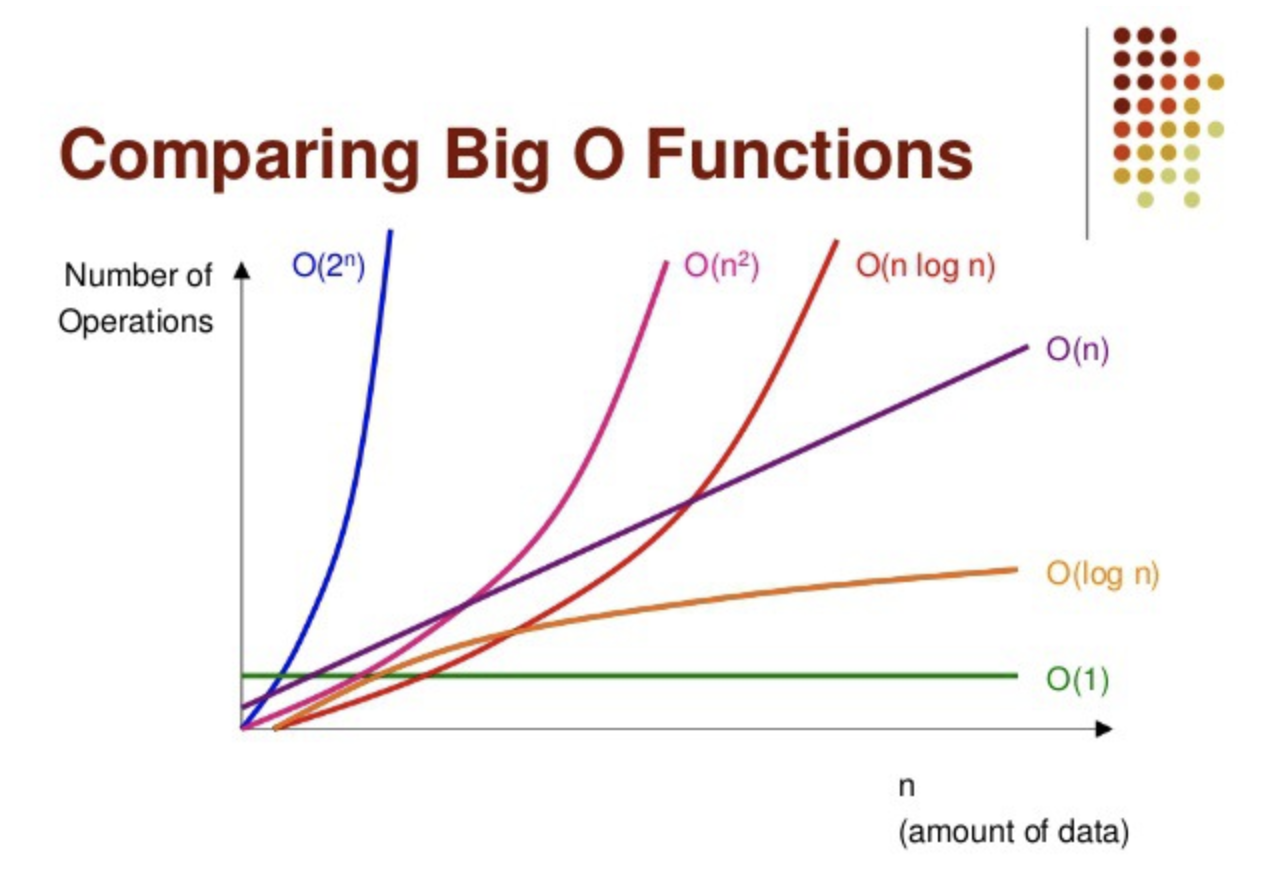

그러면 시간복잡도를 자료구조에 적용을 시켜 자료구조는 어떠한 시간 복잡도를 가지고 있는지 알아 보겠습니다.

자료구조에서의 시간 복잡도

스택

스택의 메소드에 대해 시간 복잡도를 구해 보겠습니다.

Stack Method

• push : 스택의 삽입

• pop : 스택의 삭제

< 스택의 시간 복잡도 >

push : O(1)

스택에 자료를 추가할 때는 항상 스택의 맨위에 자료를 push하기만 하면 된다. 즉 자료의 개수가 몇개인지와 같은 다른 사항을 고려할 필요가 없이 새로운 자료를 기존의 자료 맨위(top)에 올리기만 하면 된다는 뜻입니다

pop : O(1)

삽입과 마찬가지로 자료의 개수에 상관 없이 맨위의 데이터를 제거 해주면 되기 때문에 O(1)로 표기 할 수 있습니다.

Search : O(n)

만약 스택에 5개의 데이터가 쌓여 있다면 내가 원하는 데이터를 찾기 위해서 최악의 경우 맨 위 부터 맨 밑의 데이터까지 검색해야하는 경우가 생깁니다. 이런 경우 스택의 검색 횟수는 O(n)가 됩니다.

큐

Queue Method

• enQueue : 큐의 삽입

• deQueue : 큐의 삭제

Queue time complexity

enQueue : O(1)

큐에서 자료가 삽입 될 때 맨 뒤에 자료가 삽입 되는 연산만 수행 되므로 O(1)로 표기 할 수 있습니다.

deQueue : O(1)

큐에 자료를 삭제 할 때 다른 데이터에 관계 없이 맨 앞의 자료만 제거 해주면 되기 때문에 O(1)으로 표현 할 수 있습니다.

Search: O(n)

큐에서의 원하는 데이터를 검색하기 위해서 큐 내부의 데이터를 순회 하여 찾아야 하기 때문에 O(n)로 찾을 수 있습니다.

단일 연결 리스트

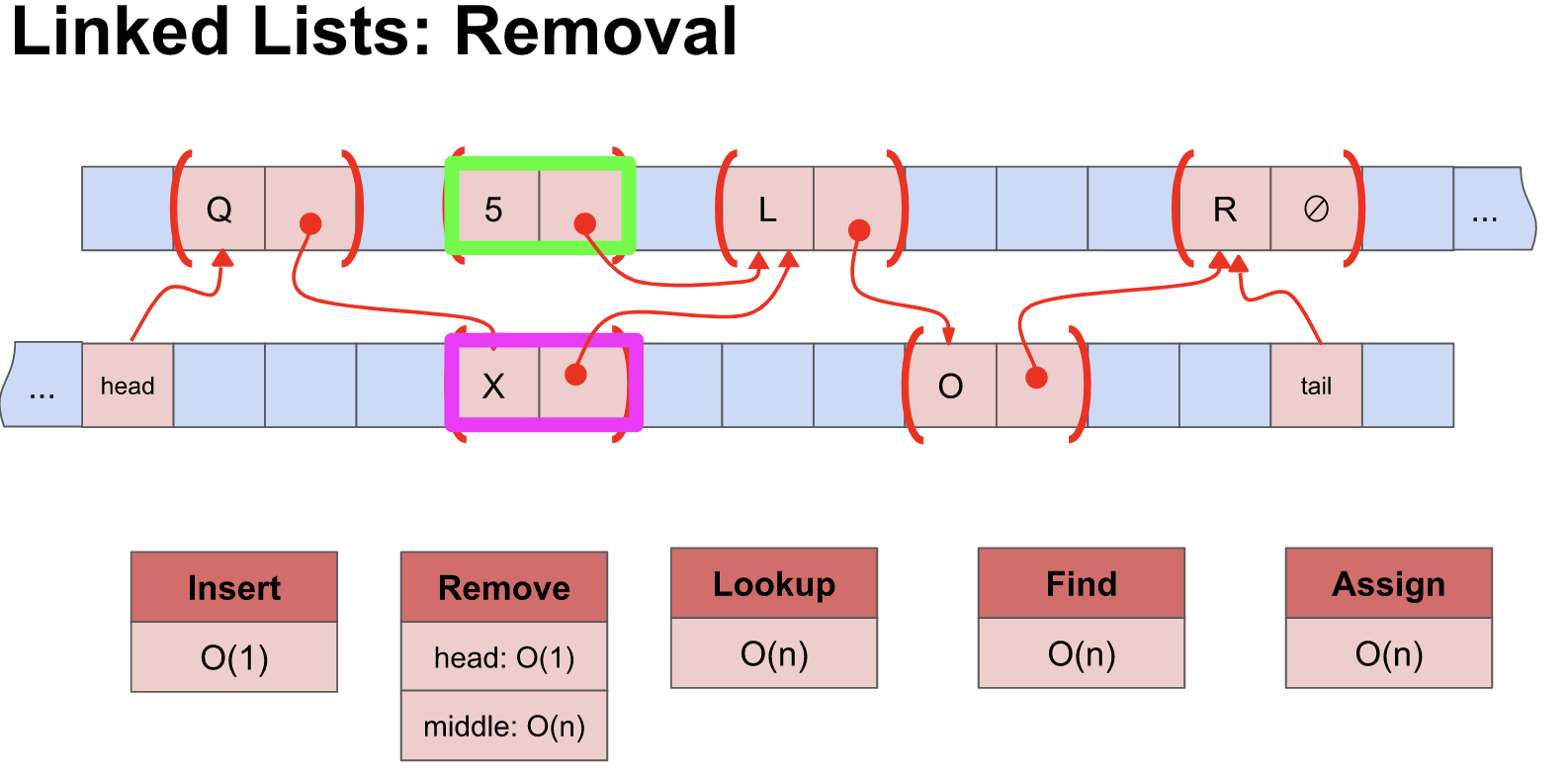
 Insert : O(1)

단일 연결 리스트에서의 삽입은 자료를 추가할 장소로 가서 삽입 이전 노드의 링크를 끊은 다음 추가할 위치의 이전 요소의 링크와 삽입할 자료의 링크를 연결헙니다. 삽입 과정에서 앞 요소와 다음 요소를 연결 시켜주는 operator만 수행 되므로 시간 복잡도는 O(1)라고 할 수 있습니다.

 delete : O(n)

단일 연결리스에서의 삭제는 3가지가 있습니다. 머리 노드 삭제, 꼬리 노드 삭제, 중간 노드의 삭제가 있다. 머리 노드와 꼬리 노드의 삭제는 다른 데이터와 관계없이 앞 노드의 링크와 마지막 노드의 전 노드의 링크를 제거함으로서 삭제가 가능합니다. 여기서 중간 노드의 삭제 같은 경우 노드를 탐색한 후 링크를 제거하는 방식으로 삭제가 이루어 지기 때문에 O(n)로 표현 할 수 있습니다.

assign : O(n)

원하는 노드 배정은 선형 연결리스트를 순회하여 배정 해야하기 때문에 O(n)가 됩니다.

find : O(n)

원하는 노드를 찾기 위해서 assign과 마찬가지로 연결리스트를 순회하여 찾아야 하기 때문에 O(n)가 됩니다.

이중 연결 리스트

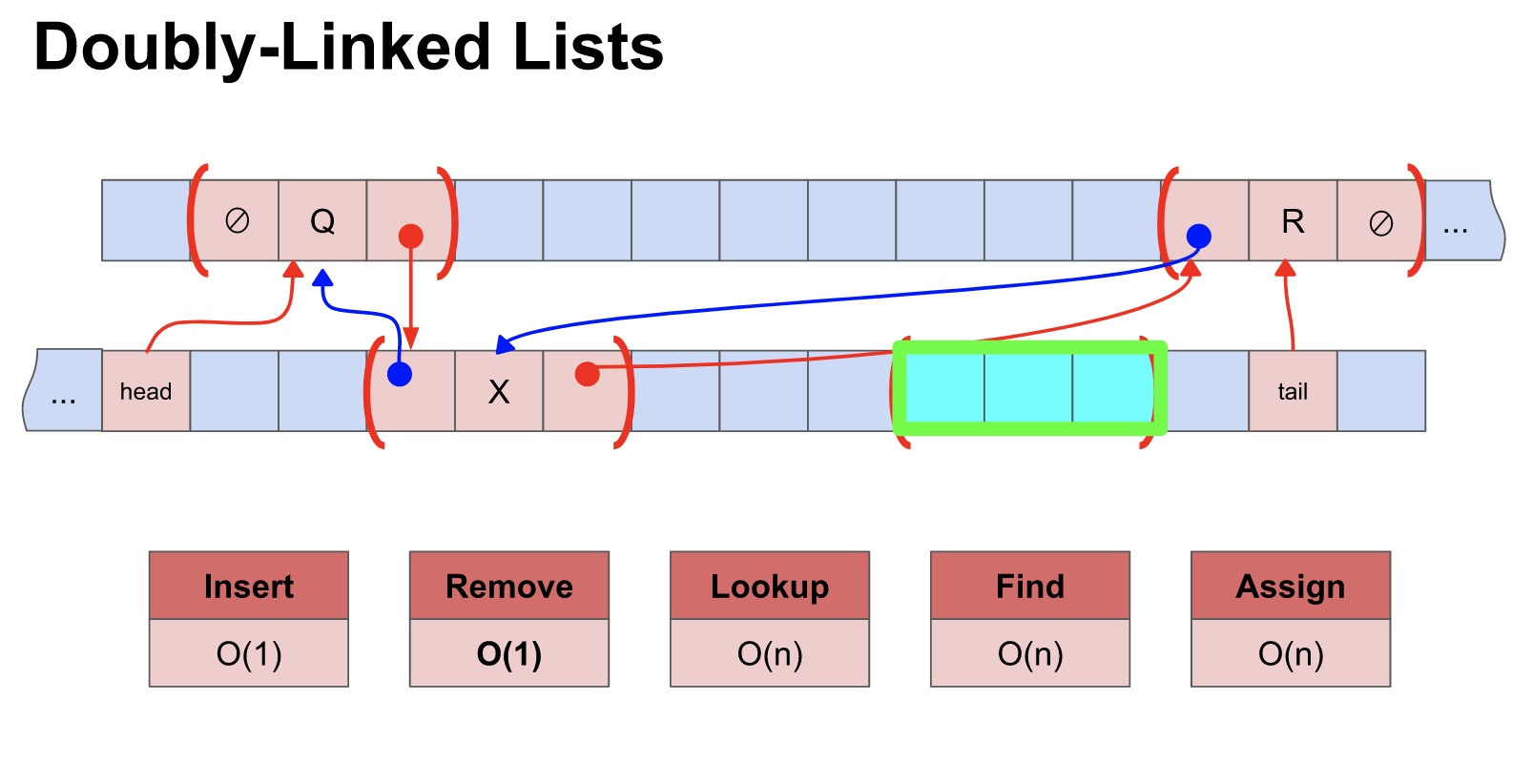
이중 연결리스트 method

이중 연결리스트에서 시간복잡도는 삭제를 제외하고 단일 연결리스트와 동일합니다. 따라서 삭제만 설명하겠습니다.

Insert : O(1)

delete : O(1)

이중 연결 리스트에서의 삭제는 삭제노드의 이전 노드와 다음 노드의 정보를 알고 있기 때문에 데이터 탐색을 할 필요 없이 바로 삭제가 가능 합니다.

assign : O(n)

find : O(n)

이진 검색 트리

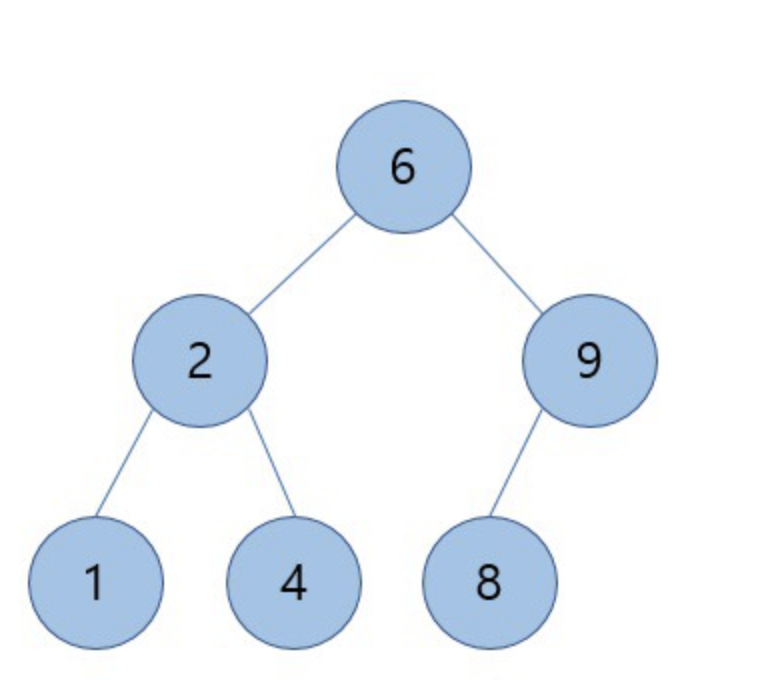
위의 그림은 이진 검색트리의 예시 그림입니다. 그림을 보면 루트노드를 기준으로 왼쪽 노드는 작은 값이 오른쪽 노드는 큰 값으로 구성되어 있는 것을 알 수 있습니다.

< Binary search tree method >

searching : 탐색

Insert : 삽입

Delete : 삭제 

< Binary search tree time complexity >

searching : O(log n)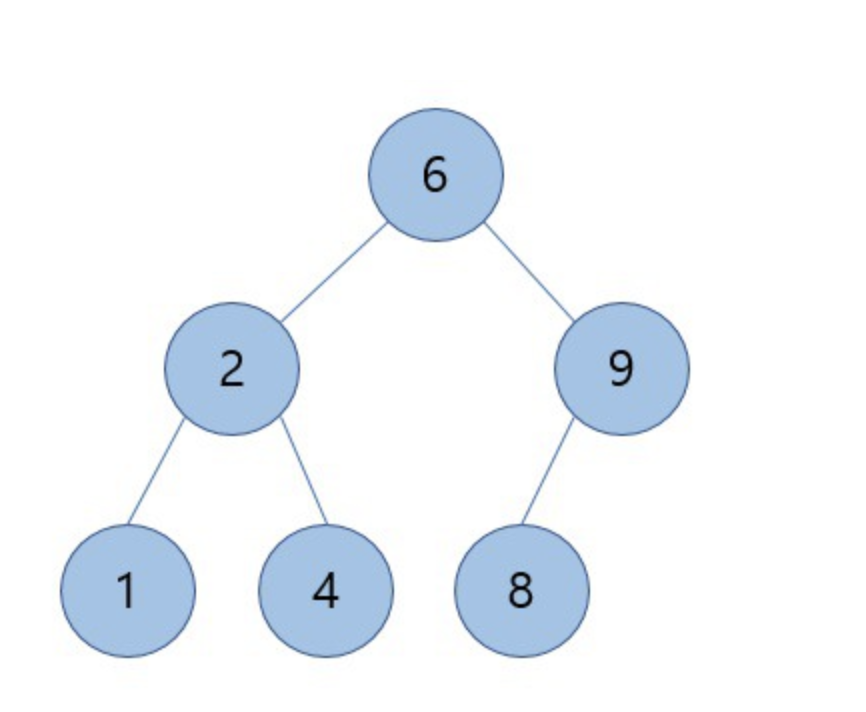

위의 그림을 가지고 탐색을 해보겠습니다.

먼저 루트노드 6과 8을 비교 했을 때 8은 6은 오른쪽 서브트리에 존재하기 때문에 왼쪽 서브트리는 탐색할 필요가 없습니다. 다음으로 오른쪽 서브트리의 루트노드인 9와 8을 비교하면 8은 9보다 작기 때문에 왼쪽 서브트리로 내려갑니다. 9의 왼쪽 서브트리에 우리가 찾고자 하는 8을 찾았습니다.

이진 검색트리에서 탐색 연산의 시간 복잡도는 O(log n)이 됩니다.

Insert : O(log n)

이진 검색트리의 삽입은 탐색을 통해 이루어 지기 때문에 탐색과 같은 시간 복잡도인 O(log n)이 됩니다.

Delete : O(log n)

이진 검색 트리의 시간 복잡도를 구하기 전에 삭제 작동 원리에 대해 알아 보겠습니다.

이진 검색 삭제

1) 삭제하려는 노드의 자식노드가 존재하지 않는 경우

삭제하려는 노드의 자식노드가 존재하지 않는 경우 바로 삭제가 가능합니다.

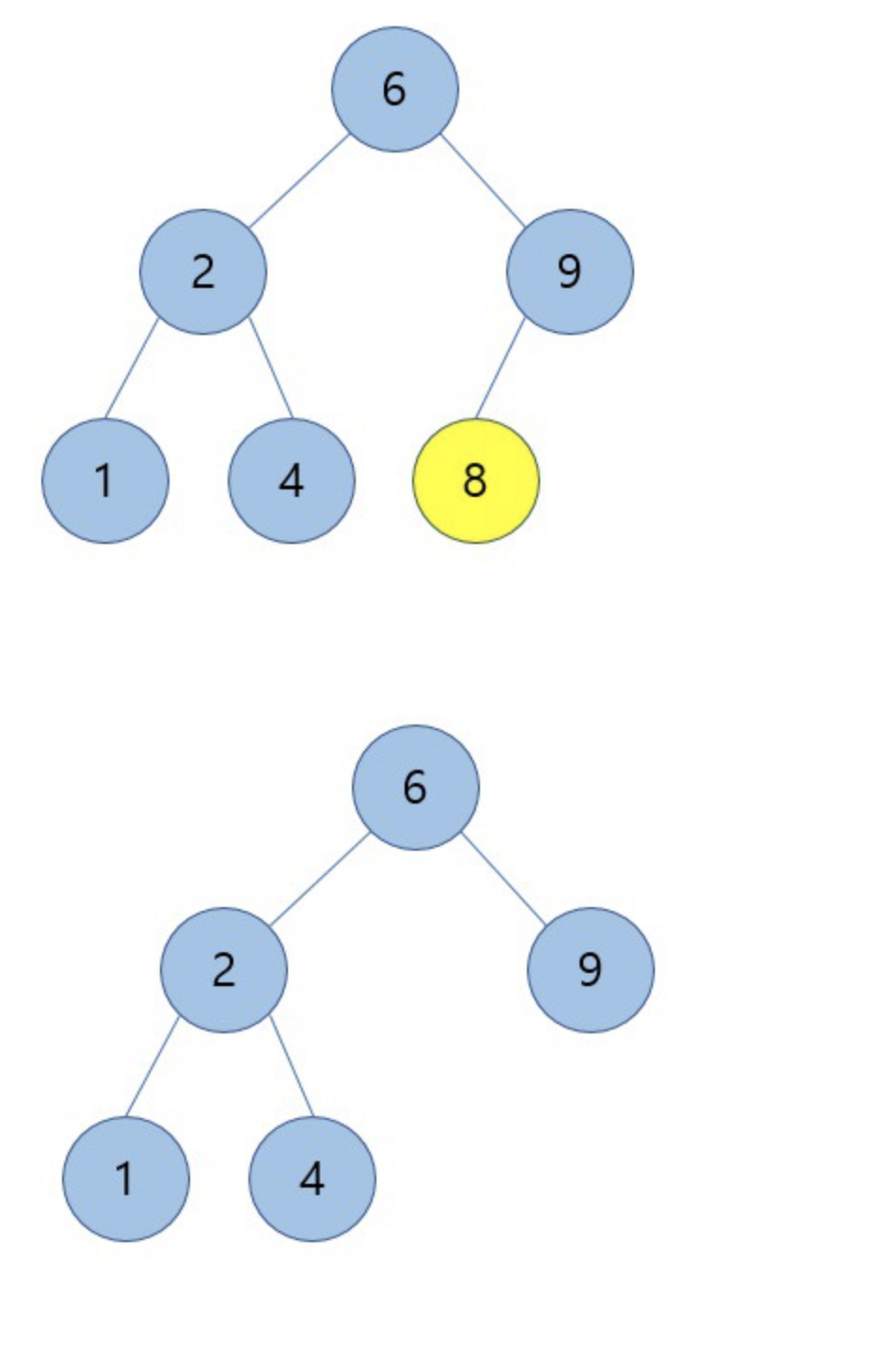
2) 삭제하려는 노드의 자식 노드가 1개만 있는 경우

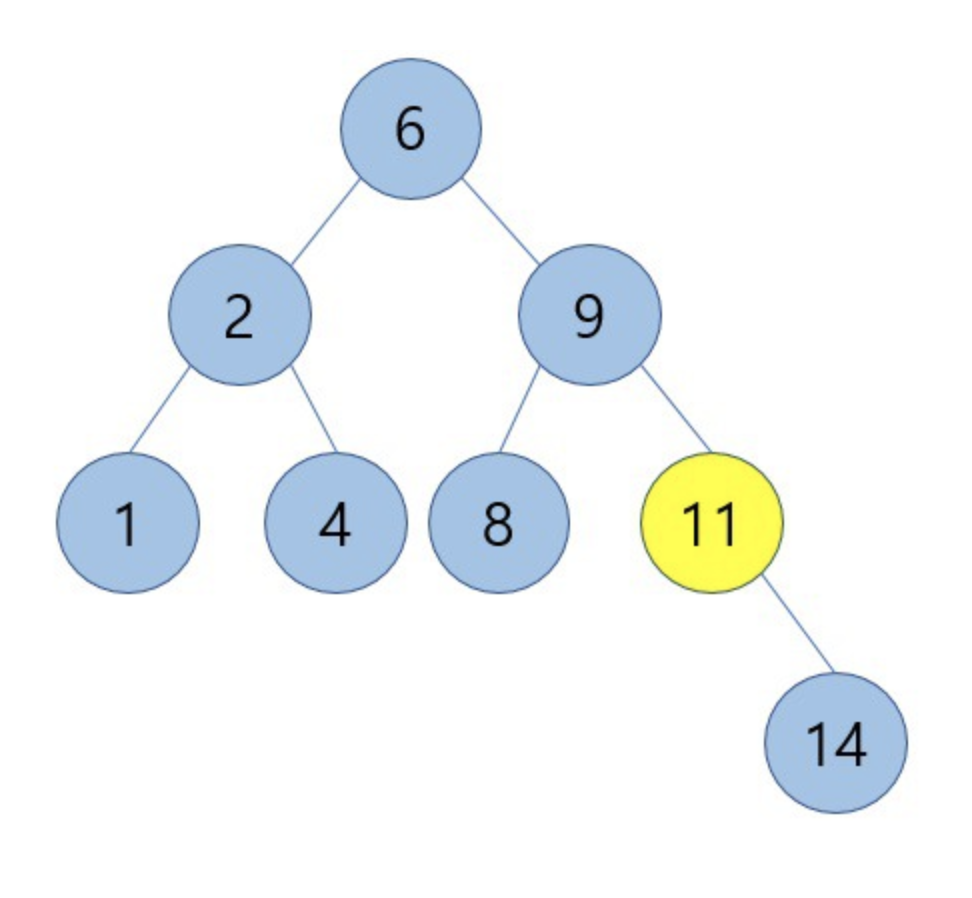
해당 노드를 삭제하고 해당 노드의 자식 노드와 부모 노드를 연결 시켜 줍니다.

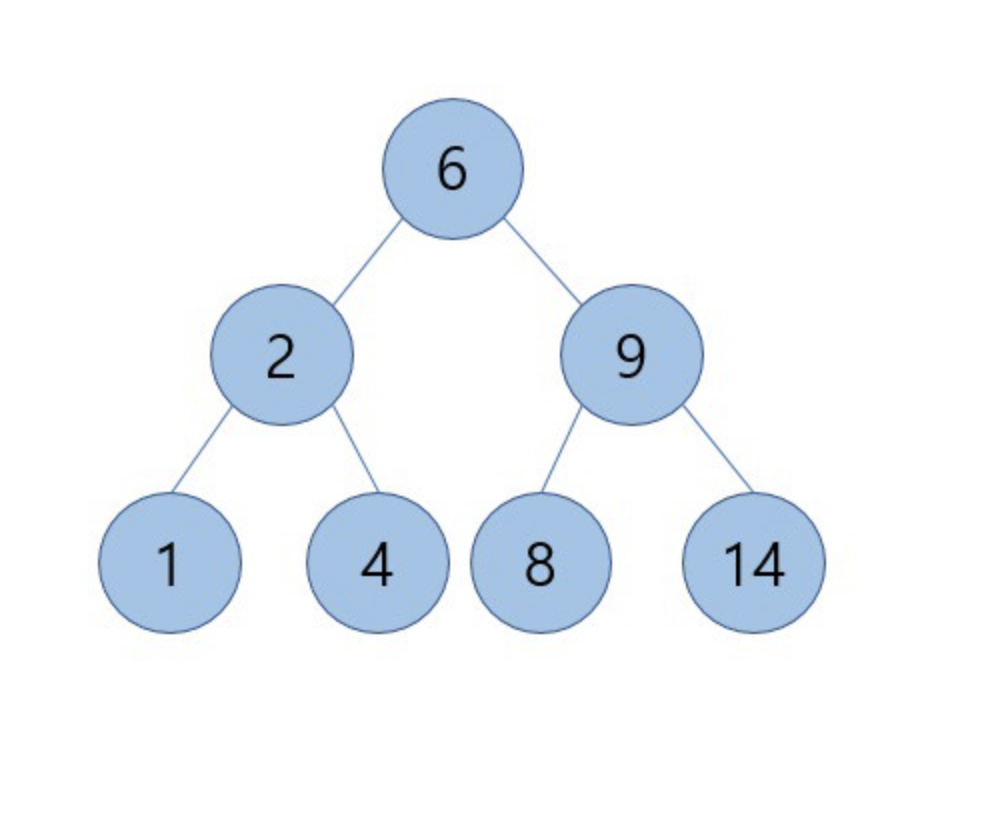
아래 이진탐색트리에서 11을 삭제하려고 할 때, 11은 자식노드가 1개만 있는 경우이므로 11을 삭제하고 9와 14를 연결시켜줍니다.

14를 루트로 하는 서브트리의 모든 키값은 9보다 크기 때문에 그냥 연결해도 이진탐색트리의 조건에 위배 되지 않습니다.

3) 삭제하려는 노드의 자식 노드가 2개인 경우

해당 노드를 삭제하고 해당 노드의 predecessor(왼쪽 서브트리의 최대값) 또는 successor(오른쪽 서브트리의 최소값)으로 대체 합니다. predecessor와 successor는 자식노드가 존재하지 않거나 자식노드가 하나만 존재 합니다.

아래 이진탐색트리에서 9를 삭제 해보겠습니다.

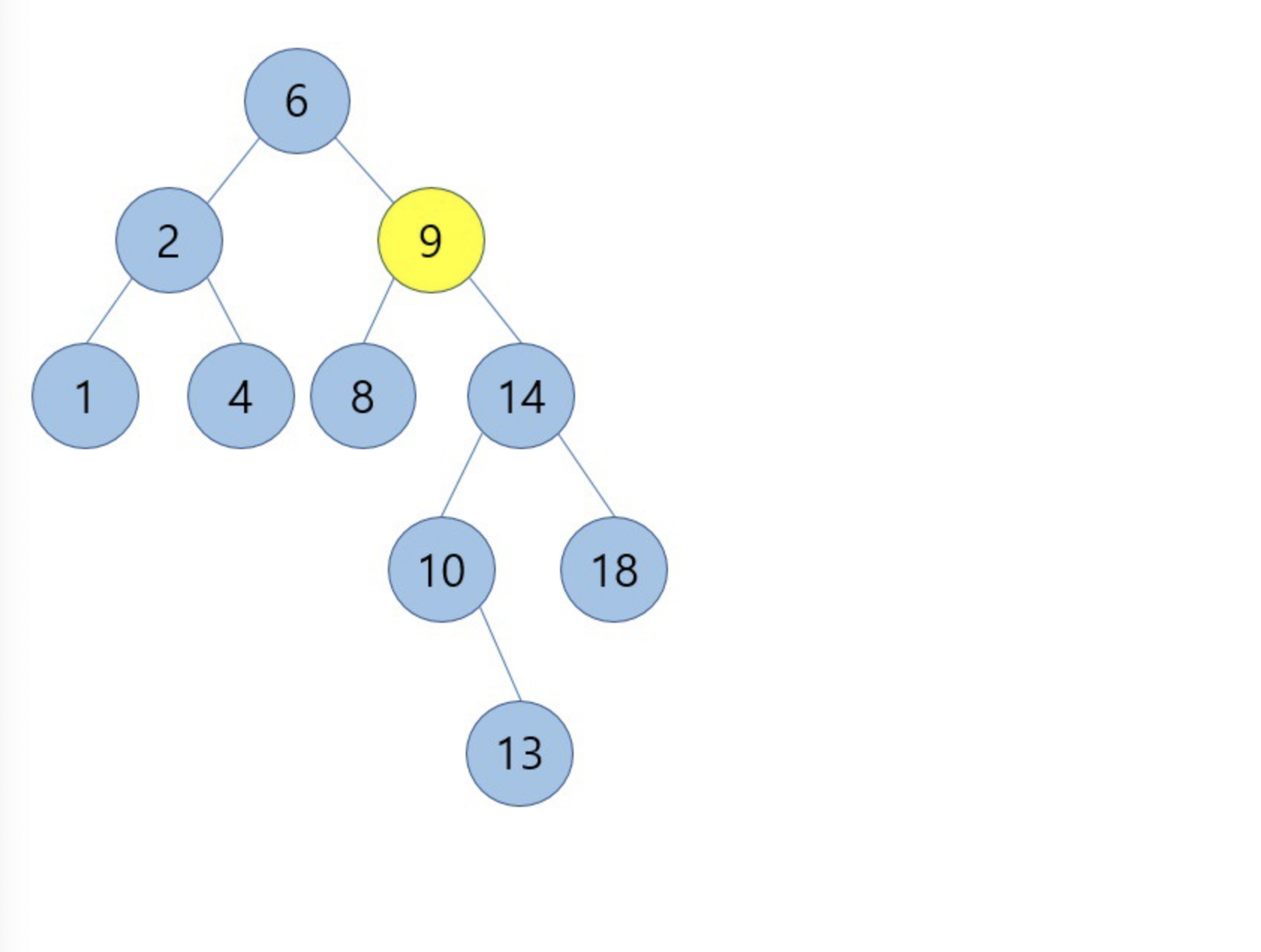
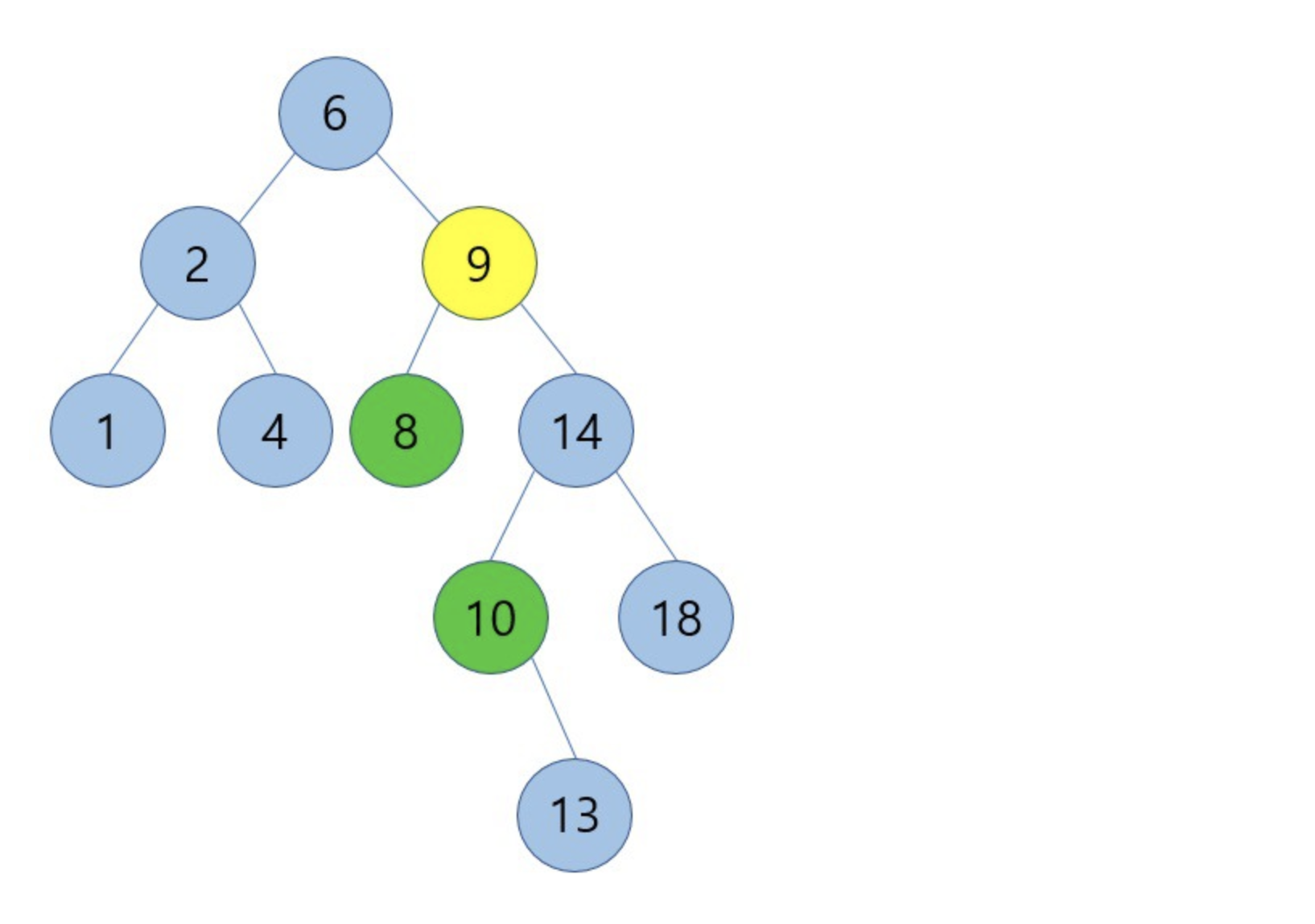
여기서 삭제될 9의 위치에 올 수 있는 노드는 predecessor인 8과 successor인 10이 됩니다.

8은 9의 왼쪽 서브트리에서 최대값이며 10은 9의 오른쪽 서브트리에서 최소값이기 때문입니다.

9를 삭제하고 predecessor인 8을 9의 자리로 옮겼을 때 결과는 아래와 같습니다.

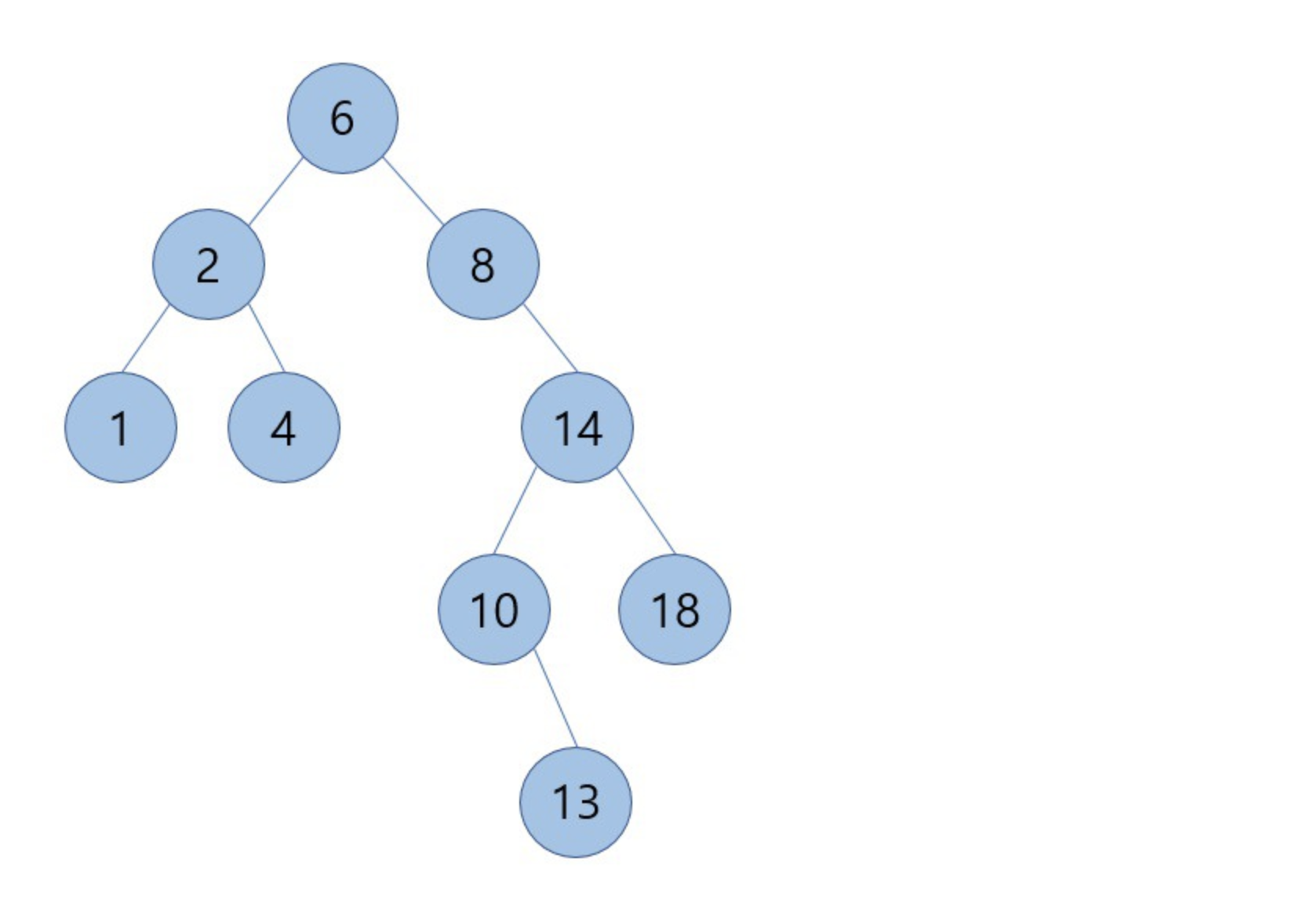
predecessor인 8은 자식노드가 존재하지 않았기 때문에 9의 위치에 8을 놓고 기존 8의 위치에 있는 노드는 삭제합니다.

9를 삭제하고 successor인 10을 옮기는 경우를 해보면

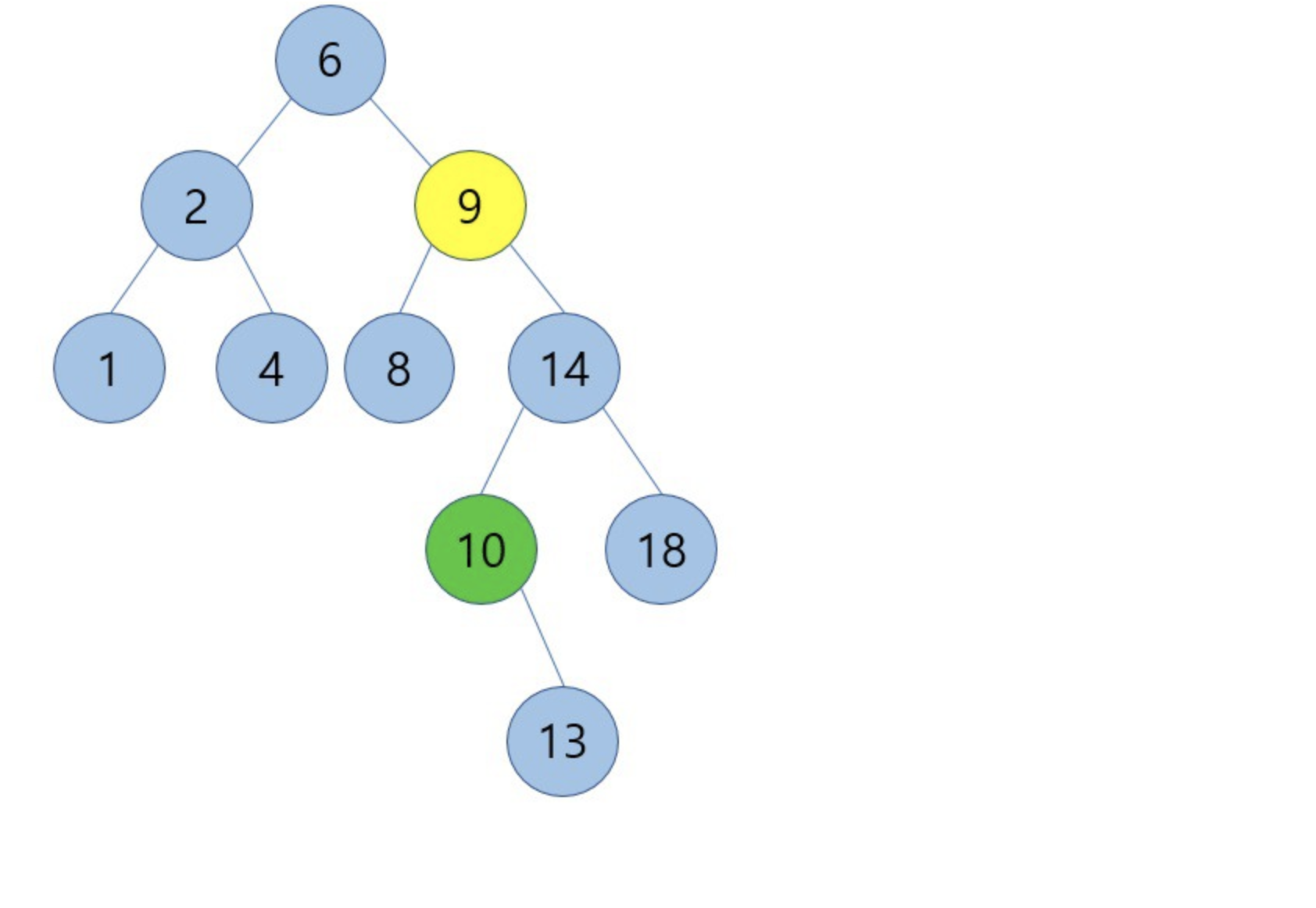
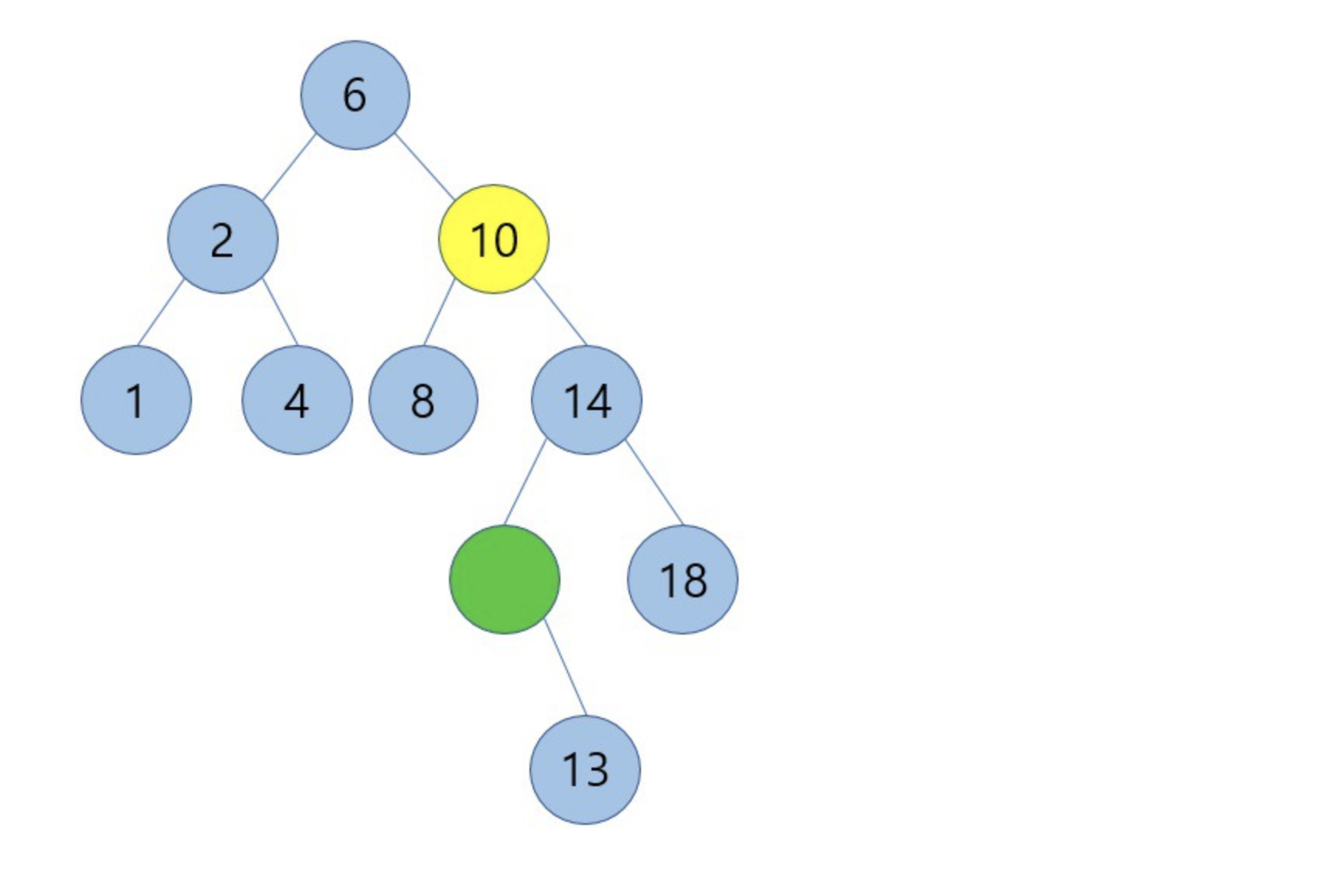
위의 그림과 같은 결과를 가지게 됩니다.

여기서 눈여겨 볼 점은 처음에 삭제할 노드 9를 기준으로 successor였던 10은 자식노드를 1개 가지고 있다는 점입니다.

이는 자식노드가 1개만 존재하는 삭제 연산 두번째 케이스에 해당됩니다. 따라서 기존 successor 10의 자식노드인 13과 successor 10의 부모노드인 14를 연결시킨 것이고 이진탐색트리의 조건에 위배되지 않습니다.

자식노드가 1개인 predecessor를 옮기는 경우도 마찬가지입니다.

이진 검색트리의 문제점

이진 검색트리를 만족하지만 문제가 되는 경우가 있습니다.

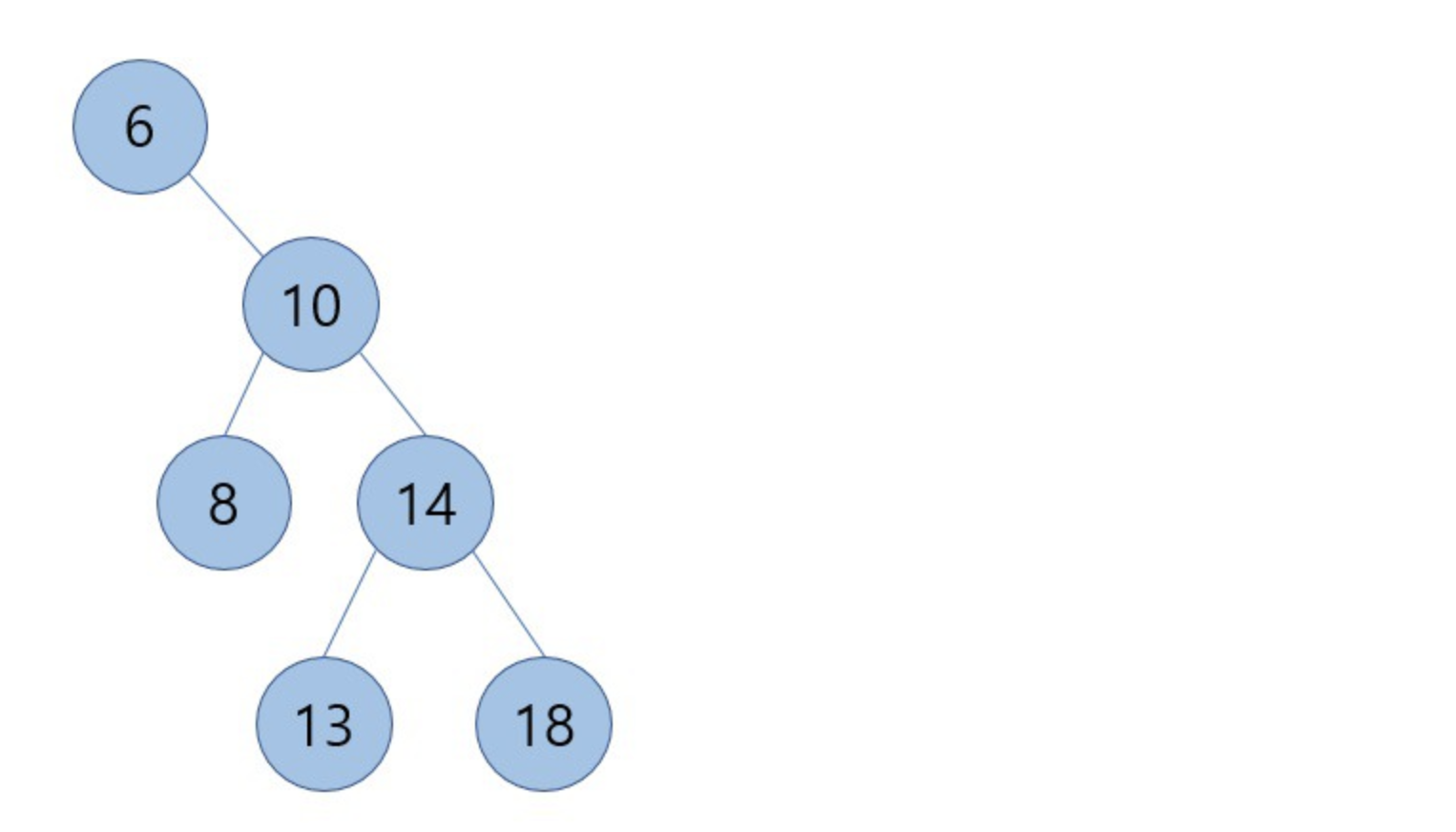
이 이진검색트리는 노드가 6개지만 높이는 3이 됩니다.

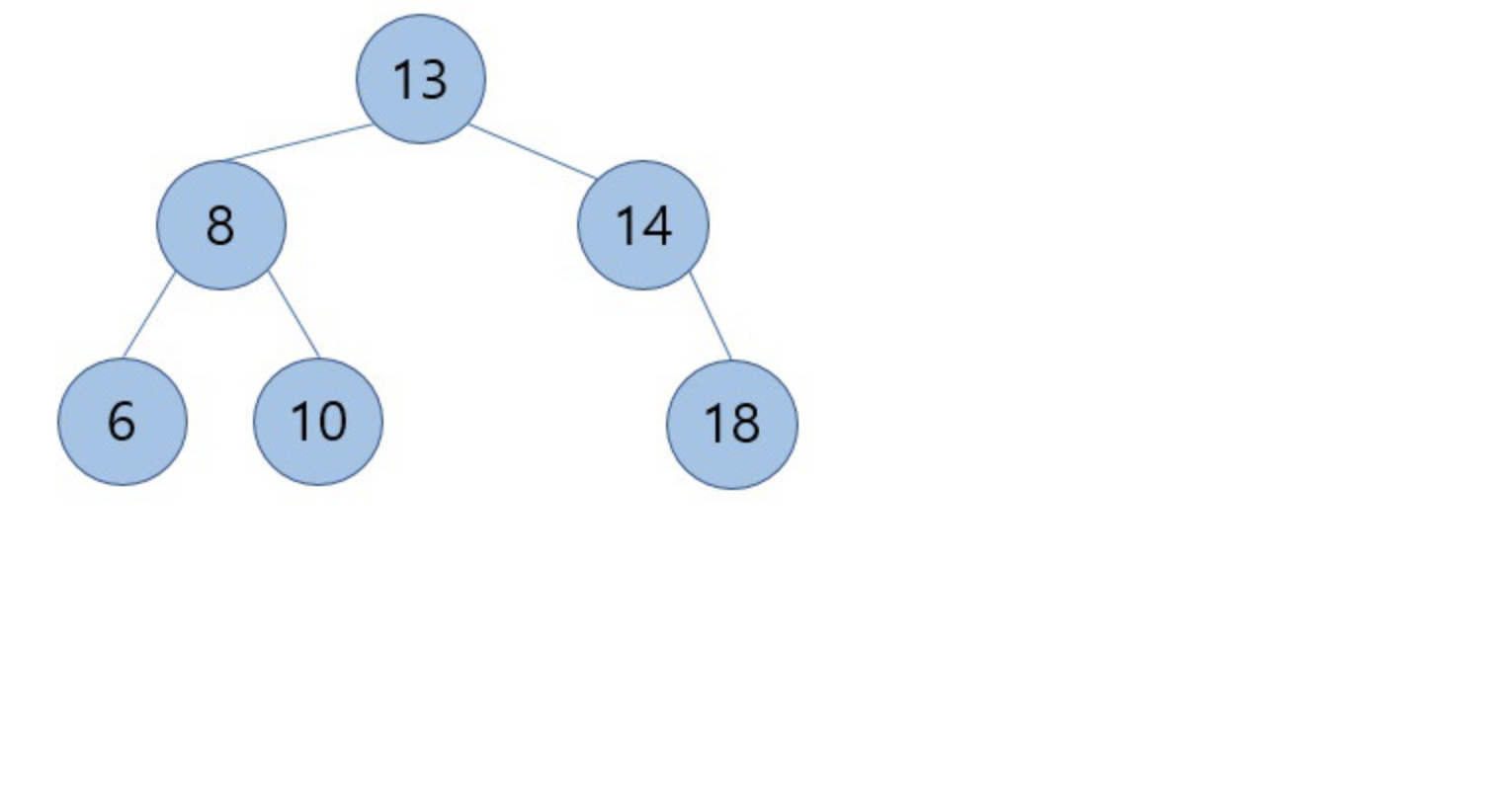
위의 이진 검색트리는 위의 트리와 같은 노드의 수, 같은 키값을 가집니다.
하지만 이 이진 검색트리는 높이가 2 입니다. 전자보다 높이가 낮고 균형이 잘 잡혀 있습니다.

만약 이진 검색트리가 극단적인 구조를 가지게 될 경우 한 쪽으로만 계속 늘어지는 구조를 가지게 될 것이다. 이런 경우 시간 복잡도가 O(n)이 됩니다.

이러한 문제를 해결한 것이 AVL트리입니다.

AVL 트리는 이진 탐색의 장점을 살리면서 균형이 깨지는 단점을 해결 하였습니다.