1. 트리
What is tree?
트리는 비선형 구조의 데이터 구조입니다. 스택, 큐, 연결리스트의 자료구조들은 선형구조로 이루어져있었지만 트리는 한 노드에 두개 이상의 자식 노드를 가짐으로서 비선형 구조를 가지게 됩니다.

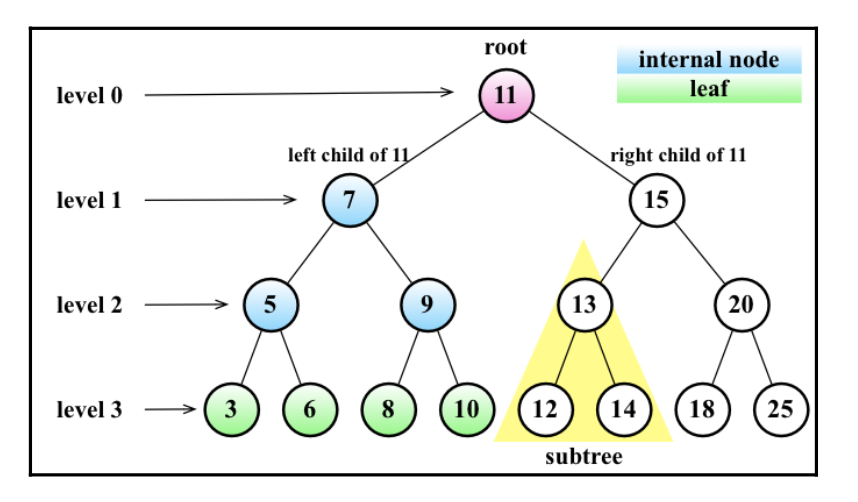
위의 그림을 보면 가장 위에 있는 노드를 root라고 표기 한 것을 볼 수 있습니다. 가장 위에 있는 노드는 당연하게도 부모 노드를 가질 수 없습니다. 노드는 최소 한개 이상의 노드를 가집니다. 만약 노드들이 자식을 가지지 않는다면 이때 leaf라고 불립니다.
트리의 높이는 어느 노드의 최대 깊이로 구성이 됩니다. root 가장 위에 있는 노드는 level 0 그 자식은 level1 ... 계속 해서 자식의 노드로 내려 갈 수록 레벨은 하나씩 높아집니다.
위의 그림을 보면 root부터 leaf까지의 level이 3으로 구성 되어 있고 이 트리의 최종 레벨은 3이 됩니다.
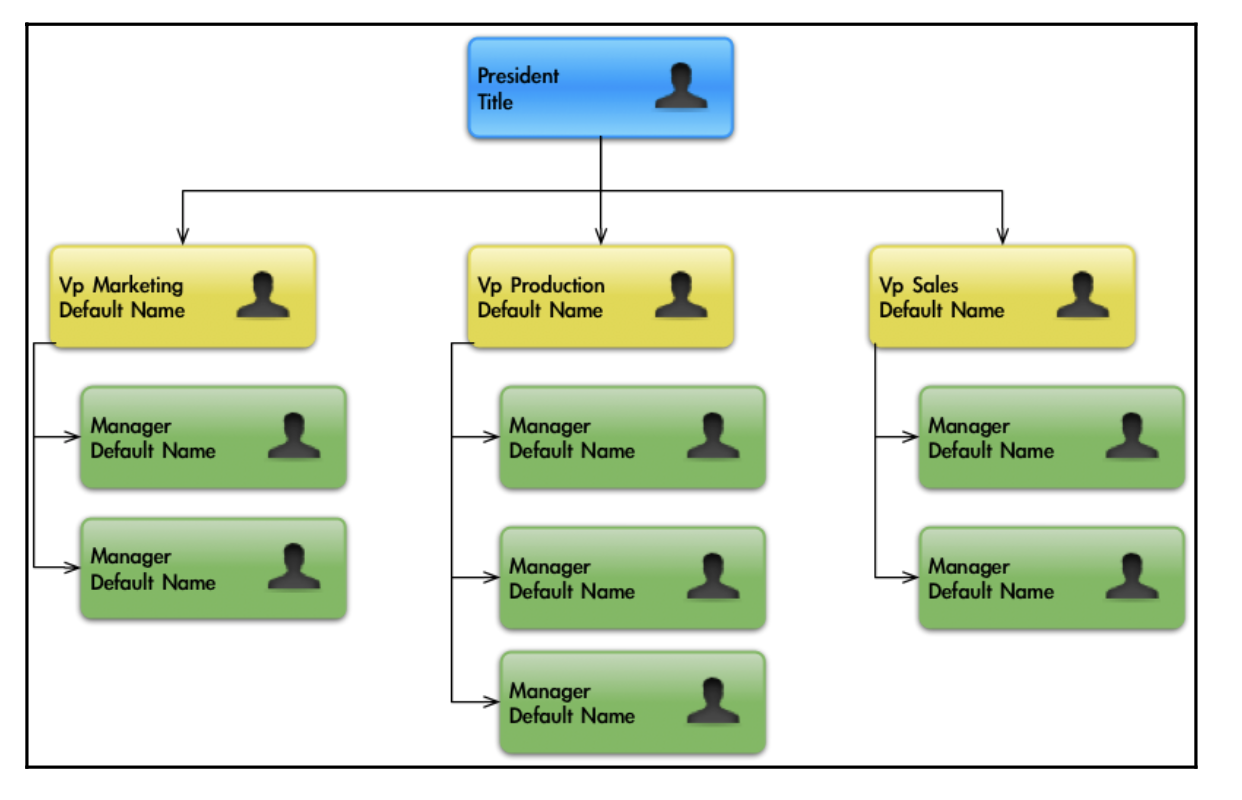
위의 그림은 실생활에서의 트리 구조입니다. 위의 그림으로 보아 트리는 계층으로 구성이 되어 있다는 것을 알 수 있습니다.
트리의 종류
트리에 종류 중 이진트리와, 이진탐색트리에 대해 알아 보겠습니다. 이진 트리의는 자식 노드를 두개 까지 가집니다. 이러한 트리 구조는 검색, 삽입, 삭제를 더욱 용이하게 해줍니다.
이진트리에서 새로운 특징이 있는 것이 이진 검색 트리입니다.
이진 검색트리는 부모의 좌측 자식 노드의 값이 더 작은 수 우측 자식 노드의 값이 더 큰 수로 구성이 됩니다.
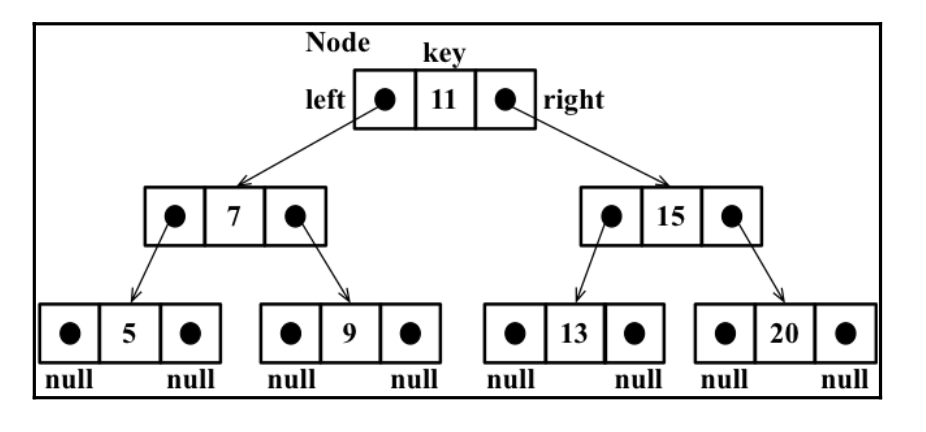
위의 그림은 이진 검색트리의 구성 그림입니다. 위의 그림을 보면 각각의 노드들은 하나의 키와 양 옆에 다음 자식 노드를 값이 구성 되어 있는 것을 볼 수 있습니다.
이를 토대로 이진 검색트리의 구성을 작성 해보면 아래 코드와 같이 노드를 구성 하게 됩니다.
이진 트리의 노드
function BinarySearchTree() {
var Node = function(value){
this.value = value;
this.left = null;
this.right = null;
};
}트리의 순회
트리의 순회는 트리의 모든 노드들을 방문하는 과정입니다. 모든 노드들을 방문하는데에 있어서 여러 가지 방법이 있을것 같습니다. 여기서 생각을 해보면 반드시 위에서 아래로 즉 부모노드에서 자식노드로만 순회를 해야 할까요?? 의문점이 생길거 같습니다. 왼쪽에서 오른쪽으로 방문하는 방법이 있지도 않을까요? 여기에서 3가지 노드들을 방문 순회하는 접근법이 나옵니다. 트리를 방문 순회하는 방법에는 전위순회(pre-Order), 중위순회(in-Order), 후위순회(post-Order)가 있습니다.
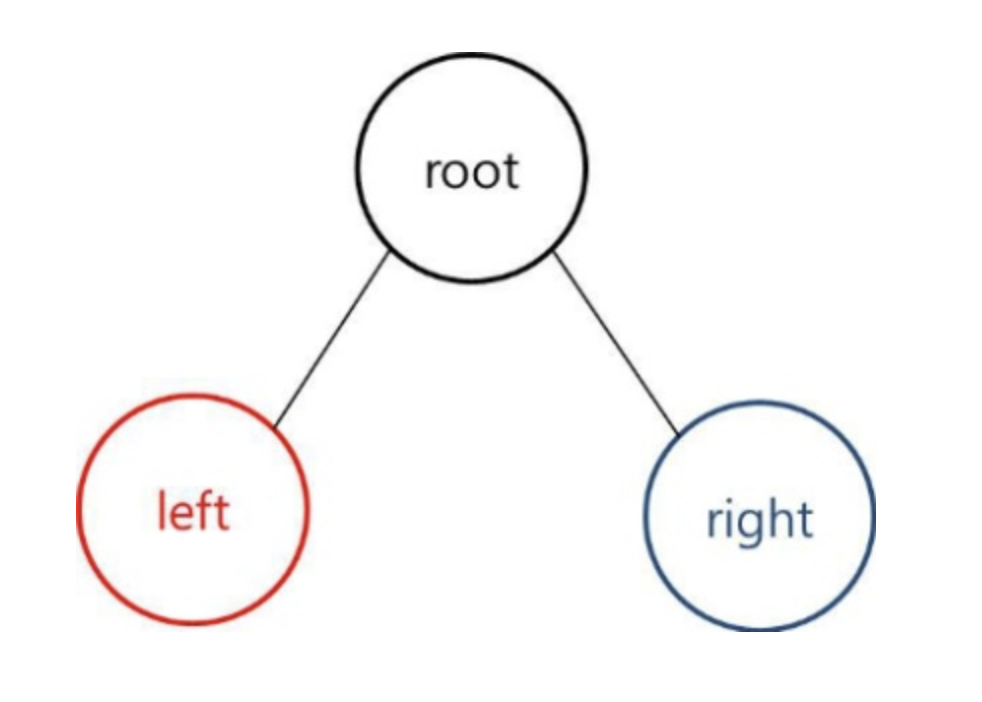
rootNode를 D, leftNode를 L rightNode를 R이라고 해봅시다.
전위 순회 (pre-order Traversal)
전위 순회 방법은 트리를 D-L-R순으로 순회하는 방법입니다.
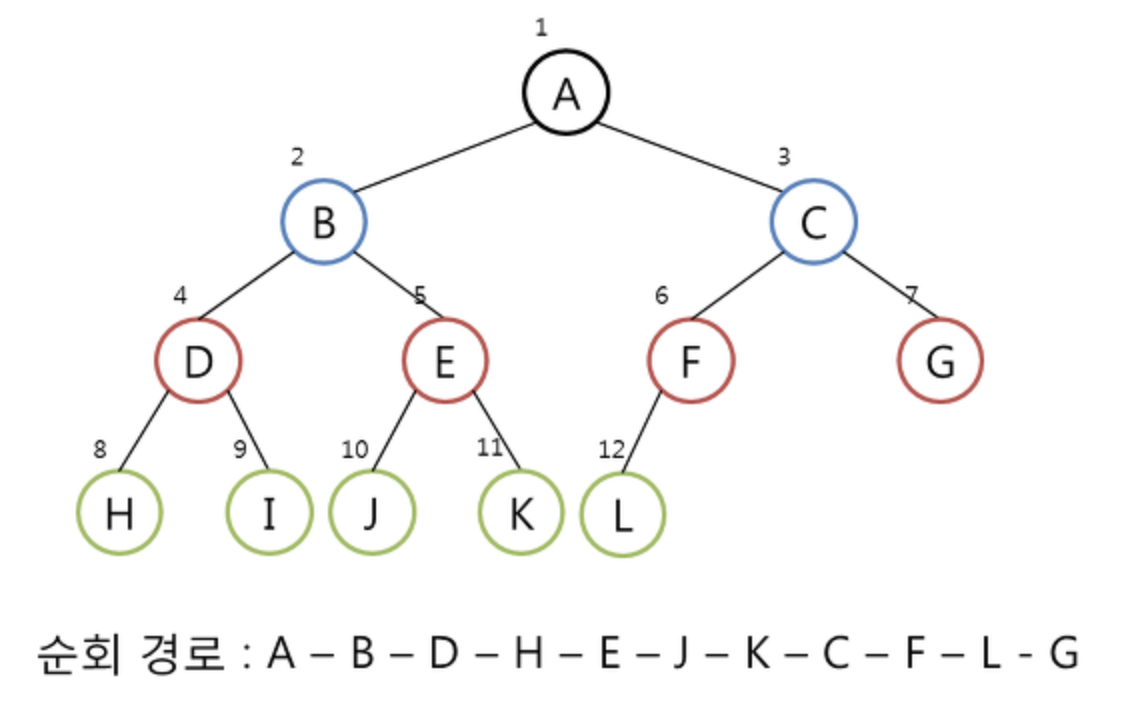
전위 순회로 트리를 순회 했을때 나오는 경로입니다.
중위 순회 (In-order Traversal)
중위 순회 방법은 트리를 L-D-R의 순서로 순회하는 방법입니다.
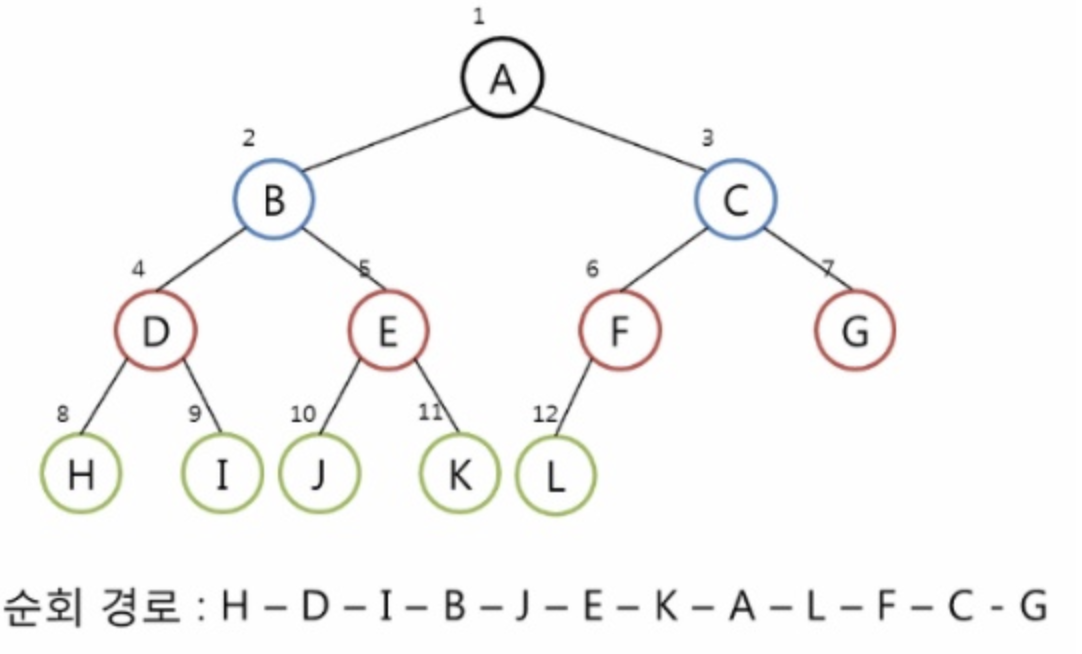
중위 순회로 트리를 순회 했을때 나오는 경로입니다.
후위 순회 (In-order Traversal)
후위 순회 방법은 트리를 L-R-D의 순서로 순회하는 방법입니다.
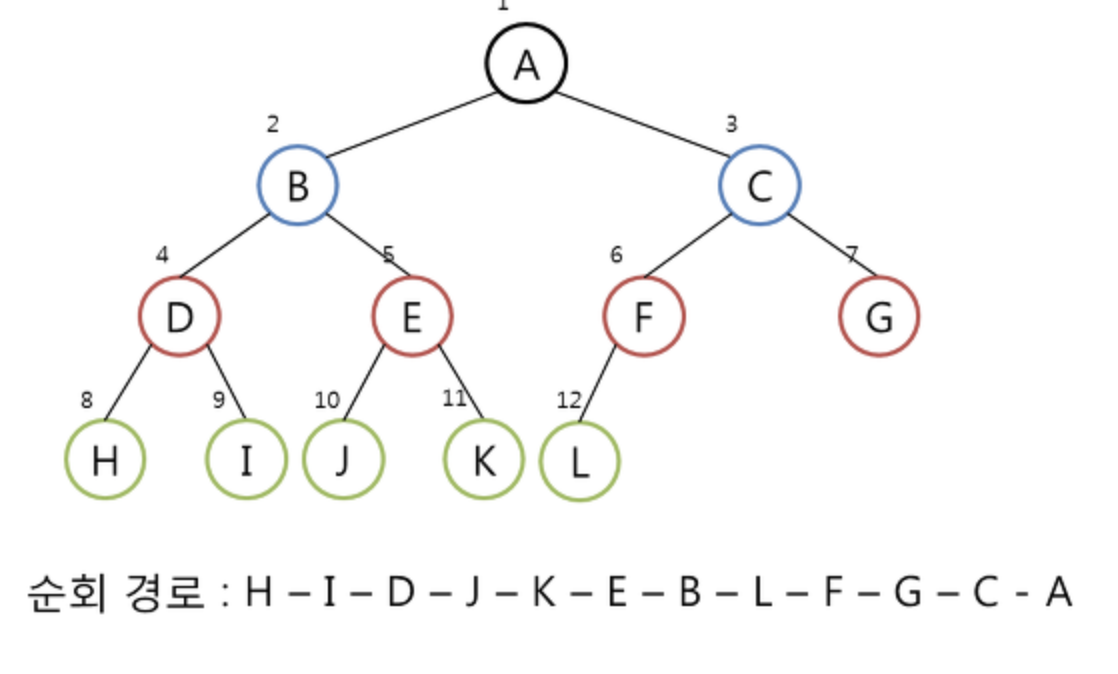
후위 순회로 트리를 순회 했을때 나오는 경로입니다.
이진 검색트리의 property
* node : 트리의 노드
* value : 노드의 값
* left : 왼쪽 자식
* right : 우측 자식 이진 검색트리의 Method
* insert : 삽입
* search : 검색
* remove : 삭제
* min : 최솟값
* max : 최댓값
* inOrder : 중위 순회
* preOrder : 전위 순회
* postOrder : 후위 순회 2. 그래프
what is graph?
그래프는 다음 그림과 같이 정점(vertex)와 간선(edge)로 이루어진 구조를 말합니다. 그래프는 방향성을 가질 수 있는데 방향성이 없으면 undirected graph, directed graph로 나뉩니다.
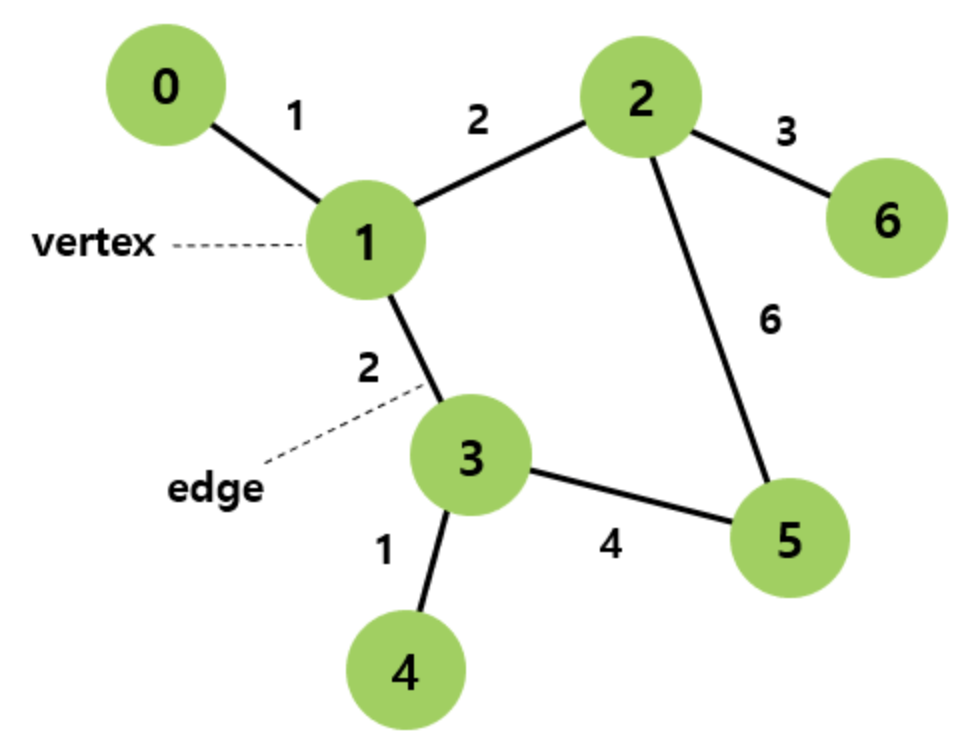
아래는 방향성이 있는 그래프입니다. 방향성을 가진 그래프는 화살표로 나타 낼 수 있고 사로 다른 정점이 서로를 향해 방향을 가르킬수 있습니다.
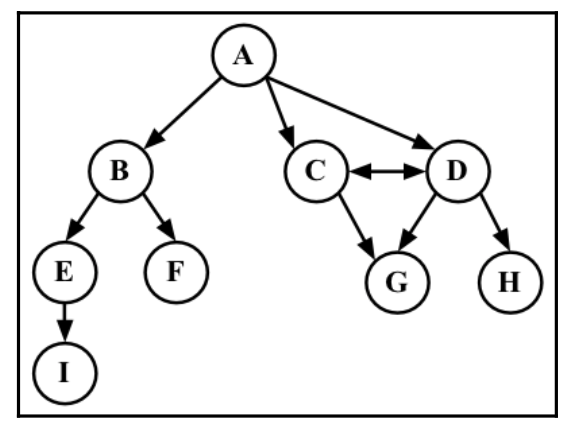
아래의 그림을 보면 숫자가 쓰여 있는데 방향성을 가지는 정점은 가중치(weight)를 가지게 됩니다.

Degree
방향이 없는 그래프 (undirected Graph)에서 각 정점(vertex)에 연결된 Edge의 개수를 Degree라 합니다. 방향이 있는 그래프(Directed Graph) 에서는 간선에 방향성이 존재하기 때문에 Degree가 두개로 나뉘게 됩니다. 각 정점으로 부터 나가는 간선의 개수를 outdegree라 하고, 들어오는 간선의 개수를 indegree라고 합니다.
가중치 그래프(weight Graph)와 부분 그래프 (sub Graph)
가중치 그래프란 간선에 가중치 정보를 두어서 구성한 그래프를 말합니다. 반대의 개념인 비가중치 그래프 즉 모든 간선의 가중치가 동일한 그래프도 존재합니다.
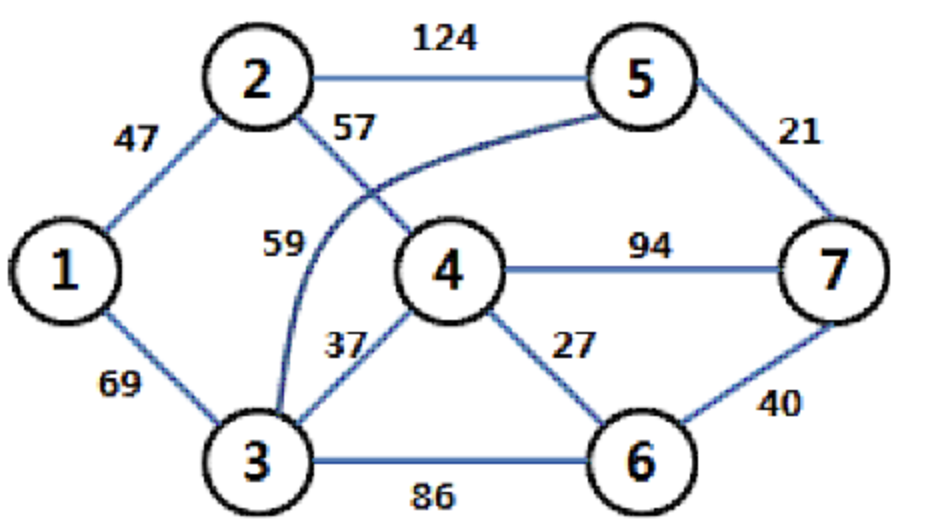
그래프의 proprety
* V(vertices) : 정점(노드)
* E(edge) : 간선 그래프 Method
* addNode : 노드(정점) 추가
* contains : target노드 확인
* removeNode : 해당 노드(정점) 삭제
* hasEdge : target 간선 확인
* addEdge : 간선 추가
* removeEdge : 간선 제거
* forEachNode : 정점 순회