[Linear Algebra] Geometric Understanding of Linear Dependence

Geometric Understanding of Linear Dependence

e.g.

Given two vectors $\textbf{v}_1$ and $\textbf{v}_2$, suppose $\textrm{Span}\begin{Bmatrix} \textbf{v}_1, \textbf{v}_2 \end{Bmatrix}$ is the plane below

if the third vector $\textbf{x} \in \textrm{Span}\begin{Bmatrix} \textbf{v}_1, \textbf{v}_2 \end{Bmatrix}$, then the vector $\textbf{x}$ is linearly dependent of $\textbf{v}_1$ and $\textbf{v}_2$

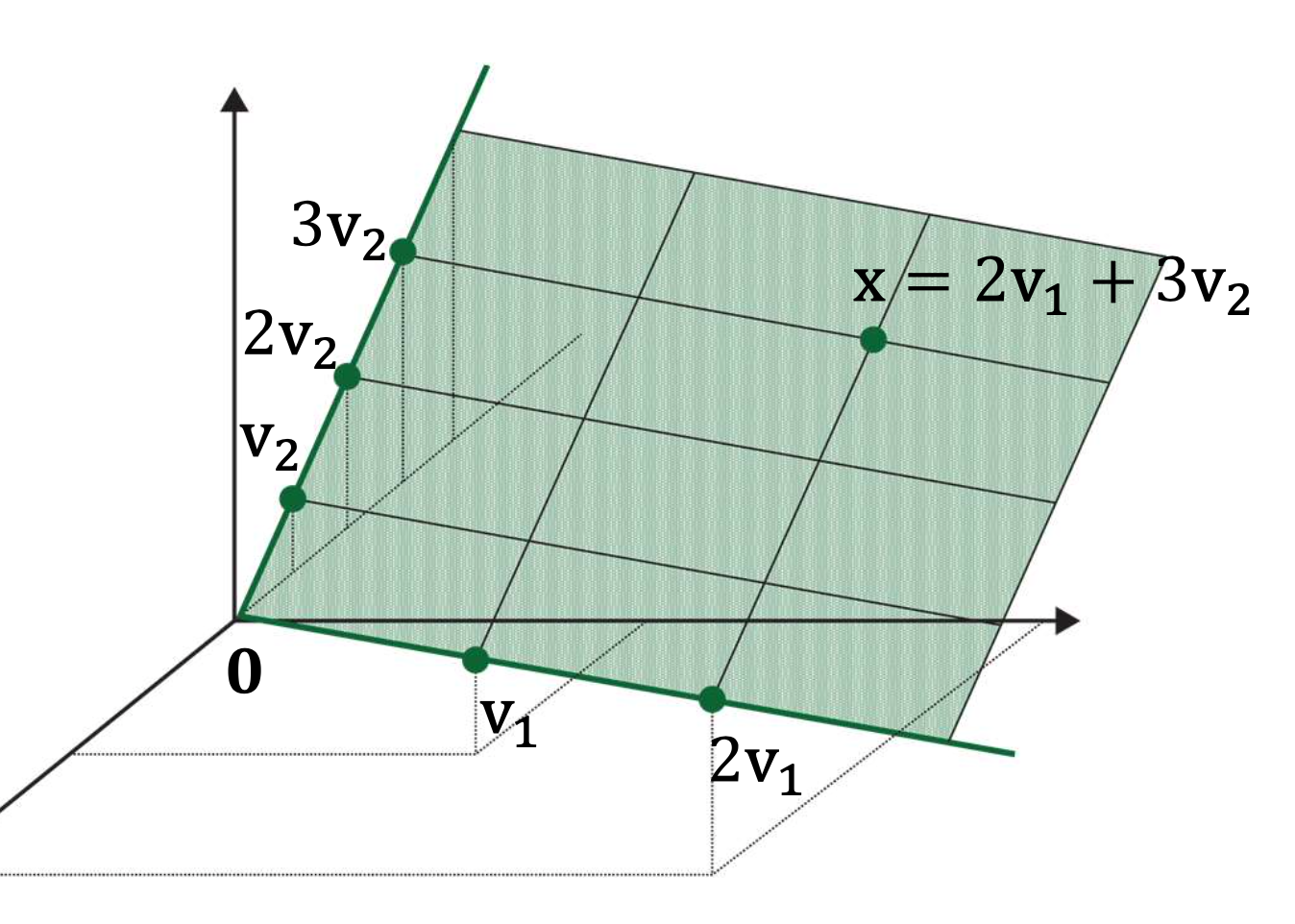
Linear Dependence

A linear dependent vector does not increase $\textrm{Span}$

If $\textbf{v}_3 \in \textrm{Span}\begin{Bmatrix} \textbf{v}_1, \textbf{v}_2 \end{Bmatrix}$, then $\textrm{Span}\begin{Bmatrix} \textbf{v}_1, \textbf{v}_2 \end{Bmatrix} = \textrm{Span}\begin{Bmatrix} \textbf{v}_1, \textbf{v}_2 , \textbf{v}_3 \end{Bmatrix}$

Linear Dependence and Linear System Solution

A linearly dependent set produces multiple possible linear combinations of a given vector