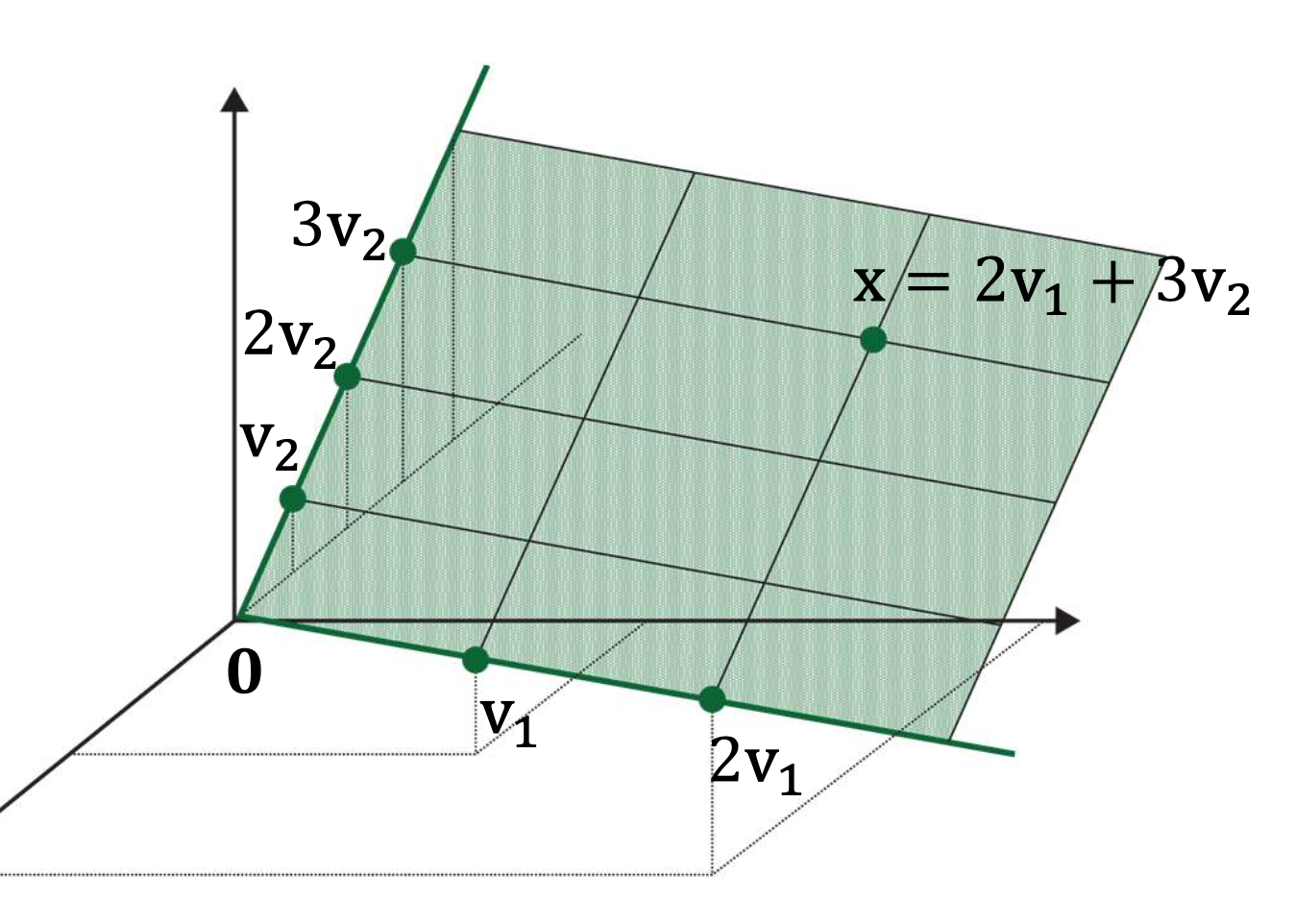
Span and Subspace
- Definition : A subspace is defined as a subset of closed under linear combination
For any two vectors and any two scalars ,
- is always a subspace
- Subspace is always represented as
Basis of a Subspace
- Definition : a basis of a subspace is a set of vectors that satisfies both the following
- Fully spans the given subspace
- Linearly independent (i.e. no redundancy)
Non-Uniqueness of Basis
- Consider a subspace , green plane
- Basis of a subspace is not unique