[Linear Algebra] Onto One-to-one

ONTO and ONE-TO-ONE

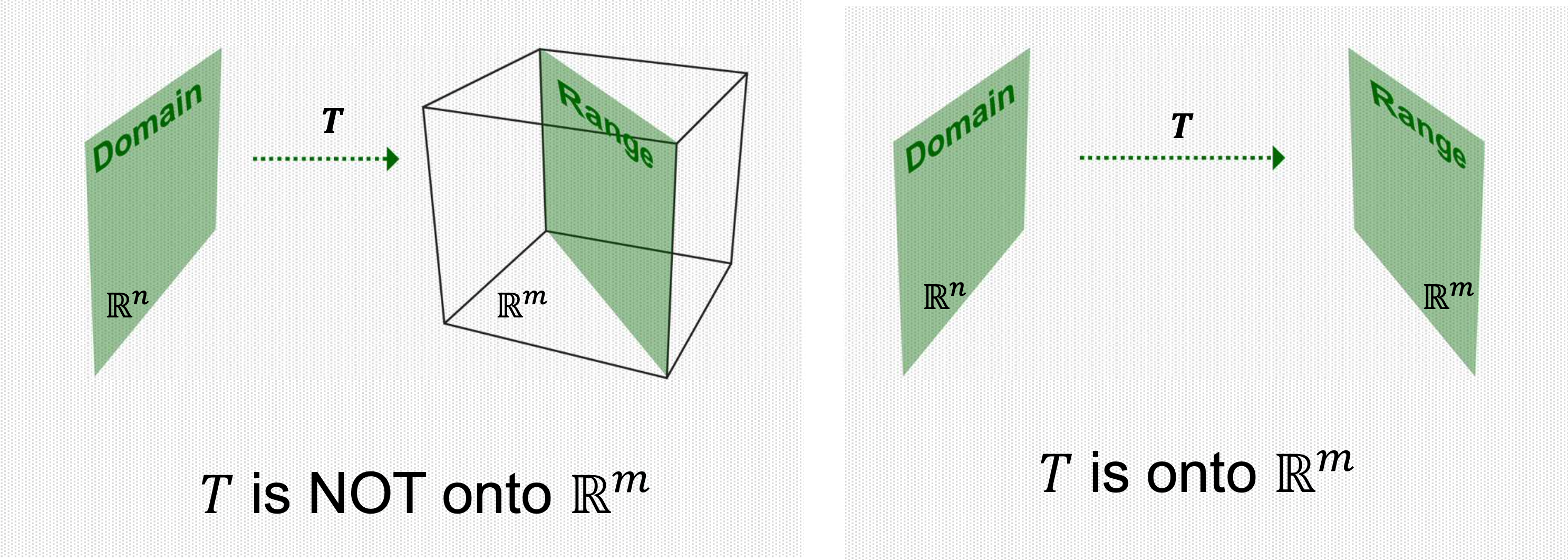
• Defintion of ONTO
  • A mapping $T : \mathbb{R}^n \mapsto \mathbb{R}^m$ is said to be onto $\mathbb{R}^m$ if each $\textbf{b} \in \mathbb{R}^m$ is the image of at least one $\textbf{x} \in \mathbb{R}^n$
  • That is, the range is equal to the co-domain

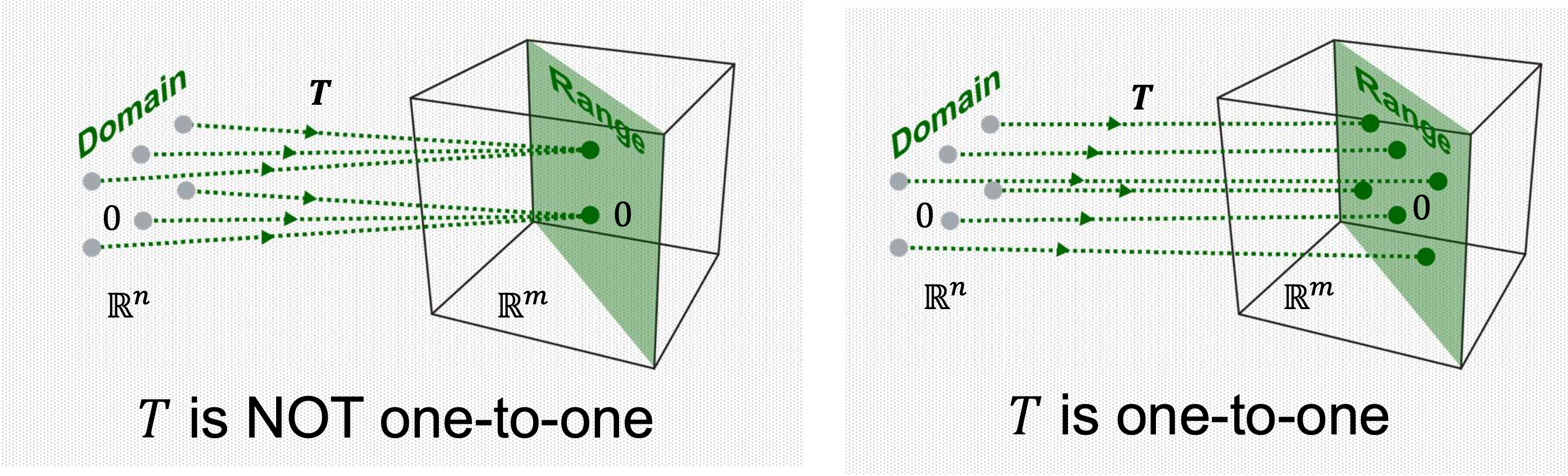
• Definition of ONE-TO-ONE
  • A mapping $T : \mathbb{R}^n \mapsto \mathbb{R}^m$ is said to be one-to-one if each $\textbf{b} \in \mathbb{R}^m$ is the image of at most one $\textbf{x} \in \mathbb{R}^n$
  • That is, each output vector in the range is mapped by only one input vector

• Domain : set of all the possible values of x
• Co-domain : set of all the possible values of y
• Image : a mapped output y, given x
• Range : set of all the output values mapped by each x in the domain

Let $T : \mathbb{R}^n \mapsto \mathbb{R}^m$ be a linear transformation

• $T(\textbf{x}) = A\textbf{x}$ for all $\mathbf{x} \in \mathbb{R}^n$
  • $T$ is one-to-one if and only if the columns of $A$ are linearly independent
  • $T$ maps $\mathbb{R}^n$ onto $\mathbb{R}^m$ if and only if the columns of $A$ span $\mathbb{R}^m$