오늘은 데이터셋을 이용하여 모형을 출력하는 법과 레버리지와 이상치에 대해 배워보려고합니다.
레버리지(leverage)
레버리지란 실제 종속변수값(y)가 예측치(predicted target)에 미치는 영향을 나타낸 값입니다.
이상치(outlier)
이상치란 관측된 데이터 범위에서 매우 크거나 작은 값으로 데이터의 범위를 많이 벗어난 값들을 말합니다.
가상데이터셋 설정
input
from sklearn.datasets import make_regression
#랜덤 데이터셋
X0, y, coef=make_regression(n_samples=100, n_features=1, noise=20, coef=True, random_state=1)make_regression 함수를 이용하여 가상데이터 셋을 만들어줍니다.
이상치 추가
input
import numpy as np
import statsmodels.api as sm
#이상치 추가
data_100=(4,300)
data_101=(3,150)
X0=np.vstack([X0, np.array([data_100[:1],data_101[:1]])])
X=sm.add_constant(X0) #상수항 1 추가
y=np.hstack([y,[data_100[1],data_101[1]]])이상치를 넣었을 때 값 변동을 알아보기 위해 이상치를 추가해 줍니다.
데이터 시각화
input
import matplotlib.pyplot as plt
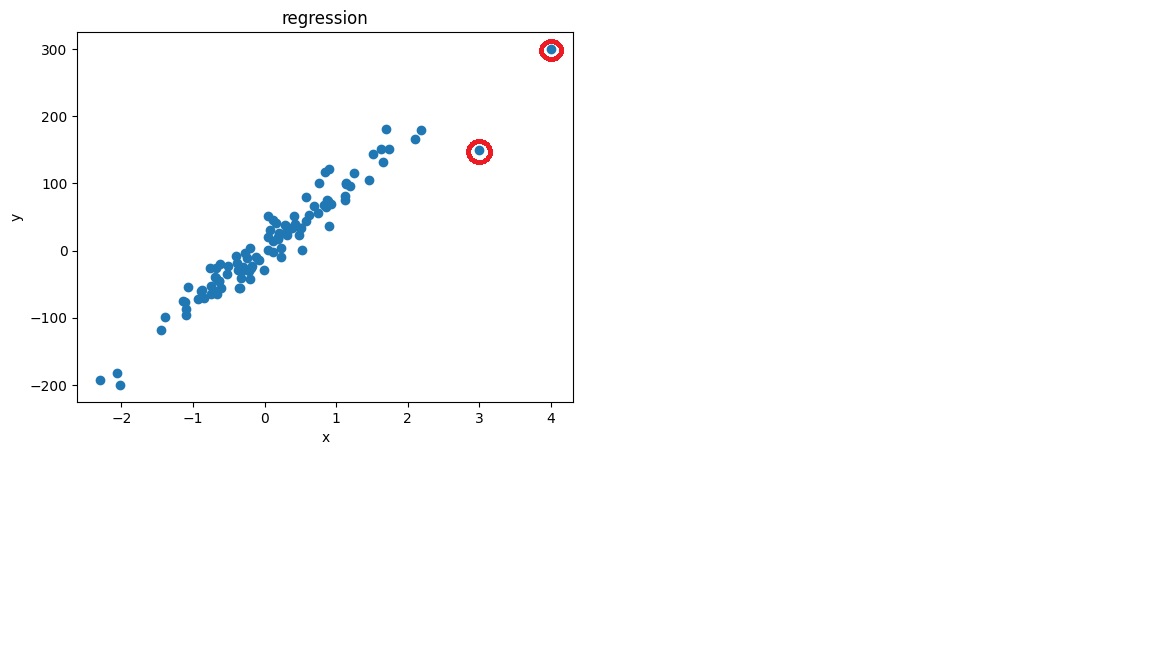
plt.scatter(X0,y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('regression')output
(4,300)과 (3,150) 이라는 이상치를 넣었기 때문에 시각화한 자료에도 적용된 것을 확인 할 수 있습니다.
데이터 요약본 출력
input
import pandas as pd
model=sm.OLS(pd.DataFrame(y),pd.DataFrame(X))
result=model.fit()
result.summary()output
모델을 OLS로 생성 및 학습시켜 줍니다,
레버리지(leverage) 출력
input
#레버리지(leverage) : 실제값이 예측값에 미치는 영향을 나타낸 값
# 0~1 사이의 값
influence=result.get_influence() # 영향도 값
hat=influence.hat_matrix_diag # 레버리지 벡터의 값
plt.figure(figsize=(10,2))
plt.stem(hat) # 가로폭이 없는 그래프
plt.axhline(0.02, c='g', ls='--')
plt.title('leverage')
# 이상치의 leverage가 크게 표현됨output
그래프에서 0.02라는 선을 임의로 설정했습니다. 그 이상 초과하는 값들을 영향이 많다고 판단 하기 편하기 위함입니다.
레버리지 값 강조
input
ax=plt.subplot()
plt.scatter(X0,y)
sm.graphics.abline_plot(model_results=result, ax=ax)
idx=hat>0.05
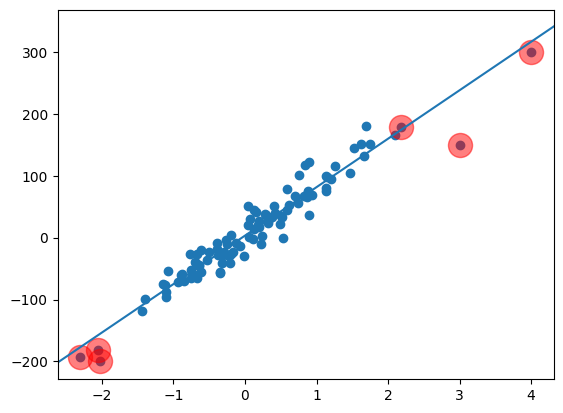
plt.scatter(X0[idx],y[idx],s=300,c='r',alpha=0.5)
plt.show()
#레버리지가 0.05보다 큰 샘플 강조output
그 중에서도 레버리지가 높은 데이터가 존재합니다
데이터 삭제
input
model2=sm.OLS(y[:-1],X[:-1]) #마지막 샘플을 제외한 모형
result2=model2.fit()
ax=plt.subplot()
plt.scatter(X0,y)
sm.graphics.abline_plot(model_results=result, c='r',linestyle='--',ax=ax,label='A')
sm.graphics.abline_plot(model_results=result2, c='g',alpha=0.7,ax=ax,label='B')
plt.plot(X0[-1],y[-1],marker='x',c='m',ms=20,mew=5) #마지막 샘플의 좌표
plt.legend()
plt.show()output
기울기에서 가장 많이 벗어난 데이터 하나를 삭제해 해 줍니다.
데이터 잔차 확인
input
plt.figure(figsize=(10,2))
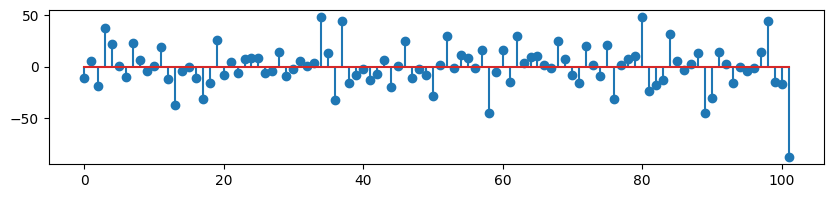
plt.stem(result.resid) #샘플의 잔차 그래프
plt.show()output
데이터의 잔차를 확인하기 위해 stem과 resid 함수를 이용하여 출력합니다.
데이터 표준화
input
plt.figure(figsize=(10,2))
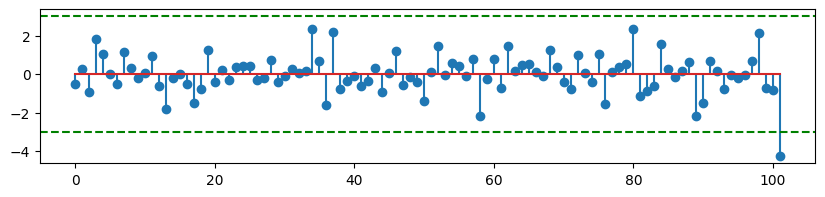
plt.stem(result.resid_pearson) #표준화 잔차
plt.axhline(3,c='g',ls='--')
plt.axhline(-3,c='g',ls='--')
plt.show()output
데이터 잔차 값이 -50~50이란 값이 크기 때문에 표준화 후 잔차를 출력해 줍니다.
레버리지 시각화
input
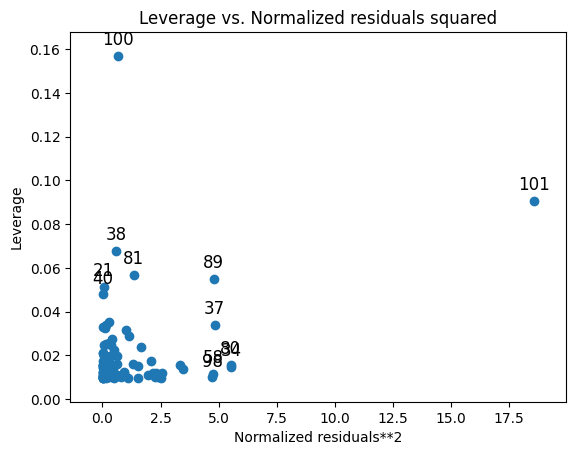
sm.graphics.plot_leverage_resid2(result)
plt.show()
# 100번 샘플 - 레버리지가 크게 나타남
# 101번 샘플 - 레버리지와 잔차가 크게 나타남output
이상치 시각화
input
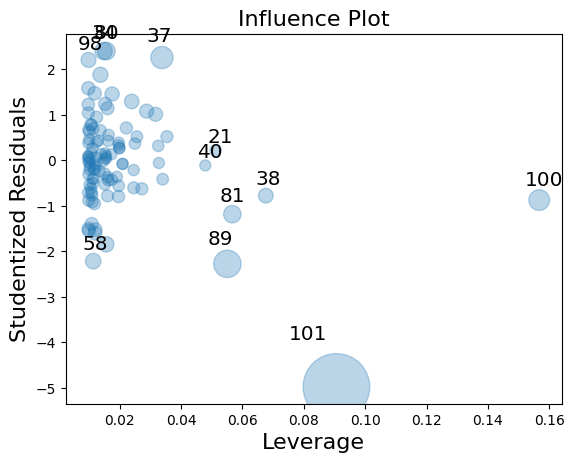
sm.graphics.influence_plot(result, plot_alpha=0.3)
plt.show()
# 100,101번 이상치output
이상으로 오늘은 레버리지와 이상치에 대해 배워보았습니다. 데이터의 이상치가 있을 때와 레버리지값이 이상할 때는 어떤 데이터인지 어떤식으로 처리해야 좋을지 생각해 보는 것이 중요하다고 생각합니다. 해당 데이터 값으로 인해서 정확도가 떨어지는 경우도 많다고 생각합니다.