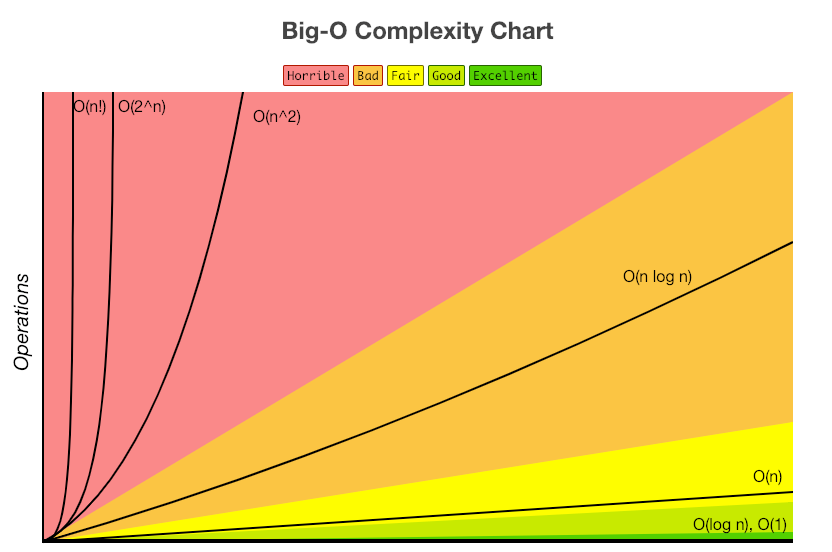
Time Complexity

입력된 N의 크기에 따라 실행되는 조작의 수
근데 왜 'time' complexity라고 해놓고, 정작 복잡도 계산은 '연산 횟수'로 판별하는지?
https://blog.chulgil.me/algorithm/ => 해당 출처에 따르면 실행 시간 자체는 hw, language 등에 따라 편차가 커서 그렇단다.
time complexity를 뜻하는 big-O notation의 단계를 나열해보면,

O(1) : 입력값 크기에 관계없이 문제가 해결됨
O(log n) : 문제 해결에 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬
O(n) : 문제 해결에 필요한 단계의 수와, 입력 값 n이 1:1
O(nlogn) : 문제 해결에 필요한 단계의 수가 Nlog2N번만큼 수행시간을 가짐
O(${n^2}$) : for 문이 두번 중첩된 케이스
O(${C^n}$)
O(N!)

Big-O notation(can estimate time & space complexity)

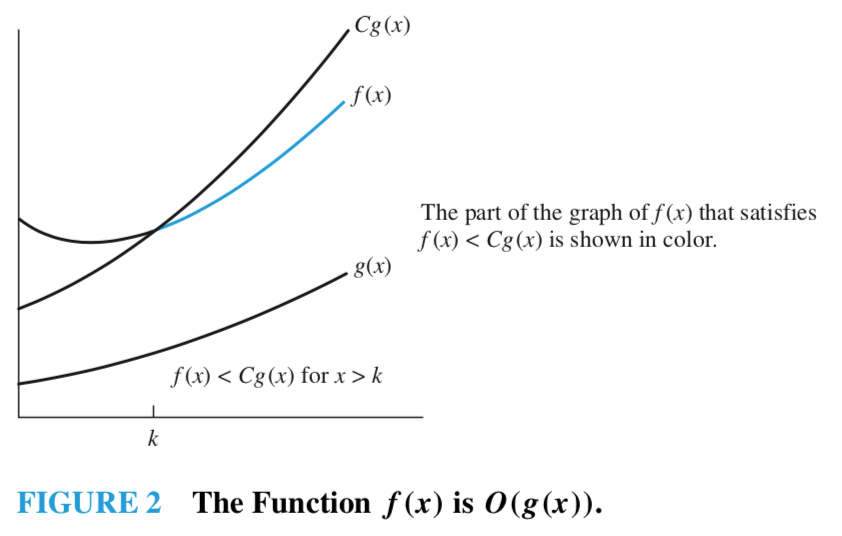
Definition
Let ${f}$ and ${g}$ be functions from the set of integers or the set of real numbers to the set of real numbers. We say that ${f(x)}$ is ${O(g(x))}$ if there are constants ${C}$ and ${k}$ such that ${|f(x)| <= C|g(x)|}$
whenever ${x > k}$. This is read as "${f(x)}$ is big-oh of ${g(x)}$".

Big-O를 표기할 때 ${f(x)}$가 ${O(g(x))}$인 관계에 등장하는 함수 ${g}$는 가능한 한 작은 것을 선택해야 한다.

(출처 :https://johngrib.github.io/wiki/big-O-notation/)

---

컴퓨터에서 정렬을 수행하는 이유 중 가장 큰 이유가 바로 '이진탐색(binary search)'가 가능한 상태를 만들기 위함임.

실제 응용에서는 상황에 따라 2가지 이상의 정렬을 사용하는 경우가 많음.
아래부터는 정렬의 종류를 서술해봄.

O(${n^2}$) Algorithm

Bubble Sort

최대 ${n(n-1)/2}$ 번 정렬. 쓸모 없어서 굳이 안 써도 될 듯.
T(n) = ${n(n-1)/2}$, therefore O(n) = ${n^2}$

def bubble_sort(arr):
    for i in range(len(arr) - 1, 0, -1):
        for j in range(i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

Selection Sort

사람들이 실제로 정렬을 할 때 생각하는 sort 방법(모든 index에 대해 각 index에 위치시킬 값을 '선택'시키기 때문에 붙은 정렬 이름)
O(n) = ${n^2}$
(1) 배열이 작거나, (2) 정렬되어 있는 자료구조에 하나씩 삽입/제거할때는 효율적인 방법이라고 한다.

def selection_sort(arr):
    for i in range(len(arr) - 1):
        min_idx = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

O(${nlogn}$) Algorithm

Merge sort

"Devide and Conquer"
시간복잡도에 log(n)이 등장하는 경우는, "이진 검색" 행위를 할 때인 듯하다.(전화번호부가 있고, 어떤 사람의 이름이 주어지면, 책 중간 쯤에서 임의 지점을 선택하고 그 지점에 이름이 있는지 확인해나가면서 전화번호를 찾는 행위) 수학적으로 이 행위가 어떻게 logn something으로 근사되는지는 차차 공부해봐야할 듯함.

merge sort의 "Devide"에서 n->n/2->n/4->...->1를 거치면서 O(logn)의 시간(과정)이 필요하고, "Conquer" 시 O(n)의 시간이 필요함. 따라서 ${O(n)} = n log n$

 def merge_sort(arr):
    if len(arr) < 2:
        return arr

    mid = len(arr) // 2
    low_arr = merge_sort(arr[:mid])
    high_arr = merge_sort(arr[mid:])

    merged_arr = []
    l = h = 0
    while l < len(low_arr) and h < len(high_arr):
        if low_arr[l] < high_arr[h]:
            merged_arr.append(low_arr[l])
            l += 1
        else:
            merged_arr.append(high_arr[h])
            h += 1
    merged_arr += low_arr[l:]
    merged_arr += high_arr[h:]
    return merged_arr

Heap sort

"안정적"으로 ${O(nlogn)}$의 성능을 내는 알고리즘.
Heap tree를 이용한, selection sort랑 거의 비슷한 알고리즘이다. Heap은 주로 "큰 키(혹은 작은 키)"에 자주 액세스할 때 유용한 자료 구조이다. 생김새는 completely binary tree이며, root node가 최대값이냐, 최소값이냐에 따라 Max heap, Min heap 으로 나뉜다. heap에서 쓰이는 tree모양과 규칙이 binary search tree와 어떻게 다른지 인지해두는 것도, 훗날 목적성에 맞게 자료구조를 짜야할 때 도움이 될 것 같다. (아래 참고)

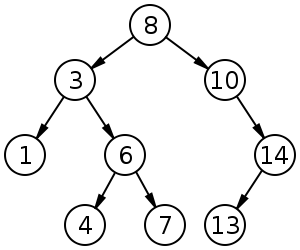
Heap vs Binary Search Tree
아래 그림은 이진탐색트리(Binary Search Tree)를 나타내고 있습니다. 힙과 이진탐색트리 모두 이진트리라는 점에서 공통점을 가지만 노드값이 다소 다르게 구성돼 있는 점을 확인할 수 있습니다. 힙은 각 노드의 값이 자식노드보다 큰 반면, 이진탐색트리는 왼쪽 자식노드가 제일 작고 부모노드가 그 다음 크며 오른쪽 자식노드가 가장 큰 값을 가집니다. 힙은 우선순위(키) 정렬에, 이진탐색트리는 탐색에 강점을 지닌 자료구조라고 합니다.

출처 : https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/

heap 성질을 만족하도록 하는 연산을 heapify라고 한다.
max heap의 heapify 관련 recursion python code는 아래와 같다.(이렇게 쓰고 보니, ratsgo님 아티클만큼 heap sort를 잘 정리한 한글 문서가 없다;)

def heapify(unsorted, index, heap_size):
    largest = index
    left_index = 2 * index + 1
    right_index = 2 * index + 2
    # 물론 largest 값이 오른쪽 자식 노드보다도 작을 수 있지만, 알고리즘 구현상 왼쪽 우선 적용
    # 어쨌든 오른쪽, 왼쪽 자식 노드들 중에 큰 놈을 위로 올리는 if문 2개
    if left_index < heap_size and unsorted[left_index] > unsorted[largest]:
        largest = left_index
    if right_index < heap_size and unsorted[right_index] > unsorted[largest]:
        largest = right_index
    #오른쪽, 왼쪽 자식 노드와 index(largest였던) 노드를 비교해서, 자식 노드들이 더 크다면, heap tree 상에서 위치를 바꿔주는 if 구문
    if largest != index:
        unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest]
        return heapify(unsorted, largest, heap_size)

또한 아래는 heap sort python code이다. heapify를 참고해서 고민해보면 좋을 듯하다.

힙 정렬의 수행방식은,

• 주어진 원소들로 max(or min) heap을 구성한다.
• heap의 루트노드와 말단노드를 교환해준다.
• 새 루트노드에 대해 max(or min) heap을 구성한다.
• 원소 개수만큼 위 두 단계의 과정을 반복한다.

def heap_sort(unsorted):
    n = len(unsorted)
    # BUILD-MAX-HEAP (A) : 위의 1단계
    # 인덱스 : (n을 2로 나눈 몫-1)~0
    # 최초 힙 구성시 배열의 중간부터 시작하면 
    # 이진트리 성질에 의해 모든 요소값을 
    # 서로 한번씩 비교할 수 있게 됨 : O(n)
    for i in range(n // 2 - 1, -1, -1):
        heapify(unsorted, i, n)
    # Recurrent (B) : 2~4단계
    # 한번 힙이 구성되면 개별 노드는
    # 최악의 경우에도 트리의 높이(logn)
    # 만큼의 자리 이동을 하게 됨
    # 이런 노드들이 n개 있으므로 : O(nlogn)
    for i in range(n - 1, 0, -1):
        unsorted[0], unsorted[i] = unsorted[i], unsorted[0]
        heapify(unsorted, 0, i)
    return unsorted

정리하면, heap을 구성하고, 가장 큰 원소(or 작은 원소)를 빼내고, 나머지 것들로 다시 heap을 구성하고, 또 가장 큰 원소(or 작은 원소)를 빼내는 구조.
(출처: https://leedakyeong.tistory.com/entry/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%ED%8C%8C%EC%9D%B4%EC%8D%AC%EC%9C%BC%EB%A1%9C-%ED%9E%99-%EC%A0%95%EB%A0%AC-%EA%B5%AC%ED%98%84%ED%95%98%EA%B8%B0-heap-sort-in-python)

Quick sort

임의의 pivot을 잡고 정렬하는 devide and conquer&recursion 알고리즘.

이건 너무 좋은 소스가 있어서 공유한다.
(출처: https://www.daleseo.com/sort-quick/)

위 출처에서 따온 메모리 최적화된 quick sort python code는 아래와 같다.

def quick_sort(arr):
    def sort(low, high):
        if high <= low:
            return

        mid = partition(low, high)
        sort(low, mid - 1)
        sort(mid, high)

    def partition(low, high):
        pivot = arr[(low + high) // 2] #low, high는 시작 인덱스, 끝 인덱스
        while low <= high:
            while arr[low] < pivot: # while 문을 나설때는 pivot보다 큰 값을 왼쪽에서 찾았을때
                low += 1
            while arr[high] > pivot:
                high -= 1
            if low <= high: # 이 if문에 닿을 때면, 위 2개의 while문에서 왼쪽, 오른쪽 swap할 값을 찾았을 때임.
                arr[low], arr[high] = arr[high], arr[low]
                low, high = low + 1, high - 1 #while구문 안에 low +=1, high -=1을 적용 받지 못했으므로 넣어줌.
        return low # 다음 재귀호출의 분할 기준점(pivot)이 될 시작 인덱스를 리턴하는 것!

    return sort(0, len(arr) - 1)