지도학습

답까지 나온 데이터를 많이 주어서 학습시킨 후 새로운 문제에 대한 답을 얻는 방법이다.

KNeighborsClassifier

KNeighborsRegressor

LinearRegression

LogisticRegression, LinearSVC

KNN 알고리즘 (최근접 알고리즘)

K Nearest Neighbor : 주변의 데이터를 살펴본 뒤 더 많은 데이터가 포함되어 있는 범주로 분류하는것

mglearn.plots.plot_knn_classification(n_neighbors=1)

n_neighbors=3이면 주변의 3개, =6이면 6개 but 홀수단위로 하는것이 좋음

mglearn 외부 시각화 모듈, 분석에서의 복잡한 시각화 함수를 제공함

주피터 환경(아나콘다)에서는 !가 붙음
!pip install mglearn 

matplotib : 시각화 모듈

X, y = mglearn.datasets.make_forge() #인위적으로 만든 이진분류 
mglearn.discrete_scatter(X[:,0], X[:,1], y)

scatter 산포도
discrete 이산

plt.legend 범례출력

X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=0)

train_test_split : X와 y로 train데이터와 test데이터를 분리하는다.

random_state=0 호출할 때마다 같은 학습 테스트용 데이터 세트를 생성하기 위해 주어지는 난수 발생값, 어떤값이든 상관없음
+train:test = 80:20 이지만, 100까지의 숫자로 했을때 train데이터가 1~80일지 21~100일지에 따라 당연히 데이터가 달라짐
=> 그래서 scikit learn에서 사용하는 random_state 인자는 수행시마다 동일한 결과를 얻기 위해 적용합니다.

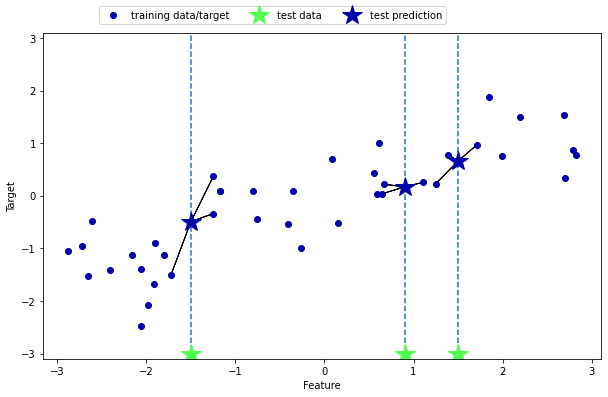
KNeighborsClasifier knn알고리즘분석기
.fit : 모델학습시키는 메소드, KNN이 테스트셋을 분류할 때 이웃을 찾을 수 있도록 데이터를 저장 trainX,y
.predict : 확률 리스트로 반환해서 예측해보는 것 testX만
---------(testy는 정답이니까 정답을 넣어서 예측하는것은 말이 안된다)
.score : 테스트 데이터와 테스트 레이블을 넣어 정확도 출력

★ Linear Regression에서 fit() vs predict()

 fit(trainX,trainy) -> predict(testX)

linear_regression 선형 회귀
답까지 나온 데이터를 많이 주어서 학습시킨 후 새로운 문제에 대한 답을 선형 모델로 얻는 방법이다.

fig,axes = plt.subplots(1,3,figsize=(10,3)) 
#값이 fig와 축에 리턴된다 
#subplot: 한라인에 그림 여러개 그릴수있음 plot은 그냥 그리는것
#fig =figure 
# axes 축 axis 중심축
for n_neighbors, ax in zip([1,3,9], axes):
    # KNN 모델 생성
    clf = KNeighborsClassifier(n_neighbors = n_neighbors).fit(X, y)
    # KNN 결정 경계
    mglearn.plots.plot_2d_separator(clf ,X ,fill=True, eps=0.5, ax=ax alpha=0.4)
    # 산점도
    mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)

eps : 점으로 부터의 반경
alpha: 제약거는 것

zip(*iterable)은 동일한 개수로 이루어진 자료형을 묶어 주는 역할을 하는 함수이다.

※ 여기서 사용한 *iterable은 반복 가능(iterable)한 자료형 여러 개를 입력할 수 있다는 의미이다.

잘 이해되지 않는다면 다음 예제를 살펴보자.

 list(zip([1, 2, 3], [4, 5, 6]))
		[(1, 4), (2, 5), (3, 6)]
 list(zip([1, 2, 3], [4, 5, 6], [7, 8, 9]))
		[(1, 4, 7), (2, 5, 8), (3, 6, 9)]
 list(zip("abc", "def"))
		[('a', 'd'), ('b', 'e'), ('c', 'f')]

train 데이터 : 내가 준대로 잘했냐?

test 데이터 : test 데이터로 검사할게 // 이쪽이 중요

학습 데이터 정확도는 떨어지는 경향
테스트 데이터 정확도는 비슷하게 유지하는 경향, 이 둘이 비슷하게 나오는 정확도가 가장 이상적인 순간

shape(a,b) a x b 차원의 예제 배열로 만드는것
np.arrange(12).reshape(3,4) 면
([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
reshape() : shape를 재지정하는 느낌

하지만 reshape(-1,정수)의 경우
열 차원의 정수에 따라서 전체갯수의 원소가 빠짐없이 배치될 수 있도록 -1이 들어가 있는 행의 갯수를
'가변적'으로 정하는 것
reshape(-1,1) => shape(12,1)
reshape(-1,2) => shape(6,2)
reshape(-1,3) => shape(4,3)

Reshape의 내용 https://rfriend.tistory.com/345

.linespace(start,stop,num,endpoint,restep) ex) linespace(0,1,6)
범위내에서 주어진 sample의 갯수만큼 생성
output = [0. ,0.2, 0.4, 0.6, 0.8, 1.]

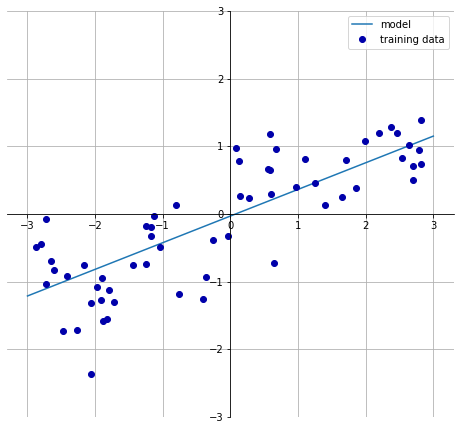
X, y = mglearn.datasets.make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)

lr = LinearRegression().fit(X_train, y_train)
print(lr.coef_) #가중치, 기울기
print(lr.intercept_) #편향, 절편

Ridge 릿지 : 제약을 거는 것

LinearRegression().fit(X_train, y_train).score(X_train, y_train)
= 학습정확도는 높은데 테스트정확도는 낮음
Ridge().fit(X_train, y_train).score(X_train, y_train)
= 학습정확도는 낮은데 테스트 정확도는 높음
(맞는 문법임)

-alpha는 제약값, 학습량에 제약을 거는것
예) Ridge(alpha=10).fit(X_train, y_train)
---값이 클수록 모델의 구조 단순해짐=>모델의 성능 낮아지지만 일반화 but 과소적합 위험성
---작으면 모델의 복잡도 상승 = > 학습성능 좋지만 과대적합 위험성
---0이면 제한없이 학습하는 것

Lasso 라쏘, 회귀 알고리즘의 하나

alpha 값이 낮을수록 정확도가 오름

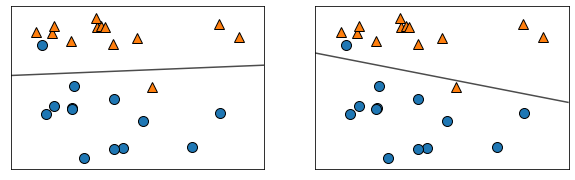
LogisticRegression, LinearSVC

eps : 점으로 부터의 반경

데이터=> 분류: classification 이나 clustor
	 => 값 : regression -> 관련 알고리즘

경사 하강법