1.학습한 내용

1)mglearn

안드레아스 뮐러 가 자주 사용한 라이브러리를 사용하여 수업을 진행하게 되었다.

기본적인 라이브러리들을 불러온다.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

mglearn 을 import 하기위해서 우선 mglearn을 설치한다.

!pip install mglearn

그리고 mglearn 을 import한다.

import mglearn

이때 mglearn은 데이터를 만들어주고 그리는 역할을 한다.

이를 통해서 mglearn 의 명령어중 하나를 사용하여 데이터를 생성하고, 그를 시각화하는 그래프를 만든다.

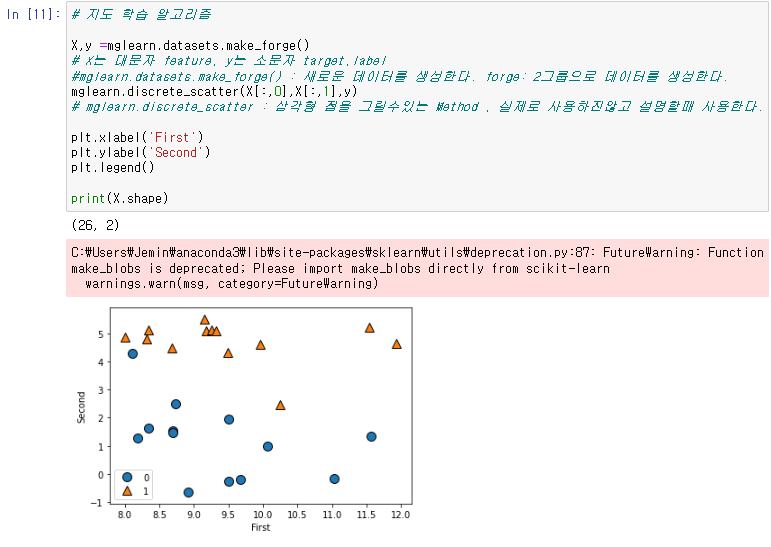
X,y =mglearn.datasets.make_forge()
mglearn.discrete_scatter(X[:,0],X[:,1],y)

plt.xlabel('First')
plt.ylabel('Second')
plt.legend()

이때 forge 는 2그룹의 데이터를 생성한다는 의미를 가진다.

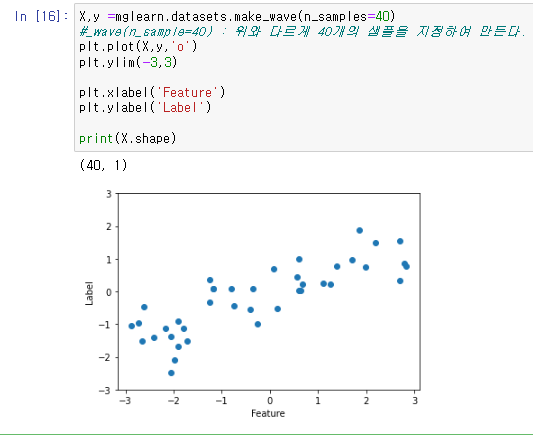
forge 와 다르게 wave를 사용하여 데이터를 만들수도있다.

X,y =mglearn.datasets.make_wave(n_samples=40)

plt.plot(X,y,'o')
plt.ylim(-3,3)

plt.xlabel('Feature')
plt.ylabel('Label')

1-1)최근접 알고리즘 Classification

mglearn 에서는 이전에 배웠던 최근접 알고리즘을 표시하여 보여주는것 또한 가능하다.

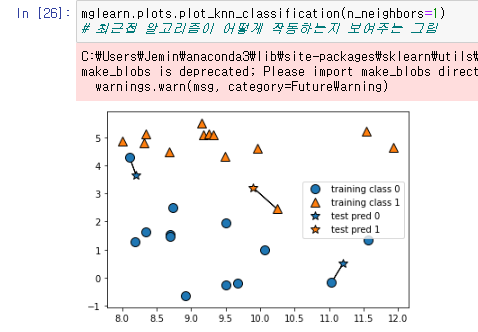
mglearn.plots.plot_knn_classification(n_neighbors=1)

를 통하여 기준점이 1개일때의 최근접 알고리즘을.

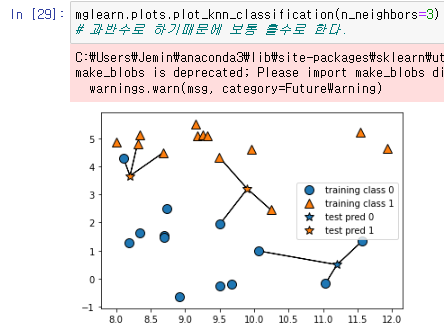
mglearn.plots.plot_knn_classification(n_neighbors=3)

를 통하여 기준점이 3개일때의 최근접 알고리즘을 볼수있는데.

사진과 같이 최근접 알고리즘은 기준점을 몇개로 설정하느냐에 따라서 결과값이 다르게 나올수있다는것을 알수있다.

이를 통해서 학습용, 테스트용 데이터를 통해서 데이터를 쪼개서 테스트를 하게 될것이다.

이를 위해서 데이터를 분류하기 위한 라이브러리를 불러온다.

from sklearn.model_selection import train_test_split

그리고 분류할 데이터로 mglearn 을 사용하여 만든 후, 분류를 한다.

X,y = mglearn.datasets.make_forge()

X_train, X_test ,y_train , y_test= train_test_split(X,y,random_state=0)

이제 최근접 알고리즘을 사용하기 위해서 최근접 알고리즘 라이브러리를 불러온다.

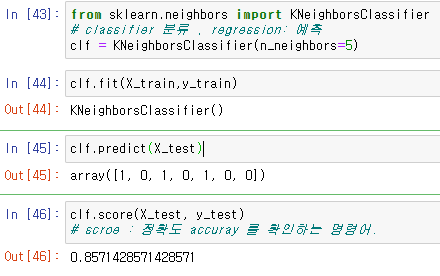
from sklearn.neighbors import KNeighborsClassifier

clf = KNeighborsClassifier(n_neighbors=5)

이후 이 classifier 에 훈련데이터를 넣고 테스트를 진행하고, 그 정확도를 측정한다.

clf.fit(X_train,y_train)
clf.predict(X_test)

clf.score(X_test, y_test)

이제 최근접 알고리즘을 진행할때 기준점의 갯수가 얼마나 영향을 주는지를 확인하기 위해서, 그래프를 동시에 보면서 비교를 하는것을 진행한다.

fig, axes= plt.subplots(1,3,figsize=(10,3))

for n_neighbors, ax in zip([1,3,9],axes):
    clf= KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X,y)
    
    mglearn.plots.plot_2d_separator(clf,X,fill=True,eps=0.5, ax=ax,
                                   alpha=0.4)
    mglearn.discrete_scatter(X[:,0],X[:,1], y,ax=ax)

이 코드를 통해서 기준점이 1개일때와 3개일때, 그리고 9개일때에 따라서 범위가 달라지는것을 알수있다.

이제 이를 통해서 기준점에 따른 정확도 accuracy 에 대해서 정의를 한다

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()

X_train,X_test,y_train,y_test =train_test_split(
    cancer.data,cancer.target,random_state=66
)

training_accuracy=[]
test_accuracy =[]

이후 기준점의 갯수를 뜻하는 리스트를 만들고.
그 기준점 마다의 데이터값을 만든다.

neighbors_settings = range(1,11)
for n_neighbors in neighbors_settings:
    clf = KNeighborsClassifier(n_neighbors=n_neighbors)
    clf.fit(X_train,y_train)
    
    training_accuracy.append(clf.score(X_train,y_train)) 
    test_accuracy.append(clf.score(X_test,y_test))

이제 이렇게 만들어진 데이터값들을 이용해서 그래프를 만드는 것으로
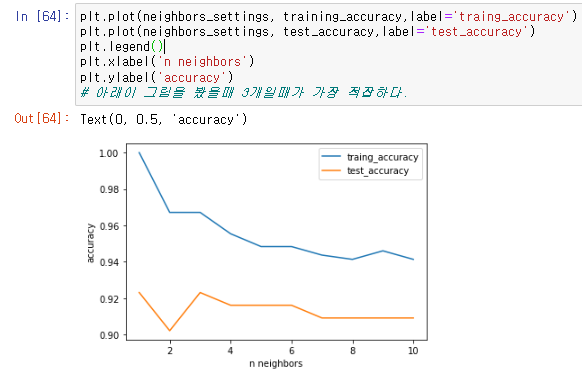
기준점에 따라서 traing 데이터와 test 데이터의 정확도를 보여주는 그래프를 그린다.

plt.plot(neighbors_settings, training_accuracy,label='traing_accuracy')
plt.plot(neighbors_settings, test_accuracy,label='test_accuracy')
plt.legend()
plt.xlabel('n neighbors')
plt.ylabel('accuracy')

정확도를 사용할때 중요한것은 test_accuracy 인데, 이때 가장 적합한 기준점의 갯수는 3개라는것을 그래프를 통해 알수있다.

1-2)최근접 알고리즘 Regression

mglaern 을 이용하면 classification 분류만 가능한것이 아니라 Regression 또한 가능하다.

mglearn.plots.plot_knn_regression(n_neighbors=1)

위는 기준점이 1개 일때 이고,

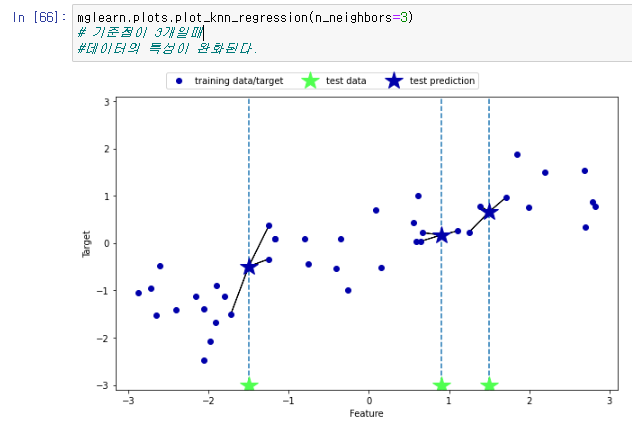
mglearn.plots.plot_knn_regression(n_neighbors=3)

이것은 기준점이 3개 일때 이며 이것은

사진과 같이 바뀌는것을 확인할수있다.

이제 최근접 알고리즘으로 Regression 을 하기 위해서 라이브러리를 불러와서 테스트를 통하여 데이터를 생성한다.

from sklearn.neighbors import KNeighborsRegressor


X,y = mglearn.datasets.make_wave(n_samples=40)

X_train,X_test,y_train,y_test =train_test_split(X,y,random_state=0)

reg = KNeighborsRegressor(n_neighbors=3)
reg.fit(X_train,y_train)

이 테스트를 한 데이터를 바탕으로 classification 을 했던것 처럼 subplot 을 만들어서 시각화하여 비교를 한다.

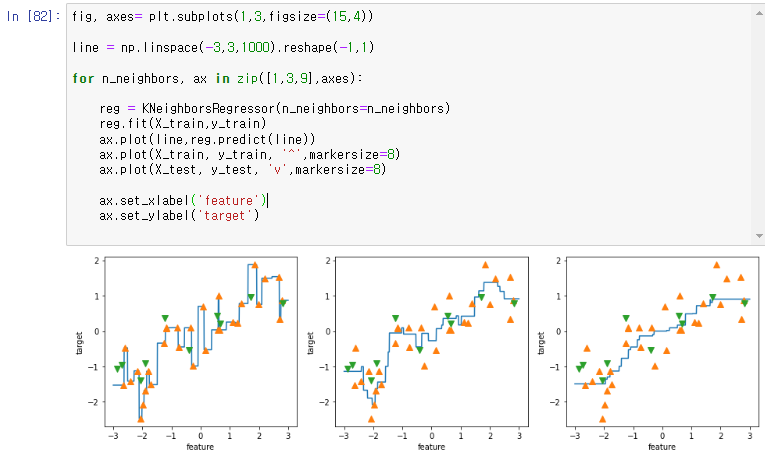
fig, axes= plt.subplots(1,3,figsize=(15,4))

line = np.linspace(-3,3,1000).reshape(-1,1)
                               
for n_neighbors, ax in zip([1,3,9],axes):
    
    reg = KNeighborsRegressor(n_neighbors=n_neighbors)
    reg.fit(X_train,y_train)
    ax.plot(line,reg.predict(line))
    ax.plot(X_train, y_train, '^',markersize=8)
    ax.plot(X_test, y_test, 'v',markersize=8)
    
    ax.set_xlabel('feature')
    ax.set_ylabel('target')

이를 통해서 기준점이 늘어날수록 완만해지는것을 볼수있으며, 또한 기준점이 너무 많아지면 변별력이 떨어지는것 또한 확인할수 있다.

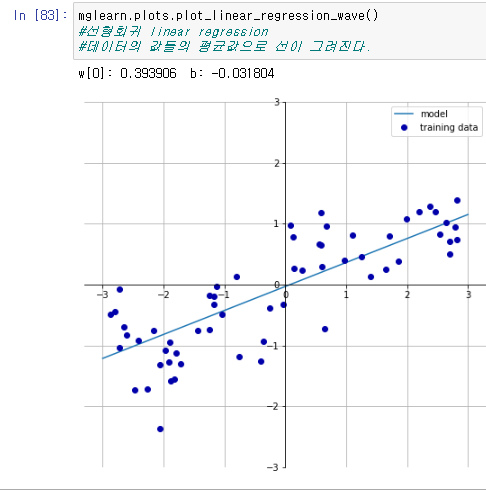
2)Linear Regression 선형회귀

데이터값들의 평균값으로 직선을 그리는 그래프로
이 또한 mglearn 에서 사용이 가능하다.

mglearn.plots.plot_linear_regression_wave()

이를 또한 기존의 라이브러리를 통하여 표현이 가능한데. 우선 라이브러리를 불러온다.

from sklearn.linear_model import LinearRegression

X , y = mglearn.datasets.make_wave(n_samples=60)

X_train, X_test, y_train, y_test = train_test_split(X,y,random_state=42)

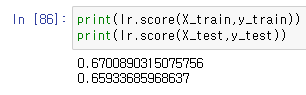
lr = LinearRegression().fit(X_train,y_train)

이를 통해서 정확도를 확인할수도 있다.

print(lr.score(X_train,y_train))
print(lr.score(X_test,y_test))

이때 기울기와 y절편을 구하는 코드 coef 와 intercept 를 사용한다.

print(lr.coef_)
print(lr.intercept_)

이때 나오는 값인 기울기와 절편이 위에서 mglearn 을 통해서 그린 선형회귀 그래프의 기울기와 절편과 같다는것을 확인할수있다.

2-1) Ridge Regression 릿지

기존의 최근접 알고리즘에서는 기준점의 갯수를 조절하는것으로 가중치와 편향을 알 수 있었던데에 비해서 선형회귀에서는 가중치와 편향을 찾기 어렵다는 단점을 가지고 있어서 , 그를 해결하기 위해서 생긴것이 릿지,라쏘 이다.

우선 릿지를 라이브러리에서 불러온 뒤, 그대로 사용했을때의 정확도를 확인한다.

from sklearn.linear_model import Ridge

ridge = Ridge().fit(X_train,y_train)

print(ridge.score(X_train,y_train))
print(ridge.score(X_test,y_test))

알고리즘을 바꾸니 기존의 선형회귀보다 테스트의 정확도가 올라간것을 확인할수있다.

이제 릿지를 사용하게 된 이유중 하나인 가중치,제약을 걸도록 한다, 이때 제약은 alpha로 지정한다.

ridge10 = Ridge(alpha=10).fit(X_train,y_train)

print(ridge10.score(X_train,y_train))
print(ridge10.score(X_test,y_test))

제약을 주니 정확도가 기존보다 낮아진것을 볼수 있었고 반대로.

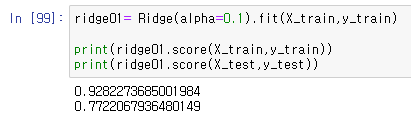
ridge01= Ridge(alpha=0.1).fit(X_train,y_train)

print(ridge01.score(X_train,y_train))
print(ridge01.score(X_test,y_test))

제약을 적게 줬을때, 정확도가 더 올라간것을 확인할수 있었다.
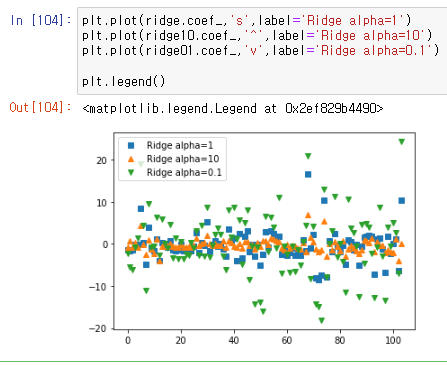
이를 시각적으로 보기 위해서 그래프를 그리게되면

plt.plot(ridge.coef_,'s',label='Ridge alpha=1')
plt.plot(ridge10.coef_,'^',label='Ridge alpha=10')
plt.plot(ridge01.coef_,'v',label='Ridge alpha=0.1')

plt.legend()

기준이 되는 기본값 파랑색상자가 분포가 되어있는데,
높은 제약이 걸린 alpha=10 일때는 중앙으로 데이터들이 모인것을 확인할수 있었고.
낮은 제약이 걸린 alpha=0.1 일때는 데이터가 기존보다 더 넓게 분포된것을 확인할수있다.

2-2) Lasso Regression 라쏘

라쏘 화귀를 확인하기 위해서 라이브러리에서 불러온 뒤 그대로 사용했을때의 정확도를 측정한다.

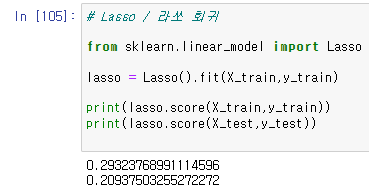
from sklearn.linear_model import Lasso

lasso = Lasso().fit(X_train,y_train)

print(lasso.score(X_train,y_train))
print(lasso.score(X_test,y_test))

이때는 기존의 선형회귀보다 정확도가 더 떨어진것을 확인할수있다.

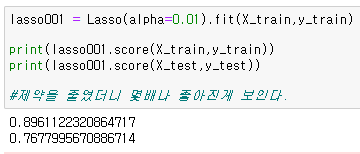
이를 통해서 가중치를 0.01을 설정을 한다.

lasso001 = Lasso(alpha=0.01).fit(X_train,y_train)

print(lasso001.score(X_train,y_train))
print(lasso001.score(X_test,y_test))

제약을 적게 넣으니 정확도가 몇배나 좋아진것을 확인 할수 있었다.
이를 통해서 제약을 더 적게 넣으면 어떻게 되는지를 확인 하기 위해서 제약을 0.0001 을 넣게되면

lasso00001 = Lasso(alpha=0.0001).fit(X_train,y_train)

print(lasso00001.score(X_train,y_train))
print(lasso00001.score(X_test,y_test))

제약을 0.01을 넣었을때에 비해서 학습데이터의 정확도는 올라 갔지만, 테스트데이터는 오히려 정확도가 낮아진것을 확인할수있었다.

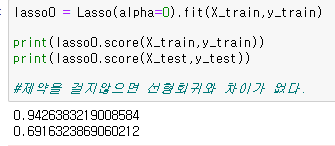
이를 통해서 오히려 제약을 안넣게 되면 어떻게 되는지를 확인하였다.

lasso0 = Lasso(alpha=0).fit(X_train,y_train)

print(lasso0.score(X_train,y_train))
print(lasso0.score(X_test,y_test))

이때는 오히려 기존에 확인했던 선형회귀의 정확도와 같은것을 확인할수 있었다.

이를 통해서 제약을 거는것에서도 테스트데이터의 정확도가 높은것을 찾는것이 중요하다는것을 알수있다.

3) 분류에 대한 선형 모델

선으로 인해서 분류를 하는것이며, 이 또한 라이브러리에 존재하므로 그를 불러온다.

from sklearn.linear_model import LogisticRegression

from sklearn.svm import LinearSVC

이때 LogisticRegression 으로 Regression 이지만 회귀가 아닌 분류 알고리즘이다.

이를 통해 그림을 그리게 되면

X,y = mglearn.datasets.make_forge()

fig,axes = plt.subplots(1,2,figsize=(10,3))

for model, ax in zip([LinearSVC(),LogisticRegression()],axes):
    clf = model.fit(X,y)
    
    mglearn.plots.plot_2d_separator(clf,X,fill=False,eps=0.5,alpha=0.7,ax=ax)
    
    mglearn.discrete_scatter(X[:,0],X[:,1],y,ax=ax)

그리고 이러한 그림그리기 또한 mglearn 에서 보여주는 것으로 이미 존재한다.

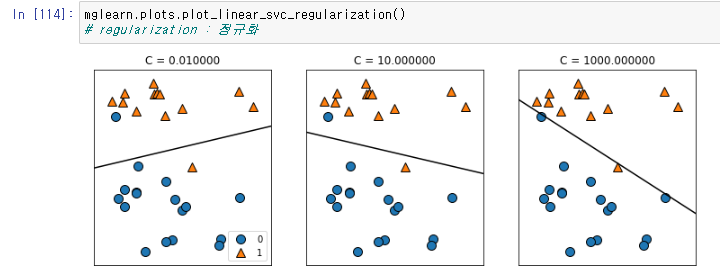
mglearn.plots.plot_linear_svc_regularization()

이를 통하여 선형분류, 정규화가 가능하다.

이러한 선형분류를 통해서
이 선형분류의 정확도를 측정한다.
이를 위해서 유방암 데이터셋을 가져온뒤 분류하고, 그를 통해서 선형분류를 진행한다.

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train,X_test,y_train,y_test = train_test_split(cancer.data,cancer.target,random_state=42)

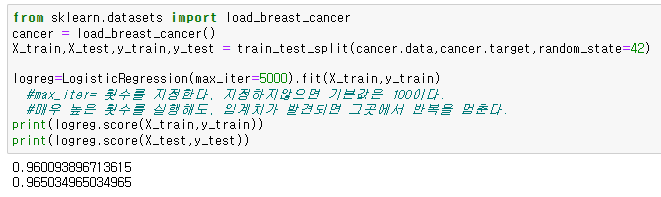
logreg=LogisticRegression(max_iter=5000).fit(X_train,y_train)

print(logreg.score(X_train,y_train))
print(logreg.score(X_test,y_test))

이를 통해서 상당히 높은 정확도를 가지는것을 확인할수 있다.
이때 횟수를 5천으로 설정했지만, 실제로는 5천번의 실행을 전부 다 하는것이 아니라, 실행을 반복하던 도중 임계점에 닿게되면 그때는 실행을 끝내기 때문에 빠르게 결과가 나온다.

2.학습내용 중 어려웠던 점

이미 짜여진 코드들을 읽고 이해 하는것에 어려움을 겪었다.
mglearn.

3.해결방법

이번 수업에서는 mglearn 이 작동하는것을 보여주고 그것이 어떤 식의 코드들이 작동해서 나온것인지를 알고리즘을 통하여 내용들을 새로 짜면서 하는것으로 확인할수있었다.

4.학습소감

제대로 배웠다고 생각했던 부분들이 이번 수업에서 잘못 배웠었다는것들 깨닫게 되었다, 예를 들어 최근접 알고리즘의 경우 각 섹션에서의 점들을 기준으로 갯수를 세는 것으로 생각했었다, 예를 들어서 n_neighbors=3 이고 섹션이 2개가 있을때 1번섹션에서의 점 3개에서 입력한값의 거리의 평균과, 2번섹션에서의 점 3개에서의 입력한값의 거리의 평균을 비교하여서 알맞은 섹션에 데이터가 입력이 되는줄 알았는데, 그저 입력한 값의 위치에서 섹션을 구분하지 않고 가장 가까운 점 3개를 선택하고, 그중에 더 많은 갯수를 가진 지점의 데이터값이 된다는것을 오늘 mglearn 의 최근접 알고리즘을 보여주는 그림을 통해서 알게 되었다.
앞으로도 잘못 이해하고 있을수 있었던 것을 올바르게 배울수 있게 되어서 알찬 시간이었다고 생각한다.