CS224N Lecture 3

Named Entity Recognition(NER)

NER : find and classify names in text

possible uses :

Tracking mentions of particular entities in documents

For question answering, answers are usually named entities.

Simple NER : Widow classification using binary logistic classifier

idea : window의 주변 단어로부터 center word의 entity를 classify하는것

Train logistic classifier on hand-labeled data to classify center word {yes/no} for each class based on a concatenation of word vectors in a window

hand-labeled : center word가 어떤 entity인지를 레이블해둔것이다.

To classify all words: run classifier for each class on the vector centered on each word in the sentence

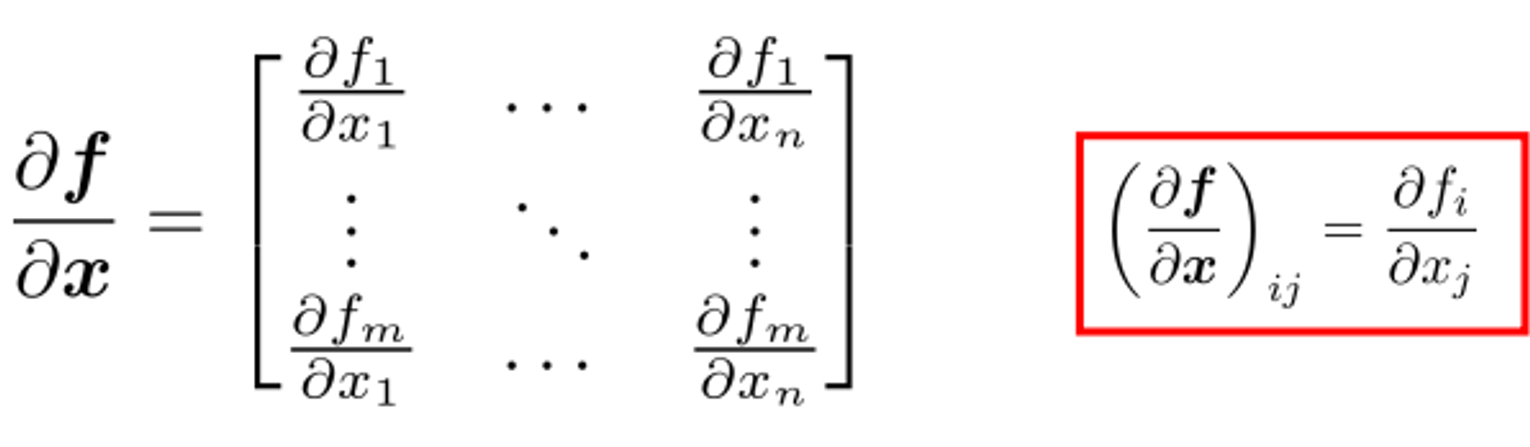
Jacobian Matrix

if $f(x)$ is a function $\mathbb{R}^n \rightarrow \mathbb{R}^m$

then $f(x) = [f_1(x_1,x_2,…,x_n),…,f_m(x_1,x_2,…,x_n)]$

than Jacobian matrix is

Elementwise activation Function

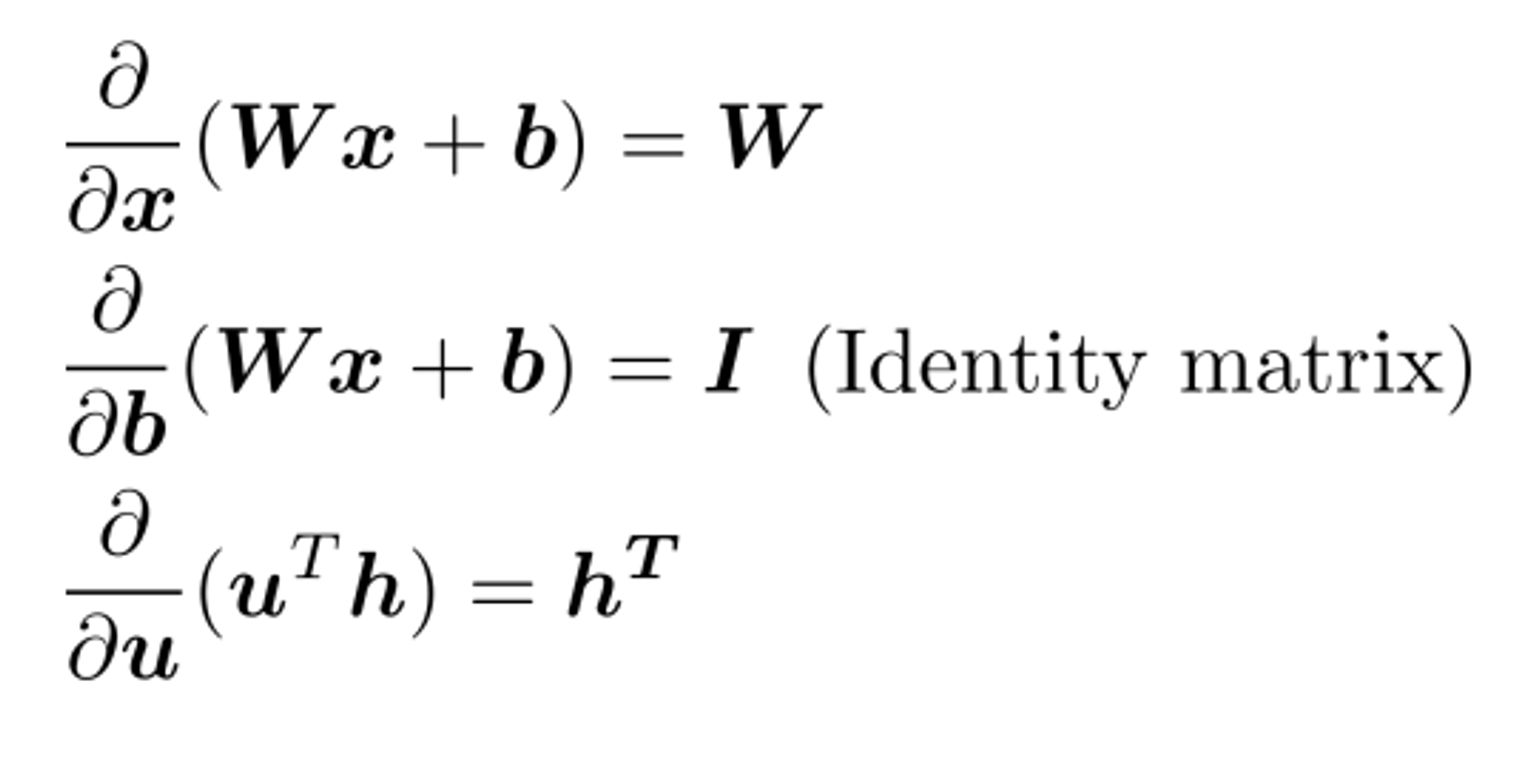
여기서

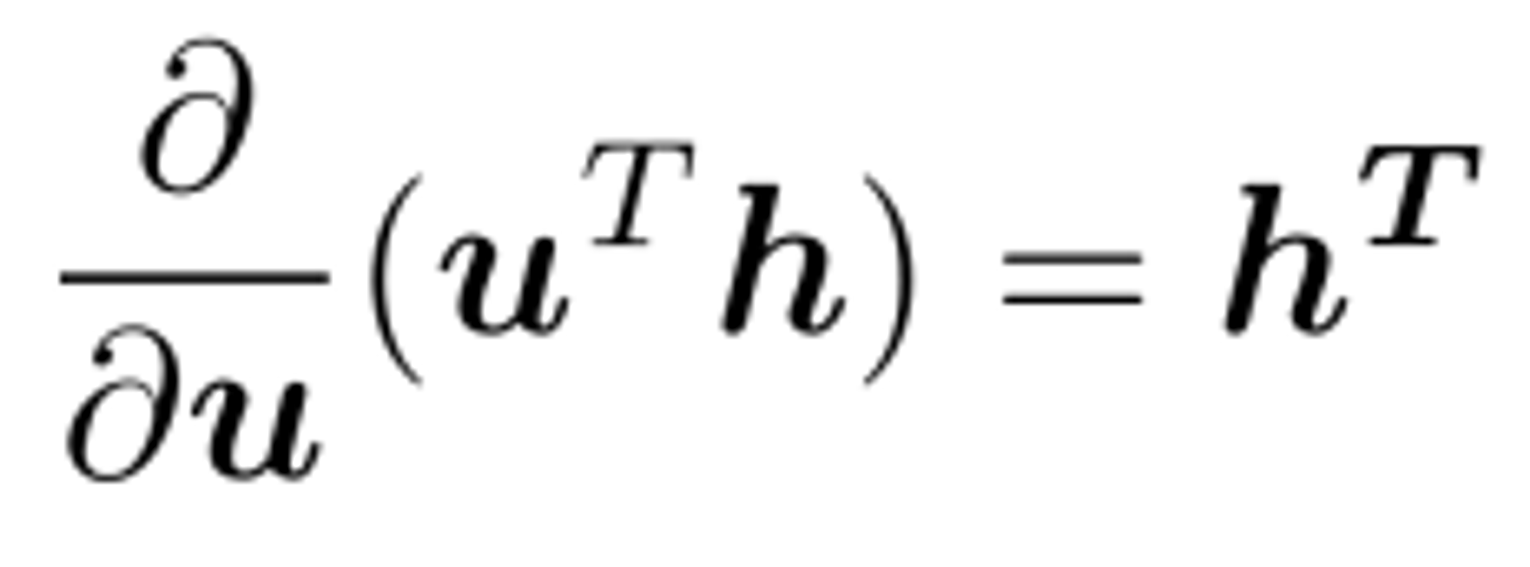
이걸 짚고 가자면,

$\frac{\partial}{\partial u_i}(\sum^n_{k = 1}u_kh_k) = h_i$

$\frac{\partial}{\partial u} (u^T h) = \begin{bmatrix} h_1 \\ h_2 \\ \vdots \\ h_n \end{bmatrix} = h$ 이어야 하는데 (u가 column vector이므로 scalar을 u로 미분하면 column vector가 나와야함) 계산상의 편의로 $h^T$로 설정한다.

(이러한 경우가 ML에서 상당히 많다고 한다.... 이거 때문에 애먹었는데..)

Backprop

$\frac{\partial s}{\partial W} = \delta \frac{\partial z}{\partial W} = \delta \frac{\partial}{\partial W}(Wx + b) = \delta ^Tx^T$

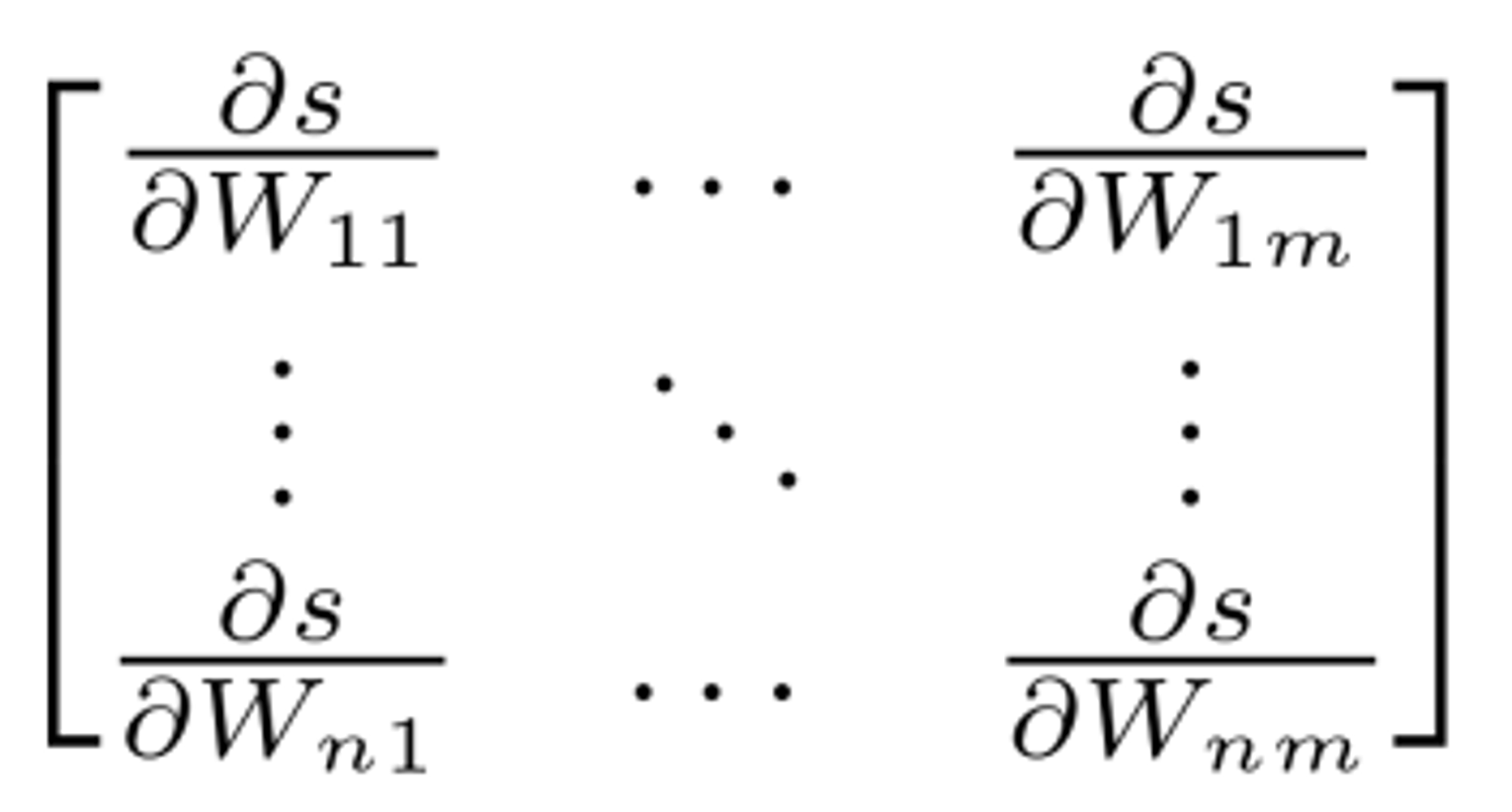
$z_i$의$z$$W_{ij}$에 대한 미분에 대해 생각해보자.

예를 들어 $W_{23}$은 $z_2$만을 미분할 수 있고, i = 2가 아닌 모든 i에 대해 $z_i$값에 대한 미분은 0이 된다.

따라서

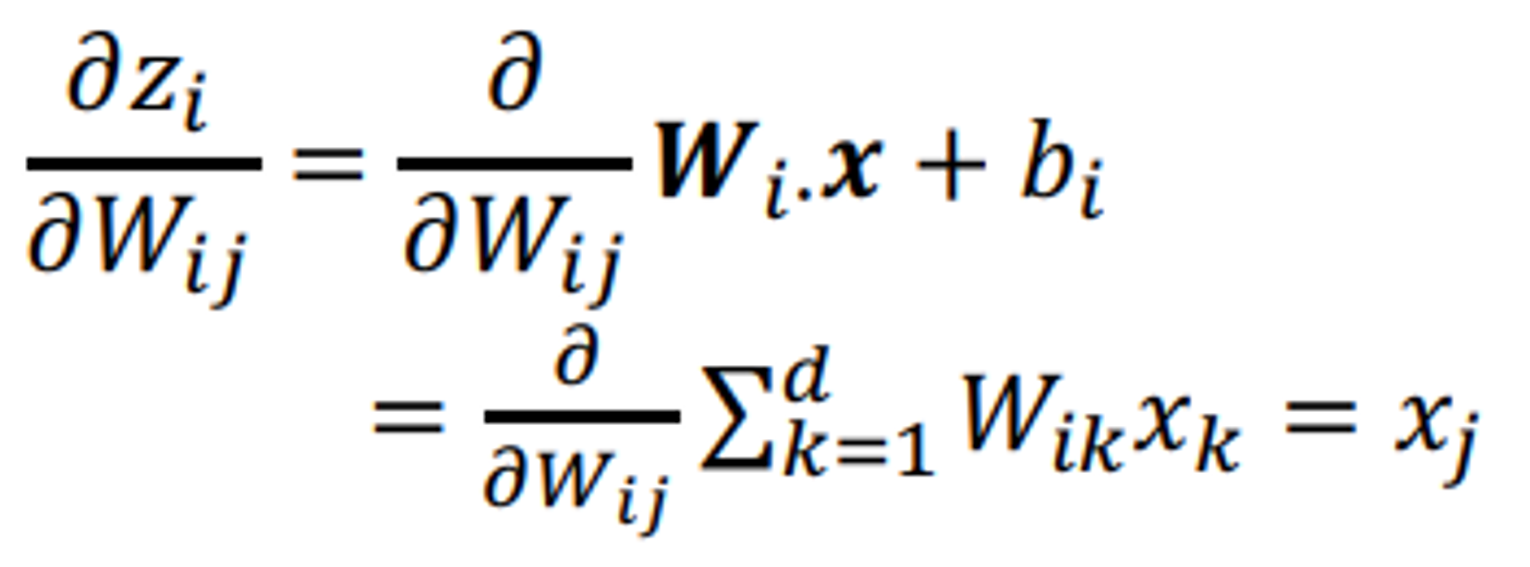
가된다.