Logistic Regression & Linear Regression

Regression(회귀)란 변수 두 개가 주어졌을 때, 한 변수에서 다른 변수를 예측하거나 두 변수의 관계를 규명하는 데 사용하는 방법이다. 이때 사용되는 변수의 유형은 다음과 같다.

• 독립 변수(예측 변수) : 영향을 미칠 것으로 예상되는 변수
• 종속 변수(기준 변수) : 영향을 받을 것으로 예상되는 변수

이때 두 변수 간 관계에서 돌깁 변수와 종속 변수의 설정은 논리적인 타당성이 있어야 한다. 예를 들어 몸무게(종속 변수)와 키(독립 변수)는 둘 간의 관계를 규명하는 용도로 사용된다.

Logistic Regression

왜 사용할까? : 주어진 데이터에 대한 분류
언제 사용할까? : 로지스틱 회귀 분석은 주어진 데이터에 대한 확신이 없거나 (예를 들어 분류결과에 확신이 없을 때) 향후 추가적으로 훈련 데이터 셋을 수집하여 모델을 훈련시킬 수 있는 환경에서 사용하면 유용하다.

Ligistic regression은 분석하고자 하는 대상들이 두 집단 혹은 그 이상의 집단으로 나누어진 경우, 개별 관측치들이 어느 집단으로 분류될 수 있는지 분류하고 이를 예측하는 모형을 개발하는 데 사용되는 통계 기법이다. 따라서 일반 회귀 분석과는 차이가 있다.

Logistic regression의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것이다. 이는 독립 변수의 선형 결합으로 종속 변수를 설명한다는 관점에서는 선형 회귀 분석과 유사하다. 하지만 로지스틱 회귀는 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 classification 기법으로 볼 수도 있다.

흔히 logistic regression은 종속 변수가 이항형 문제를 지칭할 때 사용된다. 이 외에, 두 개 이상의 범주를 가지는 문제가 대상인 경우엔 다항 로지스틱 회귀(multinomial logistic regression) 또는 분화 로지스틱 회귀 (polytomous logisitic regression)라고 하고, 복수의 범주이면서 순서가 존재하면 서수 로지스틱 회귀(ordinal logistic regression)라고 한다.

Mean Squared & Maximum Likelihood

최소 제곱법(mean squared)과 최대 우도법(maximum likelihood)은 랜덤 표본에서 모집단 모수를 추정하는데 사용한다. 최소 제곱법은 일반적인 회귀분석에서 사용하지만, 최대우도법은 로지스틱 회귀에서 사용한다.


최소 제곱법은 실제 갑에서 예측 값을 뺀 후 제곱해서 구할 수 있다.
$MSE=\frac{1}{n}\displaystyle\sum_{i=1}^n (y_i-\hat y_i)^2$
(사실 평균 제곱 오차임)


최대우도법을 설명하기 전에 먼저 우도에 대해 알아보자
우도(likelyhood, 가능도)는 나타난 결과에 따라 여러 가능한 가설을 평가할 수 있는 척도(measure)를 의미한다. 최대 우도는 나타난 결과에 해당하는 가설마다 계산된 우도 값 중 가장 큰 것을 의미한다. 즉 일어날 가능성(우도)이 가장 큰 것을 의미한다. 이 모든것을 종합하여 최대 우도법을 정의하면 최대 우도 추정치 또는 최대 가능성 추정량이라고 할 수 있다.


최대우도법은 다음 수식으로 구할 수 있다.
$1.\enspace\theta_{ml}=arg\enspace\underset{\theta}{max}\enspace P_{model}(Y|X;\theta)$
$2.\enspace\theta_{ml}=arg\enspace\underset{\theta}{max}\enspace \displaystyle\sum_{i=1}^mlogP_{model}(Y|X;\theta)$


수식 1과같이 입력 값 $X$와 모델의 파라미터 $\theta$가 주어졌을 때, $Y$가 나타날 확률을 최대화 하는 $\theta$를 찾는것이 최대우도법이다. $X$와$Y$가 고정된 상태에서 모델에 $X$를 넣었을 때 실제값 $Y$에 가장 가까운 $\theta$를 찾는것이 수식이다. 이떄 관측치 $m$개가 모두 서로 독립이라고 가정할 때, 언더플로우를 방지하고자 우도에 로그를 취한다면 최대 우도 추정치 식은 $2$와 같다.

로지스틱 회귀 분석은 다음 절차에 따라 분석을 진행한다.

• 1단계 : 각 집단에 속하는 획률의 추정치를 예측한다. 이때 추정치는 이진 분류의 경우 집단 1에 속하는 확률 $P(Y=1)$로 구한다.
• 2단계 : 분류 기준값(cut-off)을 설정한 후 특정 범주로 분류한다.
  ex ) $P(Y=1)\geq0.5$ -> 집단 1로 분류
  $\enspace \enspace \enspace P(Y=1)<0.5$ -> 집단 0으로 분류

코드를 통해서 살펴보자

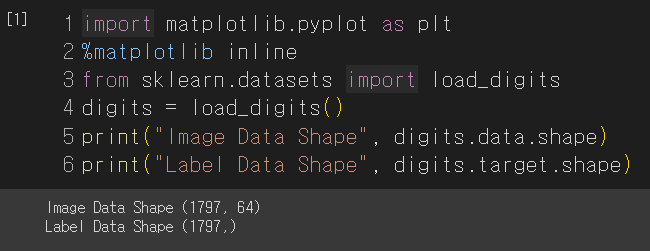
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import load_digits
digits = load_digits()
print("Image Data Shape", digits.data.shape)
print("Label Data Shape", digits.target.shape)

import numpy as np
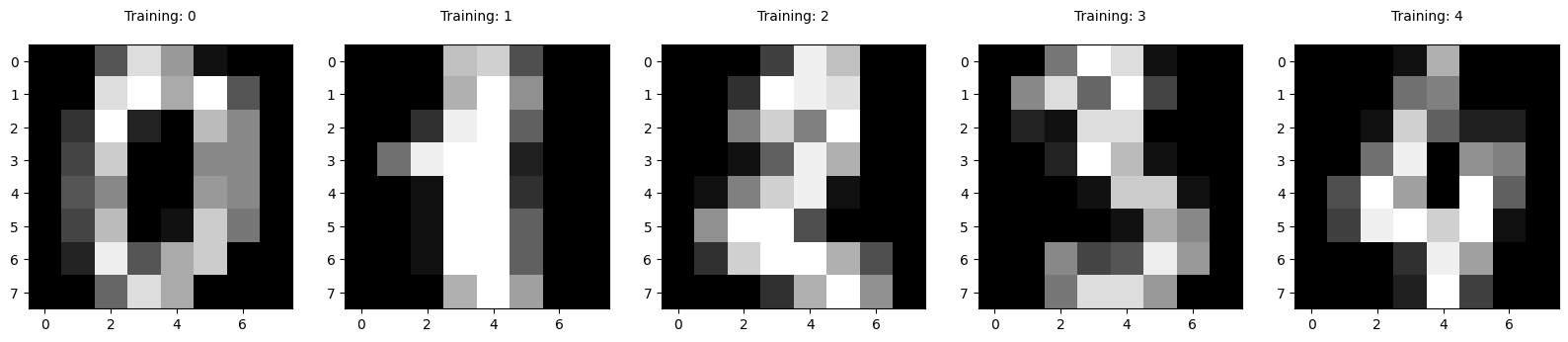
plt.figure(figsize = (20,4))
for index, (image, label) in enumerate(zip(digits.data[0:5], digits.target[0:5])):
    plt.subplot(1,5, index+1)
    plt.imshow(np.reshape(image, (8,8)), cmap = plt.cm.gray)
    plt.title("Training: %i\n" %label, fontsize = 10)
    
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, test_size = 0.25, random_state = 0)

from sklearn.linear_model import LogisticRegression
logisticRegr = LogisticRegression()
logisticRegr.fit(X_train, y_train)

logisticRegr.predict(X_test[0].reshape(1,-1))
logisticRegr.predict(X_test[0:10])

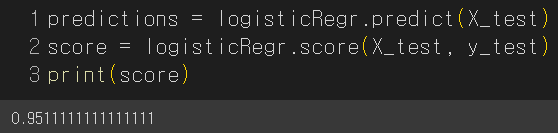
predictions = logisticRegr.predict(X_test)
score = logisticRegr.score(X_test, y_test)
print(score)

import numpy as np
import seaborn as sns
from sklearn import metrics

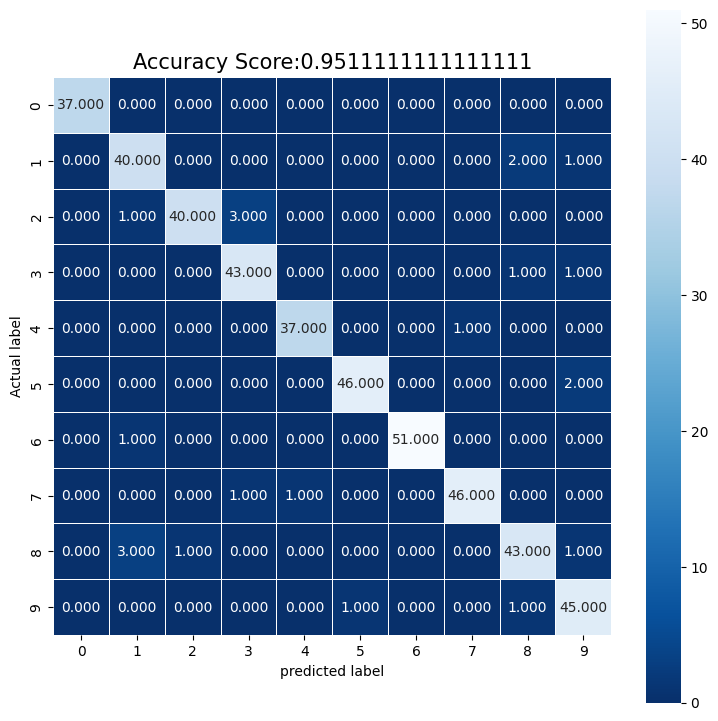
cm = metrics.confusion_matrix(y_test, predictions)
plt.figure(figsize = (9,9))
sns.heatmap(cm, annot = True, fmt = ".3f", linewidths = .5, square = True, cmap = 'Blues_r');
plt.ylabel('Actual label');
plt.xlabel('predicted label');
all_sample_title = 'Accuracy Score:{0}'.format(score)
plt.title(all_sample_title, size = 15);
plt.show();