Network Flow

📝 정의

특정한 지점에서 다른 지점으로 데이터가 얼마나 많이 흐르고 있는가를 측정하는 알고리즘.

네트워크 플로우는 최대 유량문제를 해결하기 위한 알고리즘이다.
그럼 유량이 뭘까?

🛠 특징

교통 체증, 네트워크 데이터 전송 등 다양한 분야에서 활용되고 있다. 예를들어 A 지점에서 C 지점까지 1초에 8개의 데이터를 보내면 B 지점에서는 병목현상이 일어난다. 따라서 A 지점에서는 1초에 3개 씩 전송해야 막힘없이 A 에서 C 까지 막힘없이 데이터를 보낼 수 있다는 것이다.

그리고 이를 보통 유량(Flow)/용량(Capacity) 으로 작성한다.

그럼 A 에서 C 까지 최대한 많은 유량을 보내려고 할 때 가장 합리적인 양은 당연 최소값인 3이다.
이렇게 flow 에 관한 문제를 해결하는 것이다.

⚙ 동작

자, 예를들어 아래와 같은 문제가 있다고 가정할 때, 1 ~ 6 까지 흘려보낼 수 있는 최대 유량을 얼마일까
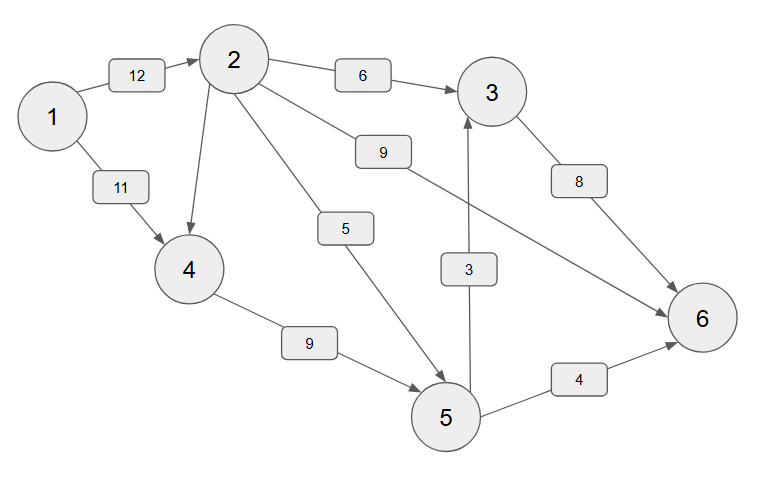이러한 최대 유량 문제는 단순하게 가능한 모든 경우를 탐색하는 방법을 사용하는데 이때, BFS를 이용하는 것이 일반적이다. 이는 에드몬드 카프 알고리즘(Edmons-Karp)이라고도 한다.

1. 우선 각 간선 별 용량을 정해주고 특정 경로에 대하여 계산한 최소 유량을 계속 더해준다.
   예를 들어 1에서 6으로 가는 경로를 계산하면 다음과 같다.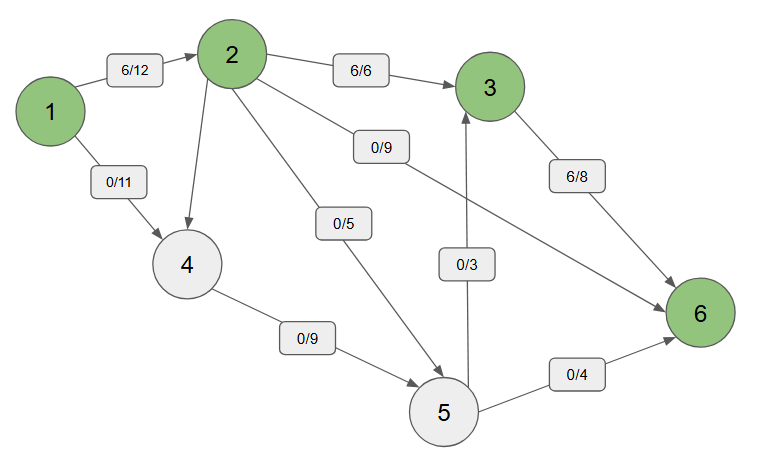

2. 다음 1에서 2를 거쳐 6으로 바로가는 경우는 이제 1->2 의 용량이 6밖에 안 남았으니 6을 더해주고 2->6 의 용량과 비교하여 6이 더 작으니 6만큼 흘려보내 준다.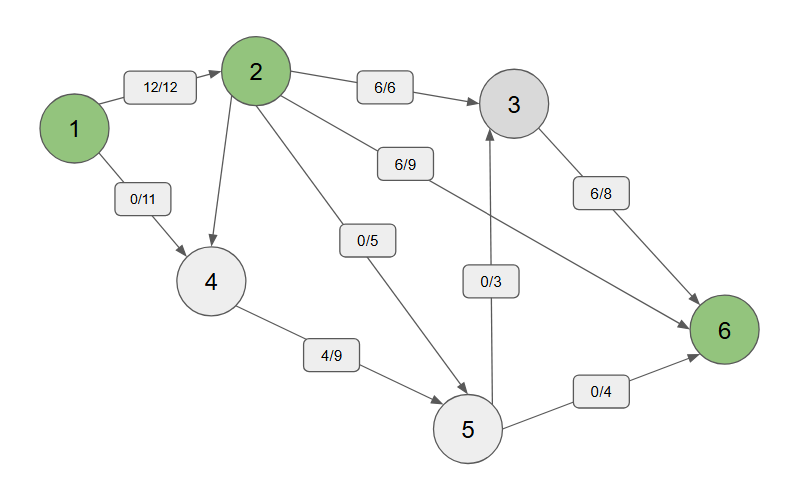

3. 1, 4, 5, 6 경우

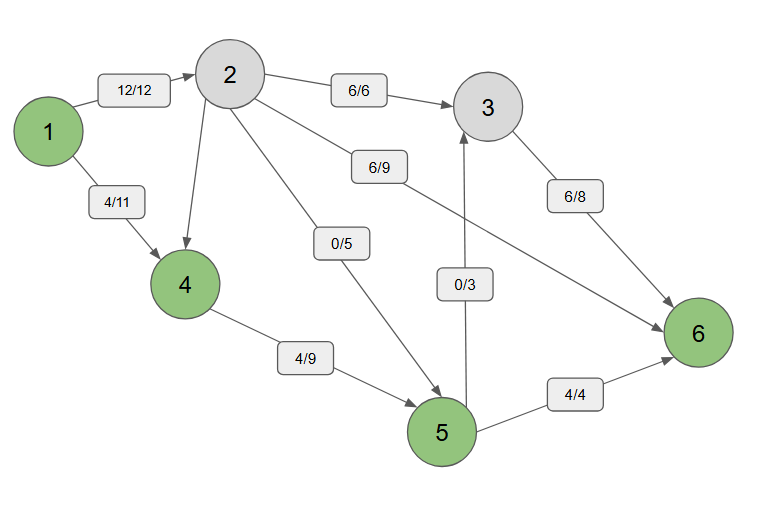
4. 1, 4, 5, 3, 6 의 경우

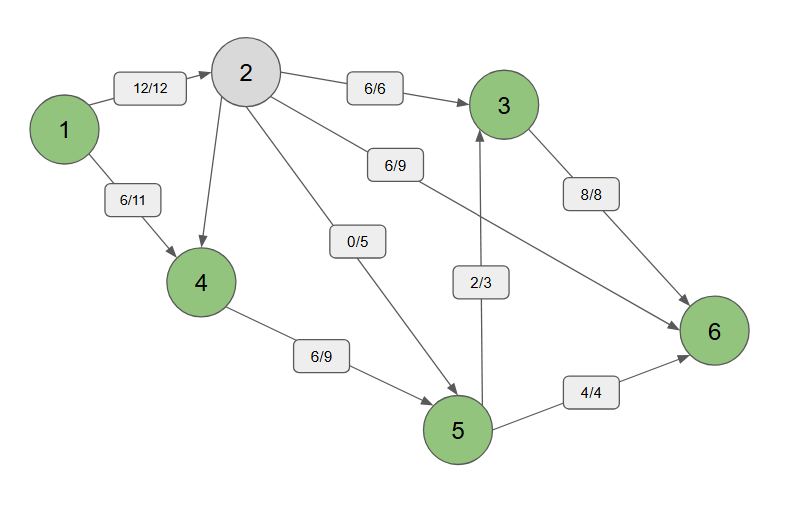
• 자, 그런데 이렇게 보내면 효율적이지 않다. 따라서 우리는 가능한 모든 경로를 다 계산해주기 위해 음의 유량을 계산하여 단순히 유량을 더해주는 과정에서 사실은 보이지 않게 반대로 가는 유량을 빼도록 한다.

예를 들어 2->3 에 음의 유량을 설정하여 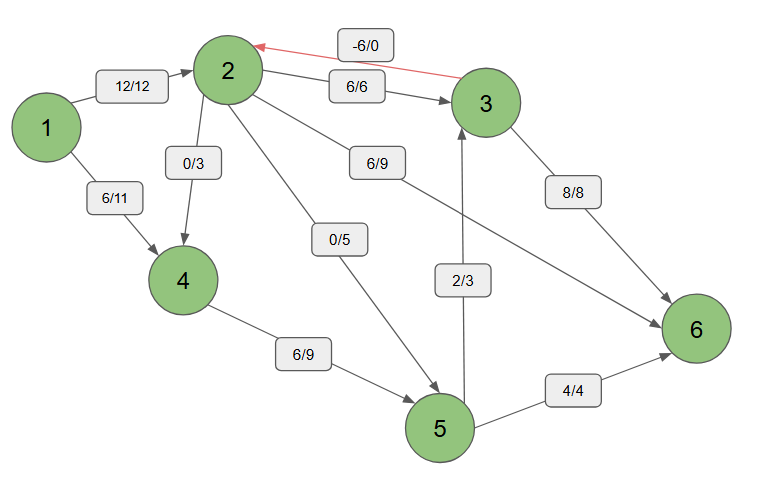1,4,5,3,2,6 의 경로로 설정하면 5->3 경로에 1의 유량을 더 흘려보낼 수 있으니 다음과 같이 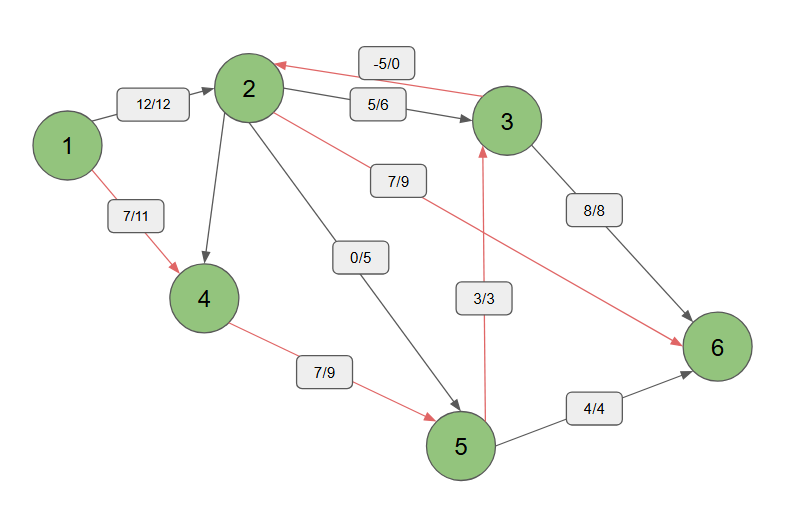그래프가 생성된다. 따라서 정점 1 에서 정점 6 으로 가는 최대 유량을 19(12+7)가 된다.

최대 유량 알고리즘은 순서가 상관없다. 남아있는 양이 1이 넘으면 계속해서 흘려 보내주면 알아서 최적화가 이루어진다는 점에서 특별한 상황이 아니면 유량을 보내는 순서를 고려할 필요가 없다.

⏰시간 복잡도

에드몬드 카프 알고리즘으로 구현할 경우 BFS 로 동작하기에 O(VE^2) 이다.

💻 코드

import java.util.LinkedList;
import java.util.Queue;

public class MaxFlow {

    private static final int INF = Integer.MAX_VALUE;

    // 잔여 그래프에서 증강 경로를 찾기 위한 BFS
    private static boolean bfs(int[][] residualGraph, int source, int sink, int[] parent) {
        int n = residualGraph.length;
        boolean[] visited = new boolean[n];
        Queue<Integer> queue = new LinkedList<>();
        
        queue.add(source);
        visited[source] = true;
        parent[source] = -1;

        while (!queue.isEmpty()) {
            int u = queue.poll();

            for (int v = 0; v < n; v++) {
                if (!visited[v] && residualGraph[u][v] > 0) {
                    queue.add(v);
                    parent[v] = u;
                    visited[v] = true;

                    if (v == sink) {
                        return true;
                    }
                }
            }
        }
        return false;
    }

    // Edmonds-Karp 알고리즘 구현
    public static int edmondsKarp(int[][] graph, int source, int sink) {
        int n = graph.length;
        int[][] residualGraph = new int[n][n];

        // 잔여 그래프 초기화
        for (int u = 0; u < n; u++) {
            for (int v = 0; v < n; v++) {
                residualGraph[u][v] = graph[u][v];
            }
        }

        int[] parent = new int[n];
        int maxFlow = 0;

        // 증강 경로가 있는 동안 흐름을 증가시킴
        while (bfs(residualGraph, source, sink, parent)) {
            // 증강 경로의 최소 잔여 용량 찾기
            int pathFlow = INF;
            for (int v = sink; v != source; v = parent[v]) {
                int u = parent[v];
                pathFlow = Math.min(pathFlow, residualGraph[u][v]);
            }

            // 간선과 역간선의 잔여 용량 업데이트
            for (int v = sink; v != source; v = parent[v]) {
                int u = parent[v];
                residualGraph[u][v] -= pathFlow;
                residualGraph[v][u] += pathFlow;
            }

            maxFlow += pathFlow;
        }

        return maxFlow;
    }

    public static void main(String[] args) {
        int[][] graph = {
                {0, 16, 13, 0, 0, 0},
                {0, 0, 10, 12, 0, 0},
                {0, 4, 0, 0, 14, 0},
                {0, 0, 9, 0, 0, 20},
                {0, 0, 0, 7, 0, 4},
                {0, 0, 0, 0, 0, 0}
        };

        int source = 0;
        int sink = 5;

        System.out.println("최대 유량: " + edmondsKarp(graph, source, sink));
    }
}